The ISO calls for reactive power offers from the reactive power providers. The structure of these offers should ideally reflect their cost of providing reactive power; this issue is dis- cussed in more detail below. Based on the received offers, the
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 125
ISSN 2229-5518
Two Level Structure for Reactive Power in
Deregulated Electricity Markets
Anil Gupta anilrgpv@gmail.com
Abstract— The main objective of this Paper is to propose an two level structure for reactive power in deregulated electricity markets.Considering the various issues associated with the existing policies and practices for reactive power management and payment mechanisms, a competitive two level reactive power management structure is proposed. This structure is based on the separation of reactive power management into two distinct time-frames, i.e. a reactive power procurement stage carried out on a seasonal basis, and a reactive power dispatch stage that determines the reactive power levels in “real-time”.
Index Terms— Reactive power management, Deregulated electricity markets, Reactive power procurement, Reactive power dispatch.
—————————— ——————————
HE Reactive power is tightly related to bus voltages throughout a power network, and hence reactive power services have a significant effect on system security. Insuf- ficient reactive power supply can result in voltage collapse, which has been one of the reasons for some recent major blackouts; for example, the US-Canada Power System Outage Task Force states in its report that insufficient reactive power was an issue in the August 2003 blackout, and has recom- mended strengthening the reactive power and voltage control practices in all North American Electric Reliability Council (NERC) Regions [1]. In deregulated electricity markets, the Independent System Operator (ISO) is responsible for the pro- vision of additional services that are necessary to support the transmission of electrical energy while maintaining secure and reliable operation of the power system; these services are re- ferred to a ancillary services. According to the Federal Energy Regulatory Commission (FERC) Order No.888, reactive power supply and voltage control from generators is one of six ancil- lary services that transmission providers must include in an open access transmission tariff [2]. FERC Order 2003[3] further states that a reactive power provider should not be financially compensated when operating within a power factor range of
0.95 lagging and 0.95 leading, but an Independent System Op-
erator (ISO) may change this range at its discretion. System
operators and researchers have been looking for appropriate
mechanisms for reactive power provision in the context of
deregulation [4],[5],[6],[7].
However, there are several issues concerning the existing pro-
vision policies and payment mechanisms for reactive power
services that impede the full development of a competitive
————————————————
market. Hence, this paper proposes a possible market struc- ture and related techniques to address some of the main issues associated with reactive power provision in competitive elec- tricity markets.
It is well accepted that the principal function of a synchronous generator is to generate real power to meet the demand of the system[8]. Under certain circumstances, usually arising from critical system conditions, the ISO may request or instruct a generator to increase its reactive power output, which may require a reduction in its active power output, thereby affect- ing market conditions.
An important issue that arises with regards to reactive power markets is the choice of an appropriate payment mechanism. Should it be a market-based auction mechanism where the supliers provide their reactive power bids to the ISO, which in turn determines the best reactive power offer using an appro- priate objective function? If so, should it then be a uniform price market for reactive power with a single reactive power price for the whole system, or a zonal level reactive power auction market where the system is divided in zones and sep- arate reactive power prices are determined for each zone?
In a competitive electricity market, reactive power provision by the ISO should be achieved in an optimal manner. The question that arises here is: what is the best optimization crite- rion to be adopted by the ISO? In other words, what is the op- timization objective that the ISO should be seeking to deter- mine the system reactive power schedules? Should it be sys- tem loss minimization, as it has been the usual practice, or minimization of reactive power costs?
It has been the general experience of market operators and
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 126
ISSN 2229-5518
ISOs that energy prices can be highly volatile under certain system conditions, such as demand spikes or outages. In a short-term operational time-frame, volatile energy market conditions would certainly have an impact on reactive power procurement and dispatch procedures.
In a reactive power market, it is certainly possible that some “well-located” suppliers may try to game the price offers by submitting excessively high price offers, or withholding reac- tive power supply in an attempt to increase the reactive power market price to their advantage[9],[10],[11].
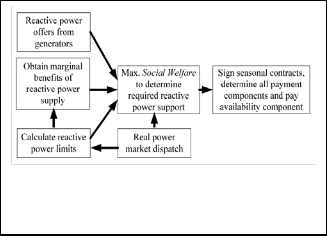
A two-settlement reactive power management scheme is pro- posed here comprising two major activities at different hier- archical levels as depicted in Fig. 1. The first level consists of a long-term procurement market on a seasonal basis. In the se- cond level, the ISO carries out the actual reactive power dis- patch in a time frame of 30 minutes to 1 hour ahead of realtime, by solving an OPF with an appropriate objective function.
As mentioned earlier, the first level in the proposed hierar- chical reactive power management scheme is the design of a procurement market model. The objective of the ISO in this case is essentially to define and procure adequate long-term reactive power supplies for the system. The proposed pro- curement market would work as follows (see Fig. 2):
The ISO calls for reactive power offers from the reactive power providers. The structure of these offers should ideally reflect their cost of providing reactive power; this issue is dis- cussed in more detail below. Based on the received offers, the
Fig : 2 Long term procurement market for reactive power
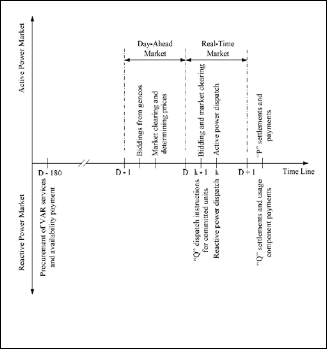
Fig. 1. Active and reactive market clearing and dispatch at day
D and hour K
Figure 1 illustrates how the active and reactive power markets can be decoupled from each other, placing them in different operating time frames, so that the ISO does not handle a reac- tive power auction in the same time frame as that of a real power auction. This minimizes the risk that might arise from price volatility, and thus help reduce market inefficiencies.
ISO carries out an auction settlement, i.e. solves an optimiza- tion model to maximize a societal advantage function (SAF) subject to system constraints that include system security.This procurement market settlement, i.e. the solution of the optimi- zation model, yields a set of contracted generators, as well as the price components of reactive power. The contracted pro- viders will have a seasonal obligation for reactive power pro- vision, and receive an availability payment.
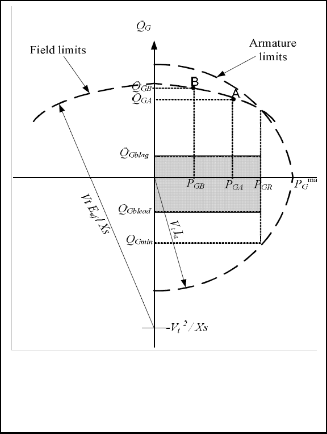
power capability of a generator . These limits are illustrated
in Fig. 3, where Vt is the voltage at the generator terminal bus, Ia is the armature current, Ef is the excitation voltage,XS is the synchronous reactance, and PG and QG are the real and reac-
tive power outputs of the generator, respectively. The genera-
tor’s MVA rating is the point of intersection of the two curves,
and therefore its real power rating is given by PGR . At an op- erating point A, with real power output PGA such that PGA < PGR , the limit on QG is imposed by the generator’s field wind- ing heating limit; whereas, when PGA > PGR , the limit on QG is
imposed by the generator’s armature winding heating limit.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 127
ISSN 2229-5518
vantage Function) which is basically determination of aggre- gate system benefits accrued from reactive power services mi- nus the expected payment by the ISO.
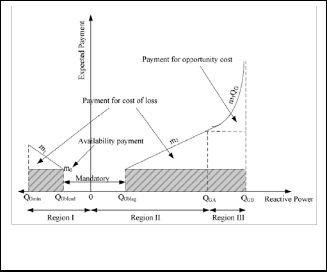
The different reactive power cost components discussed form the basis for the procurement procedure proposed here. Hence, the reactive power price offers to be submitted by gen- erators should comprise the following three parts (Fig. 4) :
Fig : 3 Synchronous generator capability curve
Fig : 4 Reactive power offers from generators and the three operating regions.
Three regions for reactive power generation can be identified in Fig. 3. In Region I (QGmin = QG = Q G1 = 0), the generators are required to mandatorily provide a base leading reactive power support (QGblead to 0). Any reactive power provided beyond QGblead is eligible for an under-excitation payment component as an ancillary service.
In the same way, in Region II (0 = QG = Q G2 = QGA ) , the mandatory lagging reactive power requirement is from0 to QGblag , and any reactive power provision beyond QGblag is rec- ognized as an ancillary service, and thus eligible for a pay- ment for the increased losses in the windings; this payment component is referred to as cost of loss payment The shaded area in Fig. 3 represents the mandatory base reactive power provision range set by the system operator.
In Region III (Q GA = QG = QG3 = Q GB ), any reactive output increase requested by the ISO beyond QGA will require a de-
crease in active power generation, and hence an opportunity
cost payment to the reactive power service providers is ex- pected.
Based on this optimization of reactive power whichgives La- grange multipliers that represent the marginal benefit
/contribution of each reactive source, SAF is maximized. The classical concept of social welfare from economic theory is extended to formulate a reactive power SAF (Societal Ad-
Availability price offer (mo , $): A fixed component to account for that portion of a supplier’s capital cost that can be attribut- ed to reactive power production.
Cost of loss offer (m1 , m2 , $/Mvar): An assumed linearly varying component to account for the increased winding loss-
es as reactive power output increases, in the under and over- excitation ranges respectively [10].
Opportunity offer (m3 , $/Mvar/Mvar): A quadratic com- ponent to account for the lost opportunity cost when a suppli- er is constrained from producing its scheduled real power in order to increase its reactive power production.
Uniform price market , where all selected participants are paid a uniform price, which is the price of the highest accepted of- fer. The uniform price markets provide an incentive to partici- pants to bid their true costs and hence such auctions promote competition. Zonal uniform price mechanism for reactive power markets would reduce the impact of market power ex- ercised by certain gaming generators, and should hence re- strict them only to their given zones.
Once the reactive power ancillary service limits and the mar- ginal benefits of each provider with respect to generation cost are determined, and reactive power offers are received, the ISO is in a position to carry out a procurement market settle-
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 128
ISSN 2229-5518
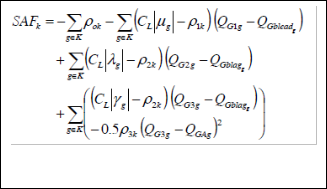
ment where its sole objective is to maximize a societal ad- vantage function The proposed SAF is formulated on a zonal basis and can be expressed as follows: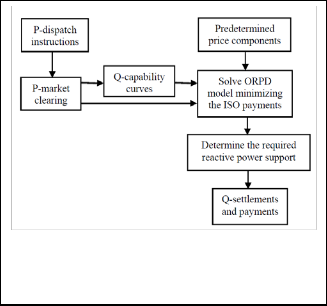
(1)
In (1),the subscript g denotes a generator in the system ,while K refers to the set of generators in zone k,considering that the system is divided into voltage control zones. The variables ρ1k (in $/Mvar) and ρ2k (in $/Mvar) are the under- and over- excitation prices for reactive power in zone k,respectively; similarly ρ3k(in $/Mvar/Mvar) is the zonal uniform oppor- tunity price component .The variable ρok (in $) is the zonal availability price component. The constant CL is a “loadabil- ity” cost parameter (in $/MWh) denoting the economic worth of increasing the system loadability. λ, γ and μ are the La- grange multipliers obtained from optimization model of mar- ginal benefits of reactive power supply with respect to genera- tion cost. QGblag, QGblead are the mandatory lagging and leading reactive power provided by generator. QG1g, QG2g and QG3g are regions of reactive power as shown in fig4.
The proposed schematic procedure is shown in Figure 5 for short term dispatch of reactive power services. In this model, the ISO carries out the reactive power dispatch in a time frame of one hour to half-hour ahead of real-time by solving an OPF that minimizes the cost of reactive power provision from gen- erators, the cost of active power rescheduling, and the cost of real power balance, subject to power flow and security con- straints.
The payments to the service providers are calculated post real-time operation, based on the actual usage and dispatch requested by the ISO aggregated over a period of time.
Fig : 5 Flow Chart for the proposed short term reactive power dispatch model
Reactive power production capability of a generator essential- ly depends on the current state of real power generation (PG ). Hence, prior knowledge of PG is essential in order to calculate reactive capability limits. The values of PG for the generators are obtained from real power market clearing information.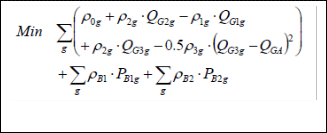
A cost-based Q-dispatch model is proposed here, which takes into account both economic and technical issues associ- ated with reactive power service provisions in a competitive electricity market. The model is formulated as follows: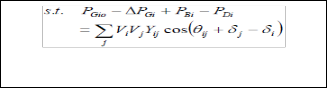
(2)
(3)
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 129
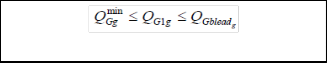
ISSN 2229-5518

(12)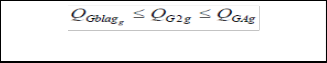
(4)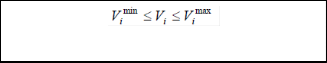
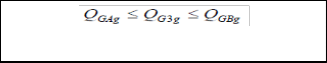
(13)
(5)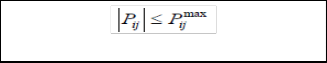
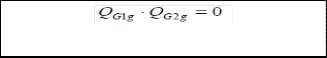
(14)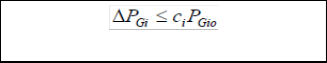
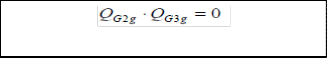
(6)
(15)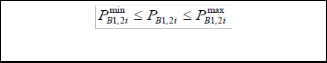
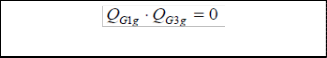
(7)
(16)
(8)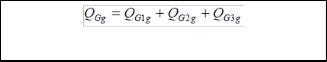
(17)
(18)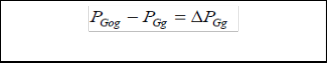
(9)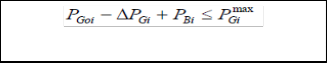
(10)
(11)
where
ρB1 : Price of the upward balance services PB in $/MW.
ρB2 : Price of the downward balance services PB in $/MW.
ρog : Availability price for generator g in $.
ρ1g : Price of Losses in the under-excitation region for gen- erator g in $/MVar.
ρ2g : Price of losses in the over-excitation region for genera- tor g in $/MVar.
ρ3 g : Loss of opportunity price for generator g in
$/MVAr/MVar.
ΔPGi Reduction in active power at bus i due to increase in reactive power beyond heating limits.
PGoi : Pre-determined active power dispatch at bus i. PBi1 : Upward balance service at bus i.
PBi2 : Downward balance service at bus i.
ci : Maximum allowed level of active power reduction at bus i.
PG x g : New active power dispatch for generator g.
The proposed reactive power dispatch model is supposed to run in a 30 min to 1 h window, and the solution yields the required reactive power support that minimizes the payment
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 130
ISSN 2229-5518
by the ISO, while considering system security constraints rep- resented through voltage limits (5) and transmission line pow- er flow limits (6).
Based on the current practices for reactive power provision by various ISOs in competitive electricity markets, this paper has proposed a streamline reactive power market structure. The proposed market design consists two stages, namely, pro- curement of reactive power resources on a seasonal basis, and a real-time reactive power dispatch. The proposed procure- ment market model, which is the main focus of this paper, is based on at first level with two-step optimization process; the first step consists of the determination of the marginal benefits of reactive power with respect to generation cost, which are then used in the second step to maximize a reactive power societal advantage function (SAF) considering bids from ser- vice providers. In the second level, reactive power dispatch which is basically short term management is considered based on first result.
[1] US-Canada Power System Outage Task Force, Final Report on the August 14,
2003 Blackout in the United States and Canada: Causes and Recommenda- tions, Issued April 2004.
[2] FERC Order No.888, “Promotion of wholesale competition through open access non-discriminatory transmission services by public utilities and recov- ery of stranded costs by public utilities and transmitting utilities,” Issued April
1996.
[3] FERC Order No.2003, “Standardization of general interconnection agree- ments and procedures,” Issued Aug. 2003.
[4] New York Independent System Operator Ancillary Services Manual, 1999.
[5] National Electricity Market Management Company (Australia), “National electricity market ancillary services,” Nov. 1999.
[6] FERC Staff Report, “Principles for efficient and reliable reactive power supply and consumption,” Feb. 2005.
[7] J. Zhong and K. Bhattacharya, “Reactive power management in deregulated
power systems- A review,” Proceedings of the IEEE Power Engineering Society
Winter Meeting, vol. 2, pp. 1287-1292, 2002.
[8] E. Fitzgerald, C. Kingsley Jr. and S. D. Umans, Electric Machinery, McGraw- Hill, 1992.
[9] FERC Order No.2000, “Regional transmission organizations,” Issued Dec.
1999.
[10] F. M. Schere, Industrial Market Structure and Economic Performance, Rand
McNally and Company, 1970.
[11] A. F. Rahimi, and A. Y. Sheffrin, “Effective market monitoring in deregulated electricity markets,” IEEE Trans. Power Syst., pp. 486-493, May 2003.
IJSER © 2013 http://www.ijser.org