International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 1
ISSN 2229-5518
Traffic based Virtual Topology Design in a Small WDM Network with Comparative Analysis of Wavelength Dependent Cost of Established Lightpaths
Ms. Harmandar Kaur
—————————— ——————————
he virtual topology design is performed with the aim of optimizing the network parameters in such a way so as to improve the networks overall performance. The
objective functions which are commonly considered are either optimizing number of wavelengths required to establish a given set of lightpaths, or to establish as many lightpaths as possible for a given set of wavelengths; or to establish lightpaths for a given set of wavelengths to maximize the total traffic throughput of the given network.[1][2][7][8]
Herein we have the objective of establishing lightpaths offering maximum traffic load satisfaction with a wavelength-dependant least cost path. The assumption made is that the traffic offered to a lightpath is independent of that offered to the others.
The constraints like the virtual degree constraint and the wavelength conflicting constraint are useful to help design a close to practically realizable virtual topology. The virtual degree constraint limits the number of lightpaths originating or terminating at a given node, by setting them less than or equal to the number of transmitters or receivers present with a node.
————————————————
Ms.Harmandar Kaur is currently working as assistant professor at Lovely
ProfessionalUuniversity,Punjab,India E-mail: harmandar_09@yahoo.co.in
Hence, the value of virtual degree constraint throughout the network remains same, for reducing computational complexity.The wavelength conflicting constraint ensures that no two or more lightpaths are capable of sharing same wavelength on a physical link. The establishment of a virtual topology is dependent on how properly the transmitters, receivers, wavelengths and traffic requests are utilized. In the given physical topology, there exist bidirectional links between the connected node pairs, i.e. say the wavelength constraint is set to 2, which imply that a link is capable of supporting two wavelengths between a given node pair by having two channels or two fibres multiplexed on the same fibre. [2]
The traffic inputs to four and six node networks are different and completely random in nature. The design of the virtual topologies is done considering the traffic.
A virtual topology is created over a given physical topology consisting of weighted links, taking into account some important parameters. The parameters like physical links, traffic, distance are input to the design algorithm in the form of matrices, with nxn dimensions, where n denotes the number of nodes in the topology[5]. Considering the given physical topology as the base[10], a virtual topology is designed, taking into consideration the virtual degree (vd) and the wavelength constraints.
(i)Traffic Dependant Algorithm
IJSER © 2011
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 2
ISSN 2229-5518
The Decreasing Traffic Sequence (DTS) virtual topology design algorithm is aimed at reducing the network load by giving priority to the highest traffic demand. This procedure is followed to minimize large traffic build-ups and hence congestion and propagation delay. The steps for the DTS-VTD algorithm is carried out by arranging the traffic flows in the traffic matrix are sorted in descending order; the highest traffic flow is assigned light path in accordance with the wavelength and vd constraints. The small WDM network, consisting of four to six nodes[4], would adopt different virtual topologies depending on the virtual degree supported. The weights on the links between the nodes are the distances between them.
Table1. Virtual Topology Design for Dts-Vtd Algorithm with vd=1.
![]()
![]()
The topology designed with a four node network with one transceiver, is established in accordance with the vd and the wavelength constraints. Due to the violation of the vd constraint, the links from iterations 4 to 9 have not been established, though they stand first in the order of the traffic amount. The links in this case are not considered as the bidirectional ones, i.e. the wavelength constraint has a value equal to 1 here.As the value for virtual degree is increased, more lightpaths can be build. With a vd value equal to 2, more traffic demand can be sorted. The design of lightpath topology is different for different values of the virtual degree constraint. In this design a hop is incorporated in the fourth iteration, in order to meet the aim of the DTS algorithm. Here again the wavelength constraint is unity. Taking wavelength constraint
Table2. Virtual Topology Design for Dts-Vtd Algorithm with vd=2.
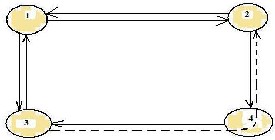
Fig.1. Lightpath topology for DTS-VTD with vd=2
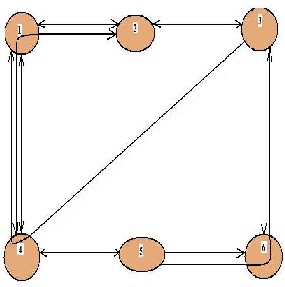
as unity means no bidirectionality in links.though the lightpath topology looks the same, it actually consists of two counter clockwise flowing topologies forming a sort of dual ring structure.The virtual topology can be depicted by using ones to signify a virtual connection between nodes, and a zero for no virtual link. For a virtual degree 3 value the virtual topology designed can be represented as:
VT: 0111 1011 1101 1110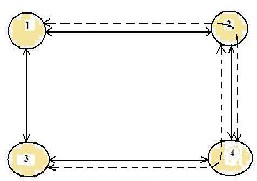
Fig.2. Lightpath topology for DTS-VTD with vd=3
Also the wavelength constraint is taken as 2, Depicted by double arrowheaded link.
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 3
ISSN 2229-5518
11.2
11
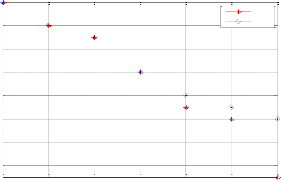
Fig.4. Virtual topology Design with DTS-VTD for vd=3, showing the link length between nodes(in kms)
10.8
10.6
10.4
10.2
10
9.8
9.6
1 2
via node2 via node4
3 4
In the figure 7, the actual light path connectivity between the nodes is shown. The links are capable of handling one wavelength per fiber, hence both the lightpaths i.e. 1->2->3-
>4->5->6->1 and 1->6->5->4->3->2->1 exist on two separate fibres. For the same case, considering the value of wavelength constraint to be 2, a totally different virtual
topology is obtained which has hops in it.
9.5 10 10.5 11 11.5 12 12.5
Fig.3. Virtual topology Design with DTS-VTD for vd=3,showing the link length between nodes(in kms)
Table3. Virtual Topology Design for Dts-Vtd Algorithm with vd=3.
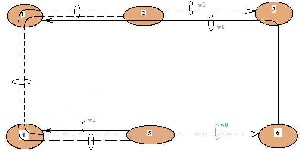
Fig.5. Lightpath topology for DTS-VTD with vd=2,M=2,maximum hops=4
This is realizable when the link is able to handle two wavelengths per fiber. The maximum hop length consisting of four hops is needed to channelize the traffic. A limit can be imposed on the maximum number of hops between the node pairs, using a virtual hop matrix.[6]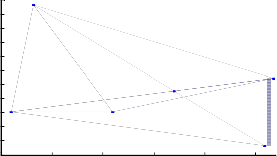
16
2
15
14
13
12
11
4
In this case, hops are present and are possible via 10
intermediate node 2 and 4. This node performs the opto- 9
electronic and electro-optical routing. [2] In vd=3, all the 8 1 6
traffic demands arising are satisfied. Now, if a six-node
6
network is considered, new physical link, traffic and 5
5
distance matrices are taken. With virtual degree value
equal to 2, and taking the value of wavelength constraint as
1, which means a link is capable of supporting only one
wavelength between a node pair. The virtual topology is
simple and is given as:
VT: 0 1 0 0 0 1;1 0 1 0 0 0;0 1 0 1 0 0;0 0 1 0 1 0;0 0 0 1 0 1;1 0 0
0 1 0
DTS-VTD VD=2 NODES=6
0 5 10 15 20 25
Fig.6. Virtual topology Design with DTS-VTD for vd=3, showing the link length between nodes(in kms)
The realised virtual topology can be considered for cost effectiveness by the Joint Wavelength Routing (JWR) Algorithm. Lightpaths have an important role in the cost effective management of network resources [9].The algorithm is applicable to the node pairs with two or more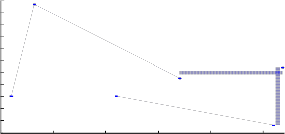
16
2 than two lightpaths between the nodes.
14
13
12
11
4
10
3
9
8 1 6
7
6
5
5
0 5 10 15 20 25
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, No 4
ISSN 2229-5518
Fig.9. Lightpath topology for DTS-VTD with vd=3,M=2]
DTS-VTD VD=3 NODES=6
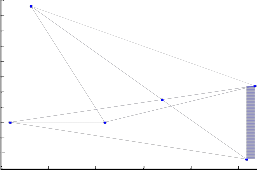
16
2
15
14
13
12
Fig.7. Lightpath topology for DTS-VTD with vd=2,M=2
DTS-VTD VD=2 NODES=6
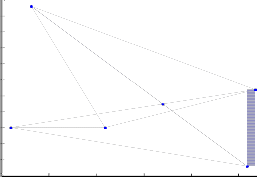
16
2
15
11
4
10
3
9
8 1 6
7
6
5
5
14
13
12
11
4
10
3
9
8 1 6
7
6
5
5
0 5 10 15 20 25
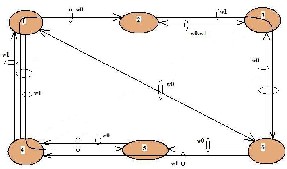
Fig.10. Virtual topology Design with DTS-VTD for vd=3, showing the link length between nodes(in kms)
The routes depicted in the figure 14, are R0: 1->5,R2:1-
>4,R4:4->2,R6:3->5,R7:4->6 depending on the wavelength
used there is a variation in the cost associated.
cost parameter
12
0 5 10 15 20 25
Fig.8. Virtual topology Design with DTS-VTD for vd=2, showing the link length between nodes(in kms)
The parameters needed to search for the wavelength dependant least cost lightpath are:
A(wi): number of links on which wavelength wi exists
L(Rpj):denotes the hop length
F(Rpj):denotes the free wavelengths on Rpj
C(wi, Rpj)=α1. A(wi)+(1- α1){ α2[w- F(Rpj)]+( 1- α2). L(Rpj)}
where α1 and α2 are variables such that α1>=0 and α2>=1.[3] Every lightpath has a particular wavelength associated
with it.
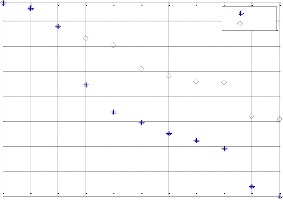
For DTS with vd=3, the complexity in wavelength assignment and hop length increases.
c1:C(w1,Rp0)
11 c2:C(w2,Rp0)
10 c5:C(w1,Rp2)
c6:C(w2,Rp2)
9 c9:C(w0,Rp4)
c10:C(w1,Rp4)
8 c11:C(w2,Rp4)
c15:C(w1,Rp6)
7 c16:C(w0,Rp7)
6
5
4
3
2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
alpha1
Fig. 11. Wavelength dependant cost of lightpaths in DTS-VTD with vd=3,M=2.
(ii). Traffic Independent Algorithm
Another algorithm doesn’t take into consideration the traffic, hence the name Traffic Independent (TI) Algorithm. For a four node network, with different vd values, it establishes all possible lightpaths. VT: 0100 0001 1000 0010;
0010 1000 0001 0100
Lightpaths: 1--2--4--3--1 via W0; 1--3--4--2--
1 via W1
In case the virtual degree value is 2,then:
VT 0110 1001 1001 0110
RWA 1--2--4--3--1 and 1--3--4--2--1 via W0
In case the virtual degree value is 3,then:
VT 0111 1011 1101 1110
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 5
ISSN 2229-5518
RWA VD=2 case plus 1--4, 4--1 via W1; 2--3, 3--2 via W1
Fig.12. Lightpath topology for TI-VTD with vd=3,M=2
Fig.14. Virtual topology Design with TI-VTD for vd=2, showing the link length between nodes(in kms)
VT:[0 1 1 1 0 0;1 0 1 1 0 0;1 1 0 0 0 1;1 1 0 0 1 0;0 0 1 1 0 1;0 0 0
0 0 0]
This is the virtual topology configuration for vd value 3. The routes depicted in the figure 21, are R0: 2->4,R1:4-
>2,R2:3->1,R3:5->3 depending on the wavelength used there is a variation in the cost associated.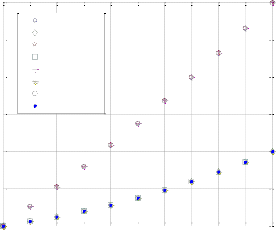
8
c1:C(w0,Rp0))
c2:C(w1,Rp0)
7 c3:C(w0,Rp1) c4:C(w2,Rp1) c5:C(w0,Rp2)
6 c6:C(w1,Rp2)
c7:C(w0,Rp3)
c8:C(w2,Rp3)
5
cost parameter
c1=c3=c5=c7
4
3
c2=c4=c6=c8
Fig.15. Lightpath topology for TI-VTD with vd=3,M=2
2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
alpha1 9
cost parameter
Fig. 13. Wavelength dependant cost of lightpaths in TI-VTD with vd=3,M=2.
The routes depicted in the figure 17, are R0: 4->1,R1:2-
>3,R2:1->4,R3:3->2 depending on the wavelength used there
is a variation in the cost associated.
For a six node network, taking M=1, ie each fiber link supports single wavelength value, the vd 2 virtual topology is:
VT:[0 1 0 1 0 0;1 0 1 0 0 0;0 1 0 0 0 1;1 0 0 0 1 0;0 0 0 1 0 1;0 0 1
0 1 0]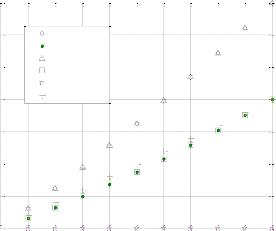
8 c1:C(w0,Rp0)
c2:C(w1,Rp0)
c3:C(w0,Rp1)
7 c4:C(w1,Rp1)
c5:C(w2,Rp2)
6 c6:C(w1,Rp3)
5
4
3
TI-VTD VD=2 NODES=6
16
2
15
14
2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
alpha1
13
12
11
10
3
9
8 1 6
7
Fig. 16. Wavelength dependant cost of lightpaths in TI-VTD with
4 vd=3,M=2.
6
5
5
0 5 10 15 20 25
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 6
ISSN 2229-5518
The virtual topologies designed by the algorithms already discussed can be analysed based on their network load reducing capability. The traffic requests entering a network must be entertained in such a way so as to prevent congestion and delay from occuring. Thus the traffic can be handled as it comes, which is applied with the help of TI-
entertained in the second iterartion in DTS whereas in TI it gets satisfied in the last iteration.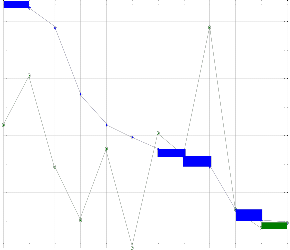
dts vs ti;vd2;nodes6
0.9
DTS
VTD algorithm or it can be dealt with based upon its bulkiness , which is applied with the help of DTS-VTD algorithm. Both these approaches are equally relevant. TI- VTD algorithm is computationally fast as it need not look for the highest traffic demand through out the network, whereas DTS-VTD helps get rid of large traffic demands first leading to lower risk of network congestion.
0.8
0.7
0.6
0.5
TI
DTS TI
0.9
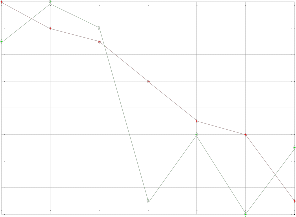
dts vs ti;vd2;nodes4
0.4
TI
0.8
0.3
0.7
DTS
0.2
0.6
1 2 3 4 5 6 7 8 9 10 11 12 iterations
0.5
0.4
Fig. 19. Traffic Demand satisfied versus Iterations for DTS and TI;
vd=2; nodes=6.
0.3
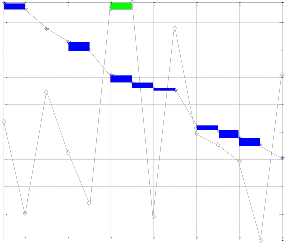
dts vs ti;vd3;nodes6
0.2
0.1
1 2 3 4 5 6 7 iterations
0.9
0.8
TI DTS
Fig. 17. Traffic Demand satisfied versus Iterations for DTS and TI;
vd=2; nodes=4.
0.7
0.6
1
0.9
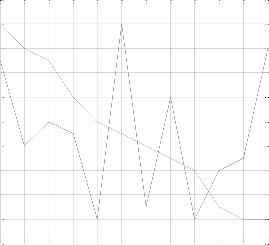
dts vs ti;vd3;nodes4
0.5
0.4
0.8
0.3
0.7
0.6
0.5
DTS
TI
0.2
2 4 6 8 10 12 14 iterations
0.4
0.3
0.2
0.1
0
1 2 3 4 5 6 7 8 9 10 11 12 iterations
Fig. 20. Traffic Demand satisfied versus Iterations for DTS and TI;
vd=3; nodes=6.
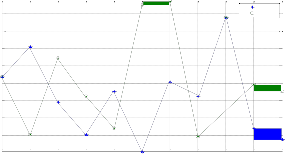
Similar outcomes hold when number of nodes in the network are increased to six. The network load reduction is related to the networks virtual degree value in DTS algorithm and is totally independent in TI algorithm. This holds true even when the number of nodes is increased to six, in a small scale WDM network.
Fig. 18. Traffic Demand satisfied versus Iterations for DTS and TI;
vd=3; nodes=4.
DTS algorithm lowers the network traffic load considerably for the same number of iterations as compared to TI algorithm. The slope varies abruptly in the TI algorithm. The second highest traffic demand value of 0.8 that is
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 7
ISSN 2229-5518
DTS vd2 vs DTS vd3;nodes4
TI vd2 vs TI vd3;nodes6
0.8
vd=2
vd=3
0.9
0.8
vd=2 vd=3
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
1 2 3 4 5 6 7 8 9 10 11 iterations
1 2 3 4 5 6 7 iterations
Fig.
Fig. 24. Traffic Demand satisfied versus Iterations for TI; when vd is
21. Traffic Demand satisfied versus Iterations for DTS; when vd is varied; nodes=4.
TI vd2 vs TI vd3;nodes4
varied; nodes=6.
The cost effectiveness of the lightpaths established via varying the virtual degree and the number of nodes can be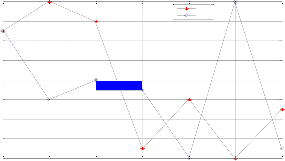
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
vd=2 vd=3
1 2 3 4 5 6 7
used to analyse the best possible lightpaths. All the wavelength dependant least cost lightpaths from different nodes and virtual degree values of the two algorithms are used for the comparitive analysis. There is a comparative increase in the cost of the lightpaths with higher value of the virtual degree constraint. The cost is wavelength dependant, hence there is a direct relation between the number of wavelengths utilised and the virtual degree value.
For the same number of nodes and virtual degree value, the
iterations
Fig. 22. Traffic Demand satisfied versus Iterations for TI; when vd is varied; nodes=4.
DTS vd2 vs DTS vd3;nodes6
vd=2
cost for DTS algorithm is slightly higher than the TI algorithm, which can be compromised with the better traffic handling capability of DTS algorithm. Another observation shows that the cost can be equalised by creating an inverse relation between the number of nodes and the virtual degree value. The wavelength dependant
0.9
0.8
0.7
vd=3
cost for DTS with six nodes and virtual degree value 2 is
the same as that of TI algorithm with four nodes and virtual
degree value 3, hence crecoasttipnagramaenterinverse relation.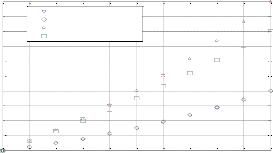
7
c1:TI VD3 NODES4
0.6
0.5
6.5
6
5.5
5
c2:DTS VD2 NODES6 c3:DTS VD3 NODES6 c4:TI VD3 NODES6
0.4
4.5
4
0.3
3.5
1 2 3 4 5 6 7 8 9 10 11 iterations
Fig. 23. Traffic Demand satisfied versus Iterations for DTS; when vd is varied; nodes=6.
3
2.5
2
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 alpha1
Fig.25. Cost versus alpha1 for different values of vd constraint and number of nodes for DTS,TI algorithms.
In this paper, we have designed virtual topologies for a given physical topology, for a small WDM network containing four to six nodes, by varying the virtual degree constraint. Two approaches are adopted : traffic dependent
International Journal of Scientific & Engineering Research, Volume 2, Issue 11, November-2011 8
ISSN 2229-5518
and traffic independent approach. These are analysed by the wavelength dependent cost effectiveness of the established individual lightpaths. By this analysis, lightpaths relation to the number of nodes and virtual degree is made, taking wavelength dependant cost as the parameter.
[1]. Subruta Bunerjee, Jay Yoo, “Minimizing Maximum Logical Link
Congestion in Packet Switched Optical Networks,” IEEE,pp.1298-
1302,1997.
[2]. Biswanath Mukherjee, Dhritiman Banerjee, S. Ramamurthy,and Amarnath Mukherjee, “Some Principles for Designing a Wide-Area WDM Optical Network,” IEEE/ACM Transactions On Networking, vol.
4, no. 5, pp.684-696, October 1996 .
[3]. S.R. Murthy, M.Guruswamy, “WDM Optical Networks: Concepts, Design and Algorithms,” Prentice Hall of India Pvt. Ltd.,New Delhi,2002.
[4]. Biswanath Mukherjee, “WDM-based Local Lightwave Networks
Part I: Single-Hop Systems,”IEEE Network,pp.12-27,May 1992.
[5]. Dhritiman Banerjee, Biswanath Mukherjee “Wavelength-Routed Optical Networks: Linear Formulation, Resource Budgeting Tradeoffs, and a Reconfiguration Study,”IEEE,pp.-276,1997
[6]. R. M. Krishnaswamy and K. N. Sivarajan, “Design of Logical Topologies: A Linear Formulation for Wavelength-Routed Optical Networks with No Wavelength Changers", IEEE/ACM Trans. Networking, vol. 9, no. 2, pp. 186-198, Apr 2001.
[7]. R. Ramaswami and K. N. Sivarajan, “Optimal Routing and Wavelength Assignment in All-Optical Networks", Proc. IEEE Infocom'94, pp. 970-979, Toronto, Canada, Jun 1994.
[8]. S. Banerjee and C. Chen, “Design of Wavelength-Routed Optical
Networks for Circuit Switched Traffic", Proc. IEEE Globecom'96, pp.
306-310, London, UK, Nov 1996.
[9]. J. Burgin and D. Dorman, “Broadband ISDN Resource Management: The Role of Virtual Paths", IEEE Communications Magazine, vol. 29, no. 9, pp. 44-48, Sep 1991.
[10]. O. Komolafe, D. Hale and D. Cotter, “Impact of Graph Theoretic Network Parameters on the Design of Regular Virtual Topologies for Optical Packet Switching", IEEE ICC'02, pp. 2827-2831, New York, Apr
2002.
[11]. Yu Yiding, “Virtual Topology Design for Optical WDM Networks
,” ME Thesis, National University of Singapore,2003