International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 198
ISSN 2229-5518
Thermophoretic Effect on Double Diffusive Convective Flow of a Chemically Reacting Fluid over a Rotating Cone in Porous Medium
S. Hariprasad Raju1, B. Mallikarjuna2* and S.V.K. Varma1
Abstract—In this paper, we analyzed buoyancy driven convective heat and mass transfer flow of a chemically reacting fluid over a rotating cone in porous medium with thermophoretic particle deposition. Darcy law is used to describe the fluid flow in porous medium. The governing equations for mass, momentum, energy and concentration equations are transformed into non-dimensional nonlinear ordinary differential equations using specified similarity transformations and then solved by employing shooting method with 4th Runge-Kutta method. The numerical results are reported graphically for various physical parameters, namely chemical reaction parameter, thermophoretic constant and thermophoresis parameter on tangential, circumferential and normal velocity profiles as well as tangential and azimuthal skin-friction coefficient and rate of heat and mass transfer and thermophoretic particle deposition velocity near the cone surface.
Index Terms: Rotating Cone, Porous Medium, Thermophoresis, Chemical Reaction.
—————————— ——————————
1 INTRODUCTION
The study of combined heat and mass transfer problems has great importance in extending theory of separation processes, chemical and hydro-metallurgical industries. Heat transfer phenomenon in addition to the mass transfer has received great attention of modern researchers for its enormous applications in chemical industries, reservoir engineering and other processes. A few representation fields of this type of flows in which combined heat and mass transfer with chemical reaction effect plays an important role, are electrical energy is extracted directly from a moving conducting fluid, formation and dispersion of fog, damage of crops due to freezing, distribution of temperature and moisture over groves of fruit trees, manufacturing of ceramics, polymer production.
Combined heat and mass transfer in rotating
systems problems are of importance in many processes.
These processes take place in many industrial, geothermal
and engineering applications, such as nuclear plants, vortex
chambers, filtration, shielding of a rotating bodies, design of rotating machinery, oceanic circulations, gas turbines, various propulsion devices for space vehicles, missiles, satellites and aircraft, the design of turbines and turbo machines, in estimating the flight path of rotating wheels and spin-stabilized missiles and in the modeling of many geophysical vortices. At first, Tien [1] analyzed free convective heat transfer from a rotating cone. Hering and Grosh [2] studied in mixed convection and reported the results by dividing the regimes of flow as purely free, forced and combined convection flows. Himasekhar and Sarma [3] analyzed convective heat transfer flow over a rotating cone with suction effect. Chamkha [4] used Darcy’s
————————————————
• S. Hariprasad Raju is currently pursuing Ph.D degree in Sri Venkateswara University, Tirupati, India. E- mail:hariprasadraju@gmail.com
• B. Mallikarjuna, Assistant Professor in BMS College of Engineering,
Bangalore, Karnataka-560019, E-mail: mallikarjuna.jntua@gmail.com
* Corresponding Author: E-mail: mallikarjuna.jntua@gmail.com
• S.V.K. Varma, Professor in Mathematics, Sri Venkateswara University,
Tirupati, India.
model to study convective heat transfer flow past a rotating cone with heat generation and magnetic effect. Recently, Anilkumar and Roy [5, 6] investigated unsteady mixed convection from a rotating cone in a rotating fluid. Unsteady MHD convective flow in the stagnation region of a rotating sphere at constant wall temperature and heat flux conditions is investigated by Chamkha et.al [7]. Chamkha and Rashad [8] studied Chemical reaction and cross diffusion effects on unsteady convective flow over a rotating cone.
Thermophoresis is the migration of aerosol and
other particles in the direction of a reduction of the
temperature gradient. Such a phenomenon encountered in
the engineering applications in aerosol reactors, heat exchanger fouling, optical fiber production etc. In optical fiber synthesis, thermophoresis is identified as the mass transfer mechanism as used in the modified chemical vapor deposition (MCVD). Chamkha [9, 10] studied thermophoretic effect on hydromagnetic convective flow over a flat surface, vertical cylinder, in a fluid saturated porous medium. Partha [11, 12] analyzed thermophoresis particle deposition on natural convective in a non-Darcy porous medium with Soret and Dufour effects under permeable and impermeable conditions. Rahman and Postelnicu [13] investigated thermophoresis effect on forced convective flow of a viscous fluid due to rotating disk. Bakier and Gorla [14] studied thermal radiation effect on convective flow over a semi-infinite vertical plate with thermophoretic effect. Muhaimin et.al [15] investigated impact of thermophoretic particle deposition on unsteady convective flow over a porous wedge in non-Darcy porous medium with chemical reaction and temperature- dependent viscosity. Recently, Kameswaran et.al [16] studied non-linear convection and thermophoresis on convective boundary layer flow over a vertical wall in a non-Darcy porous medium. Bhuvanavijaya and Mallikarjuna [17] investigated the effects of variable properties and thermophoretic on convective heat and mass
IJSER © 2015
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 199
ISSN 2229-5518
transfer flow over vertical wavy surface in a fluid saturated porous medium.
In view of the above applications, authors envisage to investigate thermophoresis particle deposition on buoyancy driven mixed convective heat and mass transfer flow over an impermeable vertical rotating cone in a fluid saturated porous medium with chemical reaction. The following strategy is pursued in the rest of the paper. The problem is formulated in section-2. Section-3 contains the numerical solution. Results and discussions are presented in section-4. The concluding remarks are given in section-5.
dynamic viscosity, g is the acceleration due to gravity, βT
and βC are the thermal and concentration coefficients, α is
the cone apex half angle, K is the permeability of the porous medium, ke is the effective thermal conductivity, c p specific heat at constant pressure, Q is the radiation absorption coefficient and D is the molecular diffusivity, kr is the chemical reaction parameter and r is the radius of the cone.
Following Chamkha [18-19] and Partha [12] and
2 FORMULATION OF THE PROBLEM
We consider the steady boundary layer flow of
Kameswaran et.al [16] thermophoretic velocity vt
written as
v = −k υ ∂T
can be
(7)
axisymmetric, incompressible chemically reacting fluid past
an infinite rotating vertical cone in a fluid saturated porous
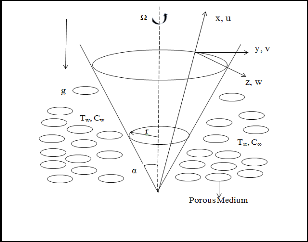
medium. Fig-1 shows physical configuration and
coordinate of the system. Let the vertical cone is assumed to
have variable temperature and variable concentration
which are higher than free stream temperature and

t T ∂z
where k is the thermophoretic constant, T is the temperature.
Introducing the following non-dimensional variables to get the non-dimensional governing equations
Ω sin(α ) 1/ 2
concentration. Consider the rectangular curvilinear

η =
υ
z, u = xΩ sin(α )F (η ), v = xΩ sin(α )G(η ), r = x sin(α )
(8)
coordinate system. Let
u, v and w be tangential (x),


w = (υΩ sin(α ))1/ 2 H (η ), θ (η ) = T − T∞ , φ (η ) = C − C∞
Tw − T∞
Cw − C∞
circumferential (y) and normal velocities (z) respectively.
The fluid saturated porous medium is assumed to be
Tw ( x) − T∞ =
(TL − T∞ ) x
L
, Cw ( x) − C∞ =
(CL − C∞ ) x
L
homogeneous and isotropic which is in locally
where L being the cone slant height and TL
being the cone
thermodynamic equilibrium with solid matrix. The
surface temperature and CL
being the cone surface
physical properties of the fluid are assumed to be constant
except density in the buoyancy force term. The buoyancy force is made up of two components; the fluid temperature and concentration variations. In addition thermal absorption is assumed in energy equation. Using the above assumptions and boundary layer approximations, the governing equations, continuity, Darcy equation (using linear Boussinesq approximation and after eliminating pressure), energy and concentration equation can be
concentration at the base(x=L)
Using (7) and (8), eqns. (1)-(6) reduced into

F = − 1 H ′
2
(9)
2

−H ′′′ + HH ′ − + Da H ′ + 2G + 2g (θ + Nφ ) = 0
2
G′′ − HG′ + H ′G − Da−1G = 0
1
(10) (11)
(12)
written as

θ ′′ + Pr H ′θ − Hθ ′ + Q1φ = 0
1
Sc k N
N φθ ′2
(13)

φ′′ + Sc
H ′φ − Hφ′ − γφ + t φ′θ ′ + φθ ′′ − t = 0
∂u ∂w u
(1)
2
Nt θ + 1
Nt θ + 1



+ + = 0
∂x ∂z x
∂u
∂u v2
∂2u µ





ρ u ∂x + w ∂z − x = µ ∂z 2 − K u +
(2)
The boundary conditions are
H = 0,
H ′ = 0, G = 1,
θ = 1,
φ = 1 at η = 0
(14)
ρ g βt (T − T∞ )cos(α ) + ρ g βc (C − C∞ )cos(α )
H ′ = 0, G = 0,
θ = 0,
φ = 0
as η →∞
∂v
∂v uv
∂2v µ
(3)





ρ u ∂x + w ∂z + x = µ ∂z 2 − K v
Where
Da−1 = υ
is the inverse of Darcy number,
∂T
∂T
ke ∂2T
(4)
K Ω sin α

u ∂x + w ∂z = ρc
+ Q (C − C∞ )
∂z 2
β C − C
p

g βT (T − T )L3 cosα
is the Grashof number,
c ( w
∞ ) is the
∂C ∂C
∂ ∂ 2C
(5)
Gr = ω ∞
υ 2
N =
βt (Tw − T∞ )




u + w + (Cvt ) = D − kr (C − C∞ )
∂x ∂z ∂z ∂z 2

buoyancy ratio, ΩL2 cosα υ
is the local Reynolds number,
The corresponding boundary conditions are
g = Gr
is the mixed convection parameter, Pr = µC p
is the
u = 0, v = rΩ, w = 0, T = Tw ( x), C = Cw ( x)
at z = 0
(6)
s Re2 k
u = 0, v = 0, T = T∞ , C = C∞
as z →∞
Prandtl number, Sc = υ
is the Schmidt number, N = Tw − T∞ is

D T∞
where
u, v and w are tangential, circumferential and
the temperature difference parameter
Q = Q
Cw ( x ) − C∞ is

1 Ω sin α T ( x ) − T
normal velocity components along x-axis (meridional
w ∞
γ = kr
section), y-axis (circular section) and the z-axis (normal to the cone surface) directions respectively, Ω is the angular
the radiation absorption parameter and
chemical reaction parameter.
Ω sin α

is the
velocity of the rotation, ρ is the fluid density, µ is the
The physical parameters of interest local skin friction
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 200
ISSN 2229-5518
coefficients x and y-directions, local Nusselt number, local Sherwood number and wall thermophoretic deposition velocity in non-dimensional form are given by
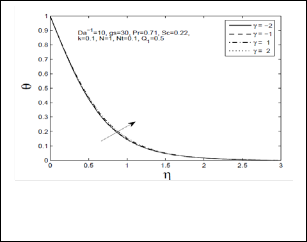
chemical reaction parameter. Fig 5 & 6 depicts temperature and concentration profiles respectively for different values of chemical reaction parameter respectively. With respect to Fig-6, it is observed that when the chemical reaction
C fx Re1/ 2 = −H ′′(0)
2−1 Re1/ 2 C fy = −G′(0) Re−1/ 2 Nux = −θ ′(0) Re−1/ 2 Shx = −φ′(0)
−k N
(15)
(16) (17) (18)
(19)
parameter increases, temperature profile increases
significantly, conversely the concentration profile decreases
as increase in the chemical reaction parameter. Therefore
we conclude that increase in chemical reaction parameter
leads to enhance thermodynamic boundary layer in y and z
direction and thermal boundary layer while it reduces
Vt =

t θ ′(0)
Nt + 1
3 NUMERICAL METHOD
velocity boundary layer in x-direction and solution
boundary layer thickness.
The non-dimensional governing equations (9) – (13) with boundary conditions (14) form highly nonlinear
Table-1: The values of
−H ′′(0), −G′ (0) and
−θ ′ (0)
for
coupled ordinary differential equations which are solved using shooting technique that uses fourth order Runge- Kutta method. In thisη = ηmax , condition at infinity, has been suitably chosen at every step such that velocity, temperature and concentration profiles approach the outer edge of the boundary layer. More calculations are performed to find the values of skin-friction coefficient, wall temperature and concentration and wall thermophoretic velocity for a wide range of parameters. The physical parameters, chemical reaction parameter, thermophoretic coefficient and thermophoretic parameters on fluid flow characteristics are studied.
In the absence of concentration equation and
inverse Darcy number the reduced eqns. of (9) – (13) similar
to Hering and Grosh [5] who investigated combined convection over a rotating cone. It is shown that numerical results of the present method are in good agreement with the results presented by Hering and Grosh [5] as shown in Table 1.
4 RESULTS AND DISCUSSION
We have presented graphical solutions for the effects of chemical reaction parameter γ on velocity,
different values of gs for Pr = 0.7, Da-1=0, and
N = 0 and in the absence of concentration equation.
gs | ʺ -H (0) | -Gʹ(0) | -θʹ(0) |
gs | Hering and Grosh [5] | Present work | Hering and Grosh [5] | Present work | Hering and Grosh [5] | Present work |
0 | 1.0205 | 1.0203 | 0.61592 | 0.61583 | 0.42852 | 0.42842 |
0.1 | 1.1369 | 1.1368 | 0.65489 | 0.65492 | 0.46156 | 0.46141 |
1.0 | 2.2078 | 2.2075 | 0.85076 | 0.85080 | 0.61202 | 0.61213 |
10 | 8.5246 | 8.5243 | 1.40370 | 1.40363 | 1.01730 | 1.01748 |
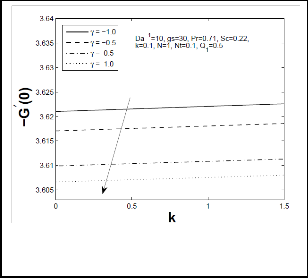
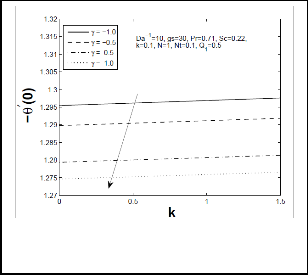
Figs 7-10 depict respectively, tangential and azimuthal skin-friction coefficient and local Nusselt number and Sherwood number for different values of chemical reaction parameter. Increasing chemical reaction
temperature and concentration profiles with distance
parameter from
γ = −1
to γ = 1 , tangential and azimuthal
normal to the cone surface. Additionally we computed the variation skin friction coefficient in x and z directions, local Nusselt number, local Sherwood number and wall thermophoretic velocity for different values of chemical reaction parameter γ , thermophoretic coefficient (k) and
temperature difference parameter (Nt ). The results of this parametric study are shown in Figs. 2-17.
Fig-2 shows the effects of chemical reaction parameter γ on tangential velocity profile (F). It is observed from this fig that increasing chemical reaction
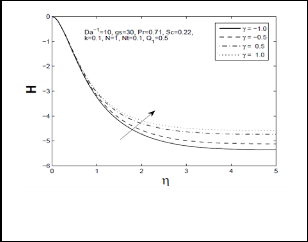
parameter retards the tangential velocity; this is due to the reduction of fluid behavior near to the cone surface when the chemical reaction parameter increases. Fig-3 & 4 show circumferential and normal velocity profiles for different values of chemical reaction parameter γ . These figures
indicate that increasing chemical reaction parameter leads to the enhancement of circumferential and normal velocity profiles for the cause of accelerating fluid motion in circumferential and normal direction by increasing
skin friction coefficients decreases. Moreover, it is observed
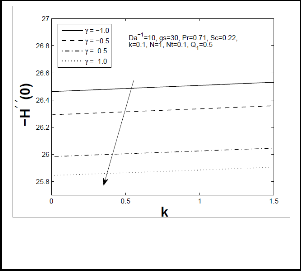
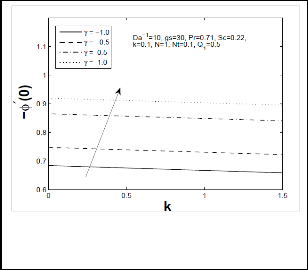
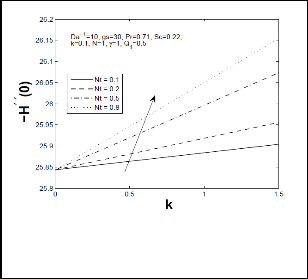
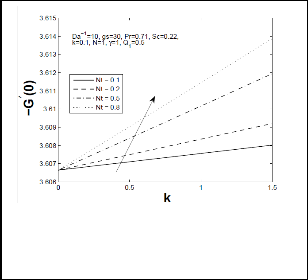
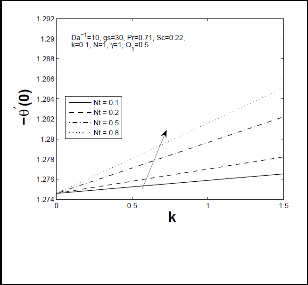
that as chemical reaction parameter increases, local Sherwood number increased enormously but the opposite results are reported for local Nusselt number. Figs 11-14 represents respectively, tangential and azimuthal skin friction coefficient, local Nusselt number and Sherwood number for different values of temperature difference parameter Nt on thermophoretic constant k. It is evident from these figures that increase in Nt increases tangential and azimuthal skin friction coefficient and local heat transfer (Nusselt number) rate but reduces mass transfer rate (local Sherwood number) significantly. Moreover, it is observed that increase in thermophoretic constant k, there is an enhancement in tangential and azimuthal skin-friction coefficient and local Nusselt number while it reduces local Sherwood number.
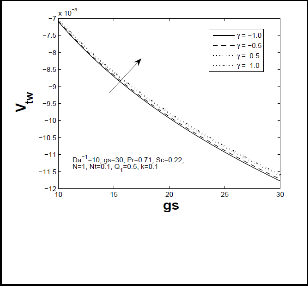
Figs 15-17 depict respectively, thermophoretic
velocity Vtw near the cone surface for different values of chemical reaction parameter γ , thermophoretic constant
and temperature difference parameter Nt. As chemical
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 201
ISSN 2229-5518
reaction parameter γ increases, wall thermophoretic
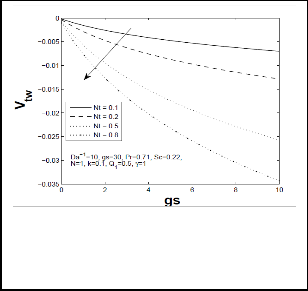
velocity increases (Fig-15). From fig-16, it is noticed that when temperature difference parameter Nt increases, there is significant depreciation in wall thermophoretic velocity. From fig-17, we perceive that increase in thermophoretic constant k decreases thermophoretic wall deposition velocity Vtw significantly. Moreover it is clearly seen that wall thermophoretic velocity decreases when increase in mixed convection parameter. These variations in thermophoretic wall deposition velocity will be significant in industrial and engineering application.
5 CONCLUSIONS
Numerical solutions are reported to analyze the chemical reaction and thermophoretic effect on rotating vertical cone in a fluid saturated Darcy porous medium. The effect of chemical reaction parameter on velocity profile in x, y and z direction and temperature and concentration profile is analyzed as well as skin friction coefficient x and z directions, local Nusselt number, local Sherwood number and wall thermophoretic deposition velocity is analyzed for different values of γ , Nt and k. It is
worth mentioning that destructive chemical reaction is more influence than generative chemical reaction parameter. As chemical reaction parameter increases, tangential velocity, concentration profiles and tangential and azimuthal skin friction coefficients and local Nusselt number decreases but circumferential and normal velocity, temperature profiles and local Sherwood number values are increased significantly. Increase in temperature difference parameter enhances tangential and circumferential skin-friction coefficients and local Nusselt number while it reduces local Sherwood number, as well as thermophoretic constant reported opposite results with those of temperature difference parameter. Wall thermophoretic deposition velocity increases when chemical reaction parameter increases but it produces opposite results for larger values of thermophoretic constant, temperature difference parameter and mixed convection parameter.
6 REFERENCES
[1] C. Tien, “Heat transfer by laminar flow from a rotating cone”,
ASME Transaction of Journal of Heat Transfer, Vol. 82, pp. 252,
1960.
[2] R. G. Hering, and R.J. Grosh, “Laminar combined convection from a rotating cone”, ASME Transaction of Journal of Heat Transfer, Vol. 85, pp. 29-34, 1983.
[3] K. Himasekhar and P.K. Sarma, “Effect of suction on heat transfer
rates from a rotating cone”, International journal of Heat and Mass
Transfer, Vol. 29, No.1, pp. 164-167, 1986.
[4] A.J. Chamkha, “Magnetohydrodynamic mixed convection from a
rotating cone embedded in a porous medium with heat generation”, Journal of Porous Media, Vol. 2, No.1, pp. 87-106,
1999.
[5] D. Anilkumar and S. Roy, “Unsteady mixed convection flow on a
rotating cone in a rotating fluid”, Applied Mathematics and
Computation, Vol. 155, 545-561, 2004.
[6] S. Roy and D. Anilkumar, “Unsteady mixed convection from a
rotating cone in a rotating fluid due to the combined effects of thermal and mass diffusion,” International Journal of Heat and
Mass Transfer, Vol. 47, pp. 1673-1684, 2004.
[7] A.J. Chamkha, S.E. Ahmed, “Unsteady MHD heat and mass
transfer by mixed convection flow in the forward stagnation region of a rotating sphere at different wall conditions,” Chemical Engineering Communications, Vol. 199, pp. 122-141, 2012.
[8] A.J. Chamkha, and A.M. Rashad, “Unsteady heat and mass
transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and soret and dufour effects,” The Canadian Journal of Chemical Engineering, Vol. 92, No.4, pp. 758-
767, 2014.
[9] A.J. Chamkha, and C. Issa, “Effects of heat generation/ absorption
and themophoresis on hydromagnetic flow with heat and mass transfer over a flat surface,” International Journal of Numerical Methods for Heat and Fluid Flow, Vol.10, No. 4, pp. 432-448, 2000.
[10] A.J. Chamkha, A.F. Al-Mudhaf, and I. Pop, “Effect of heat generation or absorption on thermophoretic free convection boundary layer from a vertical flat plate embedded in a porous medium,” International Communication in Heat and Mass Transfer, Vol. 33, pp. 1096-1102, 2006.
[11] M.K. Partha, “Thermophoresis particle deposition in a non-Darcy
porous medium under the influence of Soret, Dufour effects,”
Heat and Mass Transfer, Vol.44, pp. 969-977, 2008.
[12] M.K. Partha, “Suction/Injection effects on thermophoresis particle
deposition in a non-Darcy porous medium under the influence of Soret, Dufour effects,” International Journal of Heat and Mass Transfer, Vol. 52, pp. 1971-1979, 2009.
[13] M.M. Rahman and A. Postelnicu, “Effects of thermophoresis on
the forced convective laminar flow of a viscous incompressible
fluid over a rotating disk,” Mechanics Research Communications,
Vol. 37,pp. 598-603, 2010.
[14] A.Y. Bakier, and R.S.R. Gorla, “Effects of thermophoresis and radiation on laminar flow along a semi-infinite vertical plate,” Heat and Mass Transfer, Vol. 47, pp. 419-425, 2011.
[15] I. Muhaimin, R. Kandasamy, A.B. Khamis, and R.B. Roslan,
“Impact of thermophoresis particle deposition and chemical
reaction on unsteady non-Darcy mixed convective flow over a porous wedge in the presence of temperature-dependent viscosity,” Meccanica, Vol.48, No. 6, pp. 1415-1430, 2013.
[16] P.K. Kameswaran, P. Sibanda, M.K. Partha, and P.V.S.N. Murthy, “Thermophoretic and nonlinear convection in non-Darcy porous
medium,” ASME Journal of Heat Transfer, Vol. 136, 042601-1-9. [17] R. Bhuvanavijaya, and B. Mallikarjuna, “Effect of thermophoresis
and variable properties on free convection along a vertical wavy surface in a fluid saturated porous medium,” International Journal of Mathematical Archive,Vol. 5, No. 2, pp. 234-246, 2014.
[18] A.J. Chamkha, M. Jaradat and I. Pop, “Thermophoresis free
convection from a vertical cylinder embedded in porous
medium,” International Journal of Applied Mechanics and
Engineering, Vol. 9, No. 3, pp. 471-481, 2004.
[19] A.J. Chamkha and I. Pop, “Effect of thermophoresis particle deposition in free convection boundary layer from a vertical flat plate embedded in a porous medium,” International communications in heat and mass transfer, Vol. 31, No. 3, pp. 421-
430, 2004.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 202
ISSN 2229-5518
GRAPHS
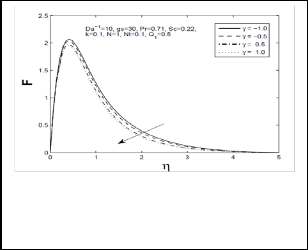
Fig.1. Physical Configuration and Coordinate system
Fig 4: Normal Velocity profile (H) for different
values of chemical reaction paramter (γ)
Fig 2: Tangential Velocity profile (F) for different
values of chemical reaction paramter (γ)
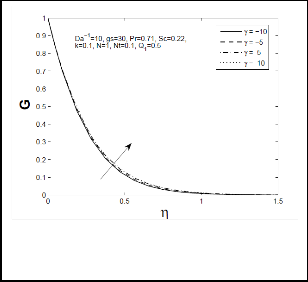
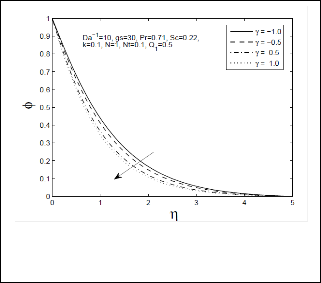
Fig 5: Temperature profile (θ) for different values of chemical reaction paramter (γ)
Fig 3: Circumferential Velocity profile (G) for
different values of chemical reaction paramter (γ)
Fig 6: Concentration profile ( ϕ) for different values of
chemical reaction parameter (γ)
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 203
ISSN 2229-5518
Fig 7: Tangential skin-friction co-efficient (Cfx) for
different values of chemical reaction paramter (γ)
Fig 10: Local Sherwood number for different values of chemical reaction parameter (γ)
Fig 8: Azimuthal skin-friction co-efficient (Cfy) for
different values of chemical reaction parameter (γ)
Fig 11: Tangentical skin-friction co-efficient (Cfx) for different values of temperature difference parameter (Nt) and thermophoretic coefficient (k).
Fig 9: Local Nusselt Number for different values of
chemical reaction paramter (γ)
Fig 12: Azimuthal skin-friction co-efficient (Cfy) for different values of temperature difference parameter (Nt) and thermophoretic coefficient (k).
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 1, January-2015 204
ISSN 2229-5518
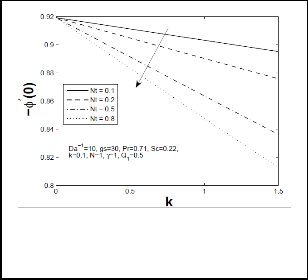
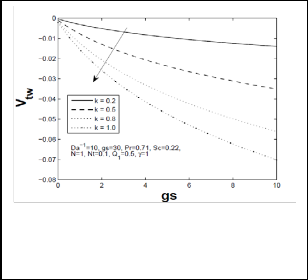
Fig 13: Local Nusselt number for different values of temperature difference parameter (Nt) and thermophoretic coefficient (k).
Fig 16: Wall thermophoretic velocity (Vtw) for different values of temperature difference parameter (Nt) and mixed convection parameter (gs)
Fig 14: Local Sherwood number for different values of temperature difference parameter (Nt) and thermophoretic coefficient (k).
Fig 17: Wall thermophoretic velocity (Vtw) for different values of thermophoretic coefficinet
(k) and mixed convection parameter (gs)
Fig 15: Wall thermophoretic velocity (Vtw) for different values of chemical reaction parameter (γ) and mixed convection parameter (gs)
IJSER © 2015 http://www.ijser.org
















