Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 1

ISS N 2229-5518

Survey of Compressive Sensing

Usham Dias, Milind Rane, S. R. Bandewar

Abs tract— In the conventional sampling process, for perf ect reconstruction of signal according to Nyquist -Shannnon sampling theorem, a band-limited analog signal has to be sampled at atleast tw ice its highest frequency. The Nyquist-Shannon sampling theorem provides a suff icient condition, but not a necessary one, f or perf ect reconstruction. The f ield of compressive sensing provides a strict er sampling condition w hen the signal is know n to be sparse or compressible. Co mpressive sensing specif ically yields a sub-Nyquist sampling criterion. Co mpressive sensing contains three main problems: sparse representation, measurement matrix and reconstruction algorithm. By now , some available measurement matrices have been discovered, such as Gaussian or Bernoulli independent and identically distributed (i.i.d) random matrices, scrambled Fourier matrix and some structurally random matrices etc. For nonlinear reconstruction, besides th e Basis Pursuit (BP) method, several f ast greedy algorithms have been proposed, such as the orthogonal matching pursuit (OMP), Regularized OMP, Co mpressive Sampling OMP. When reconstructing 2D images, besides BP, another popular method is through the minimization of total variation (min-TV) [2].

Inde x Terms— compressive sensing, sensing matrix, sparse representation, multiw avelet transf orm;

——————————  ——————————

1 INTRODUCTION

HILE the Nyquist-Shannon sampling theorem states that a certain minimum number of samples is required in order to perfectly capture an arbitrary band-limited
signal; but when the signal is sparse in a known basis we can vastly reduce the number of measurements that need to be stored. This is the fundamental idea behind CS: rather than first sampling at a high rate and then compressing the sa m- pled data, we would like to find ways to directly sense the data in a compressed form, at a lower sampling rate. CS di f- fers from classical sampling in three important respects. First, sampling theory typically considers infinite length, conti- nuous-time signals. In contrast, CS is a mathema tical theory focused on measuring finite-dimensional vectors in RN. Second, rather than sampling the signal at specific points in time, CS systems typically acquire measurements in the form of inner products between the signal and more general test functions. Thirdly, the two frameworks differ in the manner in which they deal with signal recovery. In the Nyquist-Shannon framework, signal recovery is achieved through sinc interpola- tion - a linear process that requires little computation and has a simple interpretation. In CS, however, signal recovery from the compressive measurements is typically achieved usin g highly nonlinear methods.

2 COMPRESSIVE SEN SING PAR AD IGM

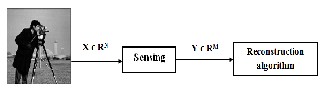
The block diagram for signal processing using compressive sensing is shown in figure 1. The scene under observation is capture using some sensing matrix, which maps the signal from N-dimensional space to M-dimensions, where M<<N. Thus it captures the signal in a compressed form, rather than sampling at Nyquist rate and then compressing. Finally the M- dimensional data needs to be reconstructed back to the N- dimensional space using efficient reconstruction algorithms.
CS theory asserts that one can recover certain signals and images from far fewer measurements M than data samples N. To achieve this CS relies on two principles:
1. Sparsity /compressibility: This reflects the fact that the in- formation contained in a signal can be much smaller that it’s effective bandwidth. CS exploits explicitly the fact that the data are economically represented in some dictionary ϕ.
2. Incoherence between the sensing modality and ϕ: This extends
the uncertainty principle between time and frequency in the sense that signals that are sparse in ϕ must be spread out in the domain in which they are acquired; that is, the sensing vectors are as different as possible from the spa rsity atoms (and vice versa), and unlike the signal, the sensing vectors must have a dense representation in ϕ.

Fig.1: Block diagram f or compressive sensing

———— ——— ——— ——— ———

 Usham Dias is currently pursuing masters degree program in signal processing in the dept. of electronics & telecomm., vishwakarma Institute of Technology, India, PH-+919823490690. E-mail:ushamdias@gmail.com

 Milind Rane is a Prof. in the dept. of electronics & telecomm., Vishwa- karma Institute of technology,India, E-mail:me_rane@yahoo.com

 S. R. Bandewar is a Prof. in the dept. of Engineering Sciences & Humani- ties, Vishwakarma Institute of Technology , India,

E-mail: srbandewar@rediffmail.com

3 SPAR SE R EPRESENTATION

In the last decade, sparsity has emerged as one of the lea d- ing concepts in a wide range of signal-processing applications (restoration, feature extraction, source separation, and com- pression, to name only a few applications). Sparsity has long been an attractive theoretical and practical signal property in many areas of applied mathema tics.
Recently, researchers spanning a wide range of viewpoints have advocated the use of overcomplete signal representa- tions. Such representations differ from the more traditional representations because they offer a wider range of generating

IJSER © 2012

http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 2

ISS N 2229-5518

elements (called atoms). Indeed, the attractiveness of redun- dant signal representations relies on their ability to economi- cally (or compactly) represent a large class of signals. Poten- tially, this wider range allows more flexibility in signal repre- sentation and adaptivity to its morphological content and en- tails more effectiveness in many signal-processing tasks (resto- ration, separation, compression, and estimation).

4 SENSING M AT RIX

The sensing mechanisms collect information about a signal x(t)
by linear functional recordings,

yk = <x, ak> k = 1, . . . , M. (1)

That is, we simply correlate the object we wish to acquire with the waveforms ak(t). This is a standard setup. If the sensing waveforms are Dirac delta functions (spikes), for example, then y is a vector of sampled values of x in the time or space domain. If the sensing waveforms are sinusoids, then y is a vector of Fourier coefficients; this is the sensing modality used in magnetic resonance imaging (MRI).
We can represent this process mathematically as

y = Ax; (2)

where A is an M x N matrix whose rows are the sensing wave- forms ak; and y ϵ RM. The matrix A represents a dimensiona l- ity reduction, i.e., it maps RN, where N is generally large, into RM, where M is typically much smaller than N. Note that in the standard CS framework we ass ume that the measurements are non-adaptive, meaning that the rows of A are fixed in a d- vance and do not depend on the previously acquired meas- urements. There are two main theoretical questions in CS. First, how should we design the sensing matrix A to ensure that it preserves the information in the signal x? Second, how can we recover the original signal x from measurements y? In the case where our data is sparse or compressible, we will see that we can design matrices A with M<< N that ensure that we will be able to recover the original signal accurately and efficiently using a variety of practical algorithms. To recover a unique k -sparse vector (a vector with atmost k < N nonzero entries) x; restrictions are imposed on A like satisfying the Null Space Property (NUS), the Restricted Isometry Property (RIP) and or some desired Coherence.

5 RECENT AD VANC ES

Currently, researchers always use orthogonal wavelet to represent the images. But the wavelet only has single scaling function and cannot simultaneously sa tisfy the orthogonality, high vanishing moments, compact support, symmetry chara c- teristic and regularity. Developed from the theory of wavelet, multiwavelet transform, can simultaneously satisfy the five characteristics, and provides a great potential to obtain high performance coding. Paper [7], proposes a compressive sens-
ing image reconstruction based on sparse representation of the image in multi-wavelet transform domain while using Or- thogonal Matching Pursuit iterative as the reconstruction algo- rithm. To evaluate CS reconstruction, they deploy both the OMP and DMWT (discrete multi-wavelet transform) using random Gaussian and Bernoulli measurement and compare the results using 256 x 256 standard gray-scale image. Image reconstruction in compressive sensin g using multiwavelet transform and wavelet transform are much better than using discrete cosine transform. Furthermore using multiwavelet domain is better than using wavelet domain. The result of CS reconstruction using Gaussian measurement from M=150, 170 ,
190 are shown in Table I. According to the comparison in Ta- ble I, it is confirmed that image reconstruction for compressive sensing using multi-wavelet and orthogonal matching pursuit is better.

TABLE I: RESULTS USING GAUSSIAN MAT RIX

Comparing PSNR for the image of reconstruction at several measurements M x N (N=256), it was noted that, the more measurements M are taken, the better the quality of image reconstruction it is. The result of CS reconstruction using Ber- noulli measurement from M=150, 170, 190 are shown as fol- lows:

TABLE II: RESULT S USING BERNOULLI MAT RIX

Most of existing methods for CS image reconstruction are suitable for piecewise smooth image, but do not behave well on texture-rich natural image. In paper [2], a new optimization problem for CS image reconstruction is proposed, in which different regularization terms are introduced for different morphological components of image. Experimental results show that the proposed method can be applied to reconstruct texture-rich images besides piecewise smooth ones, and ou t- performs the existing methods on preserving detail features. For nonlinear reconstruction methods, besides the BP method

IJSER © 2012

http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 3

ISS N 2229-5518

several fast greedy algorithms have been proposed, such as the orthogonal matching pursuit (OMP), the tree-based OMP and the stage-wise orthogonal matching pursuit (StOMP). Other algorithms include iterative soft-thresholding and pro- jection onto convex sets, etc. When reconstructing 2D images, besides BP, another popular method is through the minimiza- tion of total variation (min-TV). The min-TV method assumes that the image is gradient sparse and usually offers recon- structed images with better visual quality. Unfortunately, these two methods and other relevant techniques are not ap- propriate to reconstruct texture-rich natural images. The tex- ture feature is often smoothed during the reconstruction process. Paper [2], proposes a new optimization problem for image reconstruction by taking advantages of morphological component analysis (MCA), which can preserve texture fea- ture while not degrading the visual quality of whole image as shown in table III.
In paper [8], CS reconstruction problem of images are dis- cussed from a multivariate point of view. Most conventional wavelet-based CS reconstruction methods assume that the wavelet coefficients are mutually independent. However, si g- nificant statistical dependency exists among the wavelet coef- ficients of images. The statistical structures of the wavelet c o- efficients are considered for CS reconstruction of images that are sparse or compressive in wavelet domain. A multivariate pursuit algorithm (MPA) based on the multivariate models is developed. Several multivariate scale mixture models are used as the prior distributions of MPA. Their method reconstructs the images by means of modelling the statistical dependencies of the wavelet coefficients in a neighbourhood. Multivariate algorithms proposed here present superior performance com- pared with some state-of-the-art CS algorithms.
In CS applications, the acquisition of the linear projections Ax requires a physical implementation. In most cases, the use of an i.i.d. Gaussian random matrix A is either impossible or overly expensive. This motivates the study of easily impl e- mentable CS matrices. Two such matrices are the Toeplitz and circulant matrices [9], which have been shown to be almost as effective as the Gaussian random matrix for CS encod- ing/decoding. In toeplitz matrix, every left-to-right descend- ing diagonal is constant, i.e., T i,j = Ti+1,j+1. If T satisfies the addi- tional property that ti = tn+i; for all i where n is the number of
columns, it is also a circulant matrix C. An m x n general ma- trix has mn degrees of freedom, but a partial circulant matrix of the same size has at most n degrees of freedom. Hence, a random circulant matrix is generated from much fewer inde- pendent random numbers or is much less random than an i.i.d. random matrix of the same size. This fact seemingly su g- gests that a random circulant matrix would yield less incoher- ent projections, and consequently worse CS recovery. How- ever, numerical results in [9] show that circulant matrices can be equally effective as i.i.d. random matrices.
In paper [10], they investigate signal recovery procedure for the case where A is binary and very sparse. They show that, both in theory and in practice, sparse matrices are essentially as ―good‖ as the dense ones. At the same time, sparse binary matrices provide additional benefits, such as reduced encod- ing and decoding time. They als o report experimental results which indicate that, in practice, binary sparse matrices are as
―good‖ as random Gaussian or Fourier matrices when used in
Linear programming(LP) decoding (both in terms of the nu m- ber of necessary measurements, and in terms of the recovery error). At the same time, the LP decoding is noticeably faster for sparse matrices.

6 CONCLUSION

Compressive sensing has changed the way the intellectual community deals with signals especially its acquisition and compression. It provides a necessary condition for sampling and faithful reconstruction of signal, whose bounds are much lower than the conventional Nyquist sampling theorem. The main challenges in compressive sensing are to select the best sparse representation for the signal, measurement matrix for acquisition and algorithm for reconstruction. Research is mov- ing from the conventional DFT, DCT and wavelet sparse d o- mains to multi-wavelet, contourlet, curvelet, ridgelets and bandlets. Gaussian and Bernoulli matrices were the first few sensing matrices discovered. But they are inefficient for hard- ware implementation. Therefore the intellectual community is looking for sparse matrices as potential candidates to replace the dense random matrices. Toeplitz and circulant matrices are also being used as measurement matrix. Basis pursuit and orthogonal matching pursuit (OMP) has proved efficient for reconstruction of sparse signals. Other algorithms which can

TABLE III: COMPARISON OF T HREE RECONST RUCT ION MET HODS (PSNR IN DB)

IJSER © 2012

http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 4

ISS N 2229-5518

be considered are the Tree-Based OMP, stage-wise OMP and compressive sampling matching pursuit (CoSAMP).

ACKNOWLEDGM ENT

We would like to extend our sincere thanks to Prof. Milind Kamble, Dept. Of Electronics & Telecommunication, Vishwa- karma Institute of Technology, for his help in the field of op- timization.

REFERENCES

[1] Donoho D L., “Compressed sensing”, IEEE Transactions on Information The- ory, 2006, 52(4): 1289-1306.

[2] Xingxiu Li, Zhihui Wei, Liang Xiao, Yubao Sun, Jian Yang, “Com-

pressed sensing image reconstruction based on morphological component

analysis”, IEEE 2009

[3] E. Candes and T. Tao, ―Decoding by linear programming‖, IEEE Trans. Inform.

Theory, 51(12):4203-4215, 2005

[4] First-Year Report, “Restricted Isometry Property (RIP)”, Graduate School of

Mathematics University of EdinburghSeptember, 2009

[5] Ming-Jun Lai, “On Sparse Solutions of Underdetermined Linear Systems”, Depart-

ment of Mathematics, the University of Georgia, Athens, GA 30602, January 17,

2009.

[6] Jean-Luc Starck, Fionn Murtagh, Jalal M. Fadili, “Sparse image and signal proc-

essing: Wavelets, Curvelets, Morphological Diversity”, 2010.

[7] Fan Yang; Shengqian Wang; Chengzhi Deng; “Compressive Sensing of Image

Reconstruction Using Multi-wavelet Transforms‖, IEEE International Conference

on Intelligent Computing and Intelligent Systems (ICIS), 2010, vol. 1, Page(s):

702 – 705

[8] Wu, J.; Liu, F.; Jiao, L. C.; Wang, X.; Hou, B.; “Multivariate Compressive Sensing for

Image Reconstruction in the Wavelet Domain: Using Scale Mixture Models”, IEEE

Transactions onImage Processing, Vol.20, Issue:12 , 2011 , Page(s): 3483 - 3494 [9] Wotao Yina, Simon Morganb, Junfeng Yangc, Yin Zhanga; “Practical Compressive

Sensing with Toeplitz and Circulant Matrices”

[10] Radu Berinde, Piotr Indyk; “Sparse recovery using sparse random matrices”, April

26, 2008

[11] Deanna Needell, “Topics in Compressed Sensing”, Dissertation for Doctor of

philosophy inMathematics, University of California, Davis, 2009.

[12] Philip Breen, ―Algorithms for Sparse Approximation‖, Year 4 Project, School of

Mathematics, University of Edinburgh, 2009

IJSER © 2012

http :// www.ijser.org