International Journal of Scientific & Engineering Research, Volume 3, Issue 4, April-2012

ISSN 2229-5518

Speed of convergence. CEE and Western

Balkans countries

Enton Duro

Abstract — The implications of neoclassical model in growth theory are still dominant. One of the implications is convergence hypot hesis which means that in the long run income per capita will converge in the steady state level. W ith regards it is suggesting a nat ural methodology for finding support of convergence hypothesis. Different researches found the speed of convergence for different “convergence club” countries and regions around the world. Regarded to this it is suggested” convergence club” countries for Albania which is composed by Central, Eastern Europe (CEE) and Western Balkans countries because of same similar characteristics. The observed period for this study is 2000-2010 and the explanatory variable is GNI per capita. In this study, after testing the convergence hypothesis in cross-sectional data set through regression analyses, it is estimated the speed of convergence around

2% per year between this “convergence club” country.

Index Terms— “Convergence club” for Albania, Convergence of income per capita, GNI, Mathematical neoclassical model of growth, Speed of convergence.

1. INTRODUCTION

——————————  ——————————
lbania and other similar countries are in the process of European integration, process of which determines an achievement of certain requirement. There are different countries with similar historical facts, countries. Countries like Estonia, Latvia, Lithuania, Poland, Czech Republic, Slovakia, Hungary and Slovenia in May 2004, and in January 2007 Ro- mania and Bulgaria, are now part of EU. Other countries like Albania, Macedonia, Serbia, etc are trying to make possible this participation. Being part of the EU required obligation of achieving determinant objectives in different spheres of life and one of them are economic criteria. Candidate and poten- tial candidate countries need to converge in common objec- tives. For this reason it is looking for convergence of income
per capita between these countries.
First part of this study illustrated the concept of conver-
gence which will be tested. Literature review about pro and
cons convergence hypothesis is suggested in the second part.
Then, in the third part, mathematical model of convergence
explain how to pose the convergence problem and how to
quantify the response of them. The fourth part of the study
trying to constructs ―convergence club‖ countries for Albania
according similarities between them. The last part represents an empirical finding by cross-sectional regression analyses in SPSS 17.

2. THE CONCEPT OF CONVERGENCE

Beyond the history neoclassical model was mostly consi- dered by the researchers to predict convergence in term of income per capita. The pioneers of neoclassical model are So- low [16], [17] and Swan [20]. Considering diminishing return of physical capital in production, which is the crucial assump- tion in contest of convergence, they conclude that a closed economy will converge in its steady state in term of income per capita, or more detailed, in the presence of exogenous

————————————————

Enton DURO is currently pursuing PhD program in Economics in Uni- versity of Tirana. He is assistant of professor in macroeconomics in depart- ment of Economics in Faculty of Economy UT. E-mail: du- ro7enton@gmail.com
technological progress income per capita will grow only by the rate of technological progress. In the neoclassical model steady state level depends on the depreciation rate of physical capital, the growth rate of population and the rate of saving. Differences in these country indicators, which are considered constant in time, saving rate, population growth and deprecia- tion, make the differences in steady state level. On the basis of the neoclassical assumptions endogenous saving rate taking in consideration optimal consumption choice by individual in time and the result is the same, in the long run an economy will converge in steady state level of income per capita [3], [7], [19]. This means that each country, in the long run, will con- verge at its steady state level. So, lower the level of income per capita, compared to steady state level, higher should be rate of growth for achieving long run equilibrium.
Researches considering these theoretically frameworks have constructed a convergence terminology. Absolute conver- gence refers to the process by which relatively poor countries grow faster that rich ones. The notion of absolute convergence maybe implies that county indicators are the same for all, or more exactly, these indicators are dynamically related to the economic growth and evolve together. Countries may have a common steady state and, in the long run, they can grow at the same rate, rate of exogenous technological change. Rea- sons for absolute convergence should be: (i) lower level of cap- ital means higher marginal returns which push increasing in- vestments and, in the same time, income to steady state level, (ii) the contagion of poor economies from successful economic model of richer can push them towards steady state level. Conditional convergence implies that a given country con- verges to its steady state and this level depends on the indi- vidual county indicators. By this definition it is not necessary to argue that poor counties grow faster than rich ones. How largest is the rate of growth of a given country depends by the distance of its own steady state. This mean that poor countries can have a lower growth rate even that they level of income per capita is lower than rich counties. Reasons for conditional convergence should be: (i) Even though a higher return of cap- ital in poor countries, they cannot increase investment because of higher necessity to consume and, in the open economy, be-

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, April-2012

ISSN 2229-5518

cause of higher risk and uncertainty that characterize these countries which is called ―poverty trap‖ in literature, (ii) even though successful model are available poor countries do not have ―the capacities‖ to adopt them. However, conditional convergence permits to analyze, after controlling for steady state differences, a negative relation between growth and ini- tial level of income per capita in the same way of absolute convergence.

3. LITERATURE REVIEW OF CONVERGENCE

The most important assumption that makes possible a presence of convergence in theory is diminishing return of capital. If this condition is not held than income per capita for a given economy do not converge and consequently even the world. In fact, for better explanation of growth emerged new theory of endogenous growth. Romer [11], [12] and Lucas [15] use an excellent theoretical framework to explain that dimi- nishing return of capital is not held in general. Based in AK model, through external effect of knowledge, R&D and inno- vation, Romer explains that a given country will not converge in term of GDP per capita. Lucas, considering human capital performance and learning by doing in the production process which leads in increasing returns to scale, interprets the same
growth rate from 1960 to 2000 is not related with the Log of GDP per capita in 1960 using cross-country data for 112 coun- tries; even more they found a positive relation intending a presence of divergence [14].
This literature review suggests that, with more probability, the hypothesis of conditional convergence is more present in the world. Conditional convergence into the world or absolute
convergence between ―convergence club‖ and regions make reasonable the agreement of similarities of them. The diffusion of technology, the influence of social mentality and their be- havior, the political condition and decision, the representation of democracy by institutions, openness of economy, and all of that unexplored in growth theories, tend to be more similar in these kind of ―convergence club‖ or regions.

4. MATHEMATICAL NEOCLASSICAL MODEL OF GROWTH WITH CONSTANT SAVING RATE

Assuming Cobb Douglas production function with labor augmenting technological progress [2]. Technological progress transforms the labor input in effective labor input Y= F(K;AL). In the Cobb Douglas function production by labor and capital inputs is given
conclusion of non convergence.
The sustention of convergence comes at firs by Abramovitz
[10] who explains the negative relation between initial level of
Y
(1)



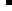
K (AL)1
productivity and growth rate of productivity in the long run.
Where technology and labor input are supposed to be
He defines ―catch up‖ the process which make possible that poor can catch rich in term of productivity. Baumol [21] using Maddison data [1], introduced the term of ―convergence
A(t) L(t)

e gt
L 0 e nt


AL e gt
L 0 e nt

L 0 e

( n g)t

clubs‖. The idea of clubs is that if a homogenous sample of
countries can be founded, than according to neoclassical mod-
This means that this factor grows constantly in time by n+g. In

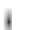
terms of capital per effective worker we have
el absolute convergence should be observed. He found a nega-



k K(t) L 0 e( n g)t
K(t)


~ ( n g)t
kL 0 e
tive relation between average rate of growth and initial level
GDP per work hour during the period 1870-1979 by the equa-
tion g= 5.25- 0.75ln(Y1870) R2=0.88 for 16 countries called
Where the first derivate per time (t) should be equal to saving in a closed economy
them clubs. Making attention of the ratio of standard devia- tion from the mean of GDP per work-hour, Baumol concluded
~

K k L0 e

(n g)t

~
k(n

g)L0 e

(n g)t

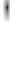
sF K; L0 e

(n g)t

(2)
that it is fallen quite steadily. Mankiw, Romer and Veil using augmented Solow model by human capital, founded a signifi-
Divided per effective worker we have ~
~
k(n


g) sf( ~) . If we
cant tendency toward convergence for OECD sample [8]. After
take in consideration depreciation rate by (σ) than we take
controlling for rate of saving, population growth and human capital they explained that convergence hypothesis is relevant.




~ sf(~) (n g ~
(3)
One of the regression results offered by them is the speed of
In the Cobb Douglas case we have

convergence around 2% per year. The contribute in conver- ~ ~
gence hypothesis is offered by Barro and Sala-I-Martin where k k



(n g ~
(4)
they have investigated the US data set for 48 states and have suggested a 2% annum as a speed of convergence between them [13]. The same rate of convergence was suggested by

At steady state capital per effective worker will not change, so

k 0 . If we consider output per effective worker equal to

~

Sala-I-Martin from Japanese prefectures [23]. However, abso-

y~ k

in the steady state physical capital per effective worker
lute convergence it is not present in the world. Mankiw, Ro-

will be taken by sk (n

g)k . By transformations we
mer and Veil conclude that unconditional convergence is not
present in their data. Sala-I-Martin did not find absolute con-
get steady state level of capital per effective worker which is

1

vergence between 110 countries for the period 1960-1990 [23]. ~ s 1
The set of countries in the world did not converge in the sense k*
of beta convergence1. Barro and Sala-I-Martin suggested that n g
(5)
And output per effective worker converges in

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, April-2012

ISSN 2229-5518

1

y~ * s 1

n g

(6)
This term is called beta convergence. The negative sing is jus- tified by the fact that does not make sense negative speed of convergence if the capital per effective worker does not achieve steady state. The rapport of the formula is negative
The right side of the expression is composed by constants.
We have assumed population, technology and depreciation are changed constantly in time. This formulation explains why steady state level should be different for different countries. Output per capita (effective worker) in steady state depends
because of the opposite movement of the components multip- lied per minus makes β positive. We can obtain them by con- sidering absolute value of the first derivate of the right side of
1.10 by ln ~



~
on saving rate, population growth, technological change and
(1 )sk (1 )
(12)

depreciation. To consider growth rate of output we can write
Speed of convergence is negatively related to the level of cap-

y~*

1

Y(t s 1

A(t)L(t) n

Y(t)

1

s 1 A(t)L(t)

n

ital per effective worker. This means that, when we are at low- er level of steady state, speed declines as we approach to the steady state, so β is not constant. In the equation (12) we can
If we like to have growth rate of per capita output we can fol-

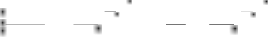
low
substitute the value of capital per effective worker in steady
state given by equation (5) and then, after simple transforma-

Y (t

1

s 1 y

Y (t)

1

s 1 A(t)

tions, we have

A(t)L(t) n

L(t) n

* (1

)(n g)

(13)

For facilities we consider

1

This is the steady state for β. Speed of convergence, in this
equation, represents how rapidly capital per effective worker

s 1 approaches to the neighborhood of steady state level. So, we

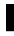
n g can write

Growth rate of output will be equal to

'

~ ~ ~ ~
k k k k *
(14)

Y A(t )L(t) t

A L(t )

L A(t ) A

L g n

A(t )L(t)

A(t )L(t )

A(t )

L(t )

(7)
Consider Cobb Douglas of (1) we can be written







~ ~ ~ ~

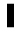
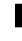
And growth rate of per capita output will be
'
y~ y~
k k or
ln y~ y~ ln k k
y φA(t) t g
φA(t)
(8)
Using (11) and (14) it can be written
This formulation demonstrates what we have mentioned be- fore. For a given country growth rate in steady state converges

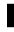
y~ y~

* ln

y~ y~ *

(15)
in population growth plus technological change or, growth rate of output per capita converges in technological change. These are the conclusions of neoclassical model.

4.1. SPEED OF CONVERGENCE

Consider equation (4) we can find rate of change of capital per effective worker in any time by
Equation (15) says that growth rate of output per effective worker to the neighborhood of steady state, is equal to the speed of convergence multiplied by the gap between steady state and actual level. Again, if countries have the same steady state level poor country will grow faster than rich by the catch up process. The solution of this differential equation can give the equation of testing convergence hypothesis. Equation (15) can be written


~ ~ ~ ~

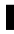
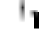
(ln y~)'

[ln y~

ln y~ ]

(16)
k k s k


k (n g)

(9) t

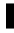
This may be written as

~

Substituting lny~ = z we have z
(z(t)

z ) . Here z0=z(0)

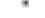
~ ~ ~ (1 )

(1 ) ln k

and z* is steady state. For more we have

k k sk

(n g) se

(n g)

(10)
So, the rate of change of capital per effective worker declines as its value converges to steady state. Here we can introduce the concept of speed of convergence. It measure how much the rate of change decreases as its level increases in proportional

z z(t) z *
Considering integrating factor lying both sides

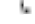
tdt

(t) e
(17)

e t and multip-
sense (i.e. by 1%). By formulas it can be written

e t z
e t z(t)

e t z *
(18)

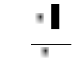
~ ~ Integration of (18) gives
k k
ln ~
(11)
z(t) z


Ce t
(19)

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, April-2012

ISSN 2229-5518

Initial condition of starting point will have that z0=z(0) and
(PPP).

z(0) z

C where C


z(0) z
Differential solution will be
Kornai [9] suggested different characteristics that make simi-
z(t)


z * [z(0)


z*]e t
(20)
lar CEE countries during 1990-2004 in the convergence
Substitution of Ln(y)=z(t) give

TABLE 1

ln y~

[1 e

t ]ln y~ * e

t ln y~ 0

(21)

NOMINAL CONVERGENCE CRITERIA FOR EU MEMBER STATES

Here
ln y~ 0
is the natural logarithm of initial level of output
per effective worker. Subtract in both parts of (21) by ln y~ 0 we


have

ln y~

y~ 0

[1 e

t ]ln y~ 0

[1 e

t ]ln y~ *

(22)
In this equation we can see that growth rate is explained by initial level of income per capita and by steady state level of income per capita, all in term of effective worker. If we assume that technology is exogenous and growth by constant rate g, the equation (22) can be formulated in the same way in term of
income per capita adding the constant g. Also [1 e

t ]ln y~ *

is no longer an explanatory variable if we consider the abso- lute convergence. Passing from the deterministic definition of hypothesis to the stochastic process we have to consider a normal distribution of the random disturbance in the process by the term ui. For the given interval of time [0;T] we can write

1 ln y

T i;T

yi;0

a [1

e T ] T

ln yi;0

ui;o,T

(23)
process. He called ―great transformation‖ the process of tran- sition of these countries because of: direction of market econ-
Here a


g [1 e

*T ]ln y~ *

is supposed to be the same for all
omy and democracy: parallel complete transformation in all
the economies and
ui;o,T
is the random disturbance of the
spheres, the transformation was not violent and peaceful in
data. Now we have a regression form of absolute convergence hypothesis.

5. CONVERGENCE CLUB COUNTRIES FOR ALBANIA

It is not a simple way to define a ―convergence club‖ because of the heterogeneity of social aspect of Europe countries. Countries with millennium history and culture are significant- ly non similar between them. Even thought, there are same characteristics which can make possible candidate countries for building ―convergence club‖ for Albania. CEE and West- ern Balkans countries can construct a given ―convergence club‖ for Albania. During 1989-1990 all these countries passed from a planned to a free market economy. After that, all of these countries have been evolved in the integration process in EU. Some of them are now part of EU realizing at least nomin- al convergence stipulated in the Treaty of Maastricht called nominal convergence. The fulfillment of these criteria‘s is as- sessing the possibilities of sustainable economic growth under the conditions of promoting the public policies of achieving the convergence process in real term. Real convergence is de- fined as incomes convergence, prices convergence, productivi- ty convergence, educational standards convergence, infra- structure development, economic and social cohesion, struc- tural convergence with EU economies, etc. One of most impor- tant indicator of real convergence remains income per capita
sense of no use of military intervention, the incredible speed of
transformation. Marelli and Signorelli [5] believe that the core
of ―great transformation‖ was the institutional change, which interacts with additional spheres: economic growth and de- velopment, structural change and economic performance, in- equality and labor market, relations and shocks in global
shocks in the global economy. These countries can be defined as a vanguard of ―convergence club‖.
One of the most structural factors, which make possible the convergence, is the adoption acquis communautaire. Contin- ued work in structural convergence along the lines of the ac- quis communautaire is crucial also in candidates like Macedo- nia, Montenegro and Croatia, and potential candidate coun- tries like Albania, Bosnia Herzegovina, Serbia and Kosovo.
For Balkan countries the characteristics of convergence club are stronger. Central European Free Trade Agreement (CEF- TA) have positive impacts in the regional integration process expanding trades and eliminating barriers between countries, providing protection of intellectual property rights, harmoniz- ing policy and competition strategies facilitating sustainable growth and development in Balkan. This second group of countries completes the ―convergence club‖ for Albania,
which is evidently the last position in terms of Income per capita (PPP).

6. DATA ANALYSES OF ABSOLUTE CONVERGENCE

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, April-2012

ISSN 2229-5518

We are going to test for absolute beta convergence hypothe-

ln y~

[1 e

t ]ln y~ * e

t ln y~ 0

satisfies the condition e-βt=1/2.
sis using data for CEE and Western Balkans countries because
of the ―convergence club‖ characteristics. Log linear Regres-
sion between average of per capita income growth and log of
initial income per capita is to be tested for absolute conver-
gence hypothesis. The period observed in the cross-sectional
data, due to particular conditions, is 2000-2010. The crisis of
‗97 in Albania and the war of Ex-Yugoslavian countries in 1999
may cause problems in the normal trend of data. By this facts,
initial level of income per capita starts from 2000. In the data
analyses is considered GNI per capita. In fact migration factor
is present in different countries in the sample. Romania, Bul- garia, Estonia, Albania, Montenegro, Bosnia Herzegovina and others, showed a migratory movement towards western coun- tries after 1990. GNI maybe reflect better the technological level, human and social capital and preferences embodied in national population. All this factors are considered significant in growth literature. Turning to the data analyses SPSS pro- gram is used to test the convergence hypothesis by OLS me- thod and the regression is given by the equation

11

The halfway in time is therefore [Ln(2)/β]=0.69/0.02. If we consid- er the result for β=0.02 we can establish the time t=34.4 years. This means that starting from the initial condition of income per capita only after 34 years will be in halfway of achieving the steady state level.

7. CONCLUSION

Absolute convergence hypothesis, implied by neoclassical model, consists in the process by which poor countries can thatch up rich ones. This hypothesis is not supported by em- pirical studies for the world. It is more acceptable conditional convergence hypothesis which means that counties with simi- lar characteristics can converge in the term of income per capi- ta creating ―convergence club‖. For Albania ―convergence club‖ can be represented by CEE and Western Balkans coun- tries because of, the similar characteristics in changing from commanded to free market economic system, facing to the European integration process in achieving nominal conver-
gence postulated by Treaty of Maastricht and the adoption of

g t T

t 0

b0 b1 ln y i;0

u i;o ,T

(24)
acquis communautaire, the common economic agreement like
CEFTA, etc. Considering cross-sectional data set for the period
200-2010 and using OLS method is estimated that speed of absolute convergence (β convergence) toward steady state level is around 2% per wear. Anyway, the model can explain
30 % of the variation in average of income per capita growth
rate.

REFERENCES

Fig. 1. Average growth rate for the 2000-2010 and Ln of GNI per capita 2000. It is easy to understand the trend of data given in this graph. Anyway, we can see that the dispersion is considera- ble regarding to the trend. Source W B 2012 and own calculation.

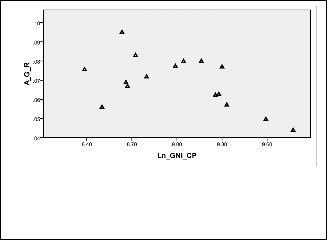
Regression results are in support of the theoretically frame- work. It is found negative coefficient of Ln y0 (b1=-0.018) and it is statistically significant at 5%. The model can explain 30.2% of the variation in average of income per capita growth rate (R square =0.302) and residuals seems to have normal distribu- tion. By calculation of the speed of convergence, the rate of which Gross national income per capita tends to steady state level, is around 2% per year by this calculation

[1] A. Maddison,‖Phases of Capitalist Development” Oxford, Oxford

University Press, 1982.

[2] D. Acemoglu, ―Labor- and Capital-Augmenting Technical Change‖

http://web.mit.edu/daron/www/lab-cap5.pdf , Jan. 2000.

[3] D. Cass, ―Optimum growth in an aggregative model of capital accu-

mulation,‖ Review of Economic Studies, pp.32, 233–240, 1965.

[4] D. Raluca and C. Mirela, ―Romania between real and nominal con- vergence,‖ University of Craiova, Faculty of Economy and Business Ad- ministration, 2007 http://steconomice.uoradea.ro/anale/volume/2007/v2-finances- accounting-and-banks/62.pdf.

[5] E. Marelli and M. Signorelli, ―Economic Growth and structural fea-

tures of transition‖ pp. 11-56. PALGRAVE MACMILLAN Ba- singstoke, Hampshire RG21 6XS, 2010.

[6] European Commission http://www.cefta2006.com/

[7] F. P. Ramsey, ―A Mathematical Theory of Saving‖, the Economic Jour-

- 0.018 = - (1 - e -

*11 ) 11. Barro and Sala-I-Martin suggested

nal, Vol. 38, No. 152. (Dec), pp. 543-559, Dec. 1928.

that the time for which Ln(y(t)) is in the halfway between Ln(y0) and Ln(y*) is given by Lucas rule 70/β. Lucas explain that considering y as a income per capita at time t and let y0 be some initial value of per capita income. Then y=y0egt.The time it takes per capita income to double is given by the time t* at which y=2y.Therefore, 2y0=y0egt implies t*=Ln2/g. Re- garding to Barro and Sala-I-Martin (2004) is suggested that halfway convergence is the time for which equation

[8] G. Mankiw, D. Romer, D. Weil , ‖A Contribution to the Empirics of Economic Growth,‖ The Quarterly Journal of Economics, Volume 107, issue 2, pp. 407 – 437, May 1992.

[9] J. Kornai, ―The great transformation of Central Eastern Europe: Suc- cess and Disappointment, “Economics of Transition, pp. 2, 14, 207-244, Apr. 2006.

[10] M. Abramovitz, ―Catching Up, Forging Ahead and Falling Behind.‖

Journal of Economic History: 385-406. Jun. 1986.

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, April-2012

ISSN 2229-5518

[11] P. Romer, ―Endogenous Technological Change,‖ The Journal of Politi- cal Economy, Vol. 98, No. 5, Part 2, pp. S71-S102, Oct.1990.

[12] P. Romer, ―Increasing Return and Long-Run Growth,‖ The Journal of

Political Economy, Vol. 94, Issue 5, pp. 1002 – 1037, Oct. 1986.

[13] R. Barro and X. Sala-I-Martin, ―Convergence‖, journal of Political

Economy, 100 (May): 223-252, May 1992.

[14] R. Barro X. and Sala-I-Martin, ―Economic Growth‖, 2nd edition, pp.

23-71, 462-496. The MIT Press Cambridge, Massachusetts, 2004.

[15] R. E. Lucas, ―On the mechanics of Economic Development,‖ Journal of

Monetary Economics 22, pp. 3-42, Feb. 1988.

[16] R. M. Solow, ―A Contribution to the Theory of Economic Growth,‖

the Quarterly Journal of Economics, Vol. 70, No. 1, pp. 65-94, Feb. 1956. [17] R. M. Solow, ―Technical Change and the Aggregate Production Func-

tion,‖ the Review of Economics and Statistics, Vol. 39, No. 3, pp. 312-320,

Aug. 1957.

[18] R. Martin and A. Winkler, ―Real Convergence in Central, Eastern and South-Eastern Europe‖ pp. 68-88, 124-152. PALGRAVE MACMIL- LAN Basingstoke, Hampshire RG21 6XS, 2009.

[19] T. Koopmans, ―On the concept of optimal economic growth,” Eco- nometric Approach to Development Planning, chap. 4, pp. 225–87, 1965.

[20] T. Swan, ―Economic Growth and Capital Accumulation,” Economic

Record 32.63, pp. 334-361, 1965.

[21] W. J. Baumol, ―Productivity Growth, Convergence, and Welfare: What the Long Run Data Show,” IU American Economic Review 75,

1072-85, Aug. 1985.

[22] World Bank http://data.worldbank.org/topic/economic-policy-and- external-debt

[23] X. Sala-I-Martin, ―The classical approach to convergence analysis” Economics working paper 117, Yale University and Universitat Pompeu Fabra, Jun. 1995.

ANNEX TABLE 2

REGRESSION INPUT DATA

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, April-2012

ISSN 2229-5518

Bulgaria 0.082936 6150

TABLE. 3

REGRESSION OUTPUTS

a. Dependent Variable: A_G_R

TABLE. 4

MODEL SUMMARY

a. Predictors: (Constant), Ln_GNI_PC
b. Dependent Variable: Av_G_R

IJSER © 2012

http://www.ijser.org