International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 2005

ISSN 2229-5518

Soliton Solution to the (3+1)-dimensional Kadomtsev-Petviashvili Equation by the Tanh-Coth Method

Anwar Ja'afar Mohamad Jawad, Ali A. J. Adham

Abstract Exact travelling wave solutions are obtained to the (3+1)-dimensional Kadomtsev-Petviashvili equation and (2+1)- dimensional equation by means of the tanh-coth method. New solitary wave solutions are got. The method is applicable to a large variety of nonlinear partial differential equations. The outcome of this method will be powerful to solve (3+1)-dimensional, it was difficult to obtain the solution in this case.

Index Terms: Exact solution, Kadomtsev-Petviashvili equation, tanh-coth method, nonlinear partial differential equations.

——————————  ——————————

1. INTRODUCTION

oliton can be defined as a solution of a nonlinear partial differential equation. Solitons are found in many physical phenomena. Solitons arise as the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems. Solitons are solitary waves with elastic scattering property. Due to dynamical balance between the nonlinear and dispersive effects these waves retain their shapes and speed to a stable waveform after colliding with each other. One basic expression of a solitary wave solution is of

the form [1]:
These types of waves will not change their shapes during propagation and are thus easy to detect. Of particular interest are three types of travelling waves: the solitary waves, which are localized travelling waves, asymptotically zero at large distances, the periodic waves, which rise or descend from one asymptotic state to another. Recently, algebraic method, called the mapping method [2-3], is proposed to obtain exact travelling wave solutions for a large variety of nonlinear partial differential equations (PDEs). This method includes several direct methods as special cases, such as tanh-function method[4], sech-function method, and tanh-coth method[5].

u( x, t ) =

f ( x − λt )

(1)

1.1. The Kadomtsev-Petviashvili (KP) Equation

where λ is the speed of wave propagation. For λ > 0 , the wave moves in the positive x direction, whereas the wave moves in the negative
The nonlinear dispersive equation formulated
by Korteweg and de Vries (KdV) in its simplest
form is (1+1) dimensional equation and is given by [6]:
x direction for λ < 0 .
Travelling waves, whether their solution

ut − 6uux

+ uxxx = 0

(2)
expressions are in explicit or implicit forms are

with u = u( x, t )

is a differentiable function.
very interesting from the point of view of applications.

Corresponding Author:

Anwar Ja'afar Mohamad Jawad

Al-Rafidain University College , Baghdad, Iraq

anwar_jawad2001@yahoo.com

Co-Author

Ali A. J. Adham

Faculty of Technology University Malaysia

Pahang,

aliadham@ump.edu.my

We shall assume that the solution u( x, t ) , along with its derivatives, tends to zero as | x |→

∞.
In 1970, Kadomtsev and Petviashvili
generalized the KdV (1+1) dimensional equation to two space variables (2+1) dimensional equation and formulated the well-known Kadomtsev- Petviashvili equation to provide an explanation of the general weakly dispersive waves [7]. They developed this equation when they relaxed the restriction that the waves be strictly one- dimensional of the KdV equation.

1.2. The (2+1)-dimensional Kadomtsev-

Petviashvili equation

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 2006

ISSN 2229-5518

The (2+1)-dimensional Kadomtsev-Petviashvili equation is given by:
This paper aims to implement tanh-coth method to determine solitary solution for the
(3+1)-dimensional KP equation.

(ut − 6uux + uxxx ) x + α .u yy = 0

(3)

where u = u( x, y, t )

is a real-valued function

2. OUTLINE OF TANH-COTH METHOD

of two spatial variables x and y, and one time variable t, and α is a constant scalar. When
For a given nonlinear evolution equation, say, in four variables

α = 0 , Eq. (3 ) reduces to the KdV equation

Eq.(2). When

α < 0 , the equation is known as

P(u, ut , u x , u y , u z , u xx ..........) = 0

the KP-I equation which is a good model when surface tension is strong and dominates in very
(7)
We seek a travelling wave solution of the form:
shallow water. However, for

α > 0 , the

u(ξ , y , z, t ) = U(ξ )

equation is called the KP-II equation which is a good model when surface tension is weak or
, and

ξ = kξ + αy + βz + ωt + θ0

absent. In other words, the coefficients

α > 0

(8)
and

α < 0

are used for weak surface tension
Where

k ,α , β , ω,θ0

are constants. The
and strong surface tension respectively. This
means that the two KP equations have different
physical structures and different properties. The
following chain rule

∂U = ω dU ,

∂U = k dU ,

KP equation is used to model shallow-water
waves with weakly non-linear restoring forces. It
is also used to model waves in ferromagnetic media. Several analytical and numerical

∂t

∂U = α

∂y

dξ

dU ,

dξ

∂x dξ

∂U = β dU ,

∂z dξ

approaches were employed to solve the KP equations. The KP solutions have been studied extensively to derive periodic and soliton

∂ 2U

∂x 2

= k 2

d 2U

dξ 2

solutions.[1]

1.3. The (3+1)-dimensional modified Korteweg-

converted the PDE Eq.(3), to an ordinary
differential equation ODE

de Vries (kdV) equation

Q(U ,U / ,U // ,U /// ,..........) = 0

(9)
The (3+1)-dimensional modified Korteweg-de
Vries (kdV) equation is given by [8]:
with Q being another polynomial form of there argument, which will be called the reduced

u + 6u 2u

+ uxyz = 0

(4)
ordinary differential equations of Eq.(9).
and the Solitary wave solution is given by
Integrating Eq.(9) as long as all terms contain
derivatives, the integration constants are

u( x, y, z, t ) = ±

c2 c3 sec h

(5)
considered to be zeros in view of the localized solutions. However, the nonzero constants can be

[c1 x + c2 y + c3 z − c1c2 c3t + δ ]

1.4. The (3+1)-dimensional KP equation

The (3+1)-dimensional KP equation given by
[9,10].
used and handled as well. Now finding the traveling wave solutions to Eq.(9) is equivalent to obtaining the solution to the reduced ordinary differential equation Eq.(9).
The key step is to introduce the ansatz, the
new independent variable

(ut + 6uux + uxxx ) x + α (u yy + uzz ) = 0

(6)

Y = tanh(ξ )

(10)
Mohammed [11] constructed new exact
traveling wave solutions of the (3+1) dimensional
that leads to the change of variables:
Kadomtsev-Petviashvili (KP) equation, in which the homogeneous balance method is applied to solve the Riccati equation and the reduced

dξ

d 2U

= (1 − Y 2 ) dU

2 dU 2 2

nonlinear ordinary differential equation,
respectively.

dξ 2

= −2Y (1 − Y

) + (1 − Y )

dY 2

Peng et al [12] obtained exact travelling wave

d U =

− Y 2

Y 2 − dU

solutions in terms of the Jacobi elliptic functions to the (3+1)-dimensional Kadomtsev-Petviashvili
equation by means of the extended mapping

dξ 3

2(1

)(3

d 2U

d 3U

method.

− 6Y (1 − Y 2 ) 2 + (1 − Y 2 )3

dY 2

dY 3

(11)

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 2007

ISSN 2229-5518

The next step is that the solution is expressed in the form [12]

k 4 [−2Y (1 − Y

2 ) dU

+ (1 − Y

2 ) 2

d 2U

]

dY 2

U (ξ )

= ∑ aiY

i + ∑

i =

biY

(12)

+ AU + 3 k 2U 2 = 0

i 1

where the parameter m can be found by balancing the highest-order linear term with the nonlinear terms in Eq.(9), and
where:

A = [kω − 3(α 2

+ β 2 )]

(15)
(16)

k ,α , β , ω, a0 , a1 ,...., am , b1 ,...., bm

are to be determined. Substituting Eq.(12) into
Eq.(9) will yield a set of algebraic equations for
Now, to determine the parameter m, we balance the linear term of highest-order with the highest order nonlinear terms. So, in Eq.(15) we balance

k ,α , β , ω, a0 , a1 ,...., am , b1 ,...., bm

U 2 with

U // , to obtain:

because all coefficients of Y have to vanish.
m+2 = 2m , then m = 2. The tanh-coth method admits the use of the finite expansion for :
Having determined these parameters, knowing

U = a

+ a Y + a Y 2 + b Y −1 + b Y −2

that m is positive integer in most cases, and using

0 1 2 1 2

Eq.(12) we obtain analytic solutions u( x, t )

closed form.
,in a
and

U / = a

+ 2 a Y − b Y −2 − 2b Y −3

The hyperbolic functions can be extended to trigonometric functions by using the complex

1 2 1 2

and

// −3 −4

form. So that a tan-function expansion solution generates from a tanh function expansion solution

U = 2 a2 + 2b1Y

+ 6b2Y

(17)
for

Y = tanh(iξ ) = i tan(ξ )

, and a cot-
Substituting

U / ,U //

from Eq.(17) in Eq.(15),
function expansion solution generates from a coth function expansion solution for

Y −1 = coth(iξ ) = −i cot(ξ )

. The tanh-coth
then equating the coefficient of Y i , i= 0, 1, 2, 3,
4, -1, -2, -3, -4 leads to the following nonlinear system of algebraic equations:

method seems to be powerful tool in dealing with
nonlinear physical models [13].

Y : −4k 4 [a

+ 4b2

] + Aa0 +

3. APPLICATIONS

3 k 2

[a 2

+ 2(a1b1 + a2b2 ) = 0

3.1. Exact solutions to the (3+1)-dimensional

KP equation

Y : −2 k

[ a1 + 3b1 ] + Aa1 + 3k

a0 a1 = 0

The (3 + 1)-dimensional KP-I equation is given by [9,10]:

Y : 4k 4 a

+ Aa2

+ 3k 2 ( a a

+ a 2 ) = 0

(ut + 6uux + uxxx ) x − 3(u yy + uzz ) = 0

Y : 2 k

a1 + +3k

a1 a2 = 0

(13) This explains wave propagation in the field of plasma physics, fluid dynamics, etc. Soliton simulation studies for Eq.(13) have been done by

4 3 k 2 a2 = 0

−1

4 + + 2 + =

Senatorski et al. [14].

Y : 10k b1

Ab1

3k (a0b1

a1b2 ) 0

To study the travelling wave solutions to Eq.(13), substitute u( x, y, z, t ) = U (ξ ) , and

−2

Y : 28k b2 +

Ab2

+ 3 k

(2a0b2

+ b2 ) = 0

ξ = kx + αy + βz + ωt + θ 0

into Eq.(13)

−3

: −4 4

+ 3 2 = 0

and integrating twice, we have:

Y k b1

−4

k b1b2

k 4U // + [kω − 3(α 2 + β 2 )]U

(14)

Y : −8k 4 b

+ k 2 b 2 = 0

+ 3 k 2U 2 = 0

Solving the nonlinear systems of equations (18)
we postulate tanh series , and the transformation given in Eq.(10), so that Eq.(14) reduces to:
we can get

a1 = 0 ,

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 2008

ISSN 2229-5518

A + 3(α 2 + β 2 )

ω = , and

b1 = 0 with

a = 4 +

14 k 2 a

− k 2

the following cases:
Case 1

0 3

− k 2

, 2 3 ,

a = −4 k 2

b2 = ,

2 2

A = −2

14 k 3

0 3

A = 16 k 3

, a2 = −2 k ,

b2 = −2 k ,

u = k 2 [ 4 +

14 − 1 tanh 2 ( ζ ) − 1 coth 2 (ζ )]

u = −2k 2 [ 2 + tanh 2 (ζ ) + coth 2 (ζ )] (19)

1 3

7 3 3 3

(25) Case 8
Case 2

2 2

2 a0

= 4 −

14 k 2

a = − k

a0 = 4k ,

a2 = −2 k ,

b2 = −2 k ,

3 , 3

A = −16 k 3

− k 2

u = 2k 2[2 − tan h2 (ζ ) − coth 2 (ζ )]

(20)
, b2

= , A = 2

14k 3

Case 3

u = k 2 [ 4 −

14 − 1 tanh 2 (ζ ) − 1 coth 2 (ζ )]

a = 4 +

14 k 2 2

8 3 3 3

0 3

− k 2

, a2

= −2k

,
(26) Results of solving (3+1) dimensional KP in this

b2 =

A = −2

14 k 3

paper are compatible with that results obtained by
Wazwaz [15] for the (2+1) dimensional KP

u = k 2 [ 4 +

14 − 2 tanh 2 (ζ ) − 1 coth 2 (ζ )]

(21)
equation.

For k = α = β

= 1, θ0

= 0 , the solitary

Case 4
solution in Eq.(19) becomes:

a = 4 −

14 k 2 2

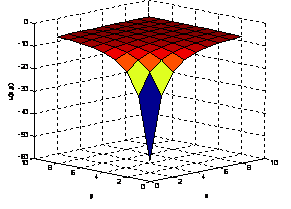
u ( x, y, z, t ) = −2[ 2 + tanh 2 ( x+y + z + 22t )

0 a = −2 k 1 3

, ,

b2 =

− k 2

, A = 2

14 k 3

+ coth 2 ( x+y + z + 22t )]
and is shown in figure (1) for given
(27)

t, x, y, z

u = k 2 [ 4 −

14 − 2tanh 2 (ζ ) − 1 coth 2 ( ζ )]

.
(22)
Case 5

− k 2

a = 4 −

14 k 2

a2 =

0 3 , 3 ,

b2 = −2 k

, A = 2

14 k 3

u = k 2 [ 4 −

3

14 − 1 tanh 2 (ζ ) − 2 coth 2 (ζ )]
3
(23)
Case 6

a = 4 +

0 3

14 k 2

a = − k

2 3 ,

Figure (1) Solitary solution for

0.1 ≤ x ≤ 1 , t = 0, z = 0

0.1 ≤ y ≤ 1 ,

b2 = −2k ,

A = −2

14 k 3

3.2. Exact solution to the (2+1)-dimensional

u = k 2 [ 4 +
3

14 − 1 tanh 2 ( ζ ) − 2coth 2 ( ζ )]

3
(24)

equation

The (2 + 1)-dimensional equation
Case 7

uxt − 4uxuxy − 2u y uxx + uxxxy = 0

(28)

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 2009

ISSN 2229-5518

Substituting

u( x, y, t ) = U (ξ ) ,and

For

a0 = 1, k = α

= 0.5,θ0

= 0 the

ξ = kx + αy + ωt + θ0

into Eq. (28) and
solitary solution in Eq.(33) is
integrating once with zero constant, we have:

u( x, y, t ) = 1 − 2 coth[ x + y − 4t ]

k 2αu /// + ωu / − 3kαu / 2 = 0

(29)
and is shown in figure (2).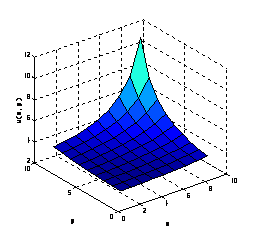

we postulate the following tanh series , and the transformation given in Eq.(4), then Eq.(29) reduces to:

k 2α[2(1 − Y 2 )(3Y 2 − 1) dU − 6Y (1 − Y 2 ) 2 d U

dY dY 2

+ (1 − Y 2 )3 d U ] + ω[(1 − Y 2 ) dU ] − 3kα[(1 − Y 2 ) dU ]2 = 0

dY 3 dY

(30)
Now, to determine the parameter m, we balance the linear term of highest-order with the highest order nonlinear terms. So, in Eq. (30) we balance

U / 2 with

U ///

, to obtain m+3 = 2m+2 , then
m=1. The tanh-coth method admits the use of the finite expansion for :

U = a

+ a Y + b Y −1

Figure (2) solitary solution u(x,y) for

t = 0.5 ,

0 1 1

and

U / = a − b Y −2

, = 2b1Y ,

0.1 ≤ x ≤ 1 , 0.1 ≤ y ≤ 1 .

and U

///

= −6b1Y

(31)

4. CONCLUSION

Substituting U / ,U // ,U /// from Eq.(31) in Eq.

Y i

The exact travelling wave solutions to (3+1)- dimensional KP and (2+1)- dimensional equations
(30), then equating the coefficient of
, i= 0, 2,
have been studied by means of tanh-coth method.
4, -2,-4 leads to the following nonlinear system of algebraic equations:

It can be easily seen that the implemented methods used in this paper are powerful and applicable to a large variety of nonlinear partial

Y : −2k

α (a1 + b1 ) + ω (a1 + b1 )

differential equations.

− 3kα (a1 + b1 )

− 6kαa1b1 = 0

REFERENCES

Y : 8k αa1 − a1ω + 6kα (a1 + b1 )a1 = 0

(32)

[1] Wazwaz A. M. , Partial Differential Equations and

Solitary Waves Theory, Higher Education Press, Beijing and Springer-Verlag Berlin Heidelberg , 2009.

Y : −6k 2αa

−2

− 3kαa 2 = 0

[2] Peng Y.-Z. Acta Phys. Pol. A 103, 417 , 2003.

[3] E. Yomba, Chaos, Solitons and Fractals 21, 209 , 2004.

[4] Jawad A. J. M , Petkovi'c M. D. , Biswas A. , Soliton

Y : 8k

−4

αb1 + ωb1 + 6kα (a1 + b1 )b1 = 0

solutions of a few nonlinear wave equations, Applied

Mathematics and Computation journal, Vol. 216 , pp.

Y : −6k 2αb

− 3kαb2 = 0

2649–2658 , 2010.

[5] Parkes E. J. , Observations on the tanh-coth expansion

Solving the nonlinear systems of equations (32)
we can get:

a1 = −2 k , ω = −16k 2α , b1 = −2 k

method for finding solutions to nonlinear evolution

equations, Appl. Math. Comput. Vol. 217 , pp. 1749–

1754, 2010.

[6] Drazin P, G., and Johnson R.S., Solitons: an

Introduction, Cambridge University Press, Cambridge,

u = a0 − 2k

[tanh(kx + αy −16k αt + θ 0 )

(33)

(1996).

[7] Kadomtsev B. B. and Petviashvili V. I., On the stability

+ coth(kx + αy −16k αt + θ 0 )]

u = a0 − 4k coth[2(kξ + αy − 16k 2αt + θ 0 )]

(34) Remark: the solitary solution (34) is verifying the problem equation in (28).

[11] Mohammed K., New Exact traveling wave solutions of the (3+1) dimensional Kadomtsev-Petviashvili (KP)

of solitary waves in weakly dispersive media, Sov. Phys. Dokl., 15, 539–541, 1970.

[8] Willy Hereman, Exact Solutions of Nonlinear Partial

Differential Equations The Tanh/Sech Method, Wolfram Research Inc., Champaign, Illinois October

25– November 11, 2000.

[9] Ablowitz M., Segur H., J. Fluid Mech. 92, 69, 1979.

[10] Kuznietsov E.A. , Musher C.L., Exp J.. Theor. Phys. 63,

947 , 1986.

equation, International Journal of Applied

Mathematics, vol. 37 : 1 ,2007.

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 2010

ISSN 2229-5518

[12] PengamY. Z., and Krishnanb E. V., Exact Travelling Wave Solutions to the (3+1)-Dimensional Kadomtsev- Petviashvili Equation, Acta physica Polonica A, Vol.

108 ,2005.

[13] Abdou M. A. , The extended tanh method and its

applications for solving nonlinear physical models, Applied Mathematics and Computation journal, Vol.

190 , 988–996,2007.

[14] Senatorski A., Infed E., Phys. Rev. Lett. 77, 2855 (1986). [15] A. M.Wazwaz, Multiple-soliton solutions for the KP

equation by Hirota’s bilinear method and by the tanh–

coth method, Applied Mathematics and Computation

190 , 633–640, 2007.

The Author: Dr. Anwar Ja'afar Mohamed Jawad was born in Baghdad, Iraq (1961). He is one of the academic staff in Al-Rafidain University College, Baghdad-Iraq. He is an Assistant professor in Applied Mathematics. The academic Qualifications are PhD. in Applied Mathematics from University of Technology, Baghdad, (2000), M.Sc. in Operation Research from University of Technology,

Baghdad, (1989), and B.Sc. in Mechanical Engineering from Baghdad University, (1983). He is interested in Differential equations, and Numerical analysis. He published in international journals more than 40 manuscripts in solving nonlinear partial differential equations. He was teaching Mathematics, numerical analysis for graduate and postgraduate students in Iraqi and Syrian universities. He was a supervised for many MSc. and PhD. thesis.

Co-Author: Dr. Ali A. J Adham : In 1995, was obtained his B.SC from Mosul University/Iraq, Faculty of Computer Science and Mathematics. In 2005, he obtained the M.SC degree from University of Technology/Iraq, Faculty of Applied Science. The PhD degree obtained from University Malaysia Pahang/ Malaysia in 2012. His interest is in Applied Science and Operation Research. He has teaching experience more than 16 years in several universities and Colleges in teaching many subjects under computer science, operation research, and Mathematic.