with
Converges to at most one point at X.
In this context Kasahara S. proved a
Lemma.
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 956
ISSN 2229-5518
ANJALI SANT
Head of the department of Basic Science Bhopal Institute of Technology and Science, Bhopal (M.P.) India.
Abstract: In this paper the concept of L- SPACE is introduced and common fixed point theorems proved for commuting mappings in L-space.
L-Space was introduced in fixed point theory by S. Kasahara in 1976.It is observed that in many fixed point theorems the metric properties ,in particular the axioms of triangle property ,are not essential in their proofs.
Let N denote the set of all non- negative integer. A pair (x →) of a set X and a subset → of the set XN XX is called an L-space if the following two conditions are satisfied:
1. If xn=x ԐX for all nԐ N, then
({xn }n ԐN, x) Ԑ→ 2. If ({xn }n ԐN, x) Ԑ→,then ({xni } iԐ N, x) Ԑ→For every subsequence {x ni } I Ԑ N →of {xn} n ԐN We shall write {x n} n ԐN→ or {xn} →x, instead of {x n} n ԐN, X Ԑ→, and read {xn } n ԐN converges to x.We require some definitions:
space (X’, →) is said to be continuous if x n→x
implies f (xni )→’f(x) for some subsequence
{xni } i ԐN of {xn } n ԐN.
≤∞ for all x, y in X.The L-space(X, →) is said
to be complete if each sequence {x n } n ԐN in X
with
Converges to at most one point at X.
In this context Kasahara S. proved a
Lemma.
RELATED WORK
d(x ,y) = d(y ,x)=0, implies x=y for every x ,y in X.During the past few years many great mathematicians worked on L-space, respectively their names are Kasahara S.(1,2),Iseki(3),Singh(4).More recently, Pachpatte,B.G.(5,6) and Pathak H.K. and Dubey R.P.(7,8) gave very interesting results in L-space.In 1988, Pathak and Dubey proved theorem. THEOREM: (P.D)- Let (X, →) be a separated L-space which is d-complete for a non-negative real valued function d on X xX with d(x, x)=0 for each x in X. Let E, F and T be three continuous self mappings of X satisfying the conditions.
1. ET=TE, FT=TF , F(X)Ϲ T(X) and
E(X) Ϲ T(X) and
2 .d (Ex, Fy) ≤α 
For all x, y in X where α,β≥0 and α+β
˂1 with T x ≠ Ty.
Then E, F and T have a common fixed point. Further, if α, β ≥0 and α+β ˂1 then E, F and T have a unique common fixed point. Further, Sharma and
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 957
ISSN 2229-5518
Agrawal proved the following theorem in their paper (9).
1. ET=TE, FT=TF,E(X)ϹT(X) and F(X) Ϲ T(X)
2.d(Ex,Fy)≤α. 
+
For all x, y in X where α,β≥0 and α+β ˂1 with
T x ≠ Ty.
Then E, F and T have a common fixed point. Further, if α, β ≥0 and α+β ˂1 then E, F and T have a unique common fixed point. Our object in this paper is to extend and generalize the results of Jungck (9), Pathak and Dubey (6), Sharma and Agrawal (8) in fact we prove- MAIN RESULT
1.1. ET=TE,FT=TF,E(X)ϹT(X) and
F(X) Ϲ T(X)
1.2.d(Ex,Fy) ≤ α
+
Tx2n+2 =Fx2n+1 ………… (b)
Now we consider,d(Tx2n+1, Tx2n+2 ) =d(Ex2n,
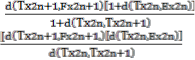
Fx2n+1 )
≤α
+β
+
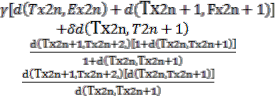
= α
+β
+
=
(α+β+γ)d(
Therefore, we haved(Tx2n+1, Tx2n+2 )≤ (α+β+γ)d(
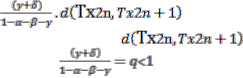
Hence,d(Tx2n+1,Tx2n+2 )≤
= q. Where Sinceα+β+2γ+δ˂1.Forn=1,2,3..whetherd(Tx
2n+1, Tx2n+2 )=0 or not similarly we have, d
(Tx2n+1, Tx2n+2 ) ≤ qn .d(Tx0, Tx1 )for every positive integer n this means that
For all x, y in X where α, β,
≥0 and α+β+2
+
˂1 with Tx ≠ Ty. Then E, F and T have a common fixed point.
Let x0 Ԑ X. Since E(X)ϹT(X).We can choose a point x, in X such that Tx1=Ex0 also F(X) Ϲ T(X).we can choose a point x2 in X such that Tx2=Fx1. In general we can choose the points.
Tx2n+1 =Ex2n …………… (a)
…. (b) Thus the d-completeness of the space implies that the sequence {Tnx0 } n ԐN converges to some u in X. So by (a) and (b).{Enx0 } n ԐN and
{Fnx 0 } converges to same point u respectively.
Since E, F and T are continuous, there is a subsequence t of {Tnx 0 } n ԐN such that E(T(t))→E u ,T(E(t))→T u ,F(T(t))→Fu and T(F(t))→T u Hence by (1.1), we have Eu=Fu=Tu……………………..(c)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 958
ISSN 2229-5518
Thus, T(Tu)=T(Eu)=E(Tu)=E(Eu)=E(Fu)=T(Fu)=F(Tu
)=F(Eu)=F(Fu)………………………..(d) Therefore by (1.2), (c) and (d) we have,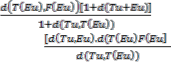
If Eu ≠F(Eu)
d(Eu, F(Eu)≤α
+β.
+γ[d(Tu,Eu)+d(T(Eu),F(Eu))]
+δ.d (Tu, T(Eu))
≤δ. d( Tu, T(Eu)) Thus we get a contradiction,
Hence E u=F (E u)……………………. (e)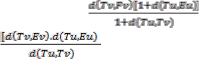
From (d) and (e) we have, E u=F (E u)= T(E u)=E(E u). Hence E u is a common fixed point of E, F, and T. F or uniqueness, Let u, v (u≠ v) is two common fixed points of E, F and T. Then by (1.2) we have d (u, v)=d(E u, F v)
≤ α
+β. +γ[d(Tv,Fv)+d(Tu,E u)]
+δ. d(T u, T v)
Therefore, d (u,v) ≤ δ. d (u,v). Again a contradiction. Therefore u=v Thus T, E, and F
have a unique fixed point.
1. If we put α=γ=0 then we get the result of Pathak and Dubey (6)
2. If we put β=γ=0 then we get the generalized form of the result of Sharma and Agrawal (8).
3. If we put α= β=γ=0 then we get the
result of Jungck in L-space.
4. If we put α=γ=0 then we get the generalized form of the result of Jaggi, D.S. in L-space.
Self- mappings of X satisfying (1.1)
and (1.3)
d(Epx,Fqy) ≤
+β 
+γ [d (T x, Ep x)+Ty, Fq y]
+δ. d (Tx, Ty) for all x, y, in X. Tx ≠Ty α, β,
≥0 and α+β+2
+
˂1
If some positive integer p, q exist such
that EP , Fq and T are continuous. Then
E, F,T have a unique common fixed point in X.
PROOF: It follows from (1.1) Ep T=TEP, Fq T=T Fq, Eq(X)Ϲ T(X) and Fq(X)Ϲ T(X) by theorem 1,there is a unique fixed point u in X such that, u=Tu=Epu=Equ……………………..(f) That means u is the unique fixed point of T, Ep, Fq .Now T (E u)=E(T u)=E(u)=E(Epu)=Ep(Eu)…………….(g). And T (Fu)=F(T u)=F(u)= F(Fq u)=Fq (Fu)………………………
………...(h)
Hence in follows that E u is a common fixed point of T, Ep and Fu is a common fixed point of T and Fq. The uniqueness of u from (f), (g), and (h) implies, u=E u=Fu=T u
This completes the proof.
2.1. EFT=TEF, FET=TEF, EF(X) ϹT(X) and
FF(X) Ϲ T(X)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 959
ISSN 2229-5518
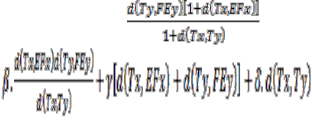
2.2.d(EFx,FEy)≤α +
For all x, y in X where α, β,
≥0 and α+β+2
+
˂1 with T x ≠ Ty. Further if T, E F and FE are continuous, Then E, F and T have a common fixed point.
PROOF: Let EF=S1 and FE=S2 , then by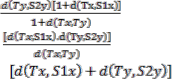
(2.2),we have d(S 1x,S2 y)≤α
+β
+γ
+δ.d (T x, T y)
Holds for all x, y in X with T x ≠Ty and α,β, 
≥0 and α+β+2 
+ 
1 and the conditions S2T=TS2,S1T=TS1,S1(X)Ϲ T(X) and S2(X)Ϲ T(X) are satisfied. Further by theorem 1 there exists a unique point u such that, u=S1u=S2 u=T u Also E u=E (S2u) =EF (E u) = S1 (E u) and F (S1u)=FE(Fu)=S2(Fu) This means that E u is a fixed point of S1 and Fu is a fixed point of S2 .The uniqueness of u Implies u=E u=Fu=T u. This completes the proof. REMARKS: If we put F=1, we get the result of theorem 1.
(5)Pachpatte B.G. Common fixed point theorems for certain mappings in L-space
(6)Pathak H.K. and Dubey: Some common fixed point in L-space MACT Vol.13 (1980)
(7)Pathak H.K. and Dubey: common fixed point of three commuting mappings in L-space MACT Vol.13 (1980)
(8)SHARMA AND AGRAWAL: Common fixed points in L-Space Actacienia India Vol.XVIII on 4,681(1991)
(9)JUNGEK: Commuting mapping and fixed point AMER.MATH.MONTHLY,83 (1976),261-263
REFERENCES
(2) Kasahara. S. Common fixed point theorem for mappings in L-spaces Math. Semi. Notes Volume (1975)
(3) ISEKI. On common fixed point theorem of mapping. Math. Semi. Notes Kobe Uni. Japan,
10 (1982), 96-98
(4)Singh. Some common fixed point in L-space
Vol.7 (1979) Math. Semi. Notes.
IJSER © 2014 http://www.ijser.org