International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 40

ISSN 2229-5518

SER analysis for the best relay selection with interferences for DF

Edriss Eisa Babikir Adam1,2, Li Yu1 and Rabiu HARUNA1

1 Huazhong University of Science &Technology, Wuhan National Laboratory for Optoelectronics, Division of Communication & Intelligent Networks, Wuhan 430074, Peoples R China

2 Department of Electrical Engineering, Faculty of Engineering, University of Blue Nile, Roseires, Sudan

e-mail: bonzoga20@yahoo.com, hustlyu@hust.edu.cn and maizare@gmail.com

Abstract— In this paper, we analyze the performance of a new cooperative diversity scheme based on best relay selection with interferences at relay nodes, only relay node can be affected by interference. For the selection scenario, only a best relay that maximizes the end-to- end received signal-to-interference and noise ratio (SINR) at the destination is selected to forward the information. Through statistical analyses, we establish a closed-form expression for the symbol error rate (SER), by deriving the analytical expressions for the probability density function ( PDF ), the cumulative density function ( CDF ), and the moment generating function (MGF) of the instantaneous received signal to interference and noise ratio (SINR) from relay selection. At relay nodes we use selection combiner (SC), which only process one of the diversity branches that has the highest SINR, alternatively, at the destination we used maximum ratio combiner (MRC) to combine the transmitted signals from the source and that one from the best selected relay. we show that our new scheme optimizes well the available resources (two channel links: the direct and the best relay links). Simulations are given to validate the analytical results with different number of relays and different interference power.

Index Terms— Wireless network, Best relay selection, Decode-and-Forward, symbol error rate, Multiple interferences.

——————————  ——————————

1 INTRODUCTION

ooperative diversity obtained without implementing multiple antennas on small communication terminals. By using virtual antennas (relays) between
source and destination the full diversity will occur.
Cooperative diversity is a cooperative with virtual antennas for improving, network channel capacities. In cooperation communication, the surrounding users act as relays to help in forwarding information to the destination to achieve full diversity[1].Cooperative diversity can be implemented by helping of the Intermediate nodes called relays. So, relaying strategy concept has become an interesting field of research and has been widely investigated [2]. Therefore, one of the most advantages of using it in wireless networks is that the event of having all relay nodes goes down is very low. So the destination can receive multiple copies of the initial information sent from the source by applying some relaying protocols such as the amplify-and-forward (AF), decode- and-forward (DF)[3]. In amplify-and-forward protocol, the relay station amplifies the received signal from the source and forwards to the destination, whereas in Decode-and- Forward (DF) protocol, the relay forwards the information to the destination after decoding it. At the destination, the receiver detects the total information from the combination of transmitted signals from the source and that one from the relay nodes, using one of the combination methods[4]. Nevertheless, relay selection is employed to work in cooperative systems to make improvements to the multi- relay networks in which n+1 signals are required for a
number of relays n [5]. And as a consequence in a multi- relay nodes technique, a bandwidth penalty might be observed caused by the presence of n+1 time slots. Therefore, relay selection goes obviously to be a highly interesting field which requires to be taken into account with an aim to fill the gap of investigation in wireless cooperative communication systems by efficiently using the channel resources. Within this paper, only two time slots are required to help the transmission scheme: one for the direct link and one for the best selected relay link.
Multiple Relay based communication is very susceptible to interference due to the fact the interference influences equally the received signal at the relay, as well as the received signal at the destination. Interference is a major infection in wireless cooperative communication systems. Multiple relay networks exploit a number of intermediate nodes known as relays to allow connection between source and destination; hence, the probability of interference affect the system is very high. On the other hand, the performance gains of cooperative systems are affected by multiuser interference, because the incoming signals can interfere with adjacent cells, especially in urban scenarios with many users and cells close to each other. That is why many researchers consider the effect of interference in cooperative network using relay selection, [6-9]. Minghua Xia and Sonia Aïssa[10] investigated the performance of cooperative with AF protocol, With the effect of interference powers at primary

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 41

ISSN 2229-5518

users and the Nakagami-m fading parameter of the interference channels. The authors in [11-13] found that the relays can decode and forward or amplify and forward the information if channel’s coefficient is above or below certain threshold. The authors in [11] proposed a decode-and- forward (DF) relay selection scheme using max-min criterion for an interference-limited multiple relay network, they derived bit error rate (BER) and outage probability under the effect of interference. J. B. Si et al. [12], proposed a threshold-based relay selection protocol for wireless relay networks with interference to choose one best relay to forward the information, in which the interference associated with the chosen relay is below. Amplify-and- forward strategy for interference limited networks in [13], is considered, in [14] the authors investigated the interference aware relay assignment using a heuristic algorithm (IRA). Work in [15] proposed three cooperative algorithms to obtain suboptimal solutions for end-to-end sum-rate maximization challenge in a multiple-antenna amplify-and- forward (AF) relay interference channel.
In this paper, we consider a multiple relays network in which, only the best relay that can be used to maximize the end-to-end received SINR in term of (SER) furthermore we assumed that the relay can decode the transmitted information perfectly which mean that the source relay link couldn’t be affected by noise or interferences. The perfect channel side information (CSI) available at the receiver
is considered. Assuming also that main channel gains are

channel (any two nodes in the network is subject to Rayleigh fading) and additive white Gaussian noise (AWGN) N0

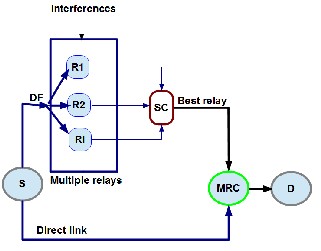
Fig.1. System model

The transmission scheme can be divided into two phases. In phase 1, the source broadcasts the information to the N relay nodes and the destination simultaneously. So the received signals at the ith relay (considering the effect of interferences), and the destination (D) are respectively given by:
known to the transmitter, the signals can be transmitted

Ysd 

PS hsd x  nsd

(1)

through orthogonal channels by using some common access

Ysr 

PS hsr x 

PS hsr x  nsr

(2)

techniques such as TDMA, FDMA or CDMA. For a simple

i i i i

analysis, we use the TDMA system.
The rest of this paper is organized as follows: Section 2 a
Where:

Desired

Int erferences

system model of best relay using DF protocol is presented.

Ysd

and Ysr
represent the received signal at the destination
Section 3 discusses SINR analysis and show how we can select the best relay after making some derivation of PDF, and CDF. Asymptotic symbol error rate (SER) and MGF are analyzed in Section 4. Simulation results and Conclusion are provided in Section 5 and 6 respectively.
and ith relay respectively and hsd , hsr are the fading channel coefficient between source S to destination D and between source and ith relay, nsd and nsr denote the additive white
Gaussian noise (AWGN) with variance N0 , x and PS are transmitted information symbol and transmitted source

2 SYSTEM MODEL

power ( PS
normalized to unity), on the other hand x
As in fig. 1, our cooperative relay network system consisting of one source node S and N cooperative relays Ri;(i
=1,2….,N) with L interferences at relay nodes and one
destination D. The channels from S to Ri and from Ri to D are
modeled for interfered cluster as transmitted information
symbol with fading channel coefficient hsr .
And in part 2, the selected best relay ri forwards the signal received from Source to Destination as follows:
statistically mutually independent, and identically

 P h 

P h x  n

(3)

distributed (i.i.d.). The system works under Rayleigh fading

Yr d r

ri d x

ri

rid

ri d

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 42

ISSN 2229-5518

Where, x and x are the decoded information at the relay ri
for both desired and interfered signals respectively.

γS  Ps

hsd

N0  and SINR for relay link, they follows

exponential distribution with parameters λS  N0

3 SINR ANALYSIS AND SELECTION SCHEME  inr

PS hsd

3.1 SINR ANALYSIS

and SINR

 i 1 .

max 

From (2) and (3) the signal to interference and noise ratio for ith relay link can be written as:

ri d

3.2 MAX RELAY SELECTION ANALYSIS

max Pr

hr d

For source ith relay link we use Selection combiner (SC), since
SC make processing for one of the diversity branches that

 SINR  L



i i

ri rid 0

(4)

has the highest SINR. Consider the combiner works under
Rayleigh fading with an i.i.d branches. Therefore the

P h  N

i 1

instantaneous SINR for i branch has the following pdf:

max 

ri d

(5)

1 

 inr  1

i 1

Where  represent the SNR of the ith relay link, and 

inr

p 

SINR   e

 i

 e

 SINR 

(9)

is interference to noise ratio (INR) of interference link, (the 1

Where,  i
is the average SINR at every diversity branch, by
in denominator is value of N0
which normalized as unity).
assuming that all branches have the same average SINR
For analytical tractability in deriving the distribution in (5)
then, the received SINR at the combiner can be written as[16,

at high signal to noise ratio  SNR  

the one in
17]:

 sc  max  i  max  0 , 1 ,..., L1

(10)

denominator of relays link is ignored and thus (5)
approximated to:

max 

Therefore assuming that the channels are independent and identically distributed, we can express the cumulative density function (CDF) of  sc as:

  ri d

 inr

(6)

  

,2 ,..,L

SINR L

i 1

F x

 P max 

 

i1

(11)

N N

Pr hr d

  P  i      F sc

i 1

 

  max

i i = max 

(7)

Where,  

SINR L 2 i

F x represent the CDF of  .

 ri

rid 0

According to our system,

 is an exponential random

P h

i 1

P h

variable. So its CDF can be:



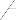
Where  i  L

ri d

F  x   1  e  i

(12)

 ri

rid 0

Equation (12) is also an outage probability for i branch.

P h

i 1

 will

By making use of maximum ratio combining (MRC) technique, the transmitted signals from the source and that one from the best selected relay will be detected at the receiver.
Consequently substituting (12) into (10), the CDF of sc
be:

 i   s   SINR

(8)

Where  S
and

 SINR

are SNR of direct link

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 43

ISSN 2229-5518

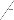
 N

F    1  e 

 1  e SINR N

source relay link can be expressed as:

M 1π

 sc

 

 

 N 

(13)

PSER

 1

TOTAL π

 M 

w M

s sc

w dθ

(19)

     1m e mSINR

m0  m 

Substituting the different moment generating functions by their values, hence the resulting expression will be:

M 1π

Where

  

when all branches are equal, and

P  1

N  N  m 1

m 1

a  b  dθ

(20)

 N 

   N !m! N  m!

 m 

represent the binomial

SER

TOTAL

 

π m 1  m  0

coefficient. By differentiating (13) with respect to  we can



Where a 

sin θ

 

, b 

sin θ 

and

x  b ,

obtain the following pdf:

 N 1 

y  b

2 2

 sin2 θ  x   m sin2 θ  y 

dF  

sc  f

   N 1  e   e 

mSINR

d   sc

N  N 

 

  

(14)

The expression in (20) represents the obtained SER from relay selection and can be calculated by using some partial
fraction expansions as:

  mSINR  

 1m1 e mSINR

P  1

N  N  m 1

1

A Q x

 B Q y

(21)

m1

 m 

SER 

  

 m  

m  m 

The average SNR of the combiner from (13) can be written as
follows[18, 19]:



TOTAL

Where,

π m 1  m 

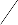
Am  x x  y

, Bm  1 Am

 sc

   f

 sc

  d

(15)

And:

Q c  

4 MGF AND SER PERFORMANCES

ANALYSIS

 M 1 π

1 M



 sin 2 θ 

 M 1π

1 M 



dθ 

  dθ=

  dθ

(22)

MGF is a random variable that gives an alternative method
of representing a PDF through a specific function of a single

 0  sin

θ  c 

 0     cos 

  2 M 1 π M

variable [20]. Using the definition of the MGF, we can define

 2c

   tan 1 

   tan  

 

 sc

given by equation (14) as:

    

  

   

2   0

M SINR

 w 



 e w f

 sc

  d

(16)

Where,   1 2c and   1
Proof: see appendix.
So substituting equation (14) into equation (16) and computing the above mentioned integral we finally obtain the expression of the moment generating function for the best relay as follows:

N  N   

5 SIMULATION RESULTS

Within this section, we present numerical proof that

M sc

 w 

 m 1m 1 SINR



(17)

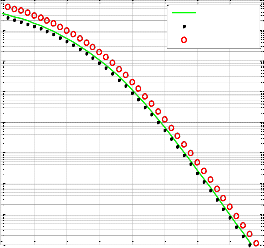
confirms simulation results. Fig. 2 shows the representation

m1  m 

w SINR

of symbol error rate using QPK modulation for analytical
From the above formulation a conditional closed model expression for the SER with M-PSK modulation is
and simulation curves compared with best relay when no
interference as we did in [22] when the number of relays and
mentioned as follows[21]:

M 1π

interferences equal to 2 and the SINR  5
it can been seen

1 M 

b 

that the result between the curves are closely matched,

PSER 

 MGFγ  sin 2 θ  dθ

(18)

additionally, we can easily conclude that SINR based on best

0  

Using equation (18), the total SER from relay selection and
relay demonstrates visible gain over best relay based no
interferences. Taking into consideration the information is

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 44

ISSN 2229-5518

usually transferred through best relay selection path using
DF and the direct link.

Simulation (with)

-1 Analytical(with)

without

-2

-3

-4

-5

-6

This work analyzed the performances of a cooperative communication networks by considering the effect of interference then we compare it with the case of no interferences. The best relay selection using DF protocol is considered. After selecting the best relay using selection combiner (SC) that maximizes received SINR form source- relay link, a maximal ratio combiner (MRC) is used to combine best relay signal and the signal from the direct link. Through statistical analyses, we derived the expression of the received SINR at the destination and established a closed-form expression for the symbol error probability of the system under studied.

Acknowledgements

This work is sponsored by National Natural Science

-7

-8

SNR [dB]

 M 1 π

Fig. 2. SER performance comparison between scheme with/without

1 M 

sin 2 θ 

interference, simulation and best relay using QPSK modulation for number of relays (N=2)

Q c  



  dθ

0  sin θ  c 

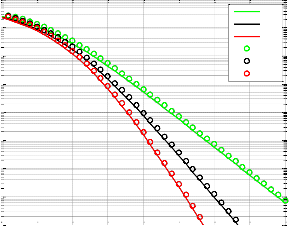
In fig. 3 it presented that increasing number of relays,

 M 1 π

1 M  c 

(23)

reduces significantly the SER for different number of relays and interferences (N=L=1, 2 and 3). Fig. 4 shows the SER of simulation and analytical curves with different interference

  1  sin 2 θ  c  dθ

M 1π

power

 1 

2c  dθ

 

0 1  cos 2θ  2c

N=1

-1 N=2

N=3

-2 N=1

2 M 1π

c M

= 

 1 

  dθ

(24)

N=2

N=3

-3

-4

References

 0  1  2c  cos θ 

-5

-6

-7

-8

0 5 10 15 20 25 30 35 40

SNR [dB]

Fig. 3. Representation of SER versus SNR with (N=L=1, 2and3) relays using QPSK.

6 CONCLUSION

[1] A. Sendonaris, E. Erkip, and B. Aazhang, "User cooperation diversity. Part I. System description," Communications, IEEE Transactions on, vol. 51, pp. 1927-1938, 2003.

[2] T. Cover and A. E. Gamal, "Capacity theorems for the relay

channel," Information Theory, IEEE Transactions on, vol. 25, pp. 572-584, 1979.

[3] J. N. Laneman, D. N. Tse, and G. W. Wornell, "Cooperative diversity in wireless networks: Efficient protocols and outage behavior," Information Theory, IEEE Transactions on, vol. 50, pp. 3062-3080, 2004.

[4] E. E. B. Adam, D. Samb, and L. Yu, "Performance analysis of optimal power allocation in wireless cooperative communication systems," in 2012 International Conference on Graphic and Image Processing, 2013, pp. 87687U-87687U-6.

[5] A. Bletsas, A. Khisti, D. P. Reed, and A. Lippman, "A simple cooperative diversity method based on network path

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 45

ISSN 2229-5518

selection,” vol. 24, ed: IEEE, 2006, pp. 659-672.

[6] F. Yang, M. Huang, M. Zhao, S. Zhang, and W. Zhou, "Cooperative Strategies for Wireless Relay Networks with Co-Channel Interference over Time-Correlated Fading Channels," 2013.

[7] A. M. Salhab, F. Al-Qahtani, S. A. Zummo, and H. Alnuweiri, "Outage Analysis of N^{th}-Best DF Relay Systems in the Presence of CCI over Rayleigh Fading Channels," Communications Letters, IEEE, vol. 17, pp. 697-700, 2013.

[8] N. Wu and H. Li, "Performance Analysis of SNR-based Decode-and-Forward Opportunistic Relaying in the Presence of Co-Channel Interference," Vehicular Technology, IEEE Transactions on, vol. PP, pp. 1-1, 2013.

[9] K. Bakanoglu, E. Erkip, O. Simeone, and S. Shitz, "Relay channel with orthogonal components and structured interference known at the source," 2012.

[10] M. Xia and S. Aïssa, "Cooperative AF relaying in spectrum- sharing systems: performance analysis under average interference power constraints and Nakagami-m fading," Communications, IEEE Transactions on, vol. 60, pp. 1523-

1533, 2012.

[11] S.-I. Kim, S. Kim, J. T. Kim, and J. Heo, "Opportunistic decode- and-forward relaying with interferences at relays," Wireless Personal Communications, vol. 68, pp. 247-264, 2013.

[12] J. Si, Z. Li, and Z. Liu, "Threshold based relay selection protocol for wireless relay networks with interference," in Communications (ICC), 2010 IEEE International Conference on, 2010, pp. 1-5.

[13] I. Krikidis, J. Thompson, S. McLaughlin, and N. Goertz, "Max- min relay selection for legacy amplify-and-forward systems with interference," Wireless Communications, IEEE Transactions on, vol. 8, pp. 3016-3027, 2009.

[14] H. Xu, L. Huang, W. Gang, T. Xu, and Y. Zhang, "Interference- Aware Relay Assignment for Cooperative Networks," in Communication Networks and Services Research Conference (CNSR), 2010 Eighth Annual, 2010, pp. 124-129.

[15] K. T. Truong, P. Sartori, and R. W. Heath, "Cooperative

Algorithms for MIMO Amplify-and-Forward Relay Networks," Signal Processing, IEEE Transactions on, vol. 61, pp. 1272-1287, 2013.

[16] A. Lioumpas, G. Karagiannidis, and T. Tsiftsis, "Adaptive generalized selection combining (A-GSC) receivers," Wireless Communications, IEEE Transactions on, vol. 7, pp. 5214-5219,

2008.

[17] M. Selvaraj and R. Mallik, "Performance of Full CSI Selection

Combining for Cooperative Diversity Systems," 2012.

[18] R. Annavajjala and L. B. Milstein, "Performance analysis of optimum and suboptimum selection diversity schemes on Rayleigh fading channels with imperfect channel estimates," vol. 56, ed: IEEE, 2007, pp. 1119-1130.

[19] T. T. Duy and H.-Y. Kong, "Cooperative Communication with Different Combining Techniques in One-Dimensional Random Networks," networks, vol. 3, p. 4.

[20] J. H. Curtiss, "A note on the theory of moment generating functions,” vol. 13, ed: JSTOR, 1942, pp. 430-433.

[21] E. E. B. Adam, L. Yu, D. Samb, and D. Wang, "Best Relaying

Protocol Selection for Cooperative Networks," in IEEE 14th International Conference on Communication Technology (ICCT) Chengdu, 2012, pp. 104-108.

[22] A. H. M. Hassan, B. Dai, B. Huang, E. Eisa, and M. Azhar, "Relay selection for multiple access relay channel with decode-forward and analog network coding," International Journal of Distributed and Parallel Systems (IJDPS), vol. 3,

2012 2012.

Edriss E. B. ADAM was born in Sinnar state, Sudan, in 1978. He received his M.Sc. degree in Electronics and Information Engineering from Sudan University of Science and Technology, Sudan, in 2008. He is currently working toward Ph.D. degree in Department of Electronics and Information engineering in Huazhong University of Science and Technology, China. His current research interests are in the areas of cooperative wireless communications, and MIMO systems.

Li Yu received her BS, MS, Ph.D. degree in Electronic and Information

Engineering from Huazhong University of Science and Technology in 1992,

1995, and 1999 respectively. She is now the dean of Division of Communication

and Intelligent Network, Wuhan National Laboratory of Optoelectronic. She is

also a chief member of AVS group. Prof. YU was awarded the University Key

Teachers from the Ministry of Education of China, and joined in the New

Century Excellent Researcher Program of China. She has also supervised more

than 30 graduate students in her career as well. Her research focuses on

Multimedia, Wireless Net-work, Video Coding/Decoding and many other

related areas.

Rabiu HARUNA was born in Kano State, Nigeria, in 1977. He is currently M.Sc. candidate at the School of Electronic and Information (EI), Huazhong University of Science and Technology Wuhan, Hubei, P.R. China. His research interest is mainly focuses on wireless Communi-cations and Networking, include cognitive radio. He is a graduate Student member of the IEEE and member of IET.