International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 93
ISSN 2229-5518
Performance Evaluation of Proportional Navigation Guidance for Low-Maneuvering Targets
K. David Solomon Raj, Lecturer, Dept. of Avionics, JNTUK-Kakinada, k.rajusolomon@gmail.com
Abstract— A missile system employed with homing guidance can sense and detect the target, guide itself to steer towards the target by generating commands to its own control surfaces. Proportional Navigation (PN) as an effective guidance law is implemented in most of all the homing guidance systems. Since its inception PN is one of the best proven techniques which has been used extensively in past and present homing systems. This paper presents overall survey of the performance evaluation of the Proportional Navigation which is very effective for the missile to intercept the low-maneuvering target. Here two simulation examples are presented. In the first one, even though if the missile is launched in the wrong direction by a heading error of 50 deg, the PN can enable missile to hit the target. The second is to observe how PN was effective to hit a maneuvering target. Also it is explained why linearization of engagement model results in performance projections with consistent accuracy to make it worthwhile for developing design relationships. In order to show how Proportional Navigation work fairly well against maneuvering and constant velocity target, this paper presents a simulation of a two-dimensional missile target engagement geometry in LabVIEW for a point mass missile and target.
Index Terms— Proportional Navigation, Line-of-sight, Heading Error.
1 INTRODUCTION
—————————— ——————————
For a short-to-medium range homing missiles Proportional Navigation (PN) is perhaps the most widely known and used guidance law. A classical proportional
navigation simply states if two bodies are closing on each other eventually they will intercept when there is no rotation in the line of sight (LOS) between the two bodies relative to the inertial space. By making the interceptor missile heading proportional to the LOS rate for a non maneuvering target the PN guidance law seeks to null out the LOS rate. The relation can be expressed as follows:
an = NVc (dλ/dt) (1)
equations representing the proportional navigation consider the missile-target engagement geometry given by Fig. 1.
Where
an = commanded normal acceleration [ft/sec2] or
[m/sec2]
N = effective navigation ratio
Vc = closing velocity [ft/sec] or [m/sec]
dλ/dt = LOS rate measured by the missile seeker [rad/sec] Depending upon the target maneuver and other system-induced tracking errors the navigation constant (N)
will vary based on the missile acceleration requirements.
The values on N between 3 and 5 are usually used in
order to obtain acceptable miss distance intercept and to
minimize the missile acceleration requirement. An onboard seeker is used to measure the line-of-sight angle with respect to fixed space coordinates there by a lateral (or normal) acceleration of the missile is commanded proportional to that line-of-sight rate. To derive the
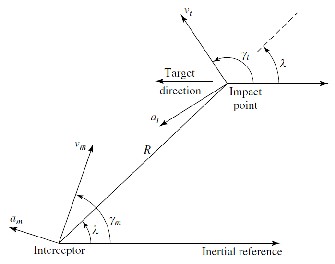
Fig. 1. Interceptor-Target Geometry
During the missile time of flight the missile and target speed is assumed to remain constant. From the Fig. 1 let R be the range between the missile and the target, λ is the line of sight angle rotated from the initial value. Let vm and vt be the interceptor velocity and velocity of the target. In the same way let γm and γt are the missile flight path (or heading) angle and target flight path angle. Also
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 94
ISSN 2229-5518
at any time the difference in the normal components of velocity of the target and missile is the rate of rotation of the line of sight and it can be expressed by the equation
R (dλ/dt) = vt sin(γt - λ) - vm sin(γm - λ) (2) While the velocity component along the line if sight is
given by
the guidance commands with the missile velocity and
seeker gimbal angle (γm – λ).
Now consider non maneuvering target as a special case the LOS rate dλ/dt will be investigated by introducing the range R in Eq. 7 from the operator



𝑑 = � 𝑑 � �𝑑𝑅� (11)
(dR/dt) = vt cos(γt - λ) - vm cos(γm - λ) (3)
𝑑𝑡
𝑑𝑅
𝑑𝑡
At this point by using above operator Eq. 7 becomes
The basic differential equation governing the fact that the
𝑑𝑅
𝑑𝜆
rate of change of the missile heading γm is directly proportional to the rate of change of line-of-sight angle λ is given by
d γm /dt = N(d λ/dt) (4)
where N is the navigation constant. The complete equations of motion for the system are represented by


𝑅 � � � � + 𝜆[2𝑅 + Nvm cos(γm – λ)] = 𝛾Rt vt cos(γt – λ) (12)
𝑑𝑡 𝑑𝑅
Also from Eq. 8
𝑁′ (dR/dt) = - Nvm cos(γm – λ)
Now Eq. 12 takes the form

R�𝑑𝜆� + 𝜆(2 − 𝑁′ ) = 𝛾 (v /R) cos(γ – λ) (13)
equations 2, 3 and 4. Therefore R, γm and λ, the velocities
vm , vt are dependent variables and the target’s flight path
𝑑𝑡
Upon substituting
Rt t t
angle γt must be known or assumed. Here the usual way
ξ = ln(R /R) = -ln(R/R ) (14)
0 0
of implementing a proportional navigation guidance
system is to use the target tracker (or seeker) to measure the line-of-sight rate (dλ/dt). By differentiating the equation 2 the general form of proportional navigation can be developed and is given by
𝑅𝜆 + 𝑅𝜆 = γt vt cos(γt – λ) – 𝛾Rm vm cos(γm – λ) – 𝜆vt C -
with R=R0 (launch) corresponding to ξ = 0 and R=0
(intercept) corresponding to ξ = ∞. Using these one can obtain
dξ = - (R0 /R)(dR/R0 ) and d/dR = -(1/R)(d/dξ)
With these considerations Eq. 13 becomes
d𝜆/dξ + 𝜆�𝑁′ − 2� = - 𝛾 (v /𝑅) cos(γ – λ) (15)
Rt t t
vm cos(γm – λ) (5)
Substituting Eq. 3 and Eq. 4 in Eq. 5 we get
If the target is flying on a straight-line course, then d𝛾Rt /dt
= 0 and the equation 15 takes the form
(2−𝑁′)ξ
2𝑅𝜆 + 𝑅𝜆 = 𝛾Rt cos(γt – λ) – N𝜆vm cos(γm – λ) or (6)
𝜆(ξ) = 𝜆R0𝑒
(16)

𝜆 + �𝜆 � [2𝑅 + N v
cos(γ
– λ)] = (1/R) 𝛾
v cos(γ – λ) (7)
Substituting Eq. 14 into Eq. 16 yields
m m Rt t t
𝑅
(𝑁′−2)
From the above derivation the system equation
𝜆(R/R0 ) = 𝜆R0 (R/R0 ) 𝑒
(17)
consists of Eq. 3, Eq. 4 and Eq. 5. By investigating the special case where by the target flies a straight line-course
From Eq. 17 it can infer that this differential equation
tends to zero for the interceptor-target closing, i.e.
′
that is dγt /dt = 0, we have the inequality
(dR(t)/dt)<0. When 𝑁
= 2, dλ/dt is constant during the
flight and a constant target maneuver is required.
′
𝑁′ = - N {(vm cos(γm – λ))/(dR/dt)} (8)
For 𝑁
> 2, the acceleration required at intercept is zero
Where N’ is commonly called as effective navigation ratio,
and missile’s closing velocity is –dR/dt = vc . From Eq. 7
we can observe that R→0, (dλ/dt) →0 when 𝑑2 𝜆/𝑑𝑡2
remains finite. Now defining the missile normal
which is a highly desirable situation that provides full
maneuvering capabilities of the missile at the intercept
and this can be achieved by giving early corrections to the heading error. At the beginning of the flight, dλ/dt is
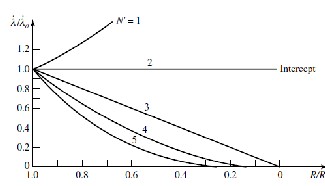
maximum and for 𝑁′ = 3 it decreased linearly to zero and
′
acceleration an as
for 𝑁
> 3 the value reaches to zero asymptotically. At
an = vm (dγm /dt) (9) Where dγm /dt is the missile turning rate. Now
the final (or intercept) point R=0 the collision course
condition dλ(t)/dt = 0 can be achieved with a vanishing
turning rate dγm /dt =0. If we assume the target is flying
from left to right then the plot of (𝜆/𝜆R0 ) vs. (R/R0 ) is shown
substituting Eq. 4and Eq. 8 in Eq. 9 we observe
𝑑𝜆
𝑑𝜆
by Fig. 2

an = {-N𝑅vm / vm cos(γm – λ)}(
(10)
𝑑𝑡

) = {Nvc /cos(γm – λ)}(
);
𝑑𝑡
Equation 10 is the well-known general classical proportional navigation guidance and is used to generate
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 95
ISSN 2229-5518
Considering the missile course is from left to right we can observe from Fig. 3 largest acceleration occurs at the end if the flight. The Fig. 3 depicts the fact that anm grows
beyond all limits for 𝑁′ = 2 . For evaluating Eq. 22 a special case where𝑁′ = 2 , the following transformation
will be applied by transforming the expression (𝑅/𝑅R 0 )
into
𝑎𝑥 = 1 +
𝑙𝑛 𝑎

+
1!

(ln 𝑎)2
2!
𝑥2 + ⋯ (23)
N’-2
Fig.2 Plot of ( 𝜆 / 𝜆R 0 ) vs. (R/R0 ) with 𝑁′ as a non
Eq. 22 can be obtained in the form
2
maneuvering target parameter.
|𝑎𝑛𝑚 /𝑎𝑛𝑡 | = 𝑁′ �−

�ln� 𝑅 ��

𝑅0 −
1!

�ln� 𝑅 ��

𝑅0
2!
� �𝑁′ − 2� − ⋯ (24)
Now consider the maneuvering target, while estimating
LOS rate dλ/dt, the right-hand side of Eq. 15 remains

Also for 𝑁′ = 2
|𝑎𝑛𝑚 /𝑎𝑛𝑡 | ≈ −2ln(
) (25)
constant. The solution of Eq. 15 is given by
𝑑𝜆 ′
𝑅0
From Eq. 25 one can understand that as R→0 the

(
𝑑𝑡
) = (γt vt cos(γt – λ)/𝑅(2 − 𝑁′)){1- 𝑒−(𝑁 −2)ξ} (18)
missile acceleration a
nm →∞. From the above analysis we
For eliminating ξ substitute Eq. 14 in Eq. 18 and one
can obtain
𝑑𝜆
can summarize a launch heading error correction by
means of proportional navigation utilizes minimum
effective navigation ratio of 2 (i.e 𝑁′ = 2). Also during the

(
𝑑𝑡
) = ( γt vt cos(γt – λ)/𝑅(2 − 𝑁′)){1- (𝑅/𝑅R 0 )
(19)
terminal portion of the flight the missile maneuvers are at
The ratio of interceptor missile’s normal (or lateral)
acceleration to the target’s lateral acceleration is given by
|𝑎𝑛𝑚 /𝑎𝑛𝑡 | = |𝑣𝑚 𝛾𝑚 /𝑣𝑡 𝛾𝑡 | = (vm /vt ) N (λ/γt ) (20)
Using the ratio k as vm /vt and Eq. 19, Eq. 20 can be written
as
|𝑎𝑛𝑚 /𝑎𝑛𝑡 | = (𝑁′ /(𝑁′ − 2))|𝑐𝑜𝑠(𝛾𝑡 − 𝜆)/cos(𝛾𝑚 − 𝜆)| {1-
reasonable level where at the earlier in flight the collision
course errors are corrected for 𝑁′ > 3.
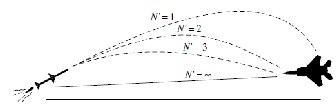
For various values of effective navigation ratio the
family of homing missile trajectories at fixed launching
errors is shown by Fig 4. Finally we can conclude as 𝑁′
increases: heading error decreases, initial acceleration
required by the missile is high and acceleration required at the terminal-phase to intercept the target is reduced.
(𝑅/𝑅R 0 )
N’-2} (21)
Making the use of approximation regardless of direction
of approach to the target |𝑐𝑜𝑠(𝛾𝑡 − 𝜆)/cos(𝛾𝑚 − 𝜆)|≈1, we
can obtain
|𝑎𝑛𝑚 /𝑎𝑛𝑡 | ≈ (𝑁′ /(𝑁′ − 2){1- (𝑅/𝑅 0 ) N’-2} (22)
For a maneuvering target with 𝑁′ as a parameter the ratio of |𝑎𝑛𝑚 /𝑎𝑛𝑡 | with respect to the relative distance to the
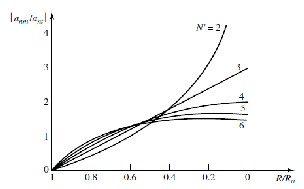
target (R/R0 ) is shown by Fig. 3
Fig. 3 Plot of |𝑎𝑛𝑚 /𝑎𝑛𝑡 | vs (R/R0 ) for a maneuvering target.
Fig. 4. 𝑁′ Effecting various missile flight.
2 TWO-DIMENSIONAL MISSILE-
TARGET ENGAGEMENT GEOMETRY
The previous section dealt with the theoretical side of proportional navigation and to understand better the working of proportional navigation. Consider point mass missile-target engagement geometry in two dimensional as shown in the Fig. 5.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 96
ISSN 2229-5518
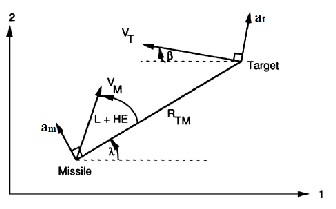
Fig. 5 Two-dimensional missile-target engagement geometry
For simulating this model both missile and target are assumed to travel at constant velocity. From Fig. 5 missile is heading at an angle of L + HE with velocity magnitude vm with respect to line of sight. Here L is the missile lead angle and theoretically it is the correct angle for the missile to be on a collision triangle and angle HE is known as heading error. Line of sight is the imaginary line connecting the missile and target which makes an angle λ with respect to fixed reference and let RTM be the instantaneous separation between missile and the target. In this simulation we desire to make RTM as small as possible at the expected intercept point. The closest approach point between the missile and the target is known as the miss distance. In this engagement model let at be the acceleration magnitude of the target which can maneuver evasively. Also we can express angular velocity of the target as
maneuver and heading error which are considered as two error sources.
The integration step size for most of the flight is fixed i.e. H=0.01 s and to accurately capture the magnitude of the miss distance the integration step size is made smaller near the end of the flight (H=0.0002 s when RTM <1000ft). The program is terminated when the separation between the target and the missile is minimum, which means closing velocity changes its sign. In order to observe how effective in increasing the navigation ratio causes heading error to be removed more rapidly, a sample case was simulated where the only form of disturbance was a 50- deg Heading error (HEDEG = -50). Fig. 6 shows the
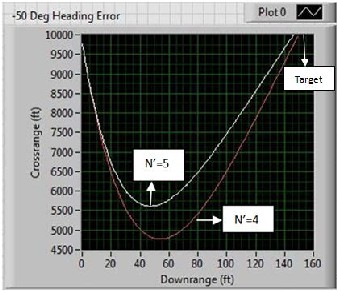
sample trajectories for 𝑁′ = 4 𝑎𝑛𝑑 5.

𝛽 = 𝑎𝑇
𝑣𝑇
2.1 SIMULATION OF TWO-
DIMENSIONAL PROPORTIONAL
(26)
𝑁′
Fig. 6. Initial removing of Heading Error by increasing
From Fig.6 we can observe because of heading error
NAVIGATION
The differential equations governing a complete missile-target engagement model represented by Fig. 5 in two dimensions can be found in [7]. Any homing missile incorporated with proportional navigation guidance is not fired at the target but it is fired in a direction to intercept the target. Under a variety of circumstances it is better to simulate and test the properties of guidance algorithm to witness and understand the insight of proportional navigation. Here the initial location of the missile and the target, flight time, speeds and effective navigation ratio are the simulation inputs and the user can vary target
the missile is flying initially in a wrong direction and consequently the guidance law is forcing the missile to home on the target. A much tighter trajectory can be established with larger effective navigation ratio which removes the initial heading error more rapidly by the
missile. At two different instants 𝑁′ = 4 𝑎𝑛𝑑 5.
proportional navigation guidance law proves that the
missile hit the target near zero miss distance. Fig. 7 shows how by increasing the effective navigation ratio can cause more acceleration.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 97
ISSN 2229-5518
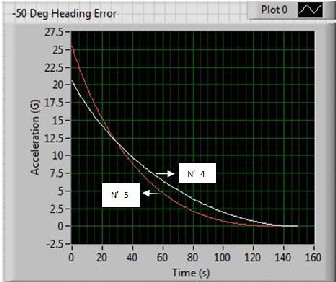
Fig. 7. Higher acceleration at the beginning of flight for
different values of 𝑁′
From the Fig. 7 at two different instants the time
histories of missile acceleration are somewhat different.
The quicker removal of the initial heading error at 𝑁′ = 5
results in larger acceleration of the missile at the
beginning of the flight and lower accelerations at the end of the flight. In both the situations the missile acceleration
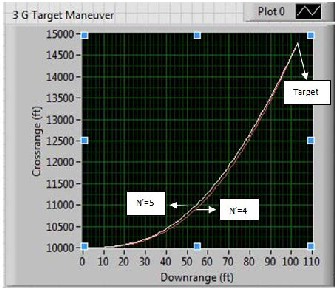
Fig. 8. Against Maneuvering Target
to hit the target and to remove the heading error is monotonically decreasing and becoming zero at the end of the flight. Indeed one of the principles of proportional navigation guidance is to remove the heading error as soon as possible throughout the entire flight. Thus by increasing the effective navigation ratio the missile can take out the initial heading error more rapidly.
In previous simulation analysis the only disturbances was heading error. Now another sample case was run where the only form of disturbance was a 3-g target
maneuver. In this case initially the missile and the target are on a collision triangle. Here the target velocity vector is along the line of sight initially and also all of 3 g target acceleration is perpendicular to line of sight. Due to rapid turning of the target the magnitude of the target acceleration which is perpendicular to line of sight diminishes. The simulation results for these missile-target trajectories with effective navigation ratios of 4 and 5are shown in Fig. 8.
We can see from the Fig. 8, a value of 𝑁′ = 5 can lead
the missile to intercept the target slightly more than the
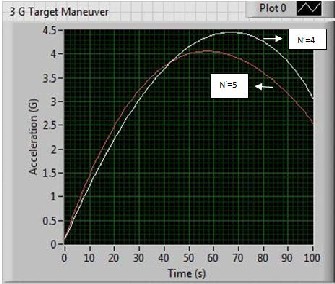
lower effective navigation ratio and that differentiate the two trajectories. However in both the cases, proportional navigation guidance law can enable the missile to intercept the maneuvering target.
Fig. 9. Higher the 𝑁′ the less acceleration to hit the target
Fig. 9 depicts the fact that there are significant
differences between the maneuvering target acceleration
profiles. Even though both acceleration profiles are
monotonically increasing, the larger effective navigation ratio causes less acceleration for the missile.
3. LINEARIZATION
In the previous analysis the effectiveness of proportional navigation has been understood from numerical simulation results of two-dimensional engagement simulation. Now in this section to gain more understanding we will linearize the two-dimensional engagement model by defining some relative quantities as shown in Fig. 10.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 98
ISSN 2229-5518
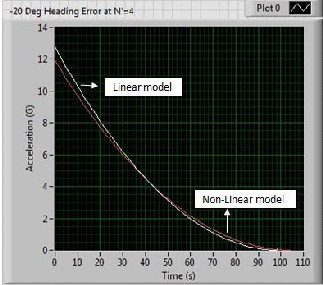
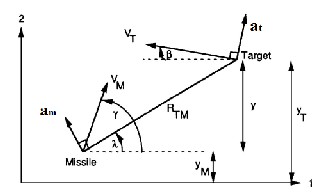
Fig. 10. Intercept model for Linearization.
From the Fig. 10 the difference between missile and
the target acceleration which is called relative acceleration
can be written as
𝑦 = 𝑎𝑡 𝑐𝑜𝑠𝛽 − 𝑎𝑐 𝑐𝑜𝑠𝜆 (27)
If the cosine terms are approximately unity means if
the flight path angles are small the preceding equation can
be written as
𝑦 = 𝑎𝑡 − 𝑎𝑐 (28)
Using small-angle approximation the line of sight
angle can be yielded as
Fig. 11. Comparison of Acceleration Profiles with heading error disturbance
From the Fig. 11 it is clearly understood that resultant acceleration profiles for both models are virtually

𝜆 = 𝑦
𝑅𝑇𝑀
(29)
indistinguishable even for relatively large heading error
disturbance.
Closing velocity for a head on case and tail chase case
can be approximated as
𝑉𝐶 = 𝑉𝑀 + 𝑉𝑇 (30)
𝑉𝐶 = 𝑉𝑀 − 𝑉𝑇 (31)
With the time varying relationship the range equation
can be written as
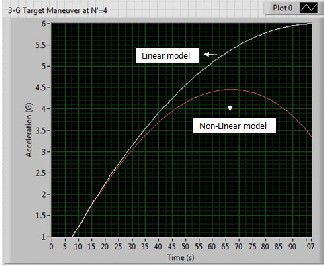
Another linear engagement model simulation was run for a sample case with a 3-g target maneuver and was shown in Fig. 12.
𝑅𝑇𝑀 = 𝑉𝐶 (𝑡𝐹 − 𝑡) (32)
Where t and tF are the current time and total time of
flight of the engagement.
The relative separation between missile and the target y at the end of the flight is taken to be miss distance and is given by
𝑀𝑖𝑠𝑠 = 𝑦(𝑡) (33)
3.1 LINEARIZED ENGAGEMENT
SIMULATION
After developing the linearized equations for the missile-target geometry the simulation for this engagement will be done in this section to see if the
resultant linearized equations give performance projections which are similar to those of nonlinear engagement equations. In simulating the linearized proportional navigation engagement the tF is the input instead of output.
To verify the model as a reasonable approximation to the nonlinear engagement model, a sample run was made with the only disturbance was a -50-deg heading error. The effective navigation ratio for this case is 4 and the acceleration profiles for both linearized as well as non- linearized engagement models are shown by Fig. 11.
Fig. 12. Comparison of Acceleration Profiles for a 3-g target maneuver.
The discrepancy in the Fig. 12 is that the linear model assumes the magnitude of the target acceleration perpendicular to the line of sight is same and equal to the magnitude of the maneuver. Also the linear model overestimates the missile acceleration due to target maneuver. In reality the component of the acceleration perpendicular to the line of sight decreases because the target is turning. From this analysis its understood that
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 99
ISSN 2229-5518
the nonlinear acceleration requirements due to maneuvering target are less than those predicted by the linearized engagement model.
4. CONCLUSION
From the previous simulation results the effectiveness of proportional navigation guidance is very efficient to hit a target even if the missile is launched in wrong direction by 50 deg. Also the guidance law worked for a maneuvering target. In both analyses it requires a certain acceleration levels for a missile to hit a target. They rely on the type of error source and especially on effective navigation ratio. If the missile is not having sufficient acceleration generated by the guidance law, a miss will result. Finally the method of linearization is found to yield performance projections of sufficient accuracy thereby the design relationships can be verified and tested.
REFERENCES
[1]. Zhou Weiwen ; Liang Xiaogeng ; Jia Xiaohong, “Finite-time stability analysis of proportional navigation guidance system”, IEEE Trans, ICIS, Vol. 1, Pages: 108-

112, 2010.
[2]. Viswanath D. ; Deb D. “A new non linear guidance

law formulation for proportional navigation
guidance”, IEEE Trans, VSS, and Pages: 190-195, 2012.
[3] Seunghyun Kim ; Kim, H.J. “Robust Proportional
Navigation Guidance against highly maneuvering

targets”, IEEE Trans, ICCAS, and Pages: 61-65, 2013
[4]. Kumar, A. ; Ojha, A., “Performance evaluation of
certain proportional navigation schemes”, IEEE Trans,

CARE, Pages: 1-17, 2013.
[5] Dhananjay, N. ; Kai-Yew Lum ; Jian-Xin Xu,
“Proportional Navigation with Delayed Line-of-sight”, IEEE Trans on CST, Vol. 21, Pages: 247-253, 2013.
[6]. George M. Siouris, “Missile Guidance and Control
System”, New York: Springer, 2004.
[7]. Paul Zarchan., “Tactical and Strategic Missile
Guidance”, AIAA, Vol. 239, 2012.
IJSER © 2014 http://www.ijser.org











