International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1376

Performance Analysis of Different LMS Algorithms

for Health Monitoring ECG Sensor

Monpur Ashwin, Chunduri.V.M.Naren Simha

Abstract—In this paper, with the latest advancements in electronics, several techniques are used for removal of unwanted entities from signals especially that are implied in the most sophisticated applications. The removal of power line interference from most sensitive medical monitoring equipment’s can also be removed by implementing various useful techniques with different error nonlinearity-based adaptive filters, which are computationally superior having multiplier free weight update loops are used for cancellation of noise in electrocardiographic (ECG) signals. The proposed implementation is suitable for applications such as biotelemetry, where power line interference (50/60 Hz) is the main source of noise in most of bio-electric signals. These schemes mostly employ simple addition, shift operations and achieve considerable speed up over the other least mean square (LMS)-based realizations. Simulation studies shows that the proposed realization gives better performance compared to existing realizations.

Index Terms—Adaptive-filtering, Convergence of lms algorithms, electrocardiographic (ECG), least mean square (LMS) algorithm, power line interference, noise cancellation, telecaridiology.

.

——————————  ——————————

1 INTRODUCTION

IOTELEMETRY is defined as transmitting biological or physiological data from a remote location to a location that has the capability to interpret the data and affect decision
making. Biotelemetry is an important method for monitoring
physiological variables by providing a wireless link between the subject and the data collection equipment. Biomedical data has been telemetered through every medium between two sites, including air, space, water and biologic tissue, by using a variety of modulated energy forms like electromagnetic waves, light, and ultrasound. One of the applications in biotelemetry is wireless Ambulatory ECG system. In such cases, the ECG signal is used to know the cardiac condition of an ambulatory patient. Wireless Ambulatory ECG recording is now routinely used to detect arrhythmias and cardiac abnormalities. As the ECG signal contains numerous artifacts, these artifacts have to be removed before monitoring, from the receiver point-of-view, so that a correct decision can be taken. So, it is necessary to remove the different artifacts present in the ECG signal hence there is a need of filtering the ECG signal. In a practical case most of the signals are non-stationary and the filter, which we use must change its coefficient according to the input signal.
Several filtering techniques has presented in literature for ECG analysis, which includes, adaptive and non-adaptive techniques [1]–[13], adaptive filtering techniques permit to the detect time varying potentials and to track the dynamic variations of the signals. In [2], Thak or et al. proposed an least mean square (LMS) based adaptive recurrent filter to acquire the impulse response of normal QRS complexes and then applied it for arrhythmia detection in ambulatory ECG
————————————————

 Monpur Ashwin is currently pursuing bachelor’s degree program in electrics and communication engineering in SRM University, India,

 PH-+918801855588. E-monpur_ashwin@srmuniv.edu.in

 Chunduri.V.M.Naren Simha is currently pursuing bachelor’s degree

program in electrics and communication engineering in SRM University,

India, PH-+918015201609. E-naren_simha@srmuniv.edu.in
recordings. . The reference inputs to the LMS algorithm are deterministic functions and are defined by a periodically extended, truncated set of orthonormal basis functions. In such a case, the LMS algorithm operates on an instantaneous basis such that the weight vector is updated for every new sample within the occurrence based on an instantaneous gradient estimate. In a study, however, a steady-state convergence analysis for the LMS algorithm with deterministic reference inputs showed that the steady-state weight vector is biased and thus the adaptive estimate does not approach the Wiener solution [14]. In [15], Kotas presented an application of principal component analysis and its robust form for ECG enhancement, Floris et al. elaborates the fast lane approach using improved versions of LMS and normalized LMS (NLMS) algorithms for the prediction of respiratory motion signals [16], subtraction procedure without affecting the components of ECG signal [17], Sayadi et al. in [18] proposed bionic wavelet trans- form for the correction of baseline drift and Sameni et al. in [19] established a framework of Bayesian filtering for ECG de- noising. Apart from these ECG enhancement techniques several adaptive signal processing techniques are also published, e.g., NLMS algorithm with decreasing step size, which converge to the global minimum [20], a variable step size NLMS algorithm with faster convergence rate [21], Costa et al. in [22] proposed a noise resilient variable step size LMS which is specially indicated for biomedical applications. Also, several modifications are presented in literature to improve the performance of the LMS algorithm [23]. Recently, in [24], Rahman et al. presented several less computational complex adaptive algorithms based on data normalization.
In recent years, biotelemetry has become more important. In [25], Sufi et al. proposed ECG compression algorithms for wireless telecardiology. Complexity reduction of the noise cancellation system, particularly in applications such as wire- less biotelemetry system has been remained a topic of intense research. This is because of the fact that with increase in the ECG data transmission rate, the receiver filter’s impulse response length increases and thus the order of the filter

IJSER © 2014 http://www.ijser.org

International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1377

increases. The resulting increase in complexity makes the real- time operation of the biotelemetry system difficult, especially in view of simultaneous shortening of the symbol period, which means that lesser and lesser time will be available to carry out the computations, while the volume of the computations goes on increasing. Thus far, to the best of the author’s knowledge, no effort has been made to reduce the computational complexity of the adaptive algorithm without affecting the signal quality. The computational complexity can be reduced by using the sign based algorithms, namely, the signed regressed algorithm, the sign algorithm, and the sign-sign algorithm [27], all three require only half as many multiplications as in the LMS algorithm, thus making them attractive from practical implementation point-of-view. In order to cope with both the complexity and convergence issues without any restrictive tradeoff, we propose various adaptive filter structures based on the error nonlinear signed regressed LMS (ENSRLMS) algorithm, the error nonlinear sign LMS (ENSLMS) algorithm, and the error nonlinear sign-sign LMS (ENSSLMS) algorithm. These algorithms enjoy less computational complexity because of the sign present in the algorithm and good filtering capability because of the normalized term [25], [26]. To study the performance of the filter structures which effectively remove the artifacts from
the ECG signal. The simulation results show that the performance of sign-based algorithms is better than the LMS counterpart.

2 COMPUTATIONALLY EFFICIENT ADAPTIVE

FILTERING TECHNIQUES

The electrocardiogram (ECG) is a graphical representation of hearts functionality and is an important tool used for diagnosis of cardiac abnormalities. In the clinical environment during acquisition, the ECG signal encounters various types of artifacts. The predominant artifact in the ECG includes Power- Line Interference (PLI). This artifacts strongly affects the ST segment, degrades the signal quality, frequency resolution, produces large amplitude signals in ECG that can resemble PQRST waveforms, and masks tiny features that are important for clinical monitoring, diagnosis. Cancellation of these artifacts in ECG signals is an important task for better diagnosis. The extraction of high-resolution ECG signals from recordings which are contaminated with background noise is an important issue to investigate. The goal of ECG signal enhancement is to separate the valid signal components from the undesired artifacts and to present an ECG that facilitates easy, accurate interpretation. So, we need to develop efficient adaptive noise cancelers.

Consider a length , LMS-based adaptive filter, depicted in
Fig. 1, that takes an input sequence and updates the
weights as
�(𝑛 + 1) = �(𝑛) + 𝜇�(𝑛)𝒆(𝑛) (1)

Fig. 1. Adaptive filter structure

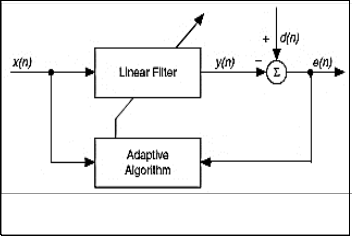
error signal �(𝑛) = �(𝑛) − �𝒕 (𝑛)�(𝑛) , with �(𝑛) being so called the desired response available during initial training period,

and denoting so-called step-size parameter.
In order to remove the noise from the ECG signal, the ECG
signal 𝑠1 (𝑛)corrupted with noise signal 𝑝1 (𝑛) is applied as the desired response �(𝑛) to the adaptive filter shown in Fig. 1. If the noise signal 𝑝2 (𝑛), possibly recorded from another generator of noise that is correlated in some way with 𝑝1 (𝑛) is applied at the input of the filter, i.e., �(𝑛) = 𝑝2 (𝑛) the filter error becomes �(𝑛) = [𝑠1 (𝑛) + 𝑝1 (𝑛)] − �(𝑛) , where �(𝑛) is the filter
output and it is given by
�(𝑛) = � 𝑡 (𝑛)�(𝑛) (2)
Now, the mean-squared error (MSE) becomes
𝐸(� 2) = {𝐸{𝑠1 (𝑛) − �(𝑛)]2} + 𝐸[𝑝2(𝑛)] (3)
Since 𝑠1 (𝑛) and 𝑝1 (𝑛) are uncorrelated, similarly 𝑝1 (𝑛) and
�(𝑛) are uncorrelated and the last two expectations are zero.
Minimizing the MSE results in a filter output which is the best
least squares estimated of the signal 𝑠1 (𝑛) [2[,[31].
New algorithms that make use of the signum (polarity) of
either the error or the input signal, or both [27], have been
derived from the LMS algorithm for the simplicity of
implementation, enabling a significant reduction in computing time, particularly the time required for “multiply and accumulate” (MAC) operations. These algorithms are attractive for their assured convergence and robustness against the disturbances in addition to the ease of implementation. The most important members of this class of algorithms are: Signed regressed Algorithm (SRA), Sign Algorithm (SA), and Sign- Sign Algorithm (SSA). The weight update relations for these algorithms, respectively, are
�(𝑛 + 1) = �(𝑛) + 𝜇𝑠𝑔𝑛{�(𝑛)}{�(𝑛)} (4)
�(𝑛 + 1) = �(𝑛) + 𝜇{�(𝑛)}𝑠𝑔𝑛{�(𝑛)} (5)
Where �(𝑛) = [�0(𝑛)�1(𝑛) … . �𝐿 − 1(n)] ise the tap weight vector at the nth index �(𝑛) = [�(𝑛)�(𝑛 − 1) … . �(𝑛 − 𝐿 + 1)]t,
and
�(𝑛 + 1) = �(𝑛) + 𝜇𝑠𝑔𝑛{�(𝑛)}𝑠𝑔𝑛{�(𝑛)} (6)

IJSER © 2014 http://www.ijser.org

International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1378

Where sgn{ } is the well-known signum function, i.e.
1: �(𝑛) > 0
𝑠𝑔𝑛{�(𝑛)} = { 0: �(𝑛) = 0
−1: �(𝑛) < 0
Among the adaptive algorithms presented above, the SRA, SA,
and SSA has a convergence rate and a steady-state error that are slightly inferior to those of the LMS algorithm for the same parameter setting because of the sign present in the algorithm, i.e., some residual noise present in the signal, but speed up as the mean square error drops. However, the computational complexity of these algorithms is much less compared to the LMS algorithm.
This can be explained as follows. Consider the SA, it may be written as

�(𝑛 + 1) = �(𝑛) + 𝜇{�(𝑛)} { 𝑒(𝑛) } (8)

|𝑒(𝑛)|

Since 𝑠𝑔𝑛[�(𝑛)] = �(𝑛)/|�(𝑛)| :
This is rearranged as

�(𝑛 + 1) = �(𝑛) + [ 𝜇 ] �(𝑛)�(𝑛) (9)

𝑒(𝑛)

The above equation reveals that the sign algorithm may be
thought as an LMS algorithm with a variable step size

Comparing (1) and (10), the update equation of NLMS is a scaled version of LMS algorithm. The size of the change to weight vector is therefore to be inversely proportional to the norm of data vector .
The data vector with a large norm will generally lead to a small change to than a vector with a smaller norm. This normalization results in smaller step size values than the conventional LMS. The normalized algorithm usually converges faster than the LMS algorithm, since it utilizes a variable convergence factor aiming at the minimization of the instantaneous output error [29]. Instead of using the
instantaneous data vector for normalization, the squared norm
of the error vector can be used. The length of the error vector is
the instantaneous number of iterations. Because the step size is normalized with reference to error, this algorithm is called the Error Nonlinear LMS (ENLMS) algorithm. A common major drawback of adaptive noise cancelers using LMS-based algorithms is the large value of excess mean-square error which results in signal distortion in the noise-canceled signal. In the ENLMS algorithm, the time-varying step-size is inversely proportional to the squared norm of error vector rather than the input data vector as in the NLMS algorithm. This algorithm provides significant improvements in decreasing mean- squared error (EMSE) and consequently minimizing signal distortion [28], [29].
The weight update relation for ENLMS algorithm is as follows:

parameter, 𝜇𝑡 = {𝜇/�(𝑛)}. The step size parameter

�(𝑛 + 1) = �(𝑛) + [ 𝜇

] �(𝑛)�(𝑛) (12)

increases, on an average, as the sign algorithm converges, since

decreases in magnitude. A small leads to an equally small

value for in the initial portion of the sign algorithm. As a result the algorithm initially converges slowly. However, as the algorithm converges and becomes smaller in magnitude, the step size becomes larger, leads to a faster convergence. Moreover the sign present in the algorithm and setting to a value of power of two, the hardware implementation is highly simplified (shift and add/subtract operation only) [27].
The NLMS algorithm is another class of adaptive algorithm used to train the coefficients of adaptive filter. This algorithm accounts the variation in signal level at filter output and selecting the normalized step size parameter that results in a stable as well as a fast converging algorithm. The weight update relation for NLMS algorithm is as follows:

𝑝+𝑒 𝑡 (𝑛)𝑒(𝑛)

The variable step can be written as

𝜇 (𝑛) = 𝜇 (13)

𝑝+𝑒 (𝑛)𝑒(𝑛)

The advantage of the ENLMS algorithm is that the step size can

be chosen independent of the input signal power and the number of tap weights. Hence, the ENLMS algorithm has a convergence rate and a steady-state error better than the LMS algorithm. On the other hand, some additional computations are required to compute . In order to cope up with both the complexity and convergence issues without any restrictive tradeoff, we propose error normalized sign based algorithms such as the error nonlinear signed regressed LMS (ENSRLMS) algorithm, the error nonlinear sign LMS (ENSLMS) algorithm, and the error nonlinear sign-sign LMS (ENSSLMS) algorithm

�(𝑛 + 1) = �(𝑛) + [ 𝜇

𝑝+𝑥𝑡 (𝑛)𝑥(𝑛)

The variable step can be written as

𝜇(𝑛) = 𝜇

] �(𝑛)�(𝑛) (10)

(11)
for the removal of noise from ECG signal. The weight update relations for these algorithms, respectively, are
�(𝑛 + 1) = �(𝑛) + 𝜇𝑒 (𝑛) + 𝑠𝑔𝑛{�(𝑛)}{�(𝑛)} (14)
�(𝑛 + 1) = �(𝑛) + 𝜇 (𝑛){�(𝑛)}𝑠𝑔𝑛{�(𝑛)} (15)

𝑝+𝑥𝑡 (𝑛)𝑥(𝑛)

Here, is fixed convergence factor to control maladjustment.

The parameter is set to avoid the denominator being too small and the step size parameter too big.
and

𝑒

�(𝑛 + 1) = �(𝑛) + 𝜇𝑒 (𝑛)𝑠𝑔𝑛{�(𝑛)}𝑠𝑔𝑛{�(𝑛)} (16)

IJSER © 2014 http://www.ijser.org

International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1379

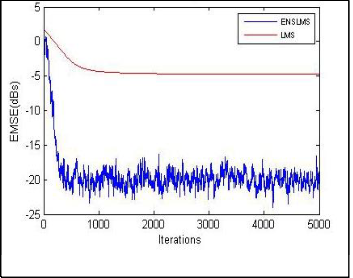
Fig. 2(a). Convergence characteristics of LMS algorithms.

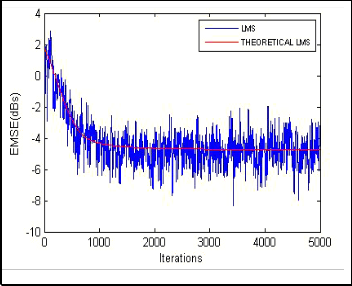
Fig. 2(c). Convergence characteristics of LMS and ENSRLMS algorithms.

2.1 Computational Complexity Issues

As the sign-based algorithms are largely free from the MAC



operations, the proposed schemes provide elegant means to re- move noise from the ECG signal. Table I provides comparative account of different commonly used algorithms and the proposed algorithm in terms of number of operations required. Among all the algorithms the ENLMS is more complex, it re- quires MACs and one division. The conventional LMS algorithm requires MAC operations to implement the weight updating (1) on DSP processor. For the SSLMS algorithm, to evaluate from using (4), only add with sign check (ASC) operations are required. But the rate of convergence of this algorithm is very slow. Hence, the SSLMS algorithm alone will not be a suitable candidate for the removal of noise from the ECG signal. The ENSSLMS algorithm, which is the combination of SSLMS and ENLMS is very much suit-able

as this algorithm requires shift ASC operations in case of block-based realization or if we choose the value of as a power of 2. From Table I, it is also clear that the number

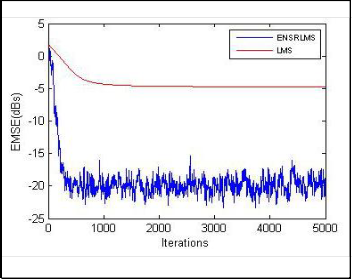
Fig. 2(b). Convergence characteristics of LMS and ENSLMS algorithms

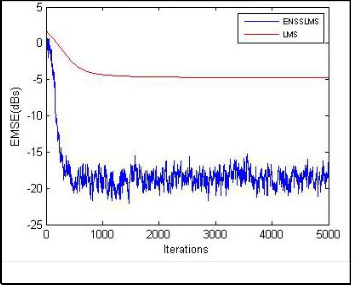
Fig. 2(d). Convergence characteristics of LMS and ENSSLMS algorithms.

utations required for the proposed block-based ENSRLMS is

independent of filter.

TABLE 1

A COMPUTATIONAL COMPLEXITY COMPARSION TABLE

IJSER © 2014 http://www.ijser.org

International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1380

and ENLMS is very much suit-able as this algorithm requires shift ASC operations in case of block-based realization or if we choose the value of as a power of 2. From Table I, it is also clear that the number of computations required for the proposed block-based ENSRLMS is independent of filter length

. Note that ASC and shift operations requires less logic circuitry when compared with MAC operations.

3 SIMULATION RESULTS

To show that error nonlinear signed algorithms are really effective in clinical situations, the method has been validated using ECG recordings. In our simulation, we used the first 5000 samples of the ECG signals. For evaluating the performance of proposed filter structures, we have measured signal-to-noise ratio improvement (SNRI) and compared with the LMS algorithm. For all the figures, a number of samples is taken on axis and amplitude on axis, unless stated. Table II gives the comparison of various algorithms in terms of mean square error (MSE) and excess mean square error (EMSE). Table III gives the contrast of algorithms in terms of SNRI (dBs). Various adaptive filter structures are implemented using LMS, ENSRLMS,
ENSLMS and EN-SSLMS algorithms.

3.1 Noise Generator

The reference signal shown in Fig. 1 is taken from noise generator. A synthetic PLI with 1 mv amplitude is simulated for PLI cancellation, no harmonics are synthesized. This database was recorded at a sampling rate of 50 Hz. The input SNR for the above nonstationary noise is taken as 2dB. In the considered simplified algorithms because of the sign present in the recursion some tiny noise remains along the ST segment of the ECG signal. In order to extract the residual noise, a tiny PLI is added to the noise reference signal. This improves the performance of the filter.
TABLE II

COMPARISON OF MSE AND EMSE OF VARIOUS ALGORITHMS FOR µ=0.005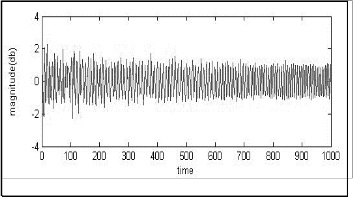

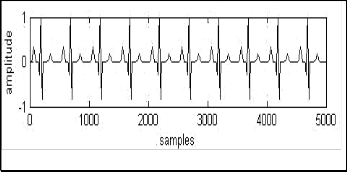
Fig. 3(a) ECG signal

Fig. 3(b) ECG signal and its spectrum

3.2 Adaptive Power-Line Interference Canceler

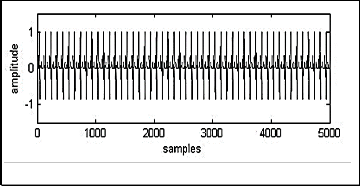
This experiment demonstrates power-line interference (PLI) cancellation. The input to the filter is ECG signal corrupted with a synthetic PLI of frequency 50 Hz and sampled at 200 Hz, which is generated in the noise generator. The reference signal is synthesized PLI, the output of the filter is recovered signal. The simulation results are shown in Fig. 4. The frequency spectrum before filtering and after filtering using the LMS and ENSRLMS algorithms are shown in Fig. 5. The SNR contrast for the dataset is shown in Table III. In SNR measurements, it is found that ENSRLMS algorithm gets SNRF of 12.0636 dB, ENSLMS gets 10.7250 dB, ENSSLMS gets 9.4302 dB, whereas the conventional LMS algorithm gets to 10.2215dB.

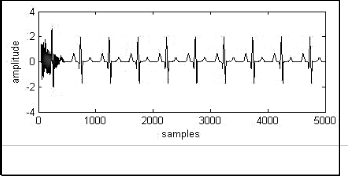
Fig. 4(a). ECG Signal with PLI.

IJSER © 2014 http://www.ijser.org

International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1381

Fig. 4(b). PLI cancelled filtered signal with LMS algorithm.

Fig. 4(c). PLI cancelled filtered signal with ENSSLMS algorithm.

Fig. 4(d). PLI cancelled filtered signal with ENSRLMS algorithm.

Fig. 4(e). PLI cancelled filtered signal with ENSLMS algorithm.

Fig. 5(a). Spectrum of ECG with PLI.

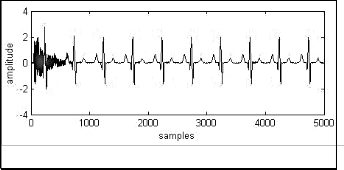
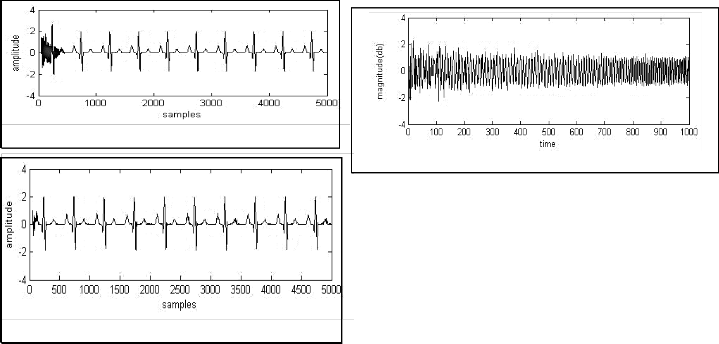
Fig. 5 (b). Spectrum after filtering with LMS algorithm.

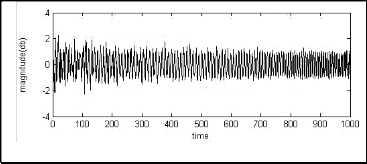
Fig. 5(c) Spectrum after filtering with ENSRLMS algorithm.

TABLE III

PERFORMANCE CONTRAST OF VARIOUS ALGORITHMS FOR THE REMOVAL OF PLI NOISE (ALL VALUES IN (dBs).

4 CONCLUSION

In this paper, the problem of noise cancellation from ECG signal using error normalization based adaptive filters are proposed and tested. For this, the input and the desired response signals are properly chosen in such a way that the filter output is the best least squared estimate of the original ECG signal. Among the three algorithms, ENSRLMS performs better than the other. From the simulated results, it is clear that these algorithms remove the artifacts efficiently present in the ECG signal. The proposed treatment provides high SNR with less computational complexity. The computational complexity in terms of MACs and SNR contrast are shown in Tables I and III. Hence, the proposed ENSRLMS, ENSLMS, ENSSLMS- based adaptive filters are more suitable for health monitoring ECG sensors.

IJSER © 2014

http://www.ijser.org

International Journal Of Scientific & Engineering Research, Volume 5, Issue 3, March-2014

ISSN 2229-5518

1382

ACKNOWLEDGMENT

The authors would like to thank the anonymous reviewers whose careful reviews and detailed comments helped to improve the readability of this paper.

REFERENCES

[1] Y. Der Lin and Y. Hen Hu, “Power-line interference detection and sup-pression in ECG signal processing,” IEEE Trans. Biomed. Eng., vol. 55, pp. 354–357, Jan. 2008.

[2] N. V. Thakor and Y. S. Zhu, “Applications of adaptive filtering to ECG analysis: Noise cancellation and arrhythmia detection,” IEEE Trans. Biomed. Eng., vol. 38, no. 8, pp. 785–794, Aug. 1991.

[3] A. K. Ziarani and A. Konrad, “A nonlinear adaptive method of

elimina-tion of power line interference in ECG signals,” IEEE Trans. Biomed. Eng., vol. 49, no. 6, pp. 540–547, Jun. 2002.

[4] J. M. Leski and N. Henzel, “ECG baseline wander and power line in-terference reduction using nonlinear filter bank,” Signal Process., vol. 85, pp. 781–793, 2005.

[5] C. Meyer, J. F. Gavela, and M. Harris, “Combining algorithms in

auto-matic detection of QRS complexes in ECG signals,” IEEE Trans. Inf. Tech. Biomed., vol. 10, no. 3, pp. 468–475, Jul. 2006.

[6] C. Brouse, G. A. Bumont, F. J. Herrmann, and J. M. Ansermino, “A wavelet approach to detecting electrocautery noise in the ECG,” IEEE Eng. Med. Biol. Mag., vol. 25, no. 4, pp. 76–82, Aug.

2006.

[7] N. V. Thakor, C. Vaz, R. W. Mc Pherson, and D. F. Hanley, “Adaptive Fourier series modeling of time-varying evoked potentials: Study of human somatosensory evoked response to etomidate anesthetic,” Elec-troencephal. Clin. Neurophysiol., vol. 80, no. 2, pp. 108–118, Mar. 1991.

[8] T. Pawar, S. Chaudhuri, and S. P. Duttagupta, “Body movement

activity recognition for ambulatory cardiac monitoring,” IEEE Trans. Biomed. Eng., vol. 54, no. 5, pp. 874–882, May 2007.

[9] S. Graja and J. M. Boucher, “Hidden Markov tree model applied to ECG delineation,” IEEE Trans. Instrum. Meas., vol. 54, no. 6, pp.

2163–2168, Dec. 2008.

[10] S. Mitra, M. Mitra, and B. B. Chaudhuri, “A rough-set-based inference engine for ECG classification,” IEEE Trans. Instrum. Meas., vol. 55, no. 6, pp. 2198–2206, Dec. 2006.

[11] L. Biel, O. Pettersson, L. Philipson, and P. Wide, “ECG Analysis: A new approach in human identification,” IEEE Trans. Instrum. Meas., vol. 50, no. 3, pp. 808–812, Jun. 2001.

[12] E. Kaniusas, H. Pfützner, L. Mehnen, J. Kosel, J. C. Téllez-Blanco,

G. Varoneckas, A. Alonderis, T. Meydan, M. Vázquez, M. Rohn, A. M. Merlo, and B. Marquardt, “Method for continuous nondisturbing monitoring of blood pressure by magnetoelastic skin curvature sensor and ECG,” IEEE Sensors J., vol. 6, no. 3, pp.

819–828, Jun. 2006.

[13] P. Laguna, R. Jané, S. Olmos, N. V. Thakor, H. Rix, and P.

Caminal, “Adaptive estimation of QRS complex by the Hermite model for classi-fication and ectopic beat detection,” Med. Biol. Eng. Comput., vol. 34, no. 1, pp. 58–68, Jan. 1996.

[14] S. Olmos and P. Laguna, “Steady-state MSE convergence analysis in LMS adaptive filters with deterministic reference inputs for biomedical signals,” IEEE Trans. Signal Process., vol. 48, no. 8, pp.

2229–2241, Aug. 2000.

[15] M. Kotas, “Application of projection pursuit based robust

principal component analysis to ECG enhancement,” Biomed. Signal Process. Control, vol. 1, pp. 289–298, Feb. 2007.

[16] E. Floris, A. Schlaefer, S. Dieterich, and A. Schweikard, “A Fast Lane Approach to LMS prediction of respiratory motion signals,” Biomed. Signal Process. Control, vol. 3, pp. 291–299, Jul. 2008.

[17] G. Mihov and I. Dotsinsky, “Power-line interference elimination from ECG in case of non-multiplicity between the sampling rate and the power-line frequency,” Biomed. Signal Process. Control, vol. 3, pp. 334–340, Jun. 2008.

[18] O. Sayadi and M. B. Shamsollahi, “Model-based fiducial points ex-traction for baseline wander electrocardiograms,” IEEE Trans. Biomed. Eng., vol. 55, no. 1, pp. 347–351, Jan. 2008.

[19] R. Sameni, M. B. Shamsollahi, C. Jutten, and G. D. Clifford, “A non-linear Bayesian filtering framework for ECG denoising,” IEEE Trans. Biomed. Eng., vol. 54, no. 12, pp. 2172–2185, Dec. 2007.

[20] C.-A. Lai, “NLMS algorithm with decreasing step size for adaptive IIR filters,” Signal Process., vol. 82, pp. 1305–1316, 2002.

[21] N. Li, Y. Zhang, H. Yanling, and J. A. Chambers, “A new variable step-size NLMS algorithm designed for applications with exponential decay impulse responses,” Signal Process., vol. 88, pp.

2346–2349, Mar. 2008.

[22] M. H. Costa and J. C. M. Bermudez, “A noise resilient variable step-size LMS algorithm,” Signal Process., vol. 88, pp. 733–748,

2008.

[23] S. Zhao, Z. Manb, S. Khoo, and R. W. Hong, “Variable step-size

LMS al-gorithm with a quotient form,” Signal Process., vol. 89, pp.

67–76, 2009.

[24] M. Z. U. Rahman, S. R. Ahamed, and D. V. R. K. Reddy, “Efficient sign based normalized adaptive filtering techniques for cancellation of artifacts in ECG signals : Application to wireless biotelemetry,” Signal Process., vol. 91, pp. 225–239, 2011.

[25] F. Sufi, F. Qiang, I. Khalil, and S. S. Mahmoud, “Novel methods

of faster cardiovascular diagnosis in wireless telecardiology,”

IEEE J. Sel. Areas Commun., vol. 27, no. 4, pp. 537–552, May 2009. [26] S. Koike, “Analysis of adaptive filters using normalized signed re-gressor LMS algorithm,” IEEE Trans. Signal Process., vol. 47, no.

10, pp. 2710–2723, Oct. 1999.

[27] E. Eweda, “Analysis and design of a signed regressor LMS algorithm for stationary and nonstationary adaptive filtering with correlated Gaussian data,” IEEE Trans. Circuits Syst., vol. 37, no. 11, pp. 1367–1374, Nov. 1990.

[28] B. Farhang-Boroujeny, Adaptive Filters-Theory and Applications.

Chichester, U.K.: Wiley, 1998.

[29] S. C. Douglas and T. H.-Y. Meng, “Normalized data nonlinearities for LMS adaptation,” IEEE Trans. Signal Process., vol. 42, no. 6, pp. 1352–1365, Jun. 1994.

[30] S. C. Douglas, “A family of normalized LMS algorithms,” IEEE

Signal Process. Lett., vol. 1, pp. 1352–1365, Mar. 1994.

[31] A. H. Sayed, Adaptive Filters. Hoboken, NJ: Wiley, 2008.

[32] A. N. Ali, Advanced Bio Signal Processing. Berlin, Germany: Springer Verlag, 2009.

IJSER © 2014 http://www.ijser.org