International Journal of Scientific & Engineering Research, Volume 4, Issue 5, May‐2013
ISSN 2229‐5518
P(P ) -nucleus Interactions at 200 GeV/c via
Neural Network Technique
*Mahmoud Y. El-Bakry
Tabuk University, Faculty of Science, Department of Physics, Tabuk, KSA.
**A. Radi, ***El-Sayed A. El-Dahshan
Ain Shams University, Faculty of Science, Department of Physics, Abbassia, Cairo, Egypt.
**The British University in Egypt (BUE).
***Egyptian E-Learning University- 33 El-mesah St., El-Dokki- Giza- Postal code 12611.
M. Tantawy
*Ain Shams University, Faculty of Education, Department of Physics, Roxi, Cairo, Egypt.
*Moaaz A. Moussa
Buraydah Colleges, Al-Qassim, Buraydah, King Abdulazziz Road, East Qassim University, P.O.Box 31717, KSA.
moaaz2030@Yahoo.com
Abstract— P ( P ) -nucleus interactions at 200 GeV/c have been studied. Two cases are considered; the charged pions multiplicity distribution and the negative ones. The neural net work (NN) technique has been adopted to study the same two cases, the trained NN shows a better fitting with experimental data than the PTFM calculations do. The NN simulation results are satisfactory and prove a vital and strong presence in modeling P ( P ) –nucleus interactions at 200 GeV/c. From paper to paper; we prove that the NN technique is better than the old conventional ones.
Index Terms— Artificial intelligence (AI), machine learning (ML), NN technique, multiplicity distribution, (h-A) interactions.
—————————— ——————————
Xperimental data on hadron-nucleus (h-A) interactions at high energies are required for understanding high energy
particular input leads to a specific target output. The objective of this paper is to extract the multiplicity distribution of
interactions. They provide a useful link between hadron-
charged pions for
h A collisions at 200 GeV/c using NNM
hadron (h-h) interactions and the complex phenomena of nuc- leus-nucleus (A-A) interactions. These types of interactions in-
compared to PTFM. Section 2 presents parton two fireball
model PTFM at high energies for the multiparticle production
vestigate space time picture and highlight on phenomenon
in hadron-nucleus
h A
collisions. The NN model is de-
which doesn't exist in (h-h) such as cascade, multi-collisions, gray particles, etc. There are various models for (h-A) interac- tion like collective tube model [1], diffractive excitation mod- el[2], energy flux cascade model [3], quark model [4], intera- nuclear cascade model [5] multiple scattering model [6], hy- drodynamical model [7], and many others .
From view point of parton two fireball model (PTFM), nucleons are treated as composite objects of loosely bound states of the spatially separated constituents (quarks) which in turn are composed of point-like particles (partons) [8]. This may allow one to consider the nucleons as consisting of a fixed num- ber of partons. This nucleon structure has been used in differ- ent models [8-10] along with other assumptions to describe h-A interactions. PTFM, which is proposed by Hagedorn [11] and
scribed in Sections 3, 4. The results and discussion of both
models are compared in Section 5.
Multiplicity of the created charged particles and other parame- ters in h-A interactions can be determined only by the overlap- ping volume participating in the interaction at a given impact parameter [12, 14, 17, 18].
Let us assume that a proton with mass m and radius r0 is in- cident on a nucleus of radius R .The overlapping volume at any impact parameter, V (b), is given by,
developed by Tantawy [12], has been used to explain the high
V (b)
(r
![]()
R 2 r
![]()
2 1 r
(b
![]()
R) 1 r
b R 2
(1)
energy interactions of hadrons and nuclei [12-18]. All these
studies showed qualitative predictions of the measured parame-
0 3 0 3 0
3 0 (
)
ters [19-23].
Analogous to the theoretical approach based on different
If we define a dimensionless impact parameter x =
b
![]()
,
(r0 R)
views, development in the artificial intelligence (AI) field has
given the neural networks a strong presence in high-energy
physics [24-27]. Neural networks are composed of simple in-
terconnected computational elements operating in parallel.
These artificial neural networks (ANNs) are trained, so that a
then the fraction of partons from the projectile that participate in the interaction at a given impact parameter, Z(x), can be giv- en by,
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 5, May‐2013 2
ISSN 2229‐5518
Z(x)
( 1 3 A 1/3 - 1 A) 3 (A 2/3
A - A 1/3 - 1) x
![]()
![]()
![]()
![]()
2 4 4 4
![]()
![]()
![]()
![]()
- 3 (A 1/3 A 2A 2/3 )x 2 3 ( 1 1 A A 2/3 A 1/3 )x 3
(2)
The number of created pions from each fireball ( n
) will be
4 4 3 3
given by,
Z ( x)T
Z ( x)Q
and the statistical impact parameter distribution is given by![]()
n (Z) 0 =
o 2
(7)
P(x)
dx 2 x dx
(3)
Where, Q is the free energy which is carried by the two fire- balls, is the energy required for the creation of one pion.
The total probability of peripheral collisions PPr . will be given
by,
1
From Eqs. (6, 7), the probability of the emission of any num- ber of pions ( n0 ) from one fireball in the peripheral collision
can be obtained in the form:
P Pr.
(x)
2 x dx
a
(4)
n 0 1
k 9
2 n
![]()
1
( A 3 1 )
P ( n o ) dn 0
![]()
2 C k
n k 0
Where, a=![]()
1
( A 3 1 )
k 8
2 n
![]()
k
k 1
2
![]()
0
(8)
The total probability of central collisions will be given by
kC 0 dn
k 0 Q Q
![]()
1
( A 3 r ) 2
It is clear that at a given impact parameter, Eq. (7) gives the
P 0
(5)![]()
Cent .
1
( A 3
r0 )
total number of created particles (i.e. charged and neutral par-
ticles).
From equations (2) and (3) using least square fitting tech- nique Z function distribution can be written in the form [14, 17],
According to the above scheme, the charged multiplicity distribution will be given by,
P(z)
dz 2
k 9
k 0
C Z k
k 8
kC
k 0
Z k 1 dZ
(6)
P (n ch
nch
)
n1
(n)(nch
n) (9)
Where, C k values are represented in table (1),
TABLE 1
;n ch 2,4,6,........Q,
/
C k VALUES FOR CONSIDERED INTERACTIONS
Where,
(n)
=
n 0
( n 2 ) P
( n o )

, (n2)
is the Poisson distribution of the form,
n
N 2
![]()
( ) =
2
p n 2
e - NP
(10)
n 2 !
Where, N: is the number of pairs of created particles from one
fireball ( N ![]()
n 0 ),
2
n 2 the number of pairs of charged
pions, n 2
charged.
n 1
![]()
2
, P the probability that the pair of pions is
The number of negative particles from one fireball equals the
n ch
![]()
half of new created charged pions n
2
The probability distribution of negative particles
P(n ) is
-
the same as the probability distribution of charged particles
IJSER © 2013
P -) P (nch
- )
(11)
International Journal of Scientific & Engineering Research, Volume 4, Issue 5, May‐2013 3
ISSN 2229‐5518
W ( J T J
I ) 1 J T e
; n
0 ,1, 2 ,3,........,
Q / 2
Where, J is the Jacobean matrix of derivatives of each error
with respect to each weight.
J T is the transposed matrix
of J ; I is the identity matrix that has the same dimensions of
ANNs are composed of interconnecting artificial neurons
J T J
, is a scalar; changed adaptively by the algorithm and
(programming constructs that mimic the properties of biologi-
cal neurons). Artificial neural networks may either be used to
gain an understanding of biological neural networks, or for
solving artificial intelligence problems without necessarily
creating a model of a real biological system. The real, biologi-
cal nervous system is highly complex: artificial neural network
algorithms attempt to abstract this complexity and focus on
what may hypothetically matter most from an information
processing point of view.
The neuron transfer function, f, is typically sigmoid or step
function that produces a scalar output (n) as in Eq. (12):
e is an error vector.
The only requirement for this method is a considerably
large memory for large problems. The initial training weights
were also chosen using the Nguyen–Widrow random genera-
tor in order to speed up the training process [27-31].
n f
i w i I i b
(12)
“Figure 1. Neuron model”
th th
Where, I i , w i , b are the i input, the i weight and b the bias respectively.
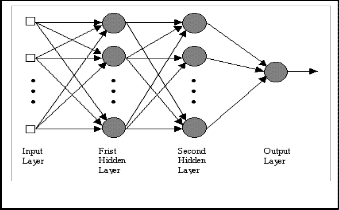
A network consists of one or more layers of neurons. A layer of neurons is a number of parallel neurons. These layers are configured in a highly interconnected topology as shown in figure (1).
Neural network can be trained to perform a particular function by adjusting the values of the connections (weights) between elements. Training in simple is to make a particular input leads to a specific target output. The weights are ad- justed, based on a comparison of the output and the target, until the network output matches the target. Typically many such input/target pairs are used, in this supervised learning, to train a network.
The proposed ANNs in this paper was trained using Le-
venberg–Marquardt optimization technique. This optimiza-
tion technique is more powerful than the conventional gra-
dient descent techniques [27-31].
The Levenberg–Marquardt updates the network weights
using the following rule,
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 5, May‐2013 4
ISSN 2229‐5518
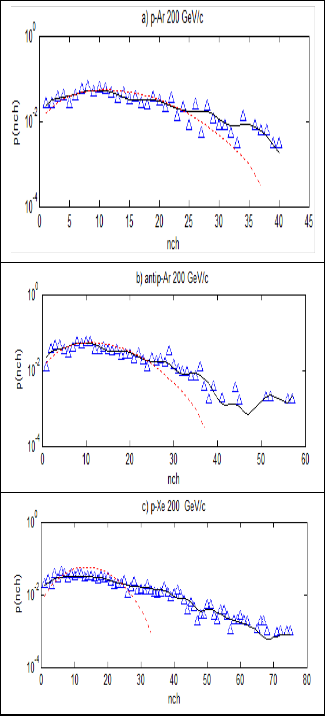
“Figure 2. Comparison between the experimental and simulated multiplicity distribution of charged pions P ( n ch ) for h A collisions at 200 GeV/c:(—) NN model, (……) PTFM, ( ) experimental data”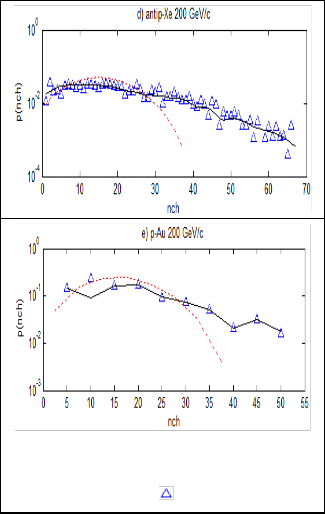
Charged and negative pions multiplicity distributions, Eq.
ment. The input and target vectors are randomly divided into three sets (validation set, training set, testing set), 80% of the vectors are used to train the network and 20% of the vectors are used to validate how well the network generalized.
(9, 11), are calculated for p Ar40 , p Xe131 ,
and p He 4 assuming in Eq. (11) is given by :
an b
p Au 197
Where, a = 0.04, b= 0.35 as in references [14, 17, 18]. The results
of these calculations are represented in figure 2 (a, b, c, d, e)
and figure 3 (a, b, c, d, e, f) along with experimental data [32,
34] which show fair agreement with the corresponding expe- rimental data. It can be seen from figs. (2, 3) that charged and negative pions multiplicity distributions are not in accordance with the experimental data for heavy nuclei although the situ- ation becomes better for the light ones. The emission of sec-
The proposed neural network model of charged and nega-
ondary particles is assumed to follow a Poisson distribution.
tive pions multiplicity distributions of
p Ar40 , p Xe131
As mass number increases the multiplicity distribution is not
, p Au 197 and
p He 4 collisions at 200 GeV/c have three
broaden but its peak is shifted to high numbers.
We have also calculated the same collisions by using ANN model and these calculations are represented in figs (2, 3) along with the same experimental data [32-34]. We have also found great variations compared to PTFM.
Different configurations of network structure were investi-
gated to achieve good mean squared error (MSE) and good
performance for the network using the input-output arrange-
inputs ( nch , PLab , A ), one output P(nch ) and two hidden lay- ers of 23, 22 neurons, for charged pions, two hidden layers of
24, 21 neurons for negative ones. The transfer functions of the first and second hidden layers were chosen to be a tan sigmo- id, while the output layer was chosen to be a pure line. The trained method which used to train the ANN model is Leven- berg-Marquardt optimization technique, with number of
epochs=19, performance of order 105 for charged pion pro-
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 5, May‐2013 5
ISSN 2229‐5518
duction and epochs=10, performance of order 104
tive ones.
for nega-
is why; we use the ANN technique because it is able to exactly model the multiplicity distribution for different beams in ha- dron nucleus interactions.
Our obtained function for charged and negative pions in h-A intteractions is generated using the obtained control NN para- meters as follows:
The structure of the network is 3-23 -22-1 for charged pions and
3-24 -21-1 for negative ones. The obtained equation which de- scribes the multiplicity dustribution of charged and negative pions in h-A intteractions for different beams (projectiles), dif- ferent mass numbers (nucleii) at the same energy is given by: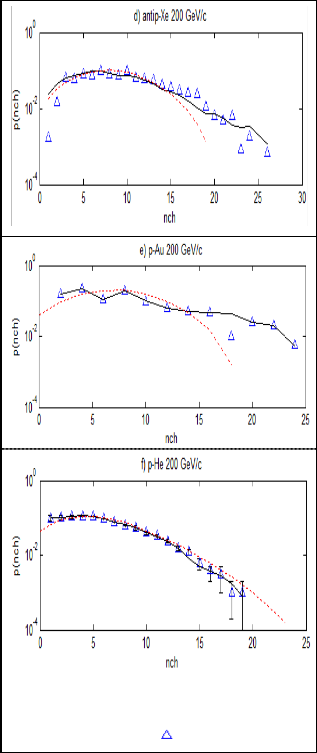
P(nch )
pureline[{net.LW (3,2). tan sigmoid .{net.
LW (2,1). tan sigmoid {net .IW (1,1).P net .b(1)}
net.b(2)} net.b(3)}]
Where, pure line is linear transfer function, tan sigmoid is hyperbolic tangent sigmoid transfer function.
P is the input which is ( nch , PLab , A ).
net .LW (3, 2 ) linked weight between the second hidden layer
and the output.
net .LW
( 2 ,1) linked weights between the first and the second
hidden layer.
net .IW (1,1) linked weights between the input layer and the first hidden layer.
net .b (1) is the bias of the first hidden layer.
net .b ( 2 ) is the bias of the second hidden layer.
net .b (3) is the bias of the output layer.
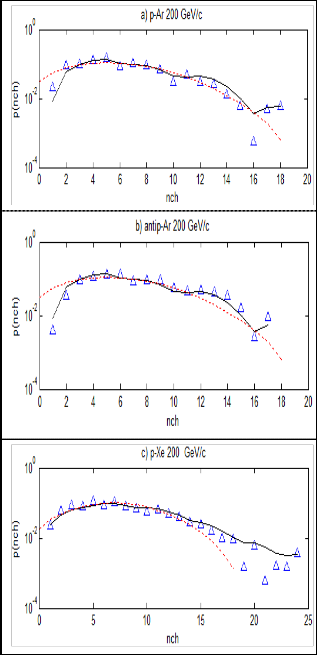
“Figure 3. Comparison between the experimental and simulated multiplicity distribution of
[1] S. Fredriksson, Preprint Ref. TH. 2720-CERN, August (1979). [2] A. Dar and J. Vary Phys Rev D 6, 2412 (1972).
[3] K. Gottfried Phys. Rev. Lett 32, 957 (1974).
[4] Yoichiro Nambbu, The Conference of Quarks Scientific American
(1976).
[5] V. S. Barashenkov et al., Sov. Phys. Usp 16, 31 (1973); Yu. P. Nikitin et al, Sov. Phys. Usp 20, 1 (1977).
[6] A. Capella and A. Krzywicki, Phys. Rev. D 18, 3357 (1978).
[7] D. Amati et al., Nuovo Cimento. 26, 896 (1962); F. Zachariasen, Phys.
Rep., C 2, 1 (1971).
[8] R. P. Feynman, photon-Hadron Interactions (Benjamin, Reading, Mas- sachusetts, 1972).
[9] E. Fermi, Prog. Theor. Phys. 5 , 570 (1950).
pions P ( n )
for h A collisions at 200 GeV/c: (—)
[10] J. Ranft, Phys. Lett, B 31, 529 (1970).
NN model, (……) PTFM, ( ) experimental data”
It is should be emphasized that when the mass increases the multiplicity distributions of charged and negative pion production using ANN are consistent with all regions of the experimental data (low, medium, high multiplicity). In con- trary with PTFM, the theoretical calculations are inconsistent with the experimental data especialy at high multiplicity. That
[11] R. Hagedorn, Nuovo Cimento Suppl. 3, 147 (1965); R. Hagedorn and J.
Ranft, Nuovo Cimento Suppl.6, 169 (1968).
[12] M. Tantawy Ph. D. Dissertation, Rajasthan University (Jaipur-India) (1980).
[13] D.M.Habashy, Ph. D. Dissertation, Ain Shams University (Cairo-Egypt)
(2011).
[14] Ehab G. Abbas, M. Sc. Thesis Ain Shams University (Cairo-Egypt) (2010)
[15] Moaaz A. Moussa, M. Sc. Thesis Ain Shams University (Cairo-Egypt)
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 5, May‐2013 6
ISSN 2229‐5518
(2009)
[16] S. Gamiel, M. Sc. Thesis Ain Shams University (Cairo-Egypt) (1997)
[17] M. El-Mashad, Ph. D. Dissertation, Cairo University (Cairo-Egypt) (1994).
[18] M.Y. El-Bakry, M. Sc. Thesis, Ain Shams University (Cairo-Egypt) (1987).
[19] T. I. Haweel, M. Y. El-Bakry, K. A. El-Metwally, Chaos, Solitons and
Fractals 18, 159 (2003).
[20] M. Y. El-Bakry, Chaos, Solitons and Fractals 18, 995(2003).
[21] M. Tantawy, M. El-Mashad, S. Gamiel and M. S. El-Nagdy Chaos, Solitons and Fractals 13, 919 (2002).
[22] M. Tantawy, M. El-Mashad, M. Y. El-Bakry. Indian J Phys.72A, 110
(1998).
[23] M. Tantawy, M. El Mashad, M. Y. Elbakry, The 3rd International Con- ference on Engineering Mathematics and Physics (ICEMP) Faculty of Eng., Cairo university, 23rd–25th Dec. (1997).
[24] AK Hamid, Can. J. Phys. 7, 76 (1998)
[25] P. Bhat, Using neural networks to identify jets in hadron–hadron colli- sions. Proceedings of The 1990 Summer Study on HEP, (1990), Re- search Directions––the Decade, Snowmass, Colorado
[26] RP. Lippman, IEEE Acoust Speech Signal Process Mag. (1987)
[27] M.T. Hagan, Menhaj M.B, IEEE Trans Neural Networks 6:861–7 (1994) [28] El-Sayed El-dahshan, A. Radi. Cent. Eur. J. Phys. 9(3), 874-883 (2011)
[29] S. Y. El-Bakry, El-Sayed El-dahshan, M. Y. El-Bakry. Ind. J. Phys., 85 (9),
1405-1413 (2011)
[30] S. Y. El-Bakry, El-Sayed El-dahshan, S. Al-Awfi and M. Y. El-Bakry.
ILNouvo Cimento, 125B (10), (2010)
[31] El-Sayed El-dahshan, A. Radi and M. Y. El-Bakry. Int. J. Mod. Phys. C,
20(11), 1817-825 (2009)
[32] C. De Marzo et al, Phys Rev,D 26,1019 (1982). [33] D. H. Brick et al., Phys. Rev. D 39, 2484 (1989).
[34] W. Bell et al., Phys. Lett. B128, 349 (1983).
IJSER © 2013