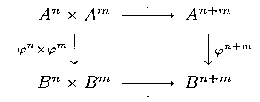International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 767

ISSN 2229-5518

Multilinear Algebras and Tensors with Vector

Bundles of Manifolds

Md. Abdul Halim1 Md. Shafiqul Islam2 Sajal Saha3

Abstract− In this paper some important aspects of tensor algebra, tensor product, exterior algebra, symmetric algebra, module of section, graded algebra, vector subbundles are studied. The purpose of this paper is to develop the theories which are based on multi-linear algebra and tensors with vector bundles of manifolds. A

Theorem 1.34. is established by using sections and fibrewise orthogonal sections of an application of Gran-Schmidt.

Keywords: Multilinear and tensor algebra, tangent and tensor bundle, subbundles, associated frame bundles, graded and Symmetric algebra.

——————————  ——————————

I. INTRODUCTION

ultilinear algebra and tensor algebra of 𝑅 − modules are
needed to use higher order tensors. The tangent bundle,
various tensor bundles, subbundles and associated frame
bundles will play important roles as the theory of manifolds is developed. A theorem related with subbundle is treated with various tensors, graded algebras, tensor product, and trivial bundles.

II. TENSOR ALGEBRA

We build a universal model of multi-linear objects called the tensor
algebra over 𝑅 in order to study 𝑅 −multilinear maps, , where
𝑅 will be the ring 𝐶 ∞(𝑀).

Definition 1.1 [1] An 𝑅 −module 𝑉 is free if there is a subset 𝐵 ⊂

𝑉 such that every nonzero element 𝑣 ∈ 𝑉 can be written uniquely as
a finite 𝑅 −linear combination of elements of 𝐵. The set 𝐵 will be
called a (free) basis of 𝑅.

Example 1.2 Let 𝜋 ∶ 𝐸 → 𝑀 be a trivial 𝑛 − plane bundle. Then

Γ(𝐸) is a free 𝐶 ∞ (𝑀) −module on a basis of n elements.
Example 1.3 The integer lattice ℤ𝑘 , a free ℤ −module is a
𝐶 ∞ (𝑀) module.
Definition 1.4 If 𝑉1 , 𝑉2 , 𝑉3 are objects in ℳ(𝑅), a map 𝜑 ∶ 𝑉1 ×
Definition 1.5 [2] A tensor product of 𝑅 −modules 𝑉1, 𝑉2 is an
𝑅 −module 𝑉1 ⨂ 𝑉2, together with an 𝑅 −bilinear map
⨂ ∶ 𝑉1 × 𝑉2 → 𝑉1 ⨂ 𝑉2
with the following “universal property”:given any 𝑅 −modules 𝑉3
and any 𝑅 −bilinear map
𝜑 ∶ 𝑉1 × 𝑉2 → 𝑉3 ,
there is a unique 𝑅 −linear map 𝜑� ∶ 𝑉1 ⨂ 𝑉2 → 𝑉3 such that the
diagram

⨂
𝑉1 × 𝑉2 𝑉1 ⨂ 𝑉2
𝜑 𝜑�
𝑉3
commutes. Write ⨂ (𝑣, 𝑤) = 𝑣 ⨂ 𝑤.
Corollary 1.6 If 𝑉𝑖 is an 𝑅 −module, 𝑖 = 1, 2, 3, there are unique
𝑅 −linear isomorphism
𝑉2 → 𝑉3 is 𝑅 − 𝑙𝑖𝑛𝑒𝑎𝑟 if
𝑉 ⨂ (𝑉
⨂ 𝑉 ) = (𝑉 ⨂ 𝑉 ) ⨂ 𝑉
= 𝑉 ⨂ 𝑉 ⨂ 𝑉

1 2 3

1 2 3 1 2 3

𝜑(. , 𝑉2 ) ∶ 𝑉1 → 𝑉3
𝜑(𝑉1, . ) ∶ 𝑉2 → 𝑉3

are 𝑅 − linear, ∀ 𝑣𝑖 ∈ 𝑉𝑖 , 𝑖 = 1,2.

————————————————

1. IUBAT- International University of Business Agriculture and Technology, Dhaka-1230, Bangladesh,, PH: 880- 1710226151, e-mail- halimdu226@gmail.com

2. IUBAT- International University of Business Agriculture and Technology, Dhaka-1230, Bangladesh,, PH: 880- 1913004750, e-mail- shafiq_mju@yahoo.com

3. IUBAT- International University of Business Agriculture and Technology, Dhaka-1230, Bangladesh,, PH: 880- 1724493092, e-mail- sajal.saha@iubat.edu

identifying
𝑣1 ⨂ (𝑣2 ⨂ 𝑣3 ) = (𝑣1 ⨂ 𝑣2) ⨂ 𝑣3
= 𝑣1 ⨂ 𝑣2 ⨂ 𝑣3, ∀ 𝑣𝑖 ∈ 𝑉𝑖 , 𝑖 = 1,2,3.
Definition 1.7 An element 𝑣 ∈ 𝑉1 ⨂ … ⨂ 𝑉𝑘 is said to be

decomposable if it can be written as a monomial 𝑣 =

𝑣1⨂ … ⨂ 𝑣𝑘 , for suitable elements 𝑣𝑖 ∈ 𝑉𝑖 , 1 ≤ 𝑖 ≤ 𝑘. Otherwise, 𝑣
is said to be indecomposable.

Lemma 1.8 If 𝑉 and 𝑊 are 𝑅 −modules with respective bases 𝐴 and

𝐵, then 𝑉 ⨂ 𝑊 is free with basis 𝐶 = {𝑎 ⨂ 𝑏 | 𝑎 ∈ 𝐴, 𝑏 ∈ 𝐵}.

Proof. An arbitrary element 𝑣 ∈ 𝐴 ⨂ 𝐵 can be written as a linear

combination of decom-posable. A decomposable element 𝑉 ⨂ 𝑊
can be expanded the multilinearity of tensor product, to a linear

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 768

ISSN 2229-5518

combination of elements of C, proving that 𝐶 spans 𝑉 ⨂ 𝑊. It
remains to show that, if

Proposition 1.13 There is a unique 𝑅 −linear map

𝑝,𝑞

𝑙 ∶ 𝑉∗ ⨂ … … … ⨂𝑉∗ → (𝑉 ⨂ … … . ⨂ 𝑉 )∗
� 𝑐𝑖𝑗 𝑎𝑖 ⨂ 𝑏𝑗 = � 𝑑𝑖𝑗 𝑎𝑖 ⨂ 𝑏𝑗 ,

1 𝑘 1 𝑘

𝑖,𝑗=1

which on decomposable elements has the formula
where 𝑎𝑖 ∈ 𝐴 and 𝑏𝑗 ∈ 𝐵, 1 ≤ 𝑖 ≤ 𝑝, 1 ≤ 𝑗 ≤ 𝑞 then all 𝑐𝑖,𝑗 =
𝑑𝑖,𝑗 . Subtracting one expression from the other, we only need to
prove that

𝑝,𝑞

� 𝑐𝑖𝑗 𝑎𝑖 ⨂ 𝑏𝑗 = 0

𝑖,𝑗=1

𝑙(𝜂1⨂ … … . ⨂ 𝜂𝑘 ) (𝑣1 ⨂ … … . ⨂ 𝑣𝑘 ) = 𝜂1 (𝑣1)⨂ … … . ⨂ 𝜂𝑘 (𝑣𝑘 ).
If the 𝑅 −modules 𝑉𝑖 are all free on finite bases, then 𝑙 is a
canonical isomorphism.

Proof. Since the decomposable span, uniqueness is immediate. For existence, consider the multi linear functional

∗ × … … … × 𝑉∗ × 𝑉 × … … .× 𝑉

→ 𝑅
implies that all 𝑐𝑖 ,𝑗 = 0. The bilinear functional 𝜑 ∶ 𝑉 × 𝑊 →
𝑅 corresponds one to one to any functions 𝑓 ∶ 𝐴 × 𝐵 → 𝑅.The
correspondence is 𝜑 ↔ 𝜑 | (𝐴 × 𝐵). Thus, the linear functional
𝜃 ∶ 𝑉1
by

𝑘 1 𝑘

𝜑� ∶ 𝑉 ⨂ 𝑊 → 𝑅 also corresponds one to one to these functions
𝑓 ∶ 𝐴 × 𝐵 → 𝑅.
If (𝑎, 𝑏) ∈ (𝐴 × 𝐵), let 𝑓𝑎,𝑏 ∶ (𝐴 × 𝐵) → 𝑅 be the function
taking the value 1on (a,b) and the value 0 on every other element
of (𝐴 × 𝐵).The corresponding linear functional will be denoted by

𝜑� 𝑎,𝑏 . Applying 𝜑� 𝑎𝑖 ,𝑏𝑗 to equation (1.1), we see that all 𝑐𝑖𝑗 = 0.

This completes the proof.
Proposition 1.9 If 𝜆𝑖 ∶ 𝑉𝑖 → 𝑊𝑖 is an 𝑅 −linear map, 1 ≤ 𝑖 ≤ 𝑘,
there is a unique 𝑅 −linear map
𝜆1 ⨂ … … . ⨂ 𝜆𝑘 ∶ 𝑉1 ⨂ … … . ⨂ 𝑉𝑘 → 𝑊1 ⨂ … … . ⨂ 𝑊𝑘
which, on decomposable elements, has the formula
𝜃(𝜂1 , … … . , 𝜂𝑘 , 𝑣1 … … , 𝑣𝑘 ) = 𝜂1 (𝑣1) … … . 𝜂𝑘 (𝑣𝑘 ).
by the universal property, this gives the associated linear functional
𝜃� : 𝑉1 ⨂ … … … ⨂ 𝑉𝑘 ⨂ 𝑉1 ⨂ … … . ⨂ 𝑉𝑘 → 𝑅,

∗ ∗

and we define
𝑙 ∶ 𝑉∗ ⨂ … … … ⨂𝑉∗ → (𝑉 ⨂ … … . ⨂ 𝑉 )∗

1 𝑘 1 𝑘

by
𝑙(𝜂)(𝑣) = 𝜃� (𝜂 × 𝑣).
If �𝑣𝑖,1 , … … , 𝑣𝑖,𝑚 � is a basis of 𝑉𝑖 , 1 ≤ 𝑖 ≤ 𝑘, let �𝑣 ∗ , … … , 𝑣 ∗ � be

𝑖 𝑖,1 𝑖,𝑚𝑖

the dual basis. Let 𝐵 and 𝐵∗ be the respective bases of

∗ ∗

(𝜆1⨂ … … . ⨂ 𝜆𝑘 ) (𝑣1⨂ … … . ⨂ 𝑣𝑘 ) = 𝜆1 (𝑣1)⨂ … … . ⨂ 𝜆𝑘 (𝑣𝑘 ).
𝑉1 ⨂ … … . ⨂ 𝑉𝑘 and 𝑉1 ⨂ … … … ⨂ 𝑉𝑘 given by the Corollary 1.11.
The formula

Proof. We know the decomposable span. So, the uniqueness is

𝑙(𝑣1,𝑗

𝑘,𝑗𝑘

1,𝑖

𝑘,𝑖 𝑖

𝑖 𝑖 …..….𝑖

∗ ⨂ … … ⨂ 𝑣∗ )(𝑣

⨂ … … ⨂𝑣

) = 𝛿 𝑗1 … … 𝛿 𝑗𝑘 = 𝛿 𝑗1 ……𝑗𝑘

immediate. For existence, let us define the multilinear map 1

1 𝑘 1

𝑘 1 𝑘

𝜆 ∶ 𝑉1 × … … .× 𝑉𝑘 → 𝑊1⨂ … … . ⨂ 𝑊𝑘
by
𝜆(𝑣1, … … . , 𝑣𝑘 ) = 𝜆1 (𝑣1)⨂ … … . ⨂ 𝜆𝑘 (𝑣𝑘 ).
Then 𝜆1 ⨂ … … . ⨂ 𝜆𝑘 is defined to be the unique associated linear
map. Hence, the proof is complete.

Definition 1.10 For the module of 𝑅 −linear functionals, the

𝑑𝑢𝑎𝑙 𝑉∗ of an 𝑅 −module 𝑉 is 𝐻𝑜𝑚𝑅 (𝑉, 𝑅).
shows that 𝑙 carries the basis 𝐵∗ one to one onto the basis dual to 𝐵, so 𝑙 is an isomorphism. This completes the proof.
Definition 1.14 [3] A graded (associated) algebra 𝐴 over 𝑅 is a sequence {𝐴𝑛 }∞ of 𝑅 −modules, together with 𝑅 −bilinear maps
(multiplication)
𝐴𝑛 × 𝐴𝑚 → 𝐴𝑛+𝑚 , ∀ 𝑛, 𝑚 ≥ 0,
which is strongly associative in the sense that the compositions

.×𝑖𝑑 .

(𝐴𝑛 × 𝐴𝑚 ) × 𝐴𝑟 �⎯� 𝐴𝑛+𝑚 × 𝐴𝑟 → 𝐴𝑛+𝑚+𝑟
Lemma 1.11 If 𝑉 has a finite free basis {𝑣1, … … … , 𝑣𝑛 }, then 𝑉∗

𝑛 𝑚

𝑟 𝑖𝑑 ×. 𝑛

𝑚+𝑟 .

𝑛+𝑚+𝑟

has a finite free basis {𝑣1 , … … … , 𝑣𝑛 }, called the basis and defined
by
𝐴 × (𝐴
× 𝐴 ) �⎯� 𝐴
× 𝐴
→ 𝐴
𝑣 ∗ �𝑣 � = 𝛿 𝑖 , 1 ≤ 𝑖, 𝑗 ≤ 𝑛.

𝑖 𝑗 𝑗

are equal, ∀ 𝑛, 𝑚, 𝑟 ≥ 0.
Definition 1.14 The graded algebra 𝐴 is connected if 𝐴0 = 𝑅 and
Corollary 1.12 If 𝑉1, … … . , 𝑉𝑘 are free 𝑅 −modules on bases

0 𝑚 ∙

𝑚 ∙ 𝑚 0

𝐵1 , … … . , 𝐵𝑘 , respectively, then 𝑉1 ⨂ … … . ⨂ 𝑉𝑘 is a free
𝐴 × 𝐴
→ 𝐴
← 𝐴
× 𝐴
𝑅 −module with basis
𝐵 = {𝑣1 ⨂ … … . ⨂ 𝑣𝑘 | 𝑣𝑖 ∈ 𝐵𝑖 , 1 ≤ 𝑖 ≤ 𝑘}.
are equal to scalar multiplication, ∀ 𝑚 ≥ 0.

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 769

ISSN 2229-5518

Definition 1.15 If 𝑉 is an 𝑅 −module, then 𝒯(𝑉) with multiplication ⨂, is called the tensor algebra of 𝑉. It is clear that the tensor algebra 𝒯(𝑉) is connected.

Definition 1.16 A homomorphism 𝜑 ∶ 𝐴 → 𝐵 of graded 𝑅- algebras
is a collection of 𝑅- linear maps 𝜑𝑛 ∶ 𝐴𝑛 → 𝐵𝑛 , ∀ 𝑛 ≥ 0 , such that

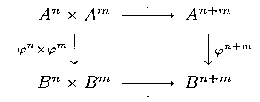
the diagrams
commute, ∀ 𝑛, 𝑚 ≥ 0. The homomorphism 𝜑 is an isomorphism
if 𝜑𝑛 is bijective, ∀ 𝑛 ≥ 0.

Theorem 1.17 If 𝜆 ∶ 𝑉 → 𝑊 is an 𝑅 −linear map, then there is a

unique induced homomorphism 𝒯(𝜆): 𝒯(𝑉) → 𝒯(𝑊) of graded
𝑅 −algebras such that 𝒯 0(𝜆) = 𝑖𝑑𝑅 and 𝒯1 (𝜆) = 𝜆. This homo-
orphism satisfies
𝒯 𝑛 (𝜆)(𝑣1 ⨂ 𝑣2 ⨂ … … . ⨂ 𝑣𝑛) = 𝜆 (𝑣1) ⨂ 𝜆 (𝑣2 ) ⨂ … … . ⨂ 𝜆(𝑣𝑛),
∀ 𝑛 ≥ 2, ∀ 𝑣𝑖 ∈ 𝑉, 1 ≤ 𝑖 ≤ 𝑛.
Finally, this induced homomorphism makes 𝒯 a covariant function
from the category of 𝑅 −modules 𝑅 −linear maps to the category
of graded algebras over 𝑅 and graded algebra homomorphisms.

Definition 1.18 The space of tensors on 𝑉 of type (𝑟, 𝑠) is the

tensor product

Proof. Let 𝑉 be an 𝑅 −module where 𝑣 ∈ 𝑉. Then

𝑣 = 0 ⇒ 𝑣 = −𝑣.
For the converse
𝑣 = −𝑣 ⇒ 2𝑣 = 0
⇒ 𝑣 = 1/2(2𝑣)
⇒ 𝑣 = 1/2(0)
∴ 𝑣 = 0.
This completes the proof.

Definition 1.21 Let 𝑉 and 𝑊 be 𝑅- modules. An antisymmetric

𝐾 − 𝑙𝑖𝑛𝑒𝑎𝑟 𝑚𝑎𝑝 𝜑 ∶ 𝑉𝑘 → 𝑊 is a 𝐾 − linear map such that
𝜑�𝑣𝜎(1) , … … … , 𝑣𝜎(𝑘) � = (−1)𝜎 𝜑 (𝑣1, 𝑣2, … … , 𝑣𝑘 ),
∀ 𝑣1, 𝑣2, … … , 𝑣𝑘 ∈ 𝑉, ∀ 𝜎 ∈ ∑ 𝑘
where (−1)𝜎 = � 1, σ an even permutation,
−1, σ an odd permutation.
Lemma 1.22 If 𝜑 ∶ 𝑉𝑘 → 𝑊 is antisymmetric, then 𝜑� �𝔄𝑘 (𝑉)� =
{0}.

Proof. It will be enough to show that 𝜑� vanishes on a set spanning

𝔄𝑘 (𝑉). Thus, if𝑤 ∈ 𝒯 𝑝 (𝑉) 𝑢 ∈ 𝒯 𝑞 (𝑉), 𝑝 + 𝑞 = 𝑘 − 2, and 𝑣1, 𝑣2 ∈
𝑉, we will show that
𝜑� (𝑤 ⨂ (𝑣1⨂ 𝑣2 + 𝑣2⨂ 𝑣1) ⨂ 𝑢) = 0.
But the antisymmetry of 𝜑 implies that

𝑟 𝑟 0

𝒯𝑠 (𝑉) = 𝒯0 (𝑉) ⨂ 𝒯𝑠 (𝑉).
A tensor 𝛼 𝜖 𝒯 𝑟 (𝑉) is said to have covariant degree 𝑟 and
contravariant degree 𝑠.

III. EXTERIOR ALGEBRA

Let 𝑅 be any commutative ring with unity 1 such that 1 𝜖 𝑅. That

is, if 2 = 1 + 1 𝜖 𝑅, then 1 𝜖 𝑅 has the property that 1 ∙ 2 = 1. In
𝜑� (𝑤 ⨂ 𝑣1 ⨂ 𝑣2⨂ 𝑢) = −𝜑� (𝑤 ⨂ 𝑣2⨂ 𝑣1 ⨂ 𝑢),
and the assertion follows the linearity.
Definition 1.23 An element 𝑤 ∈ Λ𝑘 (𝑉) that can be expressed in the form 𝑣1 ∧ 𝑣2 ∧ … … ∧ 𝑣𝑘 , where 𝑣𝑖 ∈ 𝑉, 1 ≤ 𝑖 ≤ 𝑘, is said to be decomposable. Otherwise, 𝑤 is indecomposable.

Definition 1.24 A graded algebra 𝐴 is anticommutative if 𝛼 ∈ 𝐴𝑘

2 2

the case that 𝑅 = 𝔽 is a field, this means that the characteristic of 𝔽
is not 2.

Definition 1.19[4] The exterior algebra of 𝑉 is the connected

graded R-algebra
Λ(V) = {Λ𝑘 (𝑉)}k=0
with multiplication

Λ𝑝 (𝑉) × Λ𝑞 (𝑉) → Λ𝑝+𝑞 (𝑉)
where, the 𝑅 −module Λ𝑘 (𝑉) is the k th exterior power of 𝑉.

Lemma 1.120 Let 𝑉 be an 𝑅 −module, 𝑣 ∈ 𝑉. Then 𝑣 = −𝑣 ⟺

𝑣 = 0.
and 𝛽 ∈ 𝐴𝑟 ⇒ 𝛼𝛽 = (−1)𝑘𝑟 𝛽𝛼.

Corollary 1.25 [5] The graded algebra Λ(V) is anticommutative.

Proof. It is enough to verify the Definition 1.20 for decomposable

elements of Λ𝑘 (𝑉)and Λ𝑟 (𝑉). But that case is an elementary consequence of the case 𝑘 = 𝑟 = 1, and this latter case is given by
𝑣 ∧ 𝑤 = 𝑣 ⨂ 𝑤 + 𝔄2 (𝑉)
= 𝑤 ⨂ 𝑣 + 𝔄2 (𝑉)
= −𝑤 ∧ 𝑣,
∀ 𝑣, 𝑤 ∈ 𝑉. Thus the graded algebra Λ(V) is anticommutative.

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 770

ISSN 2229-5518

Corollary 1.26 If 𝑤 ∈ Λ2𝑟+1 (𝑉), then 𝑤 ∧ 𝑤 = 0.
𝑤1 ∧ 𝑤2 ∧ … … ∧ 𝑤𝑘 = ∑𝑘
𝑎𝑖 𝑤𝑖 ∧ 𝑤2 ∧ … … ∧ 𝑤𝑘 = 0.
Proof. Let 𝑤 ∈ Λ2𝑟+1 (𝑉). Then
𝑤 ∧ 𝑤 = (−1)(2𝑟+1)(2𝑟+1) (𝑤 ∧ 𝑤)
= 𝑤 ∧ 𝑤
Now, by using Lemma 1.17., we have
𝑤 ∧ 𝑤 = 0.
This completes the proof
Conversely, if the set is linearly independent, extend it to a basis by
suitable choices of 𝑤𝑘+1 , … … , 𝑤𝑚 ∈ 𝑉. Then, we have
𝑤1 ∧ 𝑤2 ∧ … … ∧ 𝑤𝑘 ∧ … … ∧ 𝑤𝑚
is a basis of the one-dimensional space Λ𝑚 (𝑉), hence is not 0.
This completes the proof.

Lemma 1.29 If 𝑉 is a free 𝑅 −module on a finite basis, then each 𝐴𝑘

is one to one, hence 𝐴 ∶ Λ(V) ↪ 𝒯(𝑉) is a canonical graded linear
imbedding.
Lemma 1.27 If 𝜆 ∶ 𝑉 → 𝑉 is linear, then Λ𝑚 (𝜆 ) ∶ Λ𝑚 (𝑉) →

Proof. Let {𝑒 , … … , 𝑒

} ⊂ 𝑉 be a basis and consider the basis
Λ𝑚 (𝑉) is multiplication by det(𝜆).
Proof. Relative to a basis {𝑒1 , … … , 𝑒𝑚 } of 𝑉, write

1 𝑚

�𝑒𝑖1 ∧ … … ∧ 𝑒𝑖𝑘 �

1≤𝑖1 ≤⋯…<𝑖𝑘≤𝑖𝑚

∗ ∗ ∗

𝑘 ∗

𝑚 of Λ𝑘 (𝑉). Let {𝑒1 , … … , 𝑒𝑘 } ⊂ 𝑉

be the dual basis. Since 𝒯 (𝑉 ) =
𝜆(𝑒 ) = � 𝑎𝑗 𝑒 , 1 ≤ 𝑖 ≤ 𝑚
𝒯𝑘
(𝑉)∗ , we obtain a subset

𝑗=1

∗ ⨂ … … ⨂ 𝑒∗ �

⊂ 𝒯𝑘 (𝑉)∗ ,
then,
�𝑒𝑗1

𝑗𝑘 1≤𝑗 <⋯…<𝑗 ≤𝑗

1 𝑘 𝑚

Λ𝑚 (𝜆 )(𝑒1 ∧ … … ∧ 𝑒𝑚 ) = 𝜆 (𝑒1) ∧ … … ∧ 𝜆 (𝑒𝑚 )
which is a part of a free basis. Then, since 𝑗1 < ⋯ < 𝑗𝑘 and
𝑖1 < ⋯ < 𝑖𝑘 ,

𝑚 𝑗

= �∑𝑗=1 𝑎1 𝑒𝑗 � ∧ … … ∧ �∑𝑗=1 𝑎𝑚 𝑒𝑗 �

∗ ∗ 𝑘

𝑗1

1≤𝑗1 ,……,𝑗𝑚≤𝑚 1

… … 𝑎𝑗𝑚
𝑒𝑗1 ∧ … … ∧ 𝑒𝑗𝑚 .
(𝑒𝑗1 ⨂ … … ⨂ 𝑒𝑗𝑘 )(𝐴 (𝑒𝑖1 ∧ … … ∧ 𝑒𝑖𝑘 ))

∗ ∗ 𝜎

Any term with a repeated j index vanishes. If 𝐽 =
= (𝑒𝑗1 ⨂ … … ⨂ 𝑒𝑗𝑘 ) �∑𝜎∈∑ 𝑘(−1) 𝑒𝑖𝜎(1) ⨂ … … ⨂ 𝑒𝑖𝜎(𝑘) �

∗ ∗

(𝑗1 , 𝑗2 , … … , 𝑗𝑚 ) contains no repetitions, there is a unique permutation 𝜎 𝑗 ∈ ∑ 𝑚 such that
𝑗𝜎𝑗 (𝑟) = 𝑟, 1 ≤ 𝑟 ≤ 𝑚.
Thus,
Λ𝑚 (𝜆 )(𝑒1 ∧ … … ∧ 𝑒𝑚 )
= (𝑒𝑗1 ⨂ … … ⨂ 𝑒𝑗𝑘 )(𝑒𝑖1 ⨂ … … ⨂ 𝑒𝑖𝑘 )

𝑗1…𝑗𝑘

𝑖1 …𝑖𝑘

and the assertion follows.

IV. SYMMETRIC ALGEBRA

= �∑𝜎∈∑ 𝑚(−1)𝜎 𝑎1
… … 𝑎𝑚 � 𝑒 ∧ … … ∧ 𝑒
A 𝐾 −linear map 𝜑 ∶ 𝑉𝑘
→ 𝑊 is symmetric if, for each 𝜎 ∈ ∑ 𝑘,
= det(𝜆)(𝑒1 ∧ … … ∧ 𝑒𝑚 ).
Hence, the proof is complete.
𝜑 �𝑣𝜎(1) , … … , 𝑣𝜎(𝑘) � = 𝜑(𝑣1 , 𝑣2 , … … , 𝑣𝑘 ), ∀ 𝑣1 , 𝑣2 , … … , 𝑣𝑘 ∈ 𝑉.
In the usual way, we build a universal, symmetric, 𝐾 −linear map
Lemma 1.28 If 𝑅 is a field, a set of vectors 𝑤1, 𝑤2, … … , 𝑤𝑘 ∈
𝑉, 𝑘 ≥ 2, is linearly independent if and only if 𝑤1 ∧ 𝑤2 ∧ … … ∧
𝑉𝑘
→ 𝔄𝑘 (𝑉),
𝑤𝑘 ≠ 0.

Proof. If 𝑅 is a field then consider the set of

vectors 𝑤1, 𝑤2, … … , 𝑤𝑘 ∈ 𝑉, 𝑘 ≥ 2. Again if the set is dependent,
the existence of universe in 𝑅 allows us to assume, without loss of
generality, that

𝑘

𝑤1 = � 𝑎𝑖 𝑤𝑖 .

𝑖 =2

Then
usually written with the dots
(𝑣1, 𝑣2, … … , 𝑣𝑘 ) ⟼ 𝑣1 𝑣2 … … 𝑣𝑘 .
Definition 1.30 [6] The space 𝔄𝑘 (𝑉) is called the k th symmetric
power of 𝑉, where, as usual, 𝔄0 (𝑉) = 𝑅 and 𝔄1(𝑉) = 𝑉. The
connected, graded algebra 𝔄(𝑉) = {𝔄𝑘 (𝑉)}∞ , with multiplication
". ", is called the symmetric algebra of 𝑉.

Definition 1.31 Let 𝑉 be a finite dimensional vector space over a field

𝔽. A function 𝑓 ∶ 𝑉 → 𝔽 is a homogeneous polynomial of degree 𝑘
on 𝑉 if, related to some basis {𝑒1 , … … , 𝑒𝑚 } of 𝑉,

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 771

ISSN 2229-5518

𝑚

𝑓 �� 𝑥𝑖 𝑒𝑖 � = 𝑃(𝑥1 , … … , 𝑥𝑚 )

𝑖 =1

is a homogeneous polynomial of degree 𝑘 in the variables
𝑥1 , … … , 𝑥𝑚 . The vector space of all homogeneous polynomials of
degree 𝑘 on 𝑉 will be denoted by 𝑃𝑘 (𝑉).

V. THE MODULE OF SECTIONS

We are going to view the set of all vector bundles over a fixed
manifold 𝑀[5] as the objects of a category 𝑉𝑀 . Let
𝜋 ∶ 𝐸 → 𝑀
𝜌 ∶ 𝐹 → 𝑀
be vector bundles differing fibers dimensions. A homomorphism
of the 𝑛 −plane bundle 𝐸 to the 𝑚 −plane bundle 𝐹 is denoted by HOM (𝐸, 𝐹) is naturally called 𝐶 ∞ (𝑀) − module.
Theorem 1.32[7] The 𝐶 ∞ (𝑀) −linear map 𝛼 is a canonical isomorphism of 𝐶∞(𝑀) − modules.

𝛤(𝐸) ⨂𝐶 ∞(𝑀) 𝛤(𝐹) = 𝛤(𝐸 ⨂ 𝐹).

Corollary 1.30[7] There are canonical iso- morphisms 𝐶 ∞(𝑀) −
of point wise tensor products of sections trivializes the bundle
𝐸 ⨂ 𝐹, hence this is also a free basis of 𝛤(𝐸 ⨂ 𝐹). Since

𝛼 �𝜎𝑖 ⨂𝐶 ∞(𝑀) 𝒯𝑗 � = 𝜎𝑖 ⨂ 𝒯𝑗 ,

for all relevant indices, we see that 𝛼 is an isomorphism of
𝐶 ∞ (𝑀) − modules. This completes the proof.

Theorem 1.34 If 𝐹 ⊆ 𝐸 is a vector subbundle and if there is given

Riemannian metric on 𝐸, then the subset 𝐹� ⊆ 𝐸, fiber wise
perpendicular to 𝐹, is a subbundle.

Proof. Here the local triviality all that needs to be proven. There are

sections 𝜎1 , … … , 𝜎𝑟 , 𝜎𝑟 +1 , … … , 𝜎𝑛 of 𝐸|𝑈, trivializing that bundle, where 𝑈 is a neighborhood of an arbitrary point of 𝑀. These can be chosen so that 𝜎1 , … … , 𝜎𝑟 are sections of 𝐹|𝑈 which trivialize that
bundle an application of Gran-Schmidt turns these into fiberwise
orthonormal sections 𝑆1 , … … , 𝑆𝑟 , 𝑆𝑟 +1 , … … , 𝑆𝑛 with the same properties. It follows that 𝑆𝑟+1 , … … , 𝑆𝑛 are trivializing sections of
𝐹� |𝑈, proving that 𝐹� is a subbundle of 𝐸. Hence the proof is
complete.

VI. CONCLUSION

A theorem 1.34 is established which is related with a Riemannian
metric on the bundle 𝑀 × 𝑉. For each 𝑥 ∈ 𝑀, let 𝐸�
modules
𝛤�𝒯𝑘 (𝐸)� = 𝒯𝑘 (𝛤(𝐸))
𝛤�𝛬𝑘 (𝐸)� = 𝛬𝑘 (𝛤(𝐸))
𝛤�𝑆𝑘 (𝐸)� = 𝑆𝑘 �𝛤(𝐸)�.

Proof. The first part of these identities is an immediate consequence

of theorem 1.29. There is canonical inclusion
𝐴𝑘 ∶ 𝛬𝑘 (𝛤(𝐸)) ↪ 𝒯𝑘 (𝛤(𝐸))
𝐴𝑘 ∶ 𝛤�𝛬𝑘 (𝐸)� ↪ 𝛤�𝒯𝑘 (𝐸)�.
The second part comes from the bundle inclusions. The images of
these inclusions correspond perfectly under the identification
𝒯𝑘 �𝛤(𝐸)� = 𝛤�𝒯𝑘 (𝐸)�, proving the second identity. Similarly the
third part can be proof which is same as proof of second part.
Lemma 1.33 If F and 𝐸 are trivial bundles, then 𝛼 is an isomorphism of 𝐶 ∞ (𝑀) − modules.
Proof. In this case we choose the global sections {𝜎1 , … … , 𝜎𝑛 } of 𝐸 and {𝒯1 , … … , 𝒯𝑚 } of 𝐹 which trivialize these bundles. These are free bases of the respective 𝐶 ∞ (𝑀) − modules 𝛤(𝐸) and 𝛤(𝐹),
so

𝑥 ⊂ {𝑥} × 𝑉 be

the subspace orthogonal to 𝐸𝑥 . Consequently the set 𝐸� = ⋃𝑥∈𝑀 𝐸�𝑥
is a subbundle of 𝑀 × 𝑉. Also this theorem will follow form a
theorem in dimension theory.

REFERENCES

1. Boothby, W. 1975. An Introduction to Differentiable Manifolds and Differential Geometry, Academic Press, NewYork..
2. Donson, C.T.J. and Poston, T. 1997.Tensor Geometry, Pitman,
London
3. Ahmed, K. M., 2007. A study of Graded manifolds, Dhaka Uni. J. Sci. 55 (1): 35-39
4. Chevally, C. 1956. Fundamental Concepts of Algebra, Academic

Press, New York.

5. Brickell, F. and Clark, R.S.1970.Differential Manifolds, Van

Nostrand Reinhold company, London

6. Myers, S.B. and N.E. 1939.Steenrod, the group of isometrics of a
Riemannian Manifold, Ann of Math. 40: 400-416.
7. Auslander, L. and R.E. Mackenzie, 1963. Introduction to differential Manifolds, Mc Graw-Hill, New York

𝑛,𝑚

�𝜎𝑖 ⨂𝐶 ∞(𝑀) 𝒯𝑗 �

is a free basis of 𝛤(𝐸) ⨂𝐶 ∞(𝑀) 𝛤(𝐹). The set

𝑛,𝑚

�𝜎 ⨂ 𝒯�

𝑖,𝑗=1