Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 2 , Fe bruary -2012 1

ISSN 2229-5518

Manipulation of Near-wall Structure in a Boundary Layer Subjected to Concentrated Suction and Roughness Strip

O.M. Oyewola

Abs tract— Hot-w ire measurements have been made in a turbulent boundary layer subjected to a short roughness strip and concentrated suction w ith the view to examine their combined eff ect on the near -w all boundary layer structure. The suction is applied through a porous w all strip f or a range of suction rate. The results indicate that, the combination of suction and roughness strip alter s the pseudo-equilibrium of the boundary layer through the modif ication of the length scale of the turbulence structure in a phenomenological manner, suggesting that there is a possibility of them acting independently on the diff erent mechanism of the boun dary layer. While the application of suction w eakened the structure, it is reactivated in the presence of the roughness element.

Inde x Terms— Boundary layer, Length scale, Measurement, Near -w all, Structure, Suction, Turbulence

——————————  ——————————

1 INTRODUCTION

A major feature of wall turbulence is its self-sustainability. This indicates that energy is generated by the interaction between the boundary layer and the wall to compensate for the viscous losses. This however implies that the wall itself provides a continuous source of shear or mean vorticity through the no-slip condition. The study of how turbulent shear flows respond to various perturbations has been a subject of interest in the last few years [1]. The continuous progress has led to significant improvement in flow control, especially our basic understanding of the interaction between the flow and wall region of the boundary layer has improved to some certain degree. For instance, [2] experimentally considered the response of a turbulent boundary layer to a short roughness strip using Laser Doppler Velocimetry (LDV). They found that, relative to the undisturbed smooth wall, the roughness strip increased the turbulent stresses in the region between the two internal layers originating at the upstream and downstream edges of the strip. They also showed that near-wall anisotropy was decreased downstream of the roughness strip. Suta rdi and Ching [3] used hot-wire anemometry to examine the effect of different sized transverse square grooves on a turbulent boundary layer. They concluded that the effects of the grooves are more significant at the higher Reynolds number with the most pronounced effects caused by the largest size groove. More over considerable works has been done on the turbulent boundary layer subjected to localise wall suction [4], [5].
Oyewola et al. [5] examined the effect concentrated wall
suction can have on the anisotropy of the Reynolds stress tensor. Their results indicated that the large-scale motion of the boundary layer was significantly altered by suction and the global anisotropy of the layer increases with the suction rate. In order to gain insight into the dynamics of the layer, the present study examines the manipulation of the boundary layer with the combination of concentrated suction and roughness strip using cross correlation functions. This is necessary in order to understand the behaviour of the near- wall structure and its length scale to such a perturbation.
Nomenclature:
b Width (m)
D Diameter for pipe (m)
h Channel half width (m)
k Wave number
L Length (m)
p Pressure (kg/m sec2)
q Energy (kgm2/sec2)
Q Flow rate (m3/sec) U Velocity (m/sec)
V Suction velocity (m/sec)
x Streamwise location (m)
y Distance normal to the wall (m)
Greek Letters:
Boundary layer thickness (m) Shear stress (kg/m sec2) Momentum thickness (m) Severity index
Kinematic viscosity (Ns/m2) Subscripts:
c Centre
β u or v or w
r Radius (m)
u Streamwise velocity
v Wall normal velocity
w Spanwise velocity w Wall
* Normalisation with Kolmogorov variables

http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 2 , Fe bruary -2012 2

ISSN 2229-5518

2 MEASUR EMENT DETAILS AND COND ITIONS

Experiments were made in a smooth flat plate turbulent boundary layer, which is subjected to the combination of short roughness strip and concentrated suction, applied through a short porous strip. The turbulent boundary layer develops on the floor of the wind tunnel working section (Fig. 1) after it is tripped at the exit from a two-dimensional 9.5:1 contraction using a 100 mm roughness strip (Norton Bear No. 40, very coarse). Tests showed that the boundary layer was fully d e- veloped at the suction strip location, which is about 1200 mm downstream of the roughness strip. The roof of the working section is adjusted to achieve the desire pressure gradient (ze- ro for the present investigation). The free stream velocity U1 was approximately 7 m/sec. A 3.25 mm thick porous strip with a width of 40 mm and made of sintered bronze with pore sizes in the range 40-80 m or (0.4-0.9)/U was mounted flush with the test section floor. Allowing for the width of the mounting recess step, the effective width (=b) of the strip was
35 mm. Suction was applied through a plenum chamber l o- cated underneath the suction strip and connected to a suction blower, driven by a controllable DC motor, through a circular pipe (internal diameter D = 130 mm and L/D  38, where, L, is the pipe length). The flow rate Qr was estimated directly by radially traversing a Pitot tube located near the end of the pipe, for various values of the pipe centre-line velocity (Uc). A plot of Qr vs Uc, allowed the suction velocity (Vw) to be in- ferred via the continuity equation (Qr = AwVw, where, Aw is the cross-sectional area of the porous strip). The suction veloc- ity was assumed to be uniform over the porous surface; this assumption seems reasonable if the variation in the permeabi l- ity coefficient of the porous material is 3%.

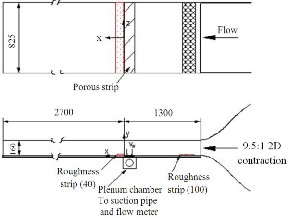
Fig.1: Schematic arrangement of the experimental set up

———— ——— ——— ——— ———

 Oyewola Miracle Olanrewaju is currently Associate Professor in the Department of Mechanical Engineering in University of Ibadan, Nig eria masters degree program in electric power engineering in University. E- mail: ooyewola@yahoo.com

The short roughness strip made up of uniform sandpaper (40 grade) of 40 mm long in the streamwise direction and 1 mm above the smooth wall is placed just immediately after the suction strip. The initial momentum thickness Reynolds num- ber Ro (Ro = U1o/, where, o is the momentum thickness at the leading edge of the suction strip when no suction is a p- plied) is 1400. The suction rate  ( = Vwb/oU1, where, Vw and b are the suction velocity and width of the porous strip respectively) is in the range  = 0-5.5. Measurements of the velocity fluctuations in the streamwise and wall normal direc- tions were made with hot cross wires, each inclined at nomi- nally 45° to the flow direction. The etched portion of each wire (Wollaston, Pt-10% Rh) had a diameter of 2.5 µm and a length to diameter ratio of about 200. The separation between the inclined wires was about 0.6 mm. The velocity fluctuation in the spanwise direction was also measured by rotating the same X-probe through 90°. All hot wires were operated with in-house constant temperature anemometers at an overheat ratio of 1.5. The uncertainties in the streamwise, wall normal and spanwise velocity components were 3, 5 and 4%, respec- tively.

3 RESULTS

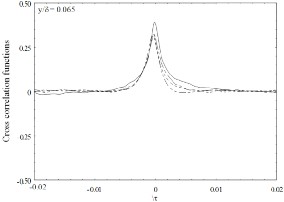
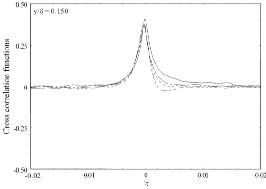
The results of cross correlation functions of u and v when suction alone is applied are shown in Fig. 2 for y/  = 0.050,
0.065 and 0.150. These are necessary in order to provide a

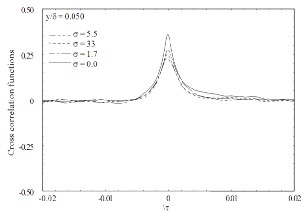
better frame work for the effect of the combination of suction and roughness strip on the turbulence structure to be quantified. As a reference, the results when no suction is applied are also included. From the Fig. 2a, all values of cross correlation functions are reduced when suction is applied throughout the time delay, the reduction increasing as the suction rate increases. The reduction observed in the cross correlation functions when suction is applied may suggests a change in the near wall quasi-streamwise vortices.

(a)

http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 2 , Fe bruary -2012 3

ISSN 2229-5518

(b)

(c)
Fig. 2: Distributions of cross correlation functions for several
 at (a) y/ = 0.050; (b) y/ = 0.065; (c) y/ = 0.150
This is not surprising since near-wall quasi-streamwise vortices are thought to play an important role in the near-wall dynamics of the flow especially in the context of momentum transfer, the reduction in the cross correlation functions reveals that the vortical structures has been diminished as a result of significant reduction in the streamwise length scale in this region of the boundary layer. Reference to no suction, the peak value decreases by 25, 35 and 45 for  = 1.7, 3.3 and
5.5 respectively. These changes may be as a result of the
stabilisation of the near-wall flow.

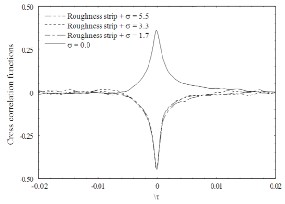
(a)

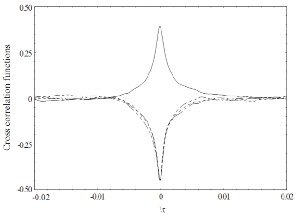
(b)

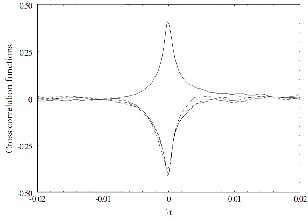
(c)
Fig. 3: Distributions of cross correlation functions for several
 at (a) y/  = 0.050; (b) y/ = 0.065; (c) y/ = 0.150
This corroborates the flow visualisation of [6]. Djenidi et al. [6] found that the low-speed str eaks downstream of th e suction strip are much longer and less agitated in the spanwise direction when suction is applied.
Meanwhile as y / increases, the effect of suction is reduced.
For instance, at y / = 0.150, the distributions almost recover to no suction value especially for negative time delay.
Figure 3 shows the combination of suction and roughness strip for y / = 0.050, 0.065 and 0.150. In contrast to smooth wall, the distributions displace more of negative cross correlation functions throughout the regions of the boundary layer observed. This is likely to be associated with the large scale streamwise vortical motions, which occur one after the other with opposite signs of rotation. There is a considerable change in the distributions with reference to the smooth wall . If the distributions of the combination of suction and roughness strip are transpose, the results shows that, for τ (time delay)
<0, the combination of suction and roughness strip rises above the smooth wall, overshoot for τ = 0 and lies below the smooth wall for τ>0 in all the regions considered. This would indicate that the near-wall vortical structures downstream of the combination of suction and roughness strip have been altered.

http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 2 , Fe bruary -2012 4

ISSN 2229-5518

This alteration would give rise to a modification in the streamwise length scale of the structure. The overshoot may suggest that the flow is more intermittent over the roughness strip than on the smooth wall. This intermittency would definitely influences the length scale of the structure. It should be noted that [2] showed that the near-wall anisotropy was decreased downstream of the roughness strip and [5] found that anisotropy increases downstream of the suction strip. The present result would argumentatively suggest that the modification on the length scale is on the basis of suction and roughness strip acting independently on the different mechanism of the layer and these influences would alter the pseudo-equilibrium of the layer in a phenomenological manner.

4 CONCLUSIONS

The manipulation of turbulence in a boundary layer subjected to an impulse in form of short roughness strip and concentrated wall suction has been investigated through the analysis of cross correlation functions. The results indicate that, the pseudo-equilibrium of the layer has been altered in a phenomenological manner by suction and roughness strip. The manner whereby the alterations occurred suggests that the individual effect on the mechanism of the layer is preserved. While suction acts to weaken the near-wall structure, roughness acts to reactivate the structure as indicated by the decreases in the peak of cross correlation functions for suction and increases for the combination of suction and roughness strip. Although, the increases are in the negative direction, it reveals the action of roughness s trip on the dynamics of the layer, which, in turn, influence the flow structure especially near the wall.

REFERENCES

[1] M. Gad-el-Hak, “Flow Control: Fundamental and Practices ," Lecture Note in Physics, M. Gad-el-Hak, A. Pollard and J.P. Bonnet, eds., Springer, pp. 1-154, 1998.

[2] B.R. Pearson, R. Elavasaran and R.A. Antonia , "Effect of a Short

Roughness Strip on a Turbulent Boundary Layer," Applied Science Re- search, vol. 59, pp. 61-75, 1998.

[3] A.S. Sutardi and C.Y. Ching, “Effect of Different Sized Transverse Square Grooves on a Turbulent Boundary Layer,” Experiment In Flu- ids, vol. 34, pp. 261-274, 2003.

[4] O. Oyewola, L. Djenidi and R.A. Antonia, "Combined Influence of

the Reynolds Number and Localised Wall Suction on a Turbulent

Boundary Layer," Experiment In Fluids, vol. 35, pp. 199-206, 2003.

[5] O. Oyewola, L. Djenidi, and R.A. Antonia, “Influence of Localised Wall Suction on the Anisotropy of the Reynolds Stress Tensor in a Turbulent Boundary Layer,” Experiment In Fluids, vol. 37, pp. 187-193,

2004.

[6] L. Djenidi, P.E. Gall, A. Vincent, and R.A. Antonia, “Effect of Wall

Suction on the Structure of a Turbulent Boundary Layer,” Proc.of the

11th International Symp. on Application of Laser Techniques to Fluid Me-

chanics, Lisbon, 2002,

http :// www.ijser.org