International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 1

ISSN 2229-5518

MULTIPLE MOBILE AGENTS IN WIRELESS SENSOR NETWORKS USING GENETIC ALGORITHM

LingaRaj.K, Aradhana.D, Nagaveni.B.Biradar

Abstract— It has been proven recently that using Mobile Agent (MA) in wireless sensor networks (WSNs) can drastically help to obtain the flexibility of application-aware deployment. Normally, in any MA based sensor network, it is an important research issue to find out an optimal itinerary for the MA in order to achieve efficient and effective data collection from multiple sensory data source nodes. In this paper, we firstly investigate a number of conventional single MA itinerary planning based schemes, and then indicate some shortcomings of these schemes, since only one MA is used by them. Having these investigations and analysis, a novel genetic algorithm based multiple MAs itinerary planning (GA-MIP) scheme is proposed to address the shortcomings of large latency and global unbalancing of using single MA, and its effectiveness is proved by conducting the extensive experiments in professional environment.

Index Terms— Minimum Wireless sensor networks, Mobile Agents, Genetic Algorithm, Local Closest First, Mobile Agent Itinerary

Planning, Global Closest First, Single MA Itinerary Planning.

——————————  ——————————

1 INTRODUCTION

A wireless sensor network (WSN) consists of spatially distrib- uted autonomous sensors to cooperatively monitor physical or environmental conditions, such as temperature, sound, vibra- tion, pressure, motion or pollutants. The development of WSNs was motivated by military applications, such as battle- field surveillance. They are now used in many industrial and civilian application areas, including industrial process moni- toring and control, machine health monitoring, environment and habitat monitoring, healthcare applications, home auto- mation, and traffic control.
Mobile Agent (MA) system [2] can cope with situation aware applications e.g., habitat monitoring and medical care, in WSNs. As a special kind of software, MA migrates among network nodes to carry out task(s) autonomously, e.g., collect- ing sensory data from a number of source nodes, and flexibly to handle network dynamics, in order to achieve the specific requirements of the agent dispatcher (i.e., the sink node). MA system has been proven to be an efficient approach to enhance such capabilities of WSNs. Normally, the MA design in WSNs can be decomposed into four components, i.e., 1) architecture,
2) itinerary planning, 3) middleware system design and 4)
agent cooperation. Among these four components, itinerary planning determines the order of sensory data source nodes to be visited during the MA migration, which has a sig- nificant impact on the performance of the MA systems. Thus, find out an optimal itinerary for the MA to visit a number of

————————————————

 LingaRaj.k is currently pursuing master’s degree program in Computer Network Engineering in VTU University, India. E-mail: linga- raj.k@live.com

 Aradhana.D is currently Working has lecture in BITM, Bellary in VTU, University, India. E-mail: aradhanabm@rediffmail.com

 NagaVeni.B.Biradar is currently Working has lecture in RYMEC, Bellary in VTU, University, India. E-mail: Veer_nagaveni@yahoo.com

source nodes is critical. However, finding an optimal itinerary had already been proven to be NP-hard, generally heuristic algorithms are proposed and applied to compute competitive itineraries with sub-optimal performance.
A number of itinerary planning schemes have been proposed
in recent researches [7][8][9][10], but most of them focus only on the single MA problem in WSNs. Although, using MA in WSNs can help to obtain the flexibility of application aware deployment, sometimes, using only single MA in a WSN can also bring some visible shortcomings, e.g., the long latency and the global unbalancing. In order to address these short- comings of using only single MA, multiple MAs itinerary planning is then proposed in. Following the same approach, but different idea, in this paper, a novel genetic algorithm (GA) based multiple MAs itinerary planning (GAMIP) scheme is proposed, which mainly aims at optimizing the number of MAs and planning an efficient itinerary for each MA.
To realize the GA-MIP algorithm, we encode the Source Node
Sequence and the Source Node Group into numbers as the genes for genetic evolution. First, we set up a searching space filled with randomly selected genes. Then, we perform an iter- ative evolution approach. In each iteration, evolution opera- tors such as crossover and mutations are applied to increase the variety of the genes. After these procedures, the selection operator selects the better genes to survive for the next genera- tion, which is analogous to the natural-selection in the real world. After a number of evolution iterations, the solution corresponding to an efficient strategy of itinerary planning will be obtained. A genetic algorithm (GA) is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems. Genetic algorithms be- long to the larger class of evolutionary algorithms (EA), which generate solutions to optimization problems using techniques inspired by natural evolution, such

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 2

ISSN 2229-5518

as inheritance, mutation, selection, and crossover. The scien- tific research contributions of this research work include the following points:
• Novelty: To the best of our knowledge, this research work is
the first effort that tries to solve the MIP problem based on the genetic algorithm.
• Optimization: Different from previous MIP solution [11],
which divides the MIP solution into 3 components:
1) finding the optimal number of MAs 2) grouping source
nodes for MAs 3) determining the visiting sequence for each
MA, the proposed GA-MIP scheme consider finding the opti- mal number of MAs, subsets for source nodes and the visiting sequence for each MA as ONE problem. It provides sub- optimal solution with shorter task duration and lower com- munication cost while the computational complexity is not relevant to the number of source nodes.

2 RELATED WORK

A number of researches have been conducted for MA itinerary planning in WSNs [7] [8] [9] [10] [12] [11]. Among these previous heuristic proposals, Local Closest First (LCF) and Global Closest First (GCF) are the simplest approaches [8] for MA itinerary plan- ning. LCF searches for the next sensory data source node with the shortest distance to the current node while GCF selects the closest node to the sink node as its next source node. MADD [7] is similar with LCF but selects the farthest source node as the starting point of the itinerary. All of these three approaches are not energy effi- cient as indicated in [9], in which the authors propose a better scheme named IEMF1. IEMF extends LCF by considering estimat- ed communication cost, and achieves further reduction on energy consumption by choosing the first source node to be visited accord- ing to the estimated communication cost, since choosing different first source nodes results in different total communication cost. In [10], a genetic algorithm based mobile itinerary planning is pro- posed to exploit the global information of sensor detection signal levels and link power consumption.
However, all of these researches only focus on the single MA itin- erary planning (SIP) problem. Thus, they have some intrinsic shortcomings of using single MA, especially when the number of source nodes is large [12], e.g., 1) Delay Issue: extensive delay is needed when a single agent works for a network consisting of hundreds of or even thousands of sensor nodes; 2) Traffic Load Issue: in the perspective of the whole network, the traffic load is put on the nodes along the single flow. Therefore, sensor nodes trav- ersed in the agent itinerary will deplete their energy much quicker than other nodes. This drawback will reduce the lifetime of the network2.
To address these problems, a multiple mobile agent’s itinerary
planning (MIP) is proposed in [11], in which we discover a dense
centre of source nodes and then organize the sources nodes in a predefined radius R as a group for one MA. This procedure repeats until all source nodes are visited. However, this paper still leaves an open research issue on choosing the optimal number of source nodes, in order to minimize the total communication cost.

3 NETWORK MODEL

The considered WSN in this paper consists a number of dense- ly and randomly deployed static sensor nodes. A static sink node is deployed in the central location of the sensor network, with infinite power supply and strong computational capabil- ity. A number of sensory source nodes are randomly deployed in the WSN. All the sensor nodes have the uniform transmis- sion radius, and any two directly connected (1-hop) sensor nodes have the stable bi-directional communication. The de- gree of the sensor nodes deployment density can guarantee that each sensor node has at least two 1-hop neighbour nodes. A number of MAs can be issued by the sink node to visit the randomly deployed source nodes simultaneously with differ- ent itineraries, in which each MA has its own itinerary for vis- iting a subset of the total source nodes.

Fig. 1. An Example of studied Network Model.

4 GENETIC ALOGRITHM

4.1 Introduction to Genetic Algorithm

Genetic Algorithm (GA) is adaptive heuristic search algorithm based on the evolutionary theory of genetic and natural selection, which will produce the fittest survival. In a GA system, each solu- tion to the problem was described as an individual with genetic information in the nature. The solutions produce children that in- herit mixture characteristics from their parents. Meanwhile, an opportunistic mutation may happen to generate new individuals. Through the evaluation by a fitness function, the better individuals could survive. As time goes on, the survivals contain the excellent genes which represent the better solutions to the problem.

4.2 The GA-MIP Scheme

In this section, we introduce the GA-MIP scheme.

Definition 1. Code of Source node Sequence. The Code of Source

Node Sequence is an array of the source nodes’ identifiers, which
implies the order for a MA to visit the corresponding source nodes.
One MA can have only one final Code of Source Node Sequence
for its visiting itinerary.

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 3

ISSN 2229-5518

Definition 2. Code of Source node Group. The Code of Source Node Group is an array of integer numbers, in which each number indicates the number of source nodes that are allocated in the cor- responding Source Node Group.

4.3 Encoding scheme

To enable GA implementation, we must present a solution to the problem as a gene. In GA-MIP, a gene consists of two parts:
(1) Code of Source Node Sequence (sequence array);(2) Code of Source Node Group (group array). Note that the combination of sequence array and group array represents one itinerary planning solution.
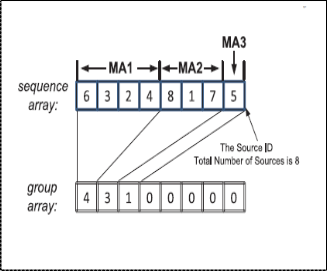
We denote the output of Source Node Sequence encoding by se- quence array, and denote the output of Source Node Group encod- ing by group array. The number of non-zero elements in group array represents the number of MAs. The value of each non-zero element denotes the number of source nodes to be visited by the corresponding MA. The three non-zero elements (i.e., 4,3,1) in the group array correspond to three MAs. The first MA will visit 4 source nodes in the order of 6, 3, 2, 4; MA2 will visit the source nodes in the order of 8, 1, 7; and MA3 will visit the source node with ID of 5 in Fig2.

Theorem1. The proposed encoding mechanism in GAMIP scheme ensures each combination of sequence array and group array can only represent one unique MIP solution.

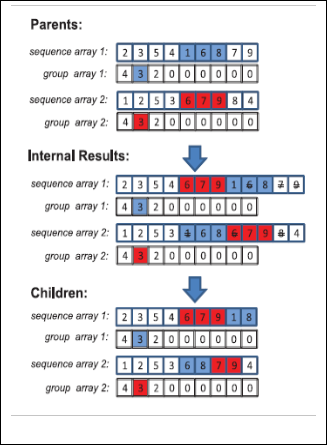
non-zero element (denoted by m) in group array. Corresponding to its associated sequence array, m is mapping to a sequence segment. The two sequence segments which are located in the same posi- tions in the two sequence arrays will be exchanged each other in our crossover procedure.Fig 3 as an example, we assume that ele- ment “3” in group array was selected as the indicator of the crosso- ver section. Thus, the segment “1-6-8” in sequence array 1 is insert- ed into the associated position of sequence array 2, vise versa. This operation produces two arrays with 12 elements, which we call it “Internal Results” in the figure. Apparently, the they are invalid since they include duplicate elements (e.g., nodes 6, 7, 9 in sequence array 1, nodes 1, 6, 8 in sequence array 2. Thus, the elimination pro- cedure is required for producing the final children arrays.

Fig. 2. The Encoding Examples with 3 MAs and 8 Source

Nodes.

4.4 Operator

In this section, we describe the genetic operators for the GA-MIP scheme. As conventional operators for GA, we implemented the crossover, mutation and selection operators.
1) Crossover Operators: Crossover operator is an essential operator in GA. It imitates the way of natural biological evolution. In previ- ous GA works, there are several crossover schemes have been pro- posed, such as one-point crossover and multi-point crossover. However, we have to find out a proper way of crossover to inherit the better genes in the search space for our evaluation criterion.
In our approach, crossover is only applied between the sequence arrays attach with the same group array. We first randomly select a

Fig. 3. The Example of Sequence Crossover.

2) Mutation Operators: The mutation operator is used to keep the variety of the genes so that the discovery of new solutions is possi- ble. In our approach, both sequence array mutation and group ar- ray mutation are implemented.
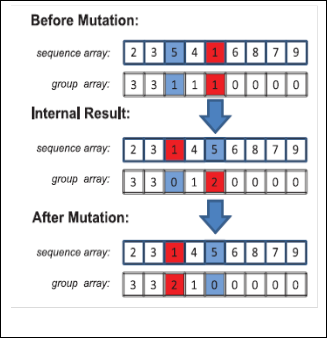
Fig.4. as example. For the sequence array, the operator randomly selects two elements in the array and switches their positions. For the group array, similar operation is performed that a non-zero element with larger value will be decreased by 1 and a smaller el- ement will be increased by 1.
Note that we have to guarantee the elements in group array is in numerical order, thus a sort for the group array should be per- formed after the random mutation. After the decrease in third ele- ment and the increase in fifth element, the group array shown as “Internal Result” in the figure is not in numerical order. It requires a sorting to produce the final group array. Otherwise, the solution

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 4

ISSN 2229-5518

repetition cannot be avoided.

Fig. 4. The Example of Sequence Crossover.

3) Selection Operators: For the purpose of selecting the better genes to survive for the evolution at the next round, we pro- pose a fitness function to evaluate the performance of a gene. As to obtain an efficient solution, we employ the same criteri- on to estimate the communication cost of an itinerary. During the GA evolution, the ith gene corresponds to a planned itin- erary, whose cost is denoted by EI (i), i = 1...k, where k is the size of the search space. After the crossover and mutations, the number of genes is increased to (1+α)k.5 In our implementa- tion, the select operator select first k genes according to the their better EI s.

5 SIMULATION

5.1 Simulation Setup

We implemented the proposed GA-MIP algorithm as well as existing SIP algorithm using .NET Frameworks and C#.The same network model in [11] is adopted, in which the nodes are uniformly deployed within a 1000m×500mfield, and the sink node is located at the centre of the field and multiple source nodes are randomly distributed in the network. To verify the scaling property of our algorithms, we select a large-scale network with 800 nodes.

5.2 Evaluation metric’s

In order to evaluate the time and energy efficiency from the simulation results, we consider the following four perfor- mance metrics, as several previous works [9] [11]:

1. Estimated Cost: The value of estimated energy cost calculated by the fitness function. Even though these values are just approximate energy cost in the net- work, they still could be criteria to evaluate the con- vergence of the GA evolution progress.

2. Task Duration: In a SIP algorithm, it is equivalent to

average end-to-end report delay, which is the average
delay from the time when a MA is dispatched by the sink to the time when the agent returns to the sink an MIP algorithm, since multiple agents work in parallel, there must be one agent which returns to the sink at last. Then, the task duration of an MIP algorithm is the delay of that agent.

3. Average Communication Energy: The total communi-

cation energy consumption, including transmitting,
receiving, retransmissions, overhearing and collision, to obtain each sensory data from all the target sources.

4. Energy-Delay Product (EDP): For time-sensitive ap- plications over energy constrained WSNs, EDP (calcu- lated by EDP = energy × delay) gives us a unified view. The smaller the value of is, the better the uni- fied performance will be.

5.3 Performance comparison of GA-MIP and LCF

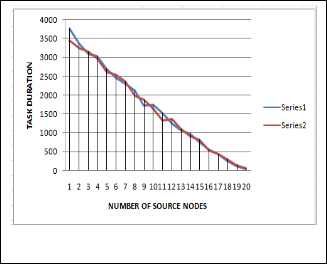
Fig. 5. The impact of number of source nodes on Task Duration
As shown in figure above GA-MIP has larger advantage over. The reason for this phenomenon is that in single MA systems, one MA should travel along the whole network to collect in- formation in all sensor nodes. This procedure will cost a larger latency since the sensor nodes are always distributed all over the network. Multiple MAs can speed up the task because more than two itineraries are applied simultaneously
However, the integrated performance of delay and energy (i.e., EDP) is an important overall criterion in many applica- tions, especially for delay constraint traffic in wireless sensor network, such as wireless multimedia sensor network, and video sensor networks. It shows that GA-MIP algorithm achieves the best overall performance among the three

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 5

ISSN 2229-5518

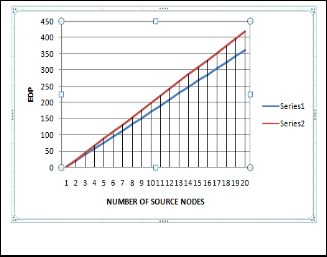
schemes, which verifies effectiveness of the proposed algo- rithm.

Fig. 6. The impact of number of source nodes on Task Duration

6 CONCLUSION

Applying MAs in WSNs can facilitate a large number of loca- tion aware applications. In this paper, we first investigate sev- eral existing SIP solutions to indicate the shortcoming of using MA, such as larger latency and global unbalancing in large scale WSNs. These challenging issues need to be addressed to enable MA based systems being deploying to a wide range of applications in WSN. Thus, we proposed a Genetic Algorithm based Multi-Mobile Agents itinerary planning (GA-MIP) to address the problems. The use of GA approach Extensive sim- ulations has been performed to show the better integrated per- formance of GA-MIP.

REFERENCES

[1] K. Romer and F. Mattern, “The design space of wireless sensor net-

works,”IEEE Wireless Communications, vol. 11, no. 6, 2004.

[2] L. Tong, Q. Zhao, and S. Adireddy, “Sensor networks with mobile agents,” in Proceedings of the 2003 IEEE International Conference on Military Communications (MILCOM 2003), Boston, Massachu- setts,USA,2003.

[3] M. Beigl, A. Krohn, T. Zimmer, C. Decker, and P. Robinson, “AwareCon: situation aware context communication,” in Proceed- ings of the 5th IEEE International Conference on Ubiquitous Compu- ting (UbiComp 2003), Seattle, Washington, USA, 2003, pp. 132–139.

[4] L. Shu, Y. Zhang, Z. Yu, L. T. Yang, M. Hauswirth, and N. Xiong,

“Context-aware cross-layer optimized video streaming in wireless multimedia sensor networks,” The Journal of Supercomputing, Springer, 2009.

[5] M. Chen, S. Gonzalez, and V. Leung, “Applications and design issues for mobile agents in wireless sensor networks,” Wireless Communi- cations, IEEE, vol. 14, no. 6, pp. 20–26, 2007.

[6] M. Chen, T. Kwon, Y. Yuan, and V. C. Leung, “Mobile agent based

wireless sensor networks,” Journal of Computers, vol. 1, no. 1, 2006.

[7] M. Chen, T. Kwon, Y. Yuan, Y. Choi, and V. C. M. Leung, “Mobile

agent-based directed diffusion in wireless sensor networks,” EURA- SIP J. Appl. Signal Process., vol. 2007, no. 1, pp. 219–219, 2007.

[8] H. Qi and F. Wang, “Optimal itinerary analysis for mobile agents in

ad hoc wireless sensor networks,” in Proceedings of the IEEE 2001

International Conference on Communications (ICC 2001), Helsinki, Finland, 2001.

[9] M. Chen, V. Leung, S. Mao, T. Kwon, and M. Li, “Energy-Efficient itinerary planning for mobile agents in wireless sensor networks,” in Proceedings of the IEEE 2009 International Conference on Communi- cations (ICC 2009), Bresden, Germany, 2009, pp. 1–5.

[10] Q. Wu, N. S. V. Rao, J. Barhen, S. S. Iyengar, V. K. Vaishnavi, H. Qi,

K. Chakrabarty, S. Member, and S. Member, “On computing mobile agent routes for data fusion in distributed sensor networks,” IEEE Trans. Knowledge and Data Engineering, vol. 16, pp. 740—753, 2004.

[11] M. Chen, S. Gonzlez, Y. Zhang, and V. C. Leung, “Multi-agent itiner-

ary planning for sensor networks,” in Proceedings of the IEEE 2009

International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness (QShine 2009), Las Palmas de Gran Canaria, Spain, 2009.

[12] R. Szewczyk, A. Mainwaring, J. Polastre, J. Anderson, and D. Culler,

“An analysis of a large scale habitat monitoring application,” in Pro- ceedings of the ACM 2004 2nd International Conference on Embed- ded Networked Sensor Systems (SenSys 2004), Boston, MA, USA,

2004, pp. 214–226.

[13] L. Shu, C. Wu, Y. Zhang, J. Chen, L. Wang, and M. Hauswirth, “Net- topo: beyond simulator and visualizer for wireless sensor networks,” ACM SIGBED Review, vol. 5, no. 3, 2008.

[14] M. Mitchell, An Introduction to Genetic Algorithms, 1998. MIT Press. [15] R. Poli and W. B. Langdon, “Schema theory for genetic programming with One-Point crossover and point mutation,” Evolutionary Com-

putation, vol. 6, no. 3, pp. 231–252, 1998.

[16] K. A. D. Jong and W. M. Spears, “A formal analysis of the role of multi-point crossover in genetic algorithms,” Annals of Mathematics and Artificial Intelligence, vol. 5, no. 1, pp. 1–26, Mar 1992.

[17] D. W. W. L. H. K. W. YanWang Zhao, Qianping Jiang, “An agent-

based routing protocol with mobile sink for wsn in coal mine,” in Proceedings of the 3rd International Conference on Pervasive Com- puting and Applications (ICPCA 2008),, Alexandria, Egypt, 2008.

[18] L. Cheng, C. Chen, J. Ma, L. Shu, H. Chen, and L. T. Yang, “Residual time aware forwarding for randomly duty-cycled wireless sensor networks,” in Proceedings of the 7th IEEE/IFIP International Confer- ence on Embedded and Ubiqutious Computing (EUC 2009),, Van- couver, Canada, 2009

http://www.ijser.org