Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 2, Issue 11, Nove mbe r-2011 1

ISSN 2229-5518

Interval Linear Programming with generalized interval arithmetic

G. Ram es h, K. Ganesan

Abstract— Generally, vagueness is modelled by a fuzzy approach and randomness by a stochastic approach. But in some cases, a decision maker may prefer using interval numbers as coefficients of an inexact relationship. In this paper, we define a linear programming problem involving interval numbers as an extension of the classical linear programming problem to an inexact environment. By using a new simple ranking for interval numbers and new generalized interval arithmetic, we attempt to de- velop a theory for solving interval number linear programming problems without converting them to classical linear progra m- ming problems.

Index Terms— Interval Numbers, generalized interval arithmetic, Interval Linear Programming, Ranking

1 INTRODUCTION

——————————  ——————————
N order to solve a Linear Programming Problem, the dec i- sion parameters of the model must be fixed at crisp values. But in real-world applications certainty, reliability and pre- cision of data is often not possible and it involves high infor-
Sengupta et al [3] have reduced the interval number linear pro- gramming problem into a biobjective classical linear programming problem and then obtained an optimal solution. Ishibuchi and Tanaka [12, 13] have defined two types of par-
mation costs. Furthermore the optimal solution of a linear
tial order relations
LR
and
mw between two interval num-
programming problem depends on a limited number of con-
straints and thus some of the information collected are not
useful. Hence in order to reduce information costs and also to construct a real model, the use of interval linear programs are more appropriate.
Linear programming problems with interva l coefficients have been studied by several authors, such as Atanu Sengupta et al. [3] , Bitran [4], Chanas and Kuchta [5], Ishibuchi and Tanaka [12, 13], Lodwick and Jamison [15], Nakahara et al. [16], Steuer [23], Chinneck and Ramadan [6], Herry Suprajitno and Ismail bin Mohd [10] and Tong Shaocheng [24]. Numerous methods for comparison of interval numbers can be found as in Atanu Sengupta [2] etc.
Chanas and Kuchta [5] generalized the known concepts of the solution of linear programming problem with interval
coeﬃcients in the objective function based on preference re-
laions between intervals. Tong Shaocheng [19] reduced the
interval number linear programming problem into two clas-
sical linear programming problems by taking maximum value range and minimum value range inequalities as constraint conditions and then obtained an optimal interval sol ution.
bers. Based on these partial order relations, they have studied
the linear programming problems with interval coefficients in
the objective function, by transforming into a standard bi - objective optimization problem.
Oliveira and Antunes [22] provide an illustrated overview of the state of the art of interval programming in the context of multiple objective linear programming models. Mraz [19] computes the exact upper and lower bounds of optimal values for linear programming problems whose coefficients vary in a given intervals. Hladik [11] computes exact range of the op- timal value for linear programming problem in which input data can vary in some given real compact intervals, and he able to characterize the primal and dual solution sets, the bounds of the objective function resulted from two nonlinear programming problems. Herry Suprajitno and Ismail bin Mohdwe [10] proposed a modification of simplex method for the solution of interval linear programming problems using the software Pascal-XSC.
In general, they have transformed the interval linear pro- gramming problems into one or a series of classical linear pro- gramming problems and then obtained an optimal solution .

 G. Ramesh

Department of Mathematics,

Faculty of Engineering and Technology,

SRM University, Kattankulathur, Chennai - 603203, India

Email: apgramesh@yahoo.com

 K. Ganesan

Department of Mathematics,

Faculty of Engineering and Technology,

SRM University, Kattankulathur, Chennai - 603203, India

Email:ganesank@ktr.srmuniv.ac.in
But in this paper, by using a new method of comparison of generalized interval numbers and a new set of generalized interval arithmetic [7, 8, 17], we develop a simplex like algo- rithm for solving interval linear programming problems with- out converting them to classical linear programming prob- lems.

http :// www.ijser.org

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 2

ISSN 2229-5518

The rest of this paper is organized as follows: In section 2, we

dual(a) = dual([a1, a2]) = [a2 , a1] ]. The opposite of an interval

recall the definition of a new type of arithmetic operations, a

a = [a1, a2] is

opp(a) = opp([a1, a2]) = [-a1 ,- a2] which is the

linear order relation between interval numbers and some re-
additive inverse of
and

1 =  1 , 1  is the multip-

lated results. In section 3, we define interval number linear

a = [a1, a2]

a  a a 

programming problem as an extension of the classical linear programming problem to an inexact environment and prove
licative inverse of

a = [a1, a2]

provided
 1 2 

0 [a1, a2]

some basic results of linear programming problems involving
generalized interval numbers.

2 PRELIMINARIES

The aim of this section is to present some notations, notions and results which are of useful in our further consideration.

2.1 Ranking of Interval Number s

Sengupta and Pal [2] proposed a simple and efficient index for comparing any two intervals on IR through decision maker’s satisfaction. We extend this concept to the set of all genera- lized intervals on KR.

Definition 2.1. Let ° be an extended order relation between

the interval numbers

a = [a1, a2] and

b = [b1, b2] in IR, then

Let

a = [a1, a2] = {x : a1  x  a2 ,x R}. If

a = a1 = a2 = a, then

for m(a) < m(b), we construct a premise (a °

b) which im-

a = [a, a] = a is a real number (or a degenerate interval). Let

IR = {a = [a1, a2] : a1  a2 and a1, a2 R} be the set of all proper

plies that a is inferior to b (or b is superior to a ).

intervals and IR = {a = [a1 , a2] : a1 > a2 and a1, a2  R} be the set

of all improper intervals on the real line R. We shall use the

terms”interval” and”interval number” interchangeably.
An acceptability function A

: KR  KR  [0, )
is defined as:

m(b) - m(a)

A °(a, b) = A (a b) = ,

w here w (b) + w (a)¹¹0.

The mid-point and width (or half-width) of an interval num-

A may be interpreted aswth(be)g+rawd(eao) f acceptability of the “ first

ber

a = [a1, a2]

 a + a
are defined as
  

interval number to be inferior to the second interval number” .

For any two interval numbers a and b in KR, either

m(a) =  1 2

and .

w (a) =  a2 - a1 

 2 

 2 

A (a b)³ ³0 or

A (b a)  ³0 or A (a b) = A (b a) = 0

Algebraic properties of classical interval arithmetic defined on
IR are often insufficient if we want to deal with real world problems involving interval parameters. Because, intervals

and A (a b) + A (b a) = 0.

Also the prposed A - index is transitive; for any three inter-
with nonzero width do not have inverses in IR with respect to
the classical interval arithmetical operations. This ”incom-
val numbers

a, b, c

in KR, if
pleteness” stimulated attempts to create a more convenient interval arithmetic extending that based on IR. In this direc- tion, several extensions of the classical interval arithmetic have

A (a b)³ ³0 and A (b c)³ ³0, then

But it does not mean that

A (a c). .

been proposed. Kaucher [13] proposed a new method, in
which the set of proper intervals is extended by improper in-
tervals and the interval arithmetic operations and functions are extended correspondingly. We denote the set of genera-

A (a c) ³ max{A (a b), A (b °c)}.

If A (a b)³= 0 then we say that the interval numbers a and b

are equivalent (or non-inferior to each other) and we denote it

lized intervals (proper and improper) by

by a  b.

In particular, whenever A (a b)³ 0
and

KR = IR U IR = {[a1, a2] : a1, a2  R}.

w(b)  w(a), then a  b. Also if A (a b) ³ 0 , then we say that

The set of generalized intervals KR is a group with respect to

a ° b and if

A (b a)³ 0

, then we say that b a.

addition and multiplication operations of zero free intervals,
while maintaining the inclusion monotonicity. The algebraic properties of the generalized interval arithmetic create a suita- ble environment for solving algebraic problems involving i n-

2.2 A New Interval Arithmetic

Ganesan and Veeramani [3] proposed new interval arithmetic on IR. We extend this arithmetic operation to the set of genera- lized interval numbers KR and incorporating the concept of
terval numbers. However, the efficient solution of some inter-
val algebraic problems is hampered by the lack of well studied
dual. For

a = [a1, a2], b = [b1, b2]  KR and for , , ·,

,

distributive relations between generalized intervals. Ganesan and Veeramani [7] proposed a new interval arithmetic which satisfies the distributive relations between intervals.
The”dual” is an important monadic operator that reverses the

w e define a * b = [m(a) * m(b) - k, m(a) * m(b) + k],

w here k = min (m(a) * m(b) - α, β - (m(a) * m(b),

 and β are the end points of the interval a  b under the exist- ing interval arithmetic. In pa rticular

end-points of the intervals and expresses an element-to- element symmetry between proper and improper intervals in KR. For a = [a1, a2]  KR , its dual is defined by

(i). Addition :

a + b = [a1 ,a2 ] + [b1 , b2]

= [{m( a) + m(b)} - k, {m( a) + m(b)} + k]

http :// www.ijser.org

w here k = mi n  b2 + a2 ) - (b1 + a1) .

 2 

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 3

ISSN 2229-5518

(ii). Subtraction :

a - b = [a1 ,a2 ] - [b1, b2]

Proposition 2.3. If a, b are two interval numbers with

= [{m( a) - m(b)} - k, {m( a) - m(b)} + k]

w here k = mi n  b2 + a2 ) - (b1 + a1) .

(a - b) 0 , then for any interval number c 0 , we have

ca cb.

 2 

 

A lso if a = b i.e. [a1 , a2] = [b1 , b2], then

Proposition 2.4. For any three interval numbers

a - b = a - dual(a) = [a1 , a2 ] - dual([a1 , a2])

= [a1 , a2 ] - [a2 , a1] = [a1 - a1, a2 - a2] = [0, 0]

(iii). M ultiplication : a b = [a1 , a2 ][b1 , b2 ]

=  a1 + a2   b1 + b2  - w , a1 + a2   b1 + b2  + w 

a = [a1, a2], b = [b1, b2] and

(i) c(a + b)  (ca + cb) and

(ii) c(a - b)  (ca - cb).

c = [c1, c2] , we have

       

 It is to be noted that, if we use the existing multipl ication rule

 2  

2  

2   2 



for interval numbers,

w here w =  β -  α , α α= mi n a b ,a b ,a b ,a b 

  1 1 1 2 2 1 2 2

a b = [a1 , a2][b1, b2] = mi n a1b1,a1b2 ,a2b1,a2b2 ,

 2 

and 

β= max a1b1 ,a1b2 ,a2b1 ,a2b2 

max a1b1 ,a1b2 ,a2b1,a2b2 

the above proposition need not be true. For exa mple, let

A l so i f a = b i .e. [a1 , a2 ] = [b1 , b2 ], then

 

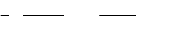
a = -1, 2, b = 2, 5 and c = 2, 3 are any three interval num-

a = a

= a × 1

=[a , a ] × 1

bers. Then by using the existing interval arithmetic, we have

b dual (a)

 
 dual a 

dual ([a1 , a2 ])

(a + b) 

1, 7

and

c(a + b)

2, 21. Also ca

3, 6

and

= [a , a ] × 1

 1 1 

= [a , a ] ×

1 2 [a , a ]

1 2  a a 

cb 

4, 15  (ca + cb) = [1, 21]. So that c(a + b)  (ca + cb).

2 1

 a a 

=  1 2  = [1, 1]

 a1 a2 

 1 2 

3 MAIN R ES ULTS

(iv). Division :

a-1 =[a , a ]1   1

- k,

1 + k  ,

1 2  m(a) m(a) 
In this paper we consider linear programming problems i n-
 
 1  a - a 

1  a - a


volving interval numbers as follows:

w here k = mi n  

2 1  ,

 2 1 

 a2  a1 + a2 

a1  a1 + a2 

Let KR be the set of all generalized interval numbers. Consider the following linear programming problem involving interval

From i i i  , i t i s cl ear that λa =

λa1 , λa2 , for λ 0

λa2 , λa1 , for λ< 0

numbers

maxz   cjx j

j=1

An interval number a is said to be positive if and only if
subject to

 ai jx j

j=1

bi , i = 1, 2, 3… m

, (3.1)

a 0 . That is a 0 and a  [- , α ] for each   0 . Also if

a  0 then a is said to be a zero interval number. It is to be noted that if a  0 , then a  0 , but the converse need not be

and x j  0 for all j=1,2,3,…….,n, where

i = 1,2,3,…….m and j = 1,2,3,……., n.

aij  R, cj , x j , bi  KR, ,

true. If a  0, then a is said to be a non-zero interval number. It is to be noted that if a  0, , then a ¹0 , but the converse need
We call the above problem (3 .1) as an interval number linear programming problem and it can be rewritten as
not be true.

max z  cx

subject to A x b and

x 0,

(3.2)
Now we recall some of the results from [7], which will be us e- ful in proving important theorems.

Proposition 2.1. If a, b are two interval numbers with

(a - b)  0 , then for any interval number c, we have ca  cb.

where A is an (m n) real matrix and b, c, x are (m ×1), (1×n), (n×1) matrices consisting of interval numbers.

Let X = {x = (x1,x2,x3, ......, xn ) : A x b, x 0} be the feasible region of problem (3.1). A feasible solution x*  X , is said to be

Proposition 2.2. If a, b are two interval numbers with

(a - b) 0 , then for any interval number c 0 , we have

ca cb.

an optimum solution to (3.1) if cx³*

c = (c1,c2,c3, ......., cn ) and cx =  cjx j .

j=1

cx for all x  X , where

http :// www.ijser.org

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 4

ISSN 2229-5518

Standard Form:

For the general study, we convert the given interval number linear programming problem into its standard form:

αj + βj >0 , for j=1, 2, 3,…, k;

αj + βj =0 , for j=k+1, k+2,…,n.

max z  cx

subject to A x  b

and

x 0,

(3.3)
That is

x j 0 , for j = 1, 2, 3, · · ·, k;

where A is an (m n) real matrix, b, c, x are (m ×1), (1 ×n), (n×1) matrices consisting of interval numbers.

x j = [-βj , βj ] , for j = k +1, k +2, n, and

 j  0, for all j = 1, 2, 3, · · ·, n.

Now equation (3.4) becomes

Definition 3.1. Let x = (x1 ,x2 ,x3 ,...,xn ).

Suppose x solves

A x  b . If all

x j  [ j , j ] for some  j  0 , then x is said to

 x ja j  [k 1,k 1 ]ak 1  [k  2 ,k  2 ]ak  2  ...  [n ,n ]an  b

j1

be a basic solution. If

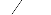
x j  [ j , j ] for some  j  0 , then x has

That is x a +

[-β , β ]a

 b . (3.5)

 j j 

j j j

some non-zero components, say x1,x2,x3, ......, xk , 1  k  n. Then

A x  b can be written as:

j=1 j= k +1

Suppose that the columns

a1 , a 2 , a 3 ,..., a k corresponding to

a1x1 + a 2x 2 + a 3x 3 + ... + a kx k + a k +1[- βk +1 ,βk +1 ]

these positive components

x1 ,x2 ,x3 ,...,xk

are linearly depen-

+ a k + 2[-  βk +2 ,βk +2 ] + ... + a n[-βn,βn]  b

dent, then for atleast one  j  0 (sayr  0 ), we have

k k  θj 

If the columns

a1 , a 2 , a 3 ,..., a k corresponding to these non-

 j a j  0 and hence ar = - θ aj , for j  r .
zero components

x1 , x2 , x3 ,.....,xk

are linearly independent,

j 1

j=1  r 

then x is said to be a basic solution.
Then equation (3.5) becomes

k k    n

 x j

a j 

 j  x

a j 

 [j ,j ] a j  b
Remark 3.1. Given a system of m simultaneous linear equa-

j 1

j 1  r 

j  k 1

tions involving interval numbers in n unknowns (m  n)

j  r j  r

Ax  b,

b KRm , where A is a (m n) real matrix and rank of

k 

 

x j 

j 
 xr 

a j 

 [j ,j ] a j  b
A is m. Let B be any (m m) matrix formed by m linearly in-

j 1 

j  r

k j

r 

 j

j  k 1

 n

 x j - xr 

a j +  x j - xr  a r +

 [, βj ] a j  b

Let x = B-1b = (x ,x ,x ...,x )T

-1

simply we write

j=1 j¹r

r 

k  θj 

r 

j= k +1

x B = B b = (x1 ,x2 ,x3...,xm )

then

x = (x1 ,x2 ,x3 ,...,xm ,0,0,...,0)

That is 

x - x + [-β ,β] +

 [-β ,β]

 b . (3.6)

 j r  a j

r r a r

j j a j

is a basic solution. In this case, we also say that x B is a basic solution.

j=1 j¹r

θr 

j= k +1

  
We are not sure that these variables  x j
  r 

, for j  r are

 r 

Remark 3.2. Consider A x  b where A = (aij )m ××n , aij  R. Then

non-negative. To ensure that these are non -negative, we must

x B =B b is a Solution of A x  b .

have

  
 x j r 
0 , for j=r
Now we are in a position to prove some important theorems
 r 

x  x j 

on interval number linear Programming problems.
Now select r  0 , such that
r  min 

r  j

: x j  0,  j  0  .


Theorem 3.1. If there is any feasible solution to the problem

xr j

r

r 

 j

 j 

(3.3), then there is a basic feasible solution to (3.3).
Then

    

,    
,  

r j 

r r 

 j j 

Proof. Let

x = (x1 ,x2 ,x3 ,......,xn ) be a feasible solution to the

     

  j , j    r , r  0,
by proposition (2.4).
problem (3.3) with the fewest positive components such that

  j

 j 

 r

r 

 

Case (i): If x has no positive components, then x j  [ j , j ] ,
  j

r  j

r 

 j  R,

 j  0

for each j and x is basic by definition.
  

   

  

  j  r   

j  r  

Case(ii): If x has k positive components, say x 1 , x 2 ,
  

    

   j r   j r    0

x 3 ,....., x k , 1  k  n,

then x = (x1 ,x2 ,x3 ,...,xk ,xk +1,...,xn ),

 2 

where x j = [ αj , βj ],

 

 j   j , for j=1, 2, 3,…,n and  

 

http :// www.ijser.org

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 5

ISSN 2229-5518

         

 i j  r r  0  i j
 r  r 

k   j 


  

x  x +

c [ ,  ]
   

    

c j  x j 

xr   cr

 r 

r  r

 j j j

  j
  r 
  j
  r 

j 1 

j  r

r 

 r 

j k 1

 j xr  

 j 

k   j  n

   
 j r 
0   x j 
 r

xr 



0 , for j  r .

  c j

j 1

 x j 
 r

xr  +



 c j [ j ,  j ]

j k 1


Hence each x

 

 j x is positive for j ¹ r and we have a new

  x  

 j  r 

k k

c j x j  

c j j 

c j [ j ,  j ], by proposition (2.4)

 r 

j 1 r j 1

feasible solution with (k - 1) positive variables. That is we have

  j k 1

a new feasible solution with fewer positive components than

 z  x r

 c 
. (3.8)

x has. The new rth component is of the

form -βr ,  βr ,  βr  R , whereas the old rth component xr 0 . k

0 j j r j 1

This contradicts our assumption that x was a feasible solution

If c j  j   j ,  j  ,

j 1

 j  R,
then

z z 0

by taking  r 



 r 
with fewest possible positive components. Therefore the col-
to be some positive or negative interval number. This is a con-
umns

a1 , a 2 , a 3 ,..., a k

are linearly independent. Hence the

tradiction to our assumption that x is optimal. Hence

feasible solution x is basic.

Remark 3.3. It is to be noted that for an interval number linear

 c j  j   j ,  j  , αj  R.

j 1

Then equation (3.8) becomes
programming problem, there are infinite number of basic solu-

z  z0

± -δ δ, δ δ  z0 . The new optimal solution has fewer

tions. But the number of non-equivalent basic solutions is fi- nite.

Proposition 3.1. Let x be a basic feasible solution to problem (3.3) and y is such that (x - y)  0 , then y is also a basic feasi- ble solution to (3.3).

Theorem 3.2. If there is any optimal solution to problem (3.3), then there is a basic optimal solution to (3.3).

positive components than the old optimal solution x. This
contradicts our assumption. Hence the optimal solution x is basic.

Proposition 3.2. Let x is an optimal solution to problem (3.3) and y is such that(x - y)  0 , then y is also an optimal solu- tion to (3.3).

3.1 Improving a basic feasible solu tion

Proof. Let

x  (x1 ,x2 ,x3 ,......,xn ) be an optimal solution to

problem (3.3) with fewest possible positive components and

z 0  cx be the corresponding optimal value.

Let B= (b 1 , b 2 ,..., b m ) form a basis for the columns of A. Let

x = B-1b be a basic feasible solution and the value of the ob-

Case(i) If x has no positive components, then each

x j  [ j , j ] ,  j  R,  j  0 and x is basic by definition.

jective function z is given by

z0  cBx B , where

cB = (cB1,cB2 ,...,cBm ) be the cost vector corresponding to

x B .

Case(ii) If x has k positive components say x1, x2, x3, ......, xk ,

Assume that

a = y b

= y B and the interval number

1  k  n , then

j  ij i j

i =1

x = (x1,x2,x3, ......, xk ,[β- xk +1 , βxk +1],[-βxk +2 ,xk +2β],...,[-βxn , βxn ]) . o

zj = cBy j

are known for every column vector

a j in A, which

k n is not in B. Now we shall examine the possibility of finding

that

 x j a j +

 [- βj , βj ] a j  b

another basic feasible solution with an improved value of z

j=1 j= k +1

The corresponding optimal cost is given by

k n

z0  c j x j   c j [ j ,  j ].

(3.7)
by replacing one of the columns of B by a j .

j 1

j  k 1

Theorem 3.3. Let

x = B-1b be a basic feasible solution to

Since x is an optimal solution with k positive components, it is a feasible solution with k positive components. If x is not a
problem (3.3). If for any column a j in A which is not in B, the
basic feasible solution, then by theorem (3.1), we have a new
condition

(zj - cj ) 0 hold and

yij  0

for some i,


feasible solution with (k 1) positive components x
  j x  ,

i 1,2,3,..,m , 

then it is possible to obtain a new basic feasi-
 j r 
 r 
for j = 1, 2, 3,…, k and j¹ r. The cost corresponding to this new
feasible solution is
ble solution by replacing one of the columns in B bya j . After the replacement of basis vectors, the new basis matrix is
Bˆ = (ˆb , ˆb ,..., ˆb ) , where ˆb = b for i  r and ˆb = a . The

k   j  n

1 2 m i i r j

z*  c  x 

x    c [ ,  ] x

j j r j j j  

j 1 

r 

j k 1

new basic feasible solution is xˆ
, where xˆ

=  x - Br y  ,

j r

B Bi

 Bi


y rj

i j 



http :// www.ijser.org

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 6

ISSN 2229-5518

i  r and xˆ

= xBr

y rj

are the basic variables

4 NUM ERICAL EXAMP LES

Example 4.1

Theorem 3. 4. If x B

= B-1b is a basic feasible solution to prob-

Let us consider an interval linear programming problem given in [5].

lem (3.3) with z0  cBx B
as the value of the objective function

Maximize z =[  20, 50]x + [0, 10]y
and if

xˆ B

is another basic feasible solution with zˆ  ˆc xˆ
ob-

subject to 10x + 60y 1080
tained by admitting a non-basic column vector a j

in the basis
for which

(zj - cj ) 0 and y ij > 0 for some i, i 1,2,3,..,

m ,

10x + 20y 400

then zˆ

z0 .

10x + 10y 240
30x + 10y 420

3.2 Unbou nded solution

We have seen that for a column vector a j of A which is not in

B, for which (zj - cj ) 0 and y ij > 0 , for some i, is alone con-

40x + 10y 520 and x , y 0

Weassume the interval numbers as 1080  [1075, 1085] ,
sidered for inserting into the basis. Let us now discuss the si t-

400  [395, 405],

240  [238,242],

420  [417,423]
and
uation when there exists an a j
such that

(zj - cj ) 0

520  [516, 524]
and y ij  0, for all i = 1, 2, 3,…, m. If

a = [a1 ,a2] 0 and   0 ,

Now the given ILP becomes

then λa = [λa1 , λa2 ] 0 . Now  can be made sufficiently large

so that λa ³b for any interval number b . If λ > 0 , (z j  c j )  0,

Maximize z =[  20, 50]x + [0, 10]y subject to 10x + 60y [1075,1085]

then

 (zj - cj ) 0 .Now the proof of the following theorem

10x + 20y

[395, 405]

follows easily.

Theorem 3.5. Let

x = B-1b be a basic feasible solution to

10x + 10y

30x + 10y

[238, 242] [417, 423]

problem (3.3). If there exist an a j
of A which is not in B such

40x + 10y

[516, 524]

that (zj - cj ) 0 and y ij  0 , for all i,

i 1, 2,3,..., m
then the

and x , y 0

problem (3.3) has an unbounded solution.

3.3 Condition s of Op timality

As in the classical linear programming problems, we can prove that the process of inserting and removing vectors from the basis matrix will lead to any one of the following situa- tions:

(i). there exist j such that (zj - cj ) 0, y ij  0, i = 1, 2, 3,· · ,m or

Using the results proved in this paper, wesolve the ILP as follows:

By introducing non-negative slack variables s1, s2 , s3 , s4 , s5 , the stan- dard form of the given ILP becomes

M axi mi ze z = [ 20, 50]x + [0,10]y

subject to 10x + 60y + s1  [1075, 1085]

10x + 20y + s2  [395, 405]

10x + 10y + s3  [238, 242]

(ii). for all j , (zj - cj ) 0

30x + 10y + s4

 [417, 423]
In the first case, we get an unbounded solution and if the second case occurs, we have an optimal solution.

40x + 10y + s5  [516, 524]

and x, y,s1 ,s2 ,s3 ,s4 ,s5 0.

Theorem 3.6. If

x = B-1b is a basic feasible solution to prob-

That is M aximize z = cx

subject to A x  b

lem (3.3) and if

(zj - cj ) 0 for every column

a j of A, then

and x 0

x B is an optimal solution to (3.3).

where c = ([20, 50] , [0,10], 0, 0 ,0, 0, 0),

http :// www.ijser.org

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 7

ISSN 2229-5518

 x 
Since

(zj - cj ) 0 for all j, the current basic feasible solution is

10 60 1 0 0 0 0
[1075, 1085]

 
  optimal. Theoptimal solution is
10 20 0 1 0 0 0
 [395, 405] 

 s 

   
 1 
s1  [944, 956], s2  [264, 276], s3  [107,113], s4  [24, 36]
A  10 10 0 0 1 0 0 , b =  [238, 242]
 and x  s2 
30 10 0 0 0 1 0
 [417, 423] 
s 
and x  [12.9, 13.1].
   
 3 
40 10 0 0 0 0 1
 [516, 524] 

s 

Example 4.2

Initial iteration:

 

[20, 50] [0,10] 0 0 0 0 0

 
 5 
In daily diet, the quantities of certain foods should be taken to meet certain nutritional requirements at a minimum cost. The consideration is limited to bread, butter and milk and to pro- teins, fats and carbohydrates. The yields of these nutritional requirements per unit of the three types of food are given be-

CB YB XB

x y s1 s2

s3 s4 s5 θ

low:

0 s1

0 s2

0 s3

0 s4

[1075, 1085] 10 60 1 0 0 0 0 [107.5,108.5] [395, 405] 10 20 0 1 0 0 0 [39.5, 40.5] [238, 242] 10 10 0 0 1 0 0 [23.8, 24.2]

[417, 423] 30 10 0 0 0 1 0 [13.9,14.1]

Yield per unit
Food type Proteins Fats Carbohydrates
Bread 4 1 2

0 s5

zj - cj

[516, 524]

[-50, 20]

10 0 0 0 0 1 [-10,0] 0 0 0 0 0

[12.9,13.1]

Butter 3 2 1
Milk 3 2 1
Initial basic feasible solution is given by

s1  [1075, 1085], s2  [395, 405], s3  [238, 242], s4  [417, 423]

and s5  [516, 524].

First iteration:

cj [20,50] [0,10] 0 0 0 0 0

Also one should have 4- 6 grams of proteins, 1- 3 grams of fats and 2- 4 grams of carbohydrates at least every day. The costs of bread, butter and milk may vary slightly from day to day, but are Rs 1- 3 per gram of bread, Rs 8 -10 per gram of butter and Rs 2-4 per gram of milk respectively.
We model this problem as an interval linear programming

CB YB

XB x y s1 s2

s3 s4 s5

θ problem as follows

0 s1

0 s2

0 s3

[944,956] 0 115/ 2 1 0 0 0 -1/ 4 [16.4,16.6] [264,276] 0 35/ 2 0 1 0 0 -1/ 4 [15.1,15.9] [107,113] 0 15/ 2 0 0 1 0 -1/ 4 [14.3,24.2]

minz  [1,3]x1 + [8,10]x2 + [2, 4]x3

subject to 4x1 + 3x 2 + 3x 3 [4,6],

x1 + 2x 2 + 2x 3 [1, 3],

(3.9)

0 s4

[24,36] 0

5/ 2

0 0 0 1 -3/ 4

[9.6,14.4]

2x1 + x 2 + x 3

[2, 4]

[-20,50] x [12.9,13.1] 1 1/ 4 0 0 0 0 1/ 40 [51.6,52.4]

and x1
0, x2
0, x3 0.

(zj - cj ) [0,0]

[-15,12.5]

0 0 0 0 [-0.5,1.25]

By using the theory developed in this paper we obtain an interval optimal solution,
Theimproved basic feasible solution is given by

 52

 11

s1  [944, 956], s2  [264, 276], s3  [107,113], s4  [24, 36]

minz » -10,  = [-10,17.33]

 
with

x1 = -1,  = [-1, 3.67]

 

and x  [12.9, 13.1].

 4 

Second iteration:

[20,50] [0,10] 0 0 0 0 0

x  [0,0] and x3 = - , 2 = [-1.33, 2].

 

5 CONCLUSION

We have proved some of the basic theorems related to interval

CB YB

XB x y s1 s2 s3 s4

s5 θ

linear programming problems using the generalized interval

0 s1

0 s2

0 s3

[116, 404] 0 0 1 0 0 -23 17 [12,108] 0 0 0 1 0 -2.56 5

[-1, 41] 0 0 0 0 1 -3 2

arithmetic. Applying these results, we have developed a simp- lex like algorithm for the interval solution of interval linear programming problems without converting them to classical linear programming problems. Numerical examples are also

[0,10] y [9.6,14.4] 0 1 0 0 0 0.4 -0.3 [-20,50] x [9.3,10.7] 1 0 0 0 0 -0.1 0.1

given to illustrate the theory developed in this paper.

AC KNOWL EDGEM ENT S

(zj - cj )

[0,0] [0,0]

0 0 0 [-5,6] [-5,5]  0

The authors are grateful to the anonymous referees and the editors for their constructive comments and providing refer-

http :// www.ijser.org

International Journal of Scientific & Engineering Research The research paper published by IJSER journal is about Interval Linear Programming with generalized interval arithmetic 8

ISSN 2229-5518

ences.

REFERENCES

[1] G. Alefeld and J. Herzberger, Introduction to Interval Computations, Academic Press, New York 1983.

[2] Atanu Sengupta, Tapan Kumar Pal, Theory and Methodology: On comparing interval numbers, European Journal of Operational Research, 27 (2000), 28 - 43.

[3] Atanu Sengupta, Tapan Kumar Pal and Debjani Chakraborty, Interpretation of inequality constraints involving interval coefficients and a solution to inter- val linearprogramming, Fuzzy Sets and Systems, 119 (2001) 129-138.

[4] G. R. Bitran, Linear multiple objective problems with interval coefficients, Management Science, 26 (1980) 694 - 706.

[5] S. Chanas and D. Kuchta, Multiobjective programming in optimization of interval objective functions - a generalized approach, European Journal of Operational Research, 94 (1996) 594 - 598.

[6] J.W. Chinneck and K. Ramadan, Linear programming with interval coefficients, JORS, 51 (2000) 209 – 220.

[7] K. Ganesan and P. Veeramani, On Arithmetic Operations of Interval Num- bers, International Journal of Uncertainty, Fuzziness and Knowledge - Based Systems, 13 (6) (2005) 619 - 631.

[8] K. Ganesan, OnSome Properties of Interval Matrices, International Journal of

Computational and Mathematical Sciences, 1 (2) (2007) 92 - 99.

[9] E. Hansen, Global Optimization Using Interval Analysis, New York: Marcel

Dekker, 1992.

[10] Herry Suprajitnoand Ismail bin Mohd, Linear Programming with Interval

Arithmetic, Int. J. Contemp. Math. Sciences, Vol. 5, no. 7 (2010) 323 - 332

[11] Hladik M., Optimal value range in interval linear programming, Faculty of

Mathematics and Physics, Charles University, Prague, 2007.

[12] H. Ishibuchi and H. Tanaka, Formulation and analysis of linearprogramming problem with interval coefficients, Journal of Japan Industrial Management Association, 40 (1989) 320 - 329.

[13] H. Ishibuchi and H. Tanaka, Multiobjective programming in optimization of the interval objective function, European Journal of Operational Research, 48 (1990) 219-225.

[14] E. Kaucher, Interval analysis in extended interval space IR, Comput. Suppl. 2 (1980) 33 – 49.

[15] W. A. Lodwick and K. D. Jamison, Interval methods and fuzzy optimization, Int. J. Unccertainty, Fuzziness Knowledge-Based Systems, 5 (1997) 239-249 .

[16] Mohd I.B., A global optimization using interval arithmetic, Journal of Funda- mental Sciences, 2(2006), 76-88.

[17] Mohd I.B., Teori danPenggunaanPengaturcaraanLinear, DewanBahasa dan

Pustaka, Kuala Lumpur, 1991.

[18] R. E. Moore, Method and Application of Interval Analysis, SIAM, Philadelphia, 1979.

[19] Mraz F., Calculating the exact bounds of optimal values in LP with interval coefficients, Annals of Operations Research, 81 (1998) 51 - 62.

[20] Y. Nakahara, M. Sasaki and M. Gen, Onthe linearprogramming withinterval coefficients, International Journal of Computers and Engineering, 23 (1992)

301-304.

[21] T. Nirmala, D. Datta, H. S. Kushwaha and K. Ganesan, Inverse Interval Ma- trix: A New Approach, Applied Mathematical Sciences, 5 (13) (2011) 607 –

624.

[22] Oliveira D. and Antunes C.H., Multiple objective linearprogramming models with interval coefficients - an illustrated overview, EJOR, 181(2007), 1434 –

1463.

[23] R.E. Steuer, Algorithm for linear programming problems with interval objective function coefficients, Mathematics of Operational Research,

6 (1981) 333-348.

[24] Tong Shaocheng, Interval number and fuzzy number linear programming, Fuzzy Sets and Systems, 66 (1994) 301 - 306.

[25] Yager R.R., On the lack of inverses in fuzzy arithmetic, Fuzzy Sets and Sys- tems (1980) 73–82

http :// www.ijser.org