International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1246
ISSN 2229-5518
Infinity in Various Branches of Mathematics
1. Introduction
Infinity (symbolically represented by ∞) is a concept in mathematics and philosophy that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity. In mathematics, infinity is defined in the context of set theory. The word comes from the Latin “infinitas” or “unboundedness”.
While some people conceptualize infinity as a number that is larger than all other numbers, infinity is not treated as a number in mathematics.
The German mathematician Georg Cantor formalized many ideas related to infinity and infinite sets during the late 19th and 20th centuries.
He also discovered that there are different “kinds” or “measures” of infinity, a concept called Cardinality. For example, the set of integers is count ably infinite. However, the set of real numbers is count ably infinite.
Archimedes is the first person known to have discussed extremely large numbers. In his essay “The sand Reckoner”, he built a system on the myriad, the name for 10,000. He called the numbers up to a myriad myriads (100,000,000) numbers of the first order of the first period.
The mathematical symbol of infinity was introduced in 1655 by John Wallis in his Arithmetica infinitorum.
John Wallis (1616-1703) was one of the most original English mathematicians of his day. He was educated for the church at Cambridge and entered Holy orders, but his genius was employed chiefly in the study of mathematics. The Arithmetica infinitorum published in 1655 is his greatest work.
This symbol for infinity is first found in print in his 1655 publication Arithmetica infinitorum. It may have been suggested by the fact that Romans commonly used this symbol for a thousand, just as today the word “myriad” is used for any large number, although in the Greek it meant ten thousand. The symbol was used in expressions such as, in 1695, “Jam numerous incrementorumest (infinity)”.
The symbol for infinity, first chosen by John Wallis in 1655, stands for a concept which has given mathematicians problems since the time of the ancient Greeks. A case in point is that of zeno of Elea (in southern Italy) who, in the 5th century BC, proposed four paradoxes which addressed whether magnitudes
(length or numbers) are infinitely divisible or made up of a large number of small individual parts.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1247
ISSN 2229-5518
2. History
Ancient cultures had various ideas about the nature of infinity. The ancient Indians and Greeks, unable to codify infinity in terms of a formalized mathematical system approached infinity as a philosophical concept.
2.1 Early Indian views of infinity
The Isha Upanishad of yajurveda (4th to 3rd century BC) states that “if you remove a part from infinity or add a part to infinity, still what remains is infinity”.
This is whole, this is whole from the whole, the whole arises. When the whole is taken from the whole, the whole still will remain-Isha Upanishad.
The Indian mathematical text surya prajnapti (C.4000BC) classifies all numbers into three sets:
enumerable, innumerable and infinite.
Each of these was further sub divided into three orders.
• Enumerable: lowest, intermediate and highest.
• Innumerable: nearly innumerable, truly innumerable and innumerably innumerable.
• Infinite: nearly infinite, truly infinite, and infinitely infinite.
The Jains were the first to discard the idea that all infinites were same or equal. They recognized different types of infinities: infinite in length (one dimension), infinite in area (two dimensions), infinite in volume (three dimension), and infinite perpetually (infinite number of dimensions).
According to Singh (1987), Joseph (2000), Agrawal (2000), the highest enumerable number N of Jains corresponds to modern concept of aleph-null 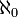 (the cardinal numbers of the infinite set of integers
(the cardinal numbers of the infinite set of integers
1,2,……), the smallest cardinal transfinite number. The Jains also defined a whole system of infinite
cardinal numbers, of which the highest enumerable number N is smallest.
In the Jain work on theory of sets, two basic types of infinite numbers are distinguished. On both physical and onto logical grounds, a distinction was made between asamkhyata(countless) and ananta(endless), between rigidly bounded and loosely bounded infinities.
2.2 Early Greek views of infinity
In accordance with the traditional view of Aristotle, the Hellenistic Greeks generally preferred to distinguish the potential infinity from the actual infinite. For example, instead of saying that there are an infinity of primes, Euclid prefers instead to say that there are more prime numbers than contained in any
given collection of prime numbers.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1248
ISSN 2229-5518
3. Infinity and Its Symbol
In mathematics an unimaginably large value is said to be at infinity or is said to be infinity. For the moment, let us consider such a value to be positive. That is, think of an x number line with the origin, or zero, on it. In your imagination have it extend from zero to the right forever. One could say that infinity is at the end of that line. Except that line has no end. It goes on without end.
So, how far away to the right of zero is positive infinity? Well, if you started at the origin and spent your whole life running toward infinity at a million miles per hour, and somehow miraculously lived for a million lifetimes, at the end of all of that you would be no closer to infinity than when you started.
That puts infinity very far away indeed.
The symbol for this value looks like this: + 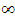
This symbol is often read 'positive infinity'. Just like for normal numbers, the positive sign on infinity can be implied or 'invisible'. Therefore, this symbol has the same meaning: ∞
What about the symbol for negative infinity, that value which is forever distant to the left of the origin?
The symbol looks like this: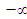
One could think of the positive infinity symbol as a variable with a value that is larger than any other positive number or that is less, in the case of negative infinity, than any negative number.
4. What is Infinity?

Infinity…..
• It’s not big.
• It’s not huge.
• It’s not tremendous large.
• It’s not extremely humungously enormous.
• It’s
Endless!
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1249
ISSN 2229-5518
4.1 Infinity has no end.
• Infinity is the idea of something has no end. In our world we don,t have anything like it. So we imagine traveling on and on, trying hard to get there, but that is not actually infinity.
• So don’t think like that (it just hurts your brain!).just think “endless”, or “boundless”.
• If there is no reason something should stop, then it is infinite.
4.2 Examples
• {1, 2, 3…}: The sequence of natural numbers never ends, and is infinite.
• 1 ∕ 3 is a finite number it is not infinite). But written as a decimal number the digit 3 repeats forever (we say “0.3 repeating”): 0.3333333…….. (etc).
There’s no reason why the 3s should ever stop : they repeat infinitely.
• When you see a number like “0.999…” (i.e. a decimal number with an infinite series of 9s), there is no end to the number of 9s. You cannot say “but what happens if it ends in an 8?”, because it simply does not end. (This is why 0.999… equals to 1).
• AAAA…: An infinite series of “A”s followed by a “B” would NEVER have a “B”.
• There are infinite points in a line. Even a short line segment has infinite points.
4.3 Infinity does not grow
• Infinity is not “getting larger”, it is already fully formed sometimes people say it “goes on and on” which sounds like it is growing somehow. But infinity does not do anything it just is.

Even these faraway galaxies can’t complete with infinity.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1250
ISSN 2229-5518
4.4 Infinity is not a Real Number
• Infinity is not a real number, it is an idea. An idea of something without an end.
• Infinity cannot be measured.
4.5 Infinity is Simple
• Yes, it is actually simple than things which do have an end. Because if something has an end, you have to define where that end is.
Example
In Geometry a “Line” has infinite length…. It goes in both directions without an end.
If it has one end it is called a Ray, and if it has two ends it is called a line segment, but that needs extra information to define where the ends are.
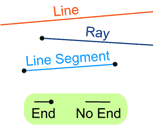
4.6 Big Numbers
There are some really impressively big numbers. A Googol is 1 followed by one hundred zeros (10100)
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,00
0,000,000,000,000,000,000,000.
A Googol is already bigger than the number of elementary particles in the known universe, but then there is the Googolplex. It is 1 followed by Googol zero’s. I can’t even write down the number, because there is not enough matter in the universe to form all the zeros:
10,000,000,000,000,000,000,000,000,000,000,000,000…etc (Googol number of zeros) And there are even larger numbers that need to use “power Towers” to write them down. For example, a Googolplex can be written as this power tower: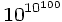 .
.
That is ten to the power of hundred (10 to the power of hundred).
But imagine an even bigger number like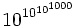 .
.
And you can easily create much larger numbers than those!
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1251
ISSN 2229-5518
4.7 Finite
All of these numbers are “finite”, you could eventually “get there”.
But none of these numbers are even close to infinity. Because they are finite and infinity is …….not finite!
4.8 Using Infinity
We can sometimes use infinity like it is a number, but infinity does not behave like a real number. To help you understand, think “endless” whenever you see the infinity symbol “ :
:
For example: ∞+1=∞ which says that infinity plus one is still equal to infinity.If something is already
endless, you can add 1 and it will still be endless.
The most important thing about infinity is that: -∞ < x < ∞ where x is a real number. Which is mathematical shorthand for “minus infinity is less than any real number, an infinity is greater than any real number”.
4.9 Special Properties of Infinity
∞ + ∞ = ∞, -∞ + -∞ = -∞, ∞ × ∞ = ∞, -∞ × -∞ = ∞, -∞ × ∞ = -∞ x + ∞ = ∞,
x + (-∞) = -∞, x - ∞ = -∞, x - (-∞) = ∞,
For x>0: x × ∞ = ∞ x × (-∞) = -∞
For x<0: x × ∞ = -∞, x × (-∞) = ∞
4.10 Undefined operations
All of these are “undefined”: 0 × ∞, 0 × -∞, ∞ + -∞, ∞ - ∞, ∞ / ∞, ∞0 1∞
4.11 Concepts of Infinity
One of the mysteries of Mathematics seems to be the concept of "infinity", usually denoted by the symbol
∞. So what is ∞? It is simply a symbol that represents large numbers. Indeed, numbers are of three kinds: large, normal size, and small. The normal size numbers are the ones that we have a clear feeling for. For example, what does a trillion mean? That is a very large number. Also numbers involved in macro- physics are very large numbers. Small numbers are usually used in micro-physics. Numbers like 10-75 are very small. Being positive or negative has special meaning depending on the problem at hand. The common mistake is to say that -∞ is smaller than 0. While this may be true according to the natural order
on the real line in term of sizes, -∞ is big, very big!
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1252
ISSN 2229-5518
So when do we have to deal with ∞ and -∞? Easy: whenever you take the inverse of small numbers, you generate large numbers and vice-versa. Mathematically we can write this as 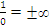 and
and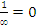 .
.
Note that the inverse of a small number is a large number. So size-wise there is no problem. But we have to be careful about the positive or negative sign. We have to make sure we know whether a small number is positive or negative. 0+ represents small positive numbers while 0- represents small negative numbers. (Similarly, we will use e.g. 3+ to denote numbers slightly bigger than 3, and 3- to denote numbers slightly smaller than 3.) In other words, being more precise we have 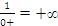 and
and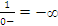 .
.
Remark: Do not treat ± ∞ as ordinary numbers. These symbols do not obey the usual rules of arithmetic, for instance, ∞+1=∞, -1=∞, 2. ∞=∞,etc.
4.12Example. Consider the function f(x)=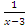 .
.
When x→3, then x-3→0. So 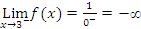 and
and 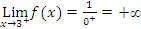
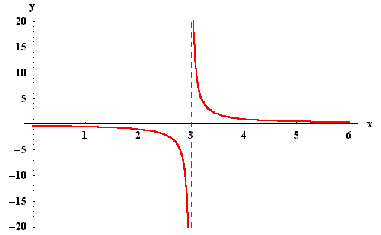
Note that when x gets closer to 3, then the points on the graph get closer to the (dashed) vertical line x=3. Such a line is called a vertical asymptote. For a given function f(x), there are four cases, in which vertical asymptotes can present themselves:
(i)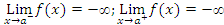 (ii)
(ii) 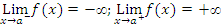
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1253
ISSN 2229-5518
(iii) 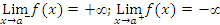 (iv)
(iv) 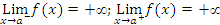
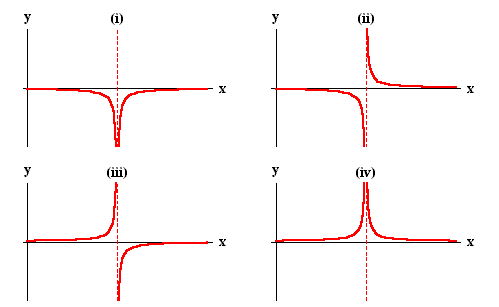
Next we investigate the behavior of functions when x. We have seen that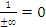 . So for example, we have
. So for example, we have 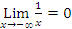 and
and 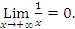
In the next example, we show how this result is very useful.
4.13Example. Consider the function f(x) = 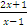 .
.
We have 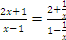 which implies
which implies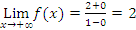 .
.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1254
ISSN 2229-5518
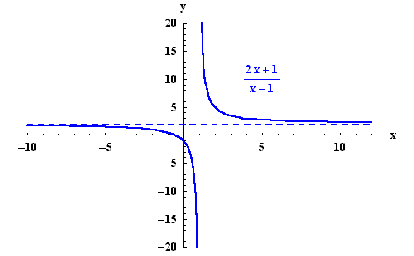
Note that when x gets closer to 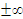 (x gets large), then the points on the graph get closer to the horizontal line y=2. Such a line is called a horizontal asymptote.
(x gets large), then the points on the graph get closer to the horizontal line y=2. Such a line is called a horizontal asymptote.
In particular, we have 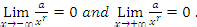 for any number a, and any positive number r, provided xr is defined. We also have
for any number a, and any positive number r, provided xr is defined. We also have 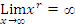
For -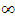 , we have to be careful about the definition of the power of negative numbers. In particular, we have
, we have to be careful about the definition of the power of negative numbers. In particular, we have 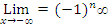 for any natural number n.
for any natural number n.
4.14Example. Consider the function f(x) = 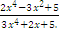
We have 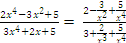
So we have 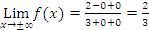
Example: Consider the function f(x)=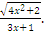
We have 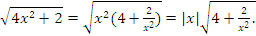 and then
and then 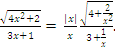
When x goes to + , then x > 0, which implies that |x| = x. Hence 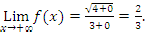
When x goes to 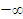 , then x < 0, which implies that |x| = -x. Hence
, then x < 0, which implies that |x| = -x. Hence
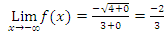
.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1255
ISSN 2229-5518
5. Infinity In Various Branches of Mathematics
5.1 Real analysis
In real analysis, the symbol ∞, called “Infinity”, denotes an unbounded limit. x→∞ means that x grows
without bound, and x→-∞ means the value of x decreasing without bound. If f (t) ≥0 for every t, then
• 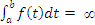 Means that f (t) does not bound a finite area from a to b.
Means that f (t) does not bound a finite area from a to b.
• 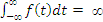 Means that the area under f (t) is infinite.
Means that the area under f (t) is infinite.
• s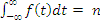 means that the total area under f (t) is finite, and equals to n.
means that the total area under f (t) is finite, and equals to n.
Infinity is also used to describe infinite series:
• 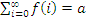 means that the sum of the infinite series converges to some real value a.
means that the sum of the infinite series converges to some real value a.
• 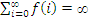 means that the sum of the infinite series diverges in the specific sense that the partial sums grow without bound.
means that the sum of the infinite series diverges in the specific sense that the partial sums grow without bound.
Infinity is often used not only to define a limit but as a value in the affinely extended real number system. Points labeled ∞ and -∞ can be added to the topological space of the real numbers, producing the two- point compactification of the real numbers. Adding algebraic properties to this gives us the extended real numbers. We can also treat ∞ and -∞ as the same, leading to the one-point compactification of the real numbers, which is the real projective line. Projective geometry also introduces a line at infinity in plane geometry, and so forth for higher dimensions.
The extended real number line adds two elements:
Infinity (∞), greater than all other extended real numbers, and negative infinity (-∞), less than all other extended real numbers, for which some arithmetic operations may be performed.
The precise origin of the infinity symbol, ∞ is unclear. One possibility is suggested by the name it is sometimes called- the lemniscates, from the Latin lemniscus, means “ribbon”.
John Wallis is usually credited with introducing ∞ as a symbol for infinity in 1655 in his De-section bus conicis. One conjecture about why he close this symbol is that he derived it from a Roman(number) numeral for 1000 that was in turn derived from the Etruscan(number) numeral for 1000, which looked somewhat like(1) and was sometimes used to mean “ many”. Another conjecture is that he derived it from the Greek letter to (omega), the last letter in the Greek alphabet.
The infinity symbol is available in standard HTML as & in fin; and in Latex as \ infty. In Unicode, it is
the character at code point U+221E, or 8734 in decimal notation.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1256
ISSN 2229-5518
5.2 Complex analysis
These are some of the terms used in the applications of the complex analysis:
• Topological space: let x be a non empty set. A class T of subsets of x is said to be a topology on x. if the following properties are satisfied
a) Ф, x∈T
b) Arbitrary union of sets in T is again a set in T
c) Finite intersection of sets in T is again a set in T
• Complex plane: Every complex number can be represented by a point in the Argand plane.
Let z=x+iy be a complex number by definition z = (x, y). Thus a complex number z is represented by a point p in a plane such a plane is called Argand plane or complex plane.
• Riemann sphere: Representation of a complex number by point of a sphere.
• Pole: f(z) has a pole of order m at z=a if 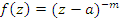 g(z).
g(z).
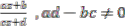
• Meromorphic function: A function which has poles as its only singularities in the finite part of the plane is said to be a meromorphic function.
• Mobius transformation: A mapping of the form s(z)= ,
Here a,b,c,d are complex constants and s,z are complex variables.
As in real analysis, in complex analysis the symbol ∞, called "infinity", denotes an unsigned infinite limit. x→∞ means that the magnitude | x | of x grows beyond any assigned value. A point labeled ∞ can be added to the complex plane as a topological space giving the one-point compactification of the complex plane. When this is done, the resulting space is a one-dimensional complex manifold, or Riemann surface, called the extended complex plane or the Riemann sphere. Arithmetic operations similar to those given below for the extended real numbers can also be defined, though there is no distinction in the signs (therefore one exception is that infinity cannot be added to itself). On the other hand, this kind of infinity enables division by zero, namely 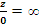 for any complex number z except for zero. In this context it is
for any complex number z except for zero. In this context it is
often useful to consider meromorphic functions as maps into the Riemann sphere taking the value of ∞ at
the poles. The domain of a complex-valued function may be extended to include the point at infinity as well. One important example of such functions is the group of Möbius transformations.
5.3 Non Standard Analysis
The original formulation of infinitesimal calculus by Newton and Leibniz used infinitesimal quantities. In the twentieth century, it was shown that this treatment could be put on a rigorous footing through various logical systems, including smooth infinitesimal analysis and nonstandard analysis. In the latter, infinitesimals are invertible, and their inverses are infinite numbers. The infinities in this sense are part of
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1257
ISSN 2229-5518
a whole field; there is no equivalence between them as with the Cantorian transfinities. For example, if H is an infinite number, then H + H = 2H and H + 1 are distinct infinite numbers. This approach to non- standard calculus is fully developed in H.
5.4 Set Theory
A different form of “infinity” is the ordinal and cardinal infinities of set theory. Georg Cantor developed a system of transfinite numbers, in which the first transfinite cardinal is aleph-null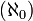 , the cardinality of the set of natural numbers. This modern mathematical conception of the quantitative infinite developed in the late nineteenth century from work by Cantor, Gottlob Frege, Richard Dedekind and others, using the idea of collections, or sets.
, the cardinality of the set of natural numbers. This modern mathematical conception of the quantitative infinite developed in the late nineteenth century from work by Cantor, Gottlob Frege, Richard Dedekind and others, using the idea of collections, or sets.
Dedekind's approach was essentially to adopt the idea of one-to-one correspondence as a standard for comparing the size of sets, and to reject the view of Galileo (which derived from Euclid) that the whole cannot be the same size as the part. An infinite set can simply be defined as one having the same size as at least one of its "proper" parts; this notion of infinity is called Dedekind infinite.
Cantor defined two kinds of infinite numbers, the ordinal numbers and the cardinal numbers. Ordinal numbers may be identified with well-ordered sets, or counting carried on to any stopping point, including points after an infinite number have already been counted. Generalizing finite and the ordinary infinite sequences which are maps from the positive integers leads to mappings from ordinal numbers, and transfinite sequences. Cardinal numbers define the size of sets, meaning how many members they contain, and can be standardized by choosing the first ordinal number of a certain size to represent the cardinal number of that size. The smallest ordinal infinity is that of the positive integers, and any set which has the cardinality of the integers is count ably infinite. If a set is too large to be put in one to one correspondence with the positive integers, it is called uncountable. Cantor's views prevailed and modern mathematics accepts actual infinity. Certain extended number systems, such as the hyper real numbers, incorporate the ordinary (finite) numbers and infinite numbers of different sizes.
6. Infinity in Physics
In physics, approximations of real numbers are used for continuous measurements and natural numbers are used for discrete measurements (i.e. counting). It is therefore assumed by physicists that no measurable quantity could have an infinite value, for instance by taking an infinite value in an extended real number system, or by requiring the counting of an infinite number of events. It is for example presumed impossible for anybody to have infinite mass or infinite energy. Concepts of infinite things
such as an infinite plane wave exist, but there are no experimental means to generate them.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1258
ISSN 2229-5518
6.1 Theoretical Application of Physical Infinity
It should be pointed out that this practice of refusing infinite values for measurable quantities does not come from a priori or ideological motivations, but rather from more methodological and pragmatic motivations. One of the needs of any physical and scientific theory is to give usable formulas that correspond to or at least approximate reality. As an example if any object of infinite gravitational mass were to exist, any usage of the formula to calculate the gravitational force would lead to an infinite result, which would be of no benefit since the result would be always the same regardless of the position and the mass of the other object. The formula would be useful neither to compute the force between two objects of finite mass nor to compute their motions. If an infinite mass object were to exist, any object of finite mass would be attracted with infinite force (and hence acceleration) by the infinite mass object, which is not what we can observe in reality. Sometimes infinite result of a physical quantity may mean that the theory being used to compute the result may be approaching the point where it fails. This may help to indicate the limitations of a theory.
This point of view does not mean that infinity cannot be used in physics. For convenience's sake, calculations, equations, theories and approximations often use infinite series, unbounded functions, etc., and may involve infinite quantities. Physicists however require that the end result be physically meaningful. In quantum field theory infinities arise which need to be interpreted in such a way as to lead to a physically meaningful result, a process called renormalization.
However, there are some theoretical circumstances where the end result is infinity. One example is the singularity in the description of black holes. Some solutions of the equations of the general theory of relativity allow for finite mass distributions of zero size, and thus infinite density. This is an example of what is called a mathematical singularity, or a point where a physical theory breaks down. This does not necessarily mean that physical infinities exist; it may mean simply that the theory is incapable of describing the situation properly. Two other examples occur in inverse-square force laws of the gravitational force equation of Newtonian gravity and Coulomb's Law of electrostatics.
At r=0 these equations evaluate to infinities.
7. Infinity in cosmology
An intriguing question is whether infinity exists in our physical universe: Are there an infinite number of stars? Does the universe have infinite volume? Does space "go on forever"? This is an important open question of cosmology. Note that the question of being infinite is logically separate from the question of having boundaries. The two-dimensional surface of the Earth, for example, is finite, yet has no edge. By travelling in a straight line one will eventually return to the exact spot one started from. The universe, at
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 1259
ISSN 2229-5518
least in principle, might have a similar topology; if one travelled in a straight line through the universe perhaps one would eventually revisit one's starting point.
If, on the other hand, the universe were not curved like a sphere but had a flat topology, it could be both unbounded and infinite. The curvature of the universe can be measured through multiple moments in the spectrum of the Cosmic Background Radiation. As to date, analysis of the radiation patterns recorded by the WMAP spacecraft hints that the universe has a flat topology. This would be consistent with an infinite physical universe. The Planck spacecraft launched in 2009 is expected to record the Cosmic Background Radiation with ten times higher precision, and will give more insight into the question whether the universe is infinite or not.
8. Infinity in Computing
The IEEE floating-point standard specifies positive and negative infinity values; these can be the result of arithmetic overflow, division by zero, or other exceptional operations.
Some programming languages (for example, J and UNITY) specify greatest and least elements, i.e. values that compare (respectively) greater than or less than all other values. These may also be termed top and bottom, or plus infinity and minus infinity; they are useful as sentinel values in algorithms involving sorting, searching or windowing. In languages that do not have greatest and least elements, but do allow overloading of relational operators, it is possible to create greatest and least elements (with some overhead, and the risk of incompatibility between implementations).
IJSER © 2013 http://www.ijser.org
Internatio nal Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013
ISSN 2229-5518
1260
I£ER 2013 http://WWW.ISer.org





