D P
Pe
P e
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 1
ISSN 2229-5518
Heat Transfer in Unsteady Axisymmetric
Rotational Flow of Oldroyd Liquid
A. Mishra, G. S. Ray, S. Biswal
Abstract - This paper deals with the study of heat transfer in unsteady axsymmetric rotational flow of Oldroyd liquid. Constitutive equations of the problem have been developed and solved by applying Laplace transform technique. Expressions for fluid velocity, temperature, skin-friction and rate of heat transfer are obtained. After computerization with the numerical values of fluid parameters, the velocity and temperature profiles are plotted. Numerical values of skin-friction and rate of heat transfer are entered in tables. It is observed that elasticity of the fluid reduces the phase of os cillation and the increase in Prandtl number decreases the temperature of fluid.
Keywords - Heat transfer, rotational flow, Oldroyd liquid.
1. INTRODUCTION
—————————— ——————————
HE literature is replete with copious results of investigations carried out by a large number of researchers on heat transfer by laminar flow of Newtonian and non-Newtonian fluids. Obviously such studies have gained considerable importance in the fields of technology and engineering sciences. Schlichting1 has discussed several cases of exact solutions of heat transfer in viscous fluids. Khamrui2 has analysed the slow steady motion of an infinite viscous fluid due to the rotation of a circular cylinder. Jain3 has studied the problem of heat transfer by laminar flow of elastico-viscous liquids through parallel walls when both the walls are at uniform temperature and Mishra4 has extended the problem to the case when the walls are at linearly varying temperature. Both of them have obtained an approximate solution of the differential equation governing the velocity field by considering the elasticity of the liquid to be small. Earlier to his work of
1965, Mishra5 has also discussed a problem of heat transfer
by laminar elastico-viscous flow through parallel porous walls. Again, Mishra6 studied the problem of heat transfer by laminar flow of an elastico-viscous liquid in a circular cylinder with linearly varying wall temperature. Mishra and Roy7 have analysed the problem of heat transfer by the rotatory flow of an elastico-viscous liquid between two coaxial circular cylinders. Further, the two workers8 have studied the problem of heat transfer by laminar motion of an elastico-viscous liquid between two coaxial circular cylinders due to longitudinal motion of the inner cylinder. Raju and Devanathan9 have analysed the problem of heat transfer in non-Newtonian fluids and laminar flow through concentric annuli with or without suction. Dash and Behera10 have investigated the problem of laminar flow development and heat transfer of a visco-elastic liquid in a
converging channel. Iben11 has considered the non- stationary plane and circular-symmetric flow of a viscous fluid which forms itself within as well as outside a rotating and infinitely long cylinder and obtained a complete analytical solution for any boundary and initial conditions using the method of Laplace transforms. Subsequently, Reismann12 has developed a solution of the problem of two- dimensional axisymmetric rotational flow of a viscous fluid annulus bounded by two concentric circles considering a suitable modified eigenfunction approach. Recently, Mukherjee and Bhattacharya13 have studied the rotational flow of viscous liquid due to the rotation of a circular lamina or by the action of shearing stress along the boundary. Mukherjee and Mukherjee14 have extended the problem of Mukherjee and Bhattacharya to cover a wider class of liquid, namely elastico-viscous liquid, and in particular to observe the effects of elastic elements in the liquid. The steady and the transient components of the velocity field are obtained explicitly. Dash and Biswal15 have studied the heat transfer in the commencement of Couette flow of Oldroyd liquid with heat sources. Development of unsteady Couette flow and heat transfer in Oldroyd liquid with heat sources under different physical situations has also been analysed by the same authors16. Biswal and Pattnaik17 have investigated the problem of commencement of magnetohydrodynamic unsteady Couette flow of Oldroyd fluid through two porous walls when the lower wall suddenly starts oscillating harmonically.
The objective of the present study is to analyse the problem of heat transfer in unsteady axisymmetric rotational flow of Oldroyd liquid.
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 2
ISSN 2229-5518
2. FORMULATION OF THE PROBLEM
The rotational flow of an elastico-viscous liquid due to the time-dependent rotaion of a circular cylinder is studied here. We consider axisymmetric flow of an Oldroyd liquid within a circular cylinder of radius ‘a’. The time-dependent excitation is caused by the prescribed time-dependent angular velocity to the circular cylinder (Fig.1). It is assumed that the liquid responds in circular motion about the centre and hence the motion of a liquid particle is a function of radial co-ordinate r and time t only.
Our investigation is bared on a model of elastico-viscous liquids which remain essentially the rheological properties of
such liquids under common operating conditions. The constitutive equation of such incompressible liquids, introduced by
Oldroyd18, is given by
P ![]()
D P
Pe
P e
ik 1 Dt
ik 1
D
ij ik
jk ij
=20 [eik + 2![]()
eik 22 eij ejk] (2.1)
Dt
1
Where pik = pik +
pik , the stress tensor and eik =![]()
(vi, k + vk, i), the rate of strain – tensor, P is an arbitrary
2
isotropic pressure, ik is the metric tensor of a fixed co-ordinate xi, 0 is the co-efficient of viscosity, 1 is the
D
stress-relaxation time, 2 (<1) is the rate of strain relaxation time and operator
derivative.
The equations governing the flow of Oldroyd liquid are![]()
denotes the convective time
Dt
u
2 v
1 v v ![]()
![]()
(1+1 )
t t![]()
(1+2
t![]()
)
r 2![]()
r r![]()
, (2.2)
r ![]()
And v![]()
p , (2.3)
r r![]()
Where u (r, t) is the velocity component of the liquid in the direction of increasing and v
kinematic co-efficient of viscosity.
0 is the
The admissible boundary conditions corresponding to the specification of time-dependent velocity on the external boundary and at the centre of the circular cylinder are given by![]()
t > 0 : v = v0 eit at r = a
v is finite at r = 0 (2.4a)
where v0 is the representative velocity and is the imposed oscillation. For a liquid at rest for all t < 0, it may be assumed that the initial state of stress is zero. The initial conditions are
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 3
ISSN 2229-5518
t = 0 : v (r, t) =
vr, t ![]()
t
0 , for all r, (2.4b)
Introducing the following non-dimensional parameters![]()
![]()
v v ,![]()
![]()
r r ,![]()
![]()
t t ,
v0 a a
![]()
![]()
1 = 1 , 2 = 2 ,
a 2 a 2
2 pa2
![]()
![]()
a ,
![]()
p
2
Equations (2.2) and (2.3) become (dropping bar)
v
2 v
1 v v ![]()
(1+1
t
v 2 p![]()
![]()
) (1+2
t t![]()
)
r 2![]()
r r![]()
, (2.5)
r ![]()
![]()
, (2.6)
r r![]()
Subject to the boundary and initial conditions t > 0 : v = eit at r =1
v is finite at r = 0 (2.7a)
and
t = 0 :![]()
v v 0 for all r, (2.7b)
t
3. SOLUTION OF THE EQUATIONS:
The equation (2.5) and the boundary condition (2.7a) are subjected to Laplace transform technique under the condition (2.7b) Thus, we obtain![]()
![]()
d u 1 dv p1 1p 1
(3.1)![]()
![]()
![]()
r 2![]()
r r
1
2 p
![]()
v 0 r 2 ![]()
![]()
v 1
p i![]()
at r = 1
Where![]()
v is finite at r = 0 (3.2)
![]()
v v eptdt, Re(p) > 0, (3.3)
0
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 4
ISSN 2229-5518
The solution of equation (3.1) subject to the boundary conditions (3.2) can be written as![]()
p1 1p
Where![]()
v = A (p) 11 r
1
p
(3.4)
A (p) =
I p i
1![]()
p1 1p
(3.5)
1 1
2 p
The inverse Laplace transform of (3.4) is
I r p1 1p pt ![]()
v = 1
2i
i 1
1
p e dp
(3.6)
i p iI
p1 1p
1 p
1
where is greater than the real part of the singularities of the integrand. Evaluation of the above integral requires a knowledge of the nature and location of the singularities of the integrand. It is clear that the integrand
is an integral function of p and has only simple pole at p = i and poles at the zeros (p=pn) of![]()
p1 1p
I1
1
p Q(p) (say)
To find the zeros of the above expression, we put![]()
p1 1p 2
1 2 p
in the expression and it becomes ij1 (), where ’ns are the roots of
(3.7)
J1 () = 0, (3.8) The zeros of Q (p) is then
1 2
2 2 2
P (=Pn) =
21
1 2n
1
![]()
41n
(3.9)
Poles pn (n = 1, 2, 3, ….) are all simple poles when
(1+2 2 )2 <> 41 2
since for the first inequality the poles are all negative real numbers and for the
n n
![]()
![]()
![]()
second one the poles are complex conjugates and all the within the circle p n n
. It may be remarked that
1
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 5
ISSN 2229-5518
2 2 2
the present problem results in a set of double poles
absent in the case of Newtonian fluid.
p n n![]()
when 1
1
41n
which is found
To evaluate the integral (3.6), we first consider the case when all the singularities are simple poles. The residue at the simple pole p = i is
I r i1 i1
i
1 1 i e
I r i1 i1
1 1 i
The residue at the simple p = pn is
2n
J1 n . 2 pn 1
epn t
![]()
R n J1 n
pn i
Where Rn = 1 2 ![]()
1
4 2 2
2 n 1 n
The expression for the velocity profile can be written as![]()
I r i1 i1
it
1 1 i e
v = 2
![]()
I r i1 i1
1 1 i
n 2 pn 1
J1 n p t
![]()
2
n n
pn
i .![]()
n
J1 n
(3.10)
Or, v = vst + vTt, (3.11)
Where vst represents the steady state solution which is essentially made up of the residue contribution from the pole at p = i and vTt represents the transient part arising out of the residues at p=pn. It we put 1 = 2 = 0 in
(3.10), the velocity profile thus obtained is in good agreement with the flow of Newtonian fluid.
For the case of double pole occurring at Pn =
by![]()
n
(n = 1, 2, …), the velocity distribution is given
1![]()
t ![]()
t
M exp n
tNexp n
, (3.12)
v = vst +
n 1 n 1
= vst +
vTt vTt , (3.13)
IJSER © 2011
International Journal of Scientific & Engineering Research Volume2, Issue 9, September-2011 6
ISSN 2229-5518
Where, M[d f(p p+YF,}}
=-Y
N [(r+YF.}<rl)r
![]()
=-Y
f(p)
11(m)(p + iQ)
and m = p(1+ u 1 p)
(1+ u2 p)
The non-dimensional skin-friction on the wall of the circular cylinder is given by
![]()
I
aprtl
't til Ir=l ---
lloVo r=l
![]()
![]()
![]()
n
Where
(3.14)
![]()
![]()
Heat transfer :
IJSER IS) 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 7
ISSN 2229-5518
The temperature field is governed by the equation![]()
T
K 2 T![]()
2
, (3.15)
t Cp r![]()
With the boundary condition t 0 : (r, t) = 0
t > 0 : (0, t) = 1 (3.16)
(a, t) = 0
Introducing the following non-dimensional quantities in addition to those taken previously,![]()
![]()
T T0 ,
Tw T0
C
![]()
P 0 p
r K
Where T is the temperature of the fluid near the disk, Tw is the temperature of the disk and T0 is the temperature of the fluid at r = a
We obtain (dropping the bar)![]()
t
1 2 ![]()
P r 2
, (3.17)
Where, Pr is the Prandtl number. The boundary conditions for temperature remain as before. Taking Laplace transform of equation (3.17), we have
d 2 1![]()
![]()
![]()
r 2 1![]()
S 0 , (3.18)
Pr ![]()
Where the transformed boundary conditions for are![]()
S > 0 : (0, S) =![]()
![]()
1 , (a, s) = 0, (3.19)
S
The solution of equn. (3.18) is![]()
(r, s) =![]()
1 er
S![]()
sp , (3.20)
Now, taking the inverse Laplace transform of (3.20), we get![]()
(r, t) = erfc
P , (3.21)![]()
Where = r
2 t
The rate of heat transfer in given by
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 8
ISSN 2229-5518
Nu = ![]()
d ![]()
dr r 0![]()
r 0
(3.22)
Dropping the bar, we have
Nu = ![]()
1 d
2 t dr r 0
(3.23)
With the help of (3.21), we get![]()
Nu = 1
, (3.24)
t
4. RESULTS AND DISCUSSION: Fluid Flow :
The velocity expressions given in the equations (3.10) and (3.12) contain both stead and transient parts. Elastic elements
1 and 2 influence both the steady and transient part of the solutions. Taking elastic elements zero, the flow characteristics resembles to those of the time-dependent rotation of the circular cylinder in a viscous fluid. Vst represents the oscillatory part
whereas vTt in (3.11) and Tt
in (3.13) represent the transient parts. As t, the transient parts die away exponentially and the
motion finally attains the oscillatory motion about the steady state.
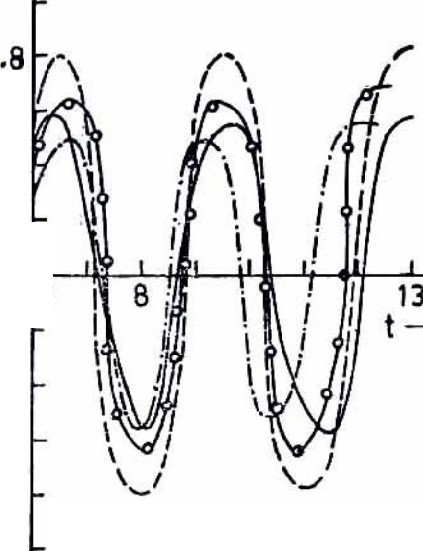
Fig. 2 shows the velocity profiles of Oldroyd liquid for different values of elastic elements 1 and 2 (<1) and also for viscous liquid. It is observed that the effect of elasticity is to diminish the phase of oscillation of the velocity profile i.e., the rate of change of phase of oscillation is quicker in elastic-viscous liquid and the amplitude changes in a parabolic way as in the case of ordinary viscous flow.
Skin-friction:
The effect of elasticity on the skin-friction at the boundary of the cylinder has been presented in the Fig. 3. It is observed that the elastic element increases the skin-friction at any point on the boundary of the circular cylinder. Evidently, for Newtonian fluid (1 and 2 = 0), the values of the shearing stress of the rotational flow are less than those for non-Newtonian fluid (1 and 2 0).
Heat transfer:
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 9
ISSN 2229-5518
The temperature field of the non-Newtonian fluid under consideration has been shown in Fig. 4. It is marked the
increase in Prandtl number decreases the temperature of the fluid. Again, temperature is maximum at the axial region of the cylinder and gradually it falls towards the boundary of the circular cylinder.
Rate of heat transfer:
The rate of heat transfer is characterized by the Nusselt number Nu. The values of the Nusslet number are entered in
Table 1. It is observed that the rate of heat transfer gradually falls with the passage of time.
Table 1 : Values of Nusselt Number
Time t | Nusselt number Nu |
1 | 0.5649 |
2 | 0.3995 |
3 | 0.3261 |
5. CONCLUSIONS
Following conclusions are drawn from the results obtained.
i) The rotational flow of Oldroyd liquid has both oscillatory and transient parts. ii) As t, the transient part die away exponentially.
iii) Both the steady and transient flow are affected by the elastic elements 1 and 2. iv) Elasticity of the fluid reduces the phase of oscillation.
v) The elastic element increases the skin-friction at any point on the boundary of the circular cylinder. vi) The increase in Prandtl number decreases the temperature of the fluid.
vii) The rate of heat transfer decreases as the time passes on.
REFERENCES
1. Schlichting, H., Z.Angew. Math. Mech., 31, 78 (1951)
2. Khamrui, S.R., Bull. Cal. Math. Soc.,47 (1957)
3. Jain, M.K., Appl. Scient. Res., 11A, 295 (1963)
4. Mishra, S.P., Proc. Ind. Acad. Sci., 61A, 219 (1965a)
5. Mishra, S.P., Ind.J.Pure and Appl. Phys.,2, 141-144 (1964)
6. Mishra, S.P., Appl. Sci. Res., 14A, 182-190 (1965b)
7. Mishra, S.P., and Roy, J.S. Proc. Nat. Inst. Sci, India, 35A No.6, 828 (1968)
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 10
ISSN 2229-5518
8. Mishra, S.P., and Roy, J.S. Proc. Nat. Inst. Sci., India, 35A, 816-828 (1969)
9. Raju, K.K. and Devanathan, R. Rheo. Acta, 10, 484-492 (1971)
10. Dash, G.C., and Behera, S.C. Wear, 79, 199-208 (1982)
11. Iben, H.E., ZAMM. 54, No. 5, 215-224 (1974)
12. Reismann, H., ZAMM, 55, 443-45
13. Mukherjee, S., and Bhattacharya, P. Ind.J. Pure and applied Math., 13, No. 10, 1342-1345 (1982)
14. Mukherjee, S., and Kukherjee, S. Ind. J. Pure appl. Math., 14, No. 12, 1534-1541 (1983)
15. Dash, G.C., and Biswal S. Ind. J. Pure appl. Math., 20, No.3, 267-275 (1989)
16. Dash, G.C., and Biswal, S. AMSE J. 48, No.2, 41-64 (1993)
17. Biswal, S., and Pattnaik, B.K. Acta Ciencia Indica, 34P, No.2, 303 (2008)
18. Oldroyd, J.G., Proc. Roy. Soc. London, A200, 523 (1950)
IJSER © 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 11
ISSN 2229-5518
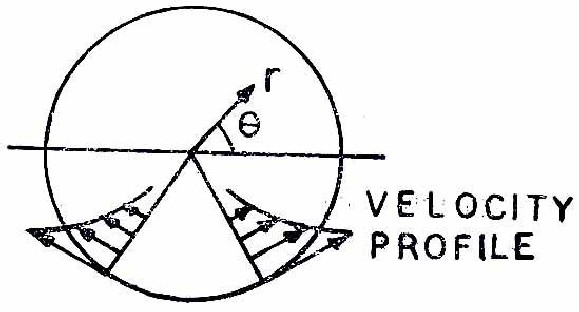
Figure 1 : Sketch of the physical problem (internal flow)
IJSER © 2011
International Journal of Scientific & Engineering Research Volume2, Issue 9, September-2011 12
ISSN 2229-5518
I
> 0 6
-.La
-.8
<X =i
s.o, = 1.1s
--·-«1 = 1 0.01c(2: 4.0
Figure 2 : Velocity profile of elastic viscous and viscous liquid when Q = 2.
IJSER IS) 2011
Interna tional Journal of Scientific & Eng ineering Research Volume2, Issue 9, September-2011 13
ISSN 2229-5518
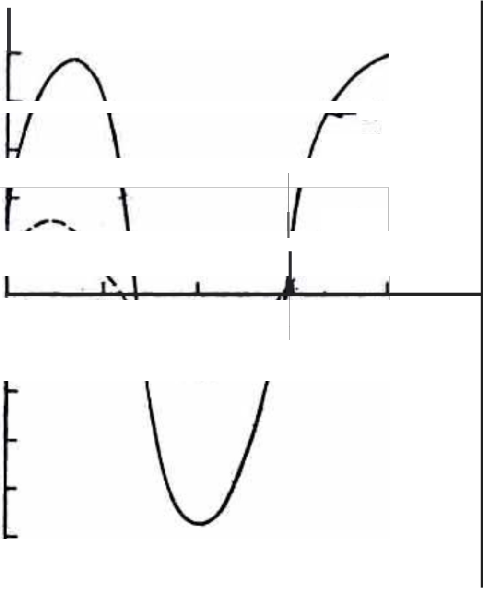
) -----------------------------
2 ol f ; 1
c£ 2 :US
1
.., - ,... o(, = 0
....
0 5 9 10
p t •
-1
-2
Figure 3 : Effect of elastic elements on shearing stress when Q = 2.
IJSER IS) 2011
International Journal of Scientific & Engineering Research Volume 2, Issue 9, September-2011 14
ISSN 2229-5518
Curve Pr
I 2.0
II 4.0
III 6.0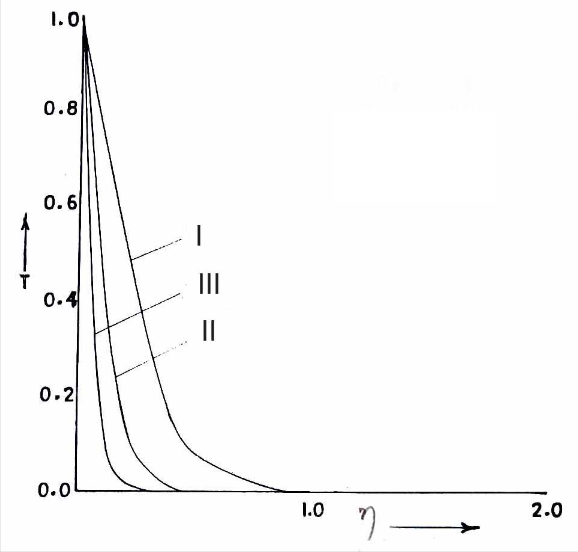
Figure 4 : Transient Temperature Profiles for Different values of Pr, Rc = 0.05, Gr = 5.0
1. Department of Physics, A.D. Mahavidyalaya, Brahmagiri, India
2. P.G. Department of Physics, G.M. Autonomous College, Sambalpur, India
3. Retd. Principal, 193, Jayadeva Vihar, Bhubaneswar, India
IJSER © 2011