International Journal of Scientific & Engineering Research, Volume 4, Issue 8, August-2013 90
ISSN 2229-5518
Heat conduction problem on semi-infinite solid cylinder with heat source
C.M. Jadhav and B.R.Ahirrao
• 1 (C.M. Jadhav)Department of Mathematics, Dadasaheb Rawal College Dondaicha, NMU Jalgaon University, Jalgaon [M.S.], INDIA Email:
• 2(B.R.Ahirrao) Departments of Mathematics, Z.B.Patil College Dhule, NMU Jalgaon University,Jalgaon. INDIA
—————————— ——————————
Tcylinder especially solid cylinder is increasingly
![]()
![]()
![]()
![]()
![]()
∂r2
r ∂r
∂z2 K
K ∂t
HE study of thermal effect on deformation and stresses of
∂2θ + 1 ∂θ + ∂2θ + ξ(r ,z ,y,θ) = 1 ∂T
(2.1)
important. The problem of semi infinite cylinder is more complicated and thus more attractive to many scientists in various modern projects, such as high building, raceway, and container and so on. Astumi et al [9] has discussed the linear thermoelastic problem of infinitely long circular cylinder with a circumference edge crack thermal stresses cause by uniform heat flow distributed by the presence of the crack. The crack
Where ξ(r , z , t, θ) is the internal heat source function, and the![]()
κ = λ , λ being the thermal conductivity of the material, ρ is
ρC
density and C is the capacity
Following [11] use the substitution
ξ(r , z , t, θ) = Φ(r, z, t) + ψ(t)θ(r, z, t) (2.2)
and
t
surface and cylindrical surfaces are insulated. Noda et al [7] has explained the two dimension problem of infinite long circular cylinder whose lateral surface is traction free and
T(r , z , t) = θ(r, z, t)e− ∫0 ψ(y)dy
t
χ(r , z , t) = Φ(r, z, t)e− ∫0 ψ(y)dy
For the sake of brevity, we consider
(2.3)
(2.4)
subjected to an asymmetrical heating is consider within the
context of the theory of generalized thermo elasticity with one
relaxation time. Dos-Sung Lee [3]discussed the three
χ(r , z , t) =
![]()
δ(r−r0)δ(z)
2πr0
e−ωt
, 0 ≤ r0 ≤ b, 0 ≤ z < ∞, ω > 0
(2.5)
dimensional analysis of the stress distribution in long circular
Substitute the equation (2.2) to (2.5) in (2.1), we obtain
cylinder containing a concentric very thin spherical cap cavity![]()
![]()
![]()
![]()
![]()
∂2T + 1 ∂T + ∂2T + χ(r ,z ,t)) = 1 ∂T
(2.6)
.the central plane of cavity is perpendicular to the axis of the
∂r2
r ∂r
∂z2 K
K ∂t
cylinder and the cylinder is subjected to bending .also Kulkarni et al [1]determine the quasi –static thermal stresses in thick circular plate subjected to arbitrary initial temperature on the upper surface with lower surface at zero temperature
where K is the thermal diffusivity of the material of the
cylinder, subjected to the initial condition and boundary
conditions.
T = T0 at t = 0 (2.7)
∂T
and fixed circular edge thermally insulated
In this work we study the thermoelastic problem of semi-![]()
T + k
∂r
∂T
= 0 at r=b , 0 ≤ z < ∞, t>0 (2.8)
infinite solid cylinder with cylindrical surface heat source having constant initial temperature under unsteady-state field. To determine the temperature and thermal stresses by using Hankel and Fourier transform technique.
![]()
= 0 at z=0 , 0 ≤ r < b, t>0 (2.9)
∂z
T = T0 at z → ∞ , 0 ≤ r < b (2.10) Where T = T(r, z, t)
The displacement function in the cylindrical co-ordinate
system are represented by the Goodier’s thermoelastic displacement potential and Love’s function as [4]
∂ϕ ∂2ϕ
Consider a semi-infinite solid cylinder defined 0 ≤ r ≤ b,![]()
![]()
u = − (2.11)
∂r ∂r ∂z
0 ≤ z < ∞, by having constant initial temperature T0
Let (r, φ, z) be cylindrical co-ordinate system and θ be
uz =![]()
∂ϕ + 2(1 − ν)∇2 L −
∂z
∂2L
![]()
∂z2
(2.12)
temperature function of space and time the transient heat conduction equation with internal heat generation is given as
in which Goodier’s thermoelastic potential must satisfy the
equation
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 8, August-2013 91
ISSN 2229-5518
H(µm,β)
+ �T�∗
− H(µm,β)
� e− K(µm +β2)t
![]()
![]()
K(µm2+β2)−ω
2 2
![]()
0 K(µm2+β2)−ω
(3.7)![]()
![]()
![]()
Where ∇2 = ∂ T + 1 ∂T + ∂ T
Applying inverse of Hankel and Fourier Transform we obtain
∂r2
r ∂r
![]()
![]()
∂z2
The component of the stresses are represented by the use of the potential ϕ and Love’s L function as![]()
T(r, z, t) = √2 ∑∞
b
�k1
![]()
µm
2+µm2
1/2
�
J0(µmr)
J0(µb)
![]()
∫β=0 �π
cosβz dβ �Λm,n +![]()
σrr= 2G ��
∂2ϕ
− ∇2 ϕ� +
![]()
∂ �υ∇2L −
![]()
∂2L�� (2.15)
�T�∗ 0 − Λm,n �e− K(µm
2+β2)t
� (3.8)
∂r2
∂z ∂r2
H(µ
,β)
σθθ= 2G ��
1 ∂ϕ
![]()
r ∂r
− ∇2 ϕ� +
![]()
∂ �υ∇2 L −
∂z
![]()
1 ∂L�� (2.16)
r ∂r
= m
K(µm2+β2)−ω
σzz= 2G ��
![]()
1 ∂ϕ r ∂r
− ∇2 ϕ� +
![]()
∂ �υ∇2L −
∂z
1 ∂L
![]()
r ∂r
�� (2.17)
Substitute the value of T(r, z, t) in (2.3), the Temperature
distribution is finally represented by
σrz= 2G �
∂2ϕ
![]()
∂r ∂z
![]()
+ ∂ �(1 − υ)∇2L −
∂r
![]()
∂2L�� (2.18)
∂z
![]()
θ(r, z, t) = √2
∞
m=1
![]()
µm
1/2
![]()
J0(µmr) ∫ �
![]()
cosβz dβ �Λm,n +
Where G and υ are the shear modulus and Poisson’s ratio
b �k12+µm2�
J0(µb)
t
β=0 π
respectively the boundary condition on the traction free
surface functions are σrr= σrr= 0 at r = b (2.19)
Equation (2.1) to (2.19) constitutes the mathematical formation
�T�∗ 0 − Λm,n �e− K(µm
2+β2)t� e∫0 ψ(y)dy (3.9)
of the problem under consideration.
Substitute the value of θ(r, z, t)in (2.13)
ϕ =
We introduce Hankel Transform and its inverse [10]
∞
m=1
ℵ J0 (µmr) ϖ �Λm,n
+ �T�∗ 0
− Λm,n
�e− K(µm
2+β2)t
t
� e∫0 ψ(y)dy
F�(µ ) = b r ′k (µ , r′) F(r′ )dr′
1+ν
![]()
√2 −1
(4.1)
µm
F(r) = ∑∞
k0 (µm , r) F�(µm )![]()
![]()
Where ℵ = � � a
1−ν b (µm
2+β2)
2+µ
![]()
1 ,
2�2
![]()
![]()
Where k (µ , r)=√2
µm
1/2
J0(µmr)
![]()
, and Eigen value µm are ∞
J0(µb)�k1 m
b �k12+µm2�
J0(µb)
![]()
ϖ = ∫ �2 cosβz dβ
β=0 π
positive root of µJ′0 (µb) + k1 J0(µb) = 0
Applying Hankel Transform to (2.3),(2.4),(2.5) , (2.7)and using
(2.6) we obtain
Similarly , for solution for Love’s function
L =![]()
J0(µmr)
![]()
K �−µm 2T�(m, z, t) + φ +![]()
∂2T�(m,z,t)
� + χ�(m, z, t) =
∂T�(m,z,t)
(3.1)
∞
m= J0(µb)
(zcosβz) �Λm,n +![]()
![]()
T� = T�
∂T�
=0
∂r
∂z2
![]()
∂z
(3.2)
�T�∗ 0 − Λm,n �e
− K(µm
2+β2)t
t
� e∫0 ψ(y)dy (4.2)
χ�(m, z, t) = √2 µm
J0(µmr0) δ(z)e−ωt (3.3)
Substitute the value of ϕ and L in (2.11) ,(2.12) resp.
1/2 ∞ ′
b �k12+µm2�
J0(µb)
ur = ∑m=1 ℵµm J 0(µm r) ϖ(1 − zβcosβz − sinβz) �Λm,n +
t
We introduce Fourier Transform and it inverse for region
0 ≤ z < ∞ [10]
∞
�T�∗ 0 − Λm,n �e− K(µm
∞
2+β2)t ∫ ψ(y)dy
F�(β) = ∫ k(β, z′) F(z′)dz′
�∗ − K(µm2+β2)t
z′=0
F(z) = ∞ k(β, z) F�(β)dβ![]()
β=0
uz = � ℵ J0(µm r) ϖ �Λm,n + �T 0 − Λm,n �e �
m=1
Where k(β, z) = �2 cosβz , Eigen value β is positive root of
[ϖ′ − 2(1 − ν)µm
t
2 − zβsinβz − cosβz] e∫0 ψ(y)dy
(4.4)![]()
π
cosβz = 0
K[−µm 2T�∗ (m, β, t) − β2 T�∗ (m, β, t)] + χ�∗ (m, β, t) =![]()
dT�∗(m,β,t)
dz
Using (2.13),(2.14),(4.3) and (4.4) in (2.15),(2.16),(2.17)and (2.18)
the stress functions are obtained as
(3.4)
σrr= 2G ∑∞
ℵ J0 (µm r) ϖ �Λm,n +![]()
dT�∗(m,β,t) + K(µ
dz
2 + β2 )�T∗(m, β, t) = H(µm
, β) (3.5)
�T�∗ 0 − Λm,n �e
− K(µm
2+β2)t
� {ϖ �
−1
![]()
(µm2+β2)
J"0(µm r) + J0 (µm r)� −
Where
H(µm , β) = χ�∗ (m, β, t) =
(µm
1
![]()
2+β2)
[2υβ2cosβz J0 (µm
r)] − [(β + 1)cosβz +![]()
√2 µm
![]()
J0(µmr0) ∞ 2
−ωt
βsinβz]J" (µ r)}e∫t ψ(y)dy (5.1)
b �k 2+µ 1/2
![]()
J0(µb)
∫β=0 �π
cosβz0 dβ e ∞
2 2
which is the first order differential equation and has solution
σθθ= 2G � ℵ J0 (µm r) ϖ �Λm,n + �T�∗ 0 − Λm,n �e− K(µm +β )t�
![]()
T�∗ (m, β, t)e K(µm2+β2)t = H(µm,β)
K(µm2+β2)−ω
(3.6)
At initially t=0
e− K(µm +β2)t + C
m=1
![]()
−1r
{ϖ �
(µm2 + β2 )
J′ (µm
0
r) + J0 (µm
1
r)�
2
C = T�∗0 −
![]()
H(µm,β)
K(µm2+β2)−ω
![]()
−
(µm 2 + β2 )
[2υβ cosβz J0 (µmr)]
t
−[(β + 1)cosβz + βsinβz]r −1 J′ (µmr)}e∫0 ψ(y)dy
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 8, August-2013 92
ISSN 2229-5518
(5.2)
σzz= 2G ∑∞
ℵ J0(µmr) ϖ �Λm,n +![]()
2+β2)t −1
�T�∗ 0 − Λm,n �e− K(µm
� {ϖ �
(µm2+β2)
J"0(µm r) + J0 (µm r)� +
t
[(2υ + β)β2cosβz+β3zsinβz]J0 (µm r)] e∫0 ψ(y)dy
(5.3)
σrz= 2G ∑∞
ℵ J0 (µm r) ϖ �Λm,n +
�T�∗ 0 − Λm,n �e− K(µm
2+β2)t
t
� {ϖ
′ J0(µmr)
+ 2υβsinβz +
β2 sinβz J′ (µm r) e∫0 ψ(y)dy
(5.4)
Setting,
δ(r−r0)δ(z)
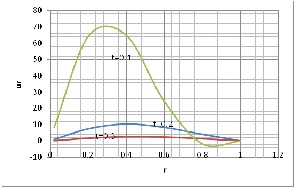
Fig.2 Radical displacement verses radius r with different time
ψ(y) = −y , T0=0 χ(r , z , t) =
2πr0
![]()
e−ωt (6.1)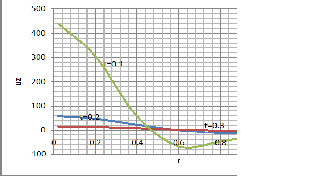
t − t ∗
∫0 ψ(y)dy =
, T� = 0 (6.2)
2
Substitute the value of equation (6.1)and
(6.2)in(3.9),(4.3),(4.4)(5.1)to(5.4)we obtain the expression for the temperature and stresses respectively
θ(r, z, t) = 4 ∑∞
e− K(µm2)tk 2
J0(µmr)J0(µmr0)
− z/4kt
![]()
b2(4πkt)1/2
2
m=1
�k12+µm2�
![]()
J12(µmb) e
�1 −
e− K(µm +β2)t � e− t2/2 (6.3)
Numerical calculation have been carried out for a steel (SN
50C) cylinder with parameter b=1
k1 = 0.5 , z=1, t=1 thermal diffusivity k=15.9, Poisson ratio v =
0281 modulus of elasticity E = 6.9 × 106, shear modulus
G = 2.7 × 106 with µm = 1.0128,1.01234,3.8653, 3.86531,
3.5351, 7.0257, 7.02573, 7.02572, 13.3235, 10.7183 which are the
positive root of µm J′0 (br) + k1J0 (µm b) = 0 and β = 1.5708,
1.5708,-4.7123, 4.7123, 4.7123, 1.5708, 7.2539, 7.2539, 7.2539,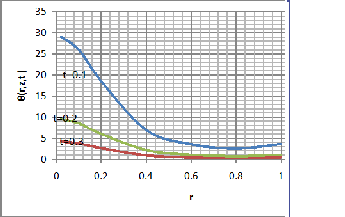
10.9951 are the positive transcendental equation of Cosβz = 0
Fig.1 Temperature distribution verses radius r with different time
Fig.3 Tangential displacement verses radius r with different time
In this paper, we have discussed thermoelastic problem of semi-infinite solid cylinder in which heat source to the cylindrical surface of cylinder and obtained the temperature distribution and stresses we analyze particular case with mathematical model for and numerical calculations were carried out by using Hankel and Fourier transform technique we may calculate that the system of equation in this study can use to design of useful structure of machines in engineering application. Any particular case of special interest can be derived by assigning suitable value of the parameters and function in the expression.
Acknowledgements
The authors express their sincere thanks to Dr. N. W.
Khobragade for their expert comments.
[1] V.S. Kukarni and K.C. Deshmukh, Quasi-static thermal stress in a thick circular plate ,Science Direct ,Applied mathematics modeling
,31(2007),1479-1488
[2] N. Noda, B. Hetnarski, Y. Tanigawa, Thermal stresses second edition ,Taylor and Francis ,New York,2003,259-261
[3] Doo-Sung Lee, Stress distribution in a long cylinder containing
an elliptical crack, Z. Angrew math.mech.(ZAMM),77(1997),701-
709
[4] Hany H. Sherief ,Mohamed N. Anwar ,Two dimensional generalized thermoelastic problem of infinitely long cylinder
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 8, August-2013 93
ISSN 2229-5518
,Journal of thermal stresses ,17(1994),213-227
[5] S. K. Sinha ,Transient temperature distribution in a thick annular disc with transitively anisotropic thermal conductivities
,numerical heat transfer ,Part B Fundamentals ,12(1987),253-261
[6] J. thoms ,J. Singh and D Hesselman, Thermal Stresses in a long circular cylinder subjected to sudden cooling during transient convection heating , Journal of Thermal stresses,8(1985)249-260
[7] N.Noda ,Transient thermoelastic contact problem in a long circular cylinder, Journal of Thermal stresses,1984,135-147
[8] I.N. Snedon, The use of integral transform .McGraw Hill, New
York,1972,235-238
[9] A astimi, Y. Mori and Y. shindo, Thermal stresses in circular cylinder with circumferential edge crack under uniform heat flow , journal of Thermal stresses,2(1679),425-436
[10] N. M. Ozisk, Boundary value problem of heat conduction,
International text book company, Scranton, Pennsylvania, 1968, 135-
148
[11] E .Marchi and A. Fasulo, Alti delta reale academia delle science di jorino1(1967),373
[12] K. R. Gaikwad and K. P. Ghadle ,Quasi-Static Thermoelastic
problem of an infinite long circular cylinder
,J.KSIAM,vol.14,No.3,141-149,2010
[13] Rajneesh Kumar, N.K.Lamba and Vinod Varghese, Analysis of thermoelastic disc with radiation condition on the curved surfaces, Material physics and mechanics 16(2013), 175-186
IJSER © 2013 http://www.ijser.org