International Journal of Scientific & Engineering Research Volume 4, Issue 2, February-2013 1

ISSN 2229-5518

First Principle Pseudopotential Study of

Zinc Blend to Rock Salt Phase Transition in

ZnS

Badal H. Elias1, Nawzat S. Saadi2

Abstract— Using a first-principles pseudopotential approach and the local-density approximation for the exchange correlation potential, we have calculated the equations of state (EOS’s) of the zinc blende (ZB) and rock salt (RS) structures of ZnS. From these EOS’s the high- pressure structural phase transformation of ZnS was investigated. These calculations were showed that the pressure for transition from the ZB structure to the RS structure is 14.93 GPa from normalized primitive cell volume V/V0 –pressure P data, consistent with the experimental data. From the high pressure, we find that the ZB structure ZnS is unstable when the applied pressure is larger than 15 GPa.

Index Terms— Ab-initio calculations, Density functional theory, Electronic structure, High-pressure, Phase Transition, ZnS.

1 INTRODUCTION

——————————  ——————————
nS is one of the prototype IIB-VIA semiconductors. Its cubic form, which occurs naturally as a mineral, has giv- en the name zinc blende to the structure (also known as
sphalerite or B3) in which most IIB-VIA and IIIA-VA semi- conductors crystallize at zero pressure, provided they are not too ionic. At high temperature the hexagonal wurtzite struc- ture, which also has tetrahedral fourfold coordination, is the equilibrium phase and may occur as a metastable form of ZnS at room temperature, as can various polytypes that are inter- mediate between wurtzite and zinc blende. There has been relatively little work on the properties of ZnS at high pressure, but it is known experimentally [1] that at a pressure in the range 15-18 GPa (150-180 kbar) ZnS adopts the rocksalt (NaCI or B1) structure with the sixfold octahedral coordination typi- cal of ionic solids. This transition, which occurs at sufficient pressure for most binary semiconductors, has been treated theoretically for ZnS in some empirical [2] and semiempirical work [3] and in a density functional calculation [4] by Ves et al., and has been studied experimentally in two papers.[4,5]. The ZnS is a wide band gap semiconductor and an attractive material due to its use in various advanced technological ap- plications in infrared optics, ultraviolet laser devices and elec- tronic image displays, etc. Nanobelts, nanoclusters and vari- ous specimens in thin film form have been prepared for this material but the fabrication of large crystal of ZnS is a big problem in many studies due to critical growth condition. Over the past few years, several experimental and theoretical studies have been carried out to understand the mechanical of

————————————————

1. Faculty of Science, School of Physics, Duhok University, Duhok, Iraq. . E-mail: badel_hyder@yahoo.com

2. Faculty of Science, School of Physics, Duhok University, Duhok, Iraq. E-mail: nawzat@uod.ac

ZnS [1-13].
The pressure at which the phase transition from the B3 struc-
ture to the B1 structure for ZnS occurs was first reported as
24.5 GPa [2]. It was estimated to be at 18.5 GPa based on the
shock data of Rice et al. [6]. Zhou et al. [5], using x-ray diffrac-
tion data, reported the phase transition pressure value as 15
GPa. Several research groups have calculated the phase transi-
tions theoretically using different methods recently, Gupta et
al. [14] using ﬁrst principle plane wave pseudopotential (PW-
PP) and full potential linear augmented plane wave method
(FPLAPW) calculation computed the transition pressure value
as 15.2 GPa for (FPLAPW) and 17.2 GPa using (PW-PP) meth-
od, Bilge et al. [15] implemented projector augmented wave pseudo potential formalism (PAW) method to study the phase transition value as 18.5 GPa ,and Chen et al. [7] computed the transition pressure value as 17.5 GPa from total energy–
volume data and 15.4 GPa from equal enthalpies at the transi- tion pressure between two phases.
In this work, we focus on the phase transition of ZnS from the ZB structure (B3) to the RS structure (B1) using a different method. We here adopt a Pseudopotential description of the electron-ion interaction Ultrasoft Pseudopotentials (USP) were introduced by Vanderbilt [8] together with the Perdew–Wang
1991 generalized gradient approximation (GGA) for the ex- change–correlation potential [9] in order to allow calculations to be performed with the lowest possible cutoff energy for the plane-wave basis set, the electronic wavefunctions are ex- panded in a plane-wave basis set with energy cut-off 350 eV. Pseudo-atom calculations are performed for Zn (3d10 4s2) and S (3s2 3p4). As for the Brillouinzone k-point sampling, we use the 12×12×12 Monkhorst–Pack mesh (182 pints), where the self-consistent converged form of the total energy is 5.0×10-7 eV/atom. All electronic structure calculations are implement- ed through the CASTEP code [10-11].
Applying this theory, we have investigated the first order phase transition of ZnS under constant pressure. The rest of this paper is organized as follows: In Section 2, we make a

International Journal of Scientific & Engineering Research Volume 4, Issue 2, February-2013 2

ISSN 2229-5518

brief review of the theoretical method. A detailed description and analysis of our results are presented in Section 3. Finally, a conclusion of the present study is given in Section 4.

2. THEORETICAL METHOD

2.1. Numerical Convergence

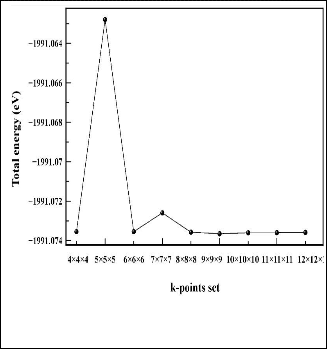
We must determine the cut-off energy for the plane wave basis set and the number of k-points at which to calculate wave- functions. We consider first the truncation of the Fourier series in which the wavefunctions are expanded. We perform a number of simulations at a variety of energy cut-off values, with all other values (such as lattice parameter) kept con- stant.These simulations tell us the total energy of the system, which we can plot versus the cut-off energy used. The results are shown in figure 1. We see that the total energy is a conver- gent monotonically decreasing function of the size of the Fou- rier series used. From these data the cut-off energy of 350eV is achieved for both ZB and RS phases of ZnS. We now consider the discretization of k-space. One of the most popular schemes for generating k-points was proposed by Monkhorst and Pack [12]. This scheme, which was later modified to include hexag- onal systems by Monkhorst and Pack [13], produces a uniform grid of k-points along the three axes in reciprocal space. We freeze all parameters except for the number of k-points used. Again we perform a number of simulations at a variety of k- points set then we plot the total energy against the k-points set. The results are shown in figure 2. Using grid size of

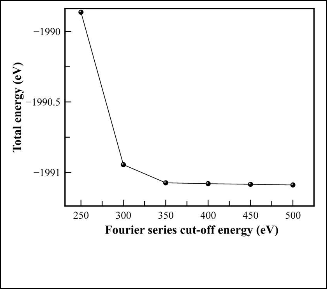
12×12×12 k-points is sufficient to provide results with an error of less than 5.0×10-7 eV/atom for both ZB and RS phases. In our case any further accuracy is not required. And since the computation time required increases with both the above fac- tors, we wish to keep them as low as possible for the desired accuracy. All further simulations have been carried out with the above parameters (i.e. grid size of 12×12×12 k-points and cut-off energy of 350eV).

local pseudopotential introduced by Vanderbilt [8] for the in- teractions of the electrons with the ion cores, together with the generalized gradient approximation (GGA) for exchange- correlation functional in the scheme of Perdew–Burke– Ernzerhof (PBE) [9]. In the present calculations, the electronic wave functions are expanded in a plane wave basis set with energy cut-off of 380 eV, Pseudo-atom calculations are per- formed for Zn (3d10 4s2) and S (3s2 3p4). The K-space integra- tion has been performed using 12×12×12 k points in the irre- ducible Brillouin zone (IBZ), which ensure self-consistent con- vergence differences of the total energy within 5.0×10-7 eV/atom. These parameters are sufficient in leading to well converged total energy and geometrical configurations. All total energy electronic structure calculations are implemented through the CASTEP code [10-11].

Fig. 2. k-space discretisation for ZnS: The total energy of the system plotted against k-points set used in the simulation.

Fig. 1. Fourier series truncation for ZnS: The total energy of the system plotted against the cut-off energy used in the simulation.

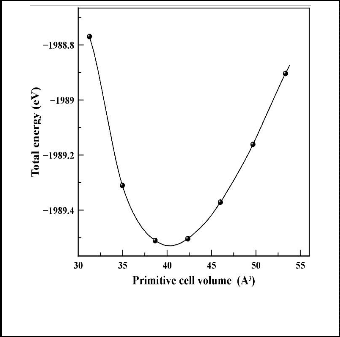
First of all, we make first-principles calculation to find the most stable structure of both the ZB structure and the RS structure of ZnS, we take a series of lattice constants a to ob- tain the total energy E and the corresponding primitive cell volume V, which are illustrated in figure 3. The calculations have been carried out on the primitive cell (9-atom) rather than conventional cell (18-atom) to increase the speed of the calculations.
The calculated total energies and pressures as a function of the primitive unit cell volume for ZnS are used to determine the structural properties, phase behavior and isotropic me- chanical response functions (bulk modulus and its pressure derivative) of ZnS by fitting the data to a third order Birch- Murnaghan equation of states (EOS). In the 3rd order Birch- Murnaghan equation of state (EOS), the total energy and pres- sure as a function of volume are given as [16];

2.2 Total energy and lattice Parameters

E (V )  E

 9V0 B0  V0 3  1 B

'  V0 3  1

6  4( V0 ) 3 
(1)
In all the electronic structure calculation，we adopt the non-

0 16

  V
 0

 V  V 

International Journal of Scientific & Engineering Research Volume 4, Issue 2, February-2013 3

ISSN 2229-5518

and

3.2 Phase transitions

P (V )  3

     3  3
 
1  3 ( B

 4 )
  3  1 
( 2 )
In order to determine the nature of the phase transition in ZnS,

B  V0

V0  

'  V0

  

2  V



V  4 0

  
 V
  
we first plot its pressure-volume curve in Fig. 4. The volume
monotonically decreases with increasing pressure and the ZB
respectively. In these expressions, Eo is the total energy, Vo is
the equilibrium volume, Bo is the bulk modulus at P=0 GPa,
and B' is the first derivative of the bulk modulus with respect
to pressure.
state is still preserved to 14.8 GPa. As the pressure is increased

TABLE 1

THE LATTICE CONSTANTS A (Å), BULK MODULUS B0 (GPA) AND ITS PRESSURE DERIVATIVE B' AND TRANSITION PRESSURES PT (GPA) OF ZNS IN THE B3 AND B1 STRUCTURES AT ZERO PRESSURES.

a b d e

a b d h

Fig. 3. Energy as a function of primitive cell volume of ZB for ZnS.

3. RESULTS AND DISCUSSION

3.1 Structural properties

The ground-state properties of the rock-salt and zincblende structures of ZnS are obtained by the minimization of the total energy, E, with respect to the unit cell volumes, V. We fit the E(V) of ZnS for RS and ZB phases curves to the third-order Birch-Murnaghan equation of states (EOS). It is possible to obtain the equilibrium lattice parameters, zero-pressure bulk modulus and the pressure derivatives of the bulk modulus. The lattice constant a, the bulk modulus B0, its pressure deriv- ative B', and transition pressure (PT) calculated at zero pres- sure are listed in Table1 as well as other theoretical [16, 19, 20,
22, 23, and 25], and experimental data [20, 21, 25, and 26].
We can see that, for the ZB phase, the calculated lattice con-
stant, bulk modulus and its pressure derivatives are in good
agreement with the experimental value and other theoretical.
While for the RS phase, the calculated lattice constant and
bulk modulus are in good agreement with the experimental
and other theoretical value but bulk modulus pressure first
derivative is less than the other calculated and evaluated val- ues but stll in a resonable agreement with the experimental value. We see, from this table, that the calculated value of the transition pressure (PT) is in better agreement with the exper-
imental and other theoretical calculation results.

aRef. [19], bRef. [23], cRef. [24],, dRef. [21], eRef. [25], fRef. [22], gRef. [18], hRef. [16], iRef. [26]

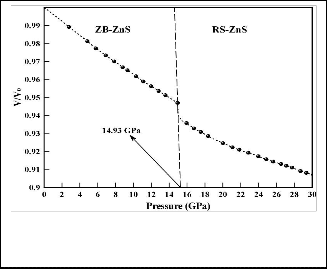
from 14.8 to 15GPa, the structural phase transition begins and is accompanied by a sharp volume drop, which is a character- istic of a first-order phase transition. The structural analysis indicates that the ZB structure converts into a RS structure in excellent agreement with experiments.

Fig. 4 Pressure-volume curve of the ZB ZnS as a function of pressure in constant pressure simulation.

International Journal of Scientific & Engineering Research Volume 4, Issue 2, February-2013 4

ISSN 2229-5518

4. CONCLUSIONS

In summary, first principle calculations based on the density functional theory (DFT) within generalized gradient approxi- mation (GGA) have been performed to investigate the relative stability and the elastic properties of ZnS in the phases of B1 and B3 under different hydrostatic pressures. Our results for lattice parameters are all in agreement with the available ex- perimental and theoretical values at the pressure of 0 GPa. It is shown that the values of the lattice parameter in the phases of B1 and B3 decrease when the pressure is applied to ZnS. The phase transition from B3 to B1 is found as 14.93 GPa accmpa- nying with a volume reduction of about 0.8% which is con- sistent with the other theoretical and experimental data.

ACKNOWLEDGMENT

Authors would like to thank Faculty of Science, School of Physics; Duhok University in carrying out Computations per- formed on Theroritical Physics Group (TPG) computers.

REFERENCES

[1] G. A. Samara and H. G. Drickamer, J. Phys. Chem. Solids 23, 457 (1962)

[2] T. Soma, J. Phys. C 11, 2681 (1978) ; T. Soma and H.-M. Kagaya, Solid

State Commun. 50, 261 (1984)

[3] J. R. Chelikowsy, Phys. Rev. B 35, 1174 (1987)

[4] Kalarasse S. Ves, U. Schwarz, N. E. Christiansen, K. Syassen and M.

Cardona, Phys. Rev. B 42, 9113 (1990)

[5] Y. Zhou, A. J. Campbell and D. L. Heinz, J. Phys. Chem. Solids 52,

821 (1991)

[6] H.G. Drickamer, Rev. Sci. Instrum. 41 (1970) 1667

[7] Chen X Q, Fu C L, Krˇcmar M and Painter G S 2008 Phys.Rev. Lett.

100 196403

[8] Vanderbilt D 1990 Phys. Rev. B. 41 7892

[9] Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 [10] Payne M C, Teter M P, Allen D C, Arias T A and Joannopoulos J D

1992 Rev. Mod. Phys. 64 1045

[11] Milan V, Winker B, White J. A , Packard C J, Payne M C , Akhmat- skaya E V and Nobes R H 2002 Int J. Quantum Chem. 77 85

[12] H.J. Monkhorst and J.D. Pack, Phys. Rev.B 13, 5188 (1976) [13] J. D. Pack and H. J. Monkhorst, Phys. Rev. B 16, 1748 (1977)

[14] S.K. Gupta, S. Kumar, S. Auluck, , Optics Communications, 284 (2011) 20-26

[15] M. Bilge, S. Özdemir Kart, H.H. Kart, T. Cagin, Journal of Achieve- ments in Materials and Manufacturing Engineering , 31, 1, (2008)

29-34

[16] F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev. 71 (1947)

809-824

[17] Catti M 2002 Phys. Rev. B 65 224115 [18] Ves S et al 1990 Phys. Rev. B 42 9113

[19] Jaffe J E, Pandey R and Seel M J 1993 Phys. Rev. B 47 6299

[20] Miao M S and Lambrecht W R L 2005 Phys. Rev. Lett. 94 225501

[21] Chen X R, Li X F, Cai L C and Zhu J 2006 Solid State Commun. 139

246

[22] Chang E and Barsch G R 1973 J. Phys. Chem. Solids 34 1543 [23] Ali Sahraoui F et al 2007 Mater. Lett. 61 1978

[24] Nazzal A and Qteish A 1996 Phys. Rev. B 53 8262

[25] Casali R A and Christense N E 1998 Solid State Commun.108 793 [26] Pan Y et al and Zou G 2002 J. Phys.: Condens. Matter 14 10487