International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 1

ISSN 2229-5518

FPGA Prototyping of Hardware Implementation of CORDIC Algorithm

Er. Manoj Arora, Er. R S Chauhan, Er.Lalit Bagga

Abstract- In 1959 J. E. Volder presents a new algorithm for the real time solution of the equations raised in navigation system. This a lgorithm was the best replacement of analog navigation system by the digital. CORDIC algorithm used for the fast calculation of elementary functions like multiplication, division, trigonometric functions, logarithmic function, and various conversions like conversion of rectangular to polar coordinate, conversion between BCD and binary coded information. In the present time CORDIC algorithm have a number of applications in the field of communic ation, 3-D graphics, signal processing and a lot more. This review paper presents the prototype of hardware implementation of CORDIC algorithm using Spartan –II series FPGA, with constraint to area efficiency and throughput architecture.

Index Terms : CORDIC; FPGA; Discrete Fourier Transform (DFT); Discrete Cosine transform (DCT); Iterative CORDIC; Pipelined CORDIC,SVD.

1 INTRODUCTION

——————————  ——————————
During this period Mr Cochran invent various algorithms and
showed that CORDIC is much better approach for scientific
o-ordinate Rotation Digital Computer is abbreviated as
ORDIC. The main concept of this algorithm is based on the very simple and long lasting fundamentals of two- dimensional geometry. The first description for iterative approach of this algorithm is firstly provided by Jack E. Volder in 1959”[1]”. CORDIC algorithm provides an efficient way of rotating the vectors in a plane by simple shift add operation to estimate the basic elementary functions like trigonometric operations, multiplication, division and some other operations like logarithmic functions, square roots and exponential functions. Most of the applications either in wireless communication or in digital signal processing are based on microprocessors which make use of a single instruction and a bunch of addressing modes for their working. As these processors are costs efficient and offer extreme flexibility but yet are not suited for some of these applications. For most of these applications the CORDIC algorithm is a best suited alternative to that architecture which rely on simple multiply and add hardware. The pocket calculators and some of DSP objects like FFT, DCT, and demodulators are some common fields where CORDIC algorithm is found.
In 1971 CORDIC based computing received attention, when John Walther showed that, by varying a few simple parameters, it could be used as a single algorithm for implementation of most of the mathematical functions.

 Er. Manoj Arora is currently working as head of department and assistant professor in Electronics And Communication Engineering department in JMIT,Radaur (INDIA)

 Er. R. S. Chauhan is currently working as assistant professor in Electronics And Communication Engineering department in JMIT,Radaur (INDIA).E-mail: chauhan@jmit.ac.in

 Er. Lalit Bagga is currently pursuing master’s degree program in Electronics And Communication Engineering from JMIT, Radaur (INDIA). E-mail: lalit.bagga@gmail.com

calculator applications. The popularity of CORDIC is enhanced there after mainly due to its potential for efficient and low-cost implementation of a large class of applications which include the generation of trigonometric, logarithmic and transcendental elementary functions; complex number multiplication, eigenvalue computation, matrix inversion, solution of linear systems and singular value decomposition (SVD) for signal processing, image processing, and general scientific computation. Some other popular and upcoming applications are:
1) Direct frequency synthesis, digital modulation and coding for speech/music synthesis and communication;
2) Direct and inverse kinematics computation for robot manipulation;
3) Planar and three-dimensional vector rotation for graphics and animation.
Although CORDIC algorithm is not a very fast algorithm for
use but this algorithm is followed due to its very simple implementation and also the same architecture can be used for all the applications which is based on simple shift- add operation.

2 CORDIC ALGORTHM

CORDIC is acronym for COordinate Rotation DIgital Computer. The CORDIC algorithm is used to evaluate real time calculation of the exponential and logarithmic functions using the iterative rotation of the input vector. This rotation of a given vector (xi, yi) is realized by means of a sequence of rotations with fixed angles which results in overall rotation through a given angle or result in a final angular argument of zero. Fig1.shows all the computing steps involved in CORDIC algorithm.

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 2

ISSN 2229-5518

In the fig.1 “[1]” the angle αi is the amount of rotation angle
for each iteration and this rotational angle is defined by the following equation:-
α I = tan-12-1 (1)

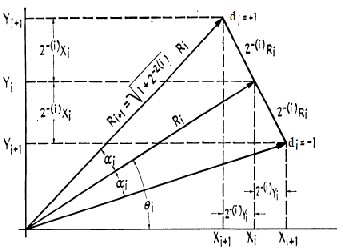
Fig.1 CORDIC computing step

So this angular moment of vector can easily be achieved by
the simple process of shifting and adding. Now if we consider the iterative equation as shown on the next page
xi+1 = xi cos αi – yi sin αi
yi+1 = xi sin αi + yi cosαi (2)
from equation (1), we can write as
xi+1 = cos αi (xi– yi tan αi)
yi+1 = cos αi (xi tan αi + yi )
Now here we define scale factor kn which is same as shown below:
As the value of di depends on the direction of rotation. If we move clockwise then the value of di is +1 otherwise -1.Now these iterations are basically combination of elementary functions like addition , subtraction , shifting and table look up operations and no multiplication and division functions are required in the CORDIC operation.
In CORDIC algorithm, a number of microrotations are combined in different ways to realize some different functions. This is achieved by properly controlling the direction of the successive microrotations. So on the basis of controlling these microrotations we can divide CORDIC in two parts and this control on successive microrotations can be achieved in the following two ways:

Vectoring mode: - In this type of mode the y-component of the input vector is forced to zero. So this type of consideration yields computation of magnitude and phase of the input vector.

Rotation mode: - In the rotation mode θ-component is forced to

zero. and this mode yields computation of a plane rotation of the

input vector by a given input phase θ0 .

2.1 Vectoring mode

As earlier written the in vectoring mode of CORDIC algorithm the magnitude and the phase of the input vector are calculated. The y-component is forced to zero that means the input vector(x0, y0) is rotated towards the x-axis. So the CORDIC iteration in vectoring mode is controlled by the sign of y-component as well as x-component. Means in the vectoring mode the rotator rotates the input vector through any angle to align the result in the x-axis direction.
So in the vectoring mode the CORDIC equations are:
xi+1 = ki [xi + di pi 2-i yi]
Ki = cos αi or 1/√(1+2-2i)
So for the above written two equation we can rewrite them as
yi+1 = ki [yi - di pi 2-i
θi+1 = θi + di pi α i
xi ]
xi+1 = (1/√(1+2-2i) ) Ri cos( αi + θ )
yi+1 = (1/√(1+2-2i) ) Ri cos( αi - θ ) (3)
OR xi+1 = ki (xi - 2-i yi)
yi+1 = ki (yi + 2-i xi )
Now as shown in above equation the direction of rotation
may be clock wise or anticlockwise means unpredictable for different iterations so for that ease we define a binary notation di to identify the direction. It can equal either +1 or -1. So putting di in above equation we get:
xi+1 = ki (xi - di 2-i yi)
yi+1 = ki (yi + di 2-i xi) (4)
where di = sign of x-component
and pi = sign of y-component.
The product of ki’s can be applied elsewhere in the system or
treated as a system processing gain. The product approaches
0.6073 as the number of iterations tends to infinity. Therefore algorithm has a gain An of approximately 1.647. The exact gain depeds upon the number of iterations and follows the relation:
A = ∏ Ki

which provide the following results: Xn = A (√(x02 + y02))
Yn = 0
θn = θ0 + tan-1(y0/x0)

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 3

ISSN 2229-5518

2.2 Rotation mode

In the rotation mode of CORDIC algorithm, with the help of rotation angle say αi we calculate the rotation of the input vector. As the eqation for this mode are :
xi+1 = ki (xi - di 2-i yi) yi+1 = ki (yi + di 2-i xi) θi+1 = θi - di α i
Hence rotations are initialized when the value of θ- component is forced to zero. And after that following rotation based on coomponent di take place:
di = sign(θ) = +1 , x < 0 (clockwise)
-1 , x ≥ 0 (anticlockwise) Usually, a pipeline of adder/subtracters with hardwired shifts is used for high speed CORDIC realizations. the computation time for this architecture is Tc =(N+1).f(N), where f(N) describes the dependence of the propagation delay for addition/ subtraction on the wordlength N.similar. and these equations provide the follllowing result:
Xn = A (x0 cos θ0 - y0 sinθ0) Yn = A (y0 cos θ0 + x0 sinθ0) θn = θ0 + tan-1(y0/x0)
An = ∏ (√ (1+2-2i)

The CORDIC rotation and vectoring algorithms are limited to rotation angle in between ∏/2 to -∏/2. This limitation is due to the use of 20 for the tangent in the first iteration. For composite rotation angles larger than ∏/2, an additional rotation is required. Volder describe the initial rotation of
±∏/2. And the new rotation is as written below:
X’ = - d . x
Y’ = d . y
θ' = θ (if d=1 or z -∏ if d = -1 )
The CORDIC rotator is basically used to evaluate several trigonometric functions directly or indirectly, arctangent, vector magnitude and transformation between rectangular and polar coordinate.

2.3 CORDIC Arithmetic Unit

Fig.2 “[3]” give a simple idea about the CORDIC algorithm. Only shifters, registers and adder / subtractor are used for the calculations. Adder/ subtractor are used for the binary addition and subtraction. Shift registers perform the single bit shifting according to the algorithm. And LUTs (look up tables) are used to set the value of the constants according to the demand of angle setting for the algorithm.
Different hardware is used for computation of sine and cosine

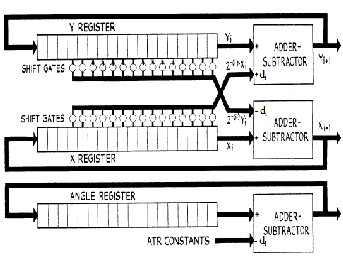
using CORDIC. Here iterative rotations of a point around the origin on the x-y plane are considered. In each rotation, the coordinates of the rotated point and the remaining angle to be rotated are calculated. Since each rotation is a rotation extension the number of rotations for each angle should be a constant independent of operands. So the gain factor K becomes a constant. Hardware implementation for CORDIC arithmetic requires three registers for x, y and z, two shifter to supply the terms 2-i x and 2-i y to the adder/subs tractor units and a look up table to store the values of αi=tan-12-i. The di factor (-1 and 1) selects the shift operand or its complement. The initial inputs to the architectures are X0=1, Y0=0. The structure requires a pre-processing unit to converge the input angles to the desired range and a post processing unit to fix the sign of outputs depending on the initial angle quadrants. The pre-processing unit takes in angles of any range and converges it to the interval [-π/2, π/2]. It keeps record of the quadrant of the input angle which may be used in the post- processing unit to fix the sign of outputs. These two blocks are inevitable for any application as the input range cannot be predicted always

Fig.2 Basic Arithmetic Unit for CORDIC Algorithm

3 CORDIC ARCHITECTURES

Following are the three main architectures used for CORDIC
algorithm:-

3.1 Iterative Architecture

The CORDIC algorithm requires approximately one shift add/ sub operation for each bit of accuracy. A CORDIC core implemented with sequential architectural configuration, implements these shift-add/sub operations serially, using a single shift-add/sub stage and feeding back the output. An iterative CORDIC core with N bit width has a minimum

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 4

ISSN 2229-5518

latency of N cycles. It takes at least N cycles to produce new

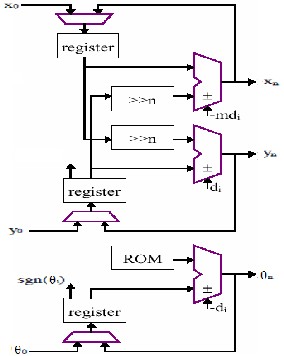
output. The implementation size is directly proportional to the internal precision. This architecture finds major application in pocket calculators, since even a delay of thousands of clock cycles constitute a small fraction of a second for a human user. To obtain sine and cosine values of a given angle z0, iterative structure takes the value of (x0,y0) as (1,0) in the first clock cycle. From the next clock cycle onwards it takes the feedback values and the operation continues till the required output is obtained. The control signal for the input registers is provided by a state-machine designed for the purpose. To get an N bit precise output, the structure requires iterating at least N times. Hence, it requires a minimum of N clock cycles for required output.

Fig.3 Iterative CORDIC

3.2 Higher Radix CORDIC

The generalized equation for a 4-Radix iterative CORDIC
algorithm “[7]” can be written as:
xi+1 = xi - di 4-i yi
yi+1 = yi + di pi 4-i xi
θi+1 = θi - tan-1 di 4-i
where di Є (-2,-1,0,1,2) and tan-1di4-i is elementary angle rotation which is to be performed for each rotation. 4-Radix algorithm reduces the number of iteration to half as compare to the conventional one but increases the hardware complexity. Also there is some problem related to the compensation of scaling factor which can be defined by:
Kn = ∏ Ki = ( 1/√(1+di2 4-2i))
i=0

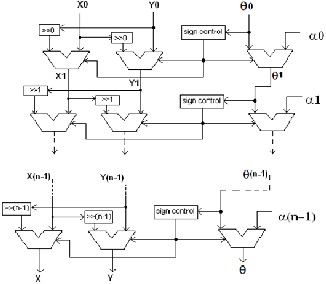
3.3 Parallel or Cascaded Architecture

This architecture uses multiple instances of Iterative CORDIC structure. A CORDIC core with parallel architectural configuration implements the shift-add/sub operations in parallel using an array of shift-add/sub stages. A parallel CORDIC core with N bit output has latency of one clock cycle. The implementation size of a parallel CORDIC core is directly proportional to the internal precision times the number of iterations. Instantiation of blocks must be done N times for an N bit precise output. Unlike in iterative CORDIC, all iterations are done parallelly and hence need not wait for N clock cycles. But, the latency of each block has an inevitable role in fixing the clock frequency. The frequency of operation for Parallel CORDIC core will be lesser than the frequency of operation of iterative CORDIC. But this is the case with a single iteration. While dealing with a chain of inputs, the parallel structure proves to be more efficient one since the throughput of parallel structure is much greater than that of iterative. The shifters used in this structure are constant shifters, which can be implemented in the wiring, so that the hardware can be reduced. So we can llist the following main disadvantages of parallel architecture:
1.) The amount of hardware required is large and the area required is maximum.
2.)Power consumption is highest among the three CORDIC

architectures.

Fig.4 Cascaded Architecture

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 5

ISSN 2229-5518

3.4 Pipelined Architecture

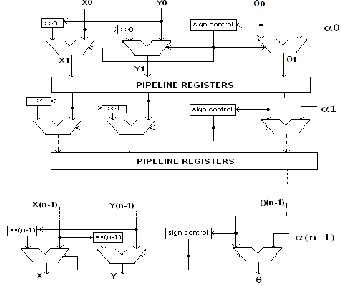
Pipelined architecture uses a structure similar to that of a Parallel CORDIC. It uses pipeline registers in between each iteration phase as shown in Fig.5 ”[4]” Pipelined CORDIC proves to be advantageous with continuous input values. For an N bit data CORDIC core, N stage pipeline can give maximum result. The first output of an N-stage pipelined CORDIC core is obtained after N clock cycles. Thereafter, outputs will be generated during every clock cycle. The advantage of pipelined CORDIC core over parallel and iterative CORDIC cores is its frequency of operation which is much higher when compared to the latter two structures. Pipeline realizes same throughput as that of parallel core with improved frequency of operation. This feature of pipelined structure makes it the best possible option for high frequency satellite communication and other communication systems. A drawback of pipelined structure is the increase in area introduced by the registers. Hence, there is a trade-off between parallel and pipelined cores based on frequency and area. Following are the main advantages of using pipelined architecture:-
1.) FPGA implementation is easy, as registers are already available, thus requiring no extra hardware.
2.) Number of iterations after which the system gives accurate
result can be modelled, considering clock frequency of the system.

3.) When operating at greater clock period power consumption in later stages reduces due to lesser switching activity in each clock period.

Fig.5 Pipelined Architecture

4 FPGA IMPLEMENTATION AND SIMULATION RESULTS

The hardware architecture has been synthesized using Xilinx ISE 8.2i and mapped onto Xilinx XC2s200E-pq 208-5 device. This is a low end FPGA with a small number of logic gates. FPGA implementation details are given in the table 1

Table1

Device Utilization Summary

The simulations results and dataflow model are confirmed to
ModelSim are given below.

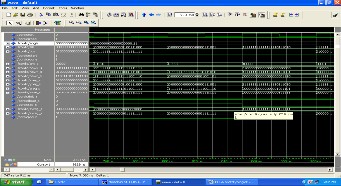
Fig.6. Simulation results

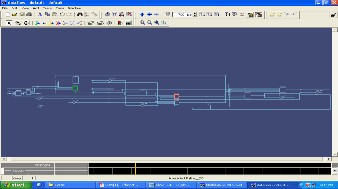
Fig.7 Dataflow Model

5 CONCLUSIONS

The FPGA implementation confirms to CORDIC operation with optimized scheme of slice -delay product for area efficient design.

6 REFERENCES

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 6

ISSN 2229-5518

[1] Jack E. Volder, “The CORDIC trigonometric computing technique,”

IRE Trans. Electron Computers, vol. EC-8, pp. 330–334, Sept. 1959. [2] Jack E. Volder,” The Birth of CORDIC “, Journal of VLSI Signal

Processing 25, 101–105, 2000.

[3] Ramesh Bhakthavatchalu1, Parvathi Nair, Jismi.K, Sinith.M.S, “A Comparison of Pipelined Parallel and Iterative CORDIC Design on FPGA” 2010 5th International Conference on Industrial and Information Systems, ICIIS 2010, Jul 29 - Aug 01, 2010, India

[4] OSKAR MENCER, LUC S ´EM´ERIA AND MARTIN MORF, “Application of Reconfigurable CORDIC Architectures”, Journal of VLSI Signal Processing Systems 24, 211–221, 2000.

[5] Pramod K. Meher, Javier Valls, Tso-Bing Juang, K. Sridharan and Koushik Maharatna, “50 Years of CORDIC: Algorithms, Architectures and Applications” IEEE transactions on circuits and systems—I: regular papers, vol. 56, no. 9, september 2009.

[6] J. Villalba, T. Lang, and E. Zapata, “Parallel compensation of scale

factor for the CORDIC algorithm,” J. VLSI Signal Process., vol. 19, no.

3, pp. 227–241, Aug. 1998.

[7] E. Antelo, J. Villalba, J. D. Bruguera, and E. L. Zapatai, “High performance rotation architectures based on the radix-4 CORDIC algorithm,” IEEE Trans. Computers, vol. 46, no. 8, pp. 855–870, Aug.

1997.

http://www.ijser.org