International Journal of Scientific & Engineering Research, Volume 2, Issue 3, March-2011 1
ISSN 2229-5518
Establishing bridges between UML, HAD and GRAFCET Metamodels for the Modelling of Dynamic Systems
M. Nkenlifack, E. Tanyi and F. Fokou
Abstract— This article shows the scope and limits of UML as a tool for modelling Automatic Control Systems. An alternative metamodel, Hybrid Activity Diagram (HAD), is proposed and applied to a concrete example, in order to illustrate its efficiency in comparison to the limits of UML diagrams. The article also presents bridges which interlink UML, HAD and GRAFCET and establish compatibilities between the three models. Specifications for the development of a HAD simulator and the results obtained from the implementation of the simulator, are also presented in the article.
Index Terms—HAD, UML, Grafcet, Hybrid Dynamic Systems, Modelling and Simulation.
—————————— • ——————————
he Hybrid Activity Diagram (HAD) is a synthesis and fusion of concepts from two domains – Automatic Control Engineering and Software Engineering. The design and implementation of the formalism has been the subject of intense research [1], [2], [3], [4], [5]. The formal- ism is designed to model both the discrete and conti- nuous parts of a system unlike single-paradigm tools like
Grafcet [6] which model only one type of system.
Based on concepts of Object Orientation, HAD is de-
signed to convert UML into a tool which is capable of
modelling hybrid control systems, in order to facilitate
the development of a simulator of such systems. In this
regard, the focus of the article is to outline the design of
HAD, as indicated in [1], [3], and to present its simulator

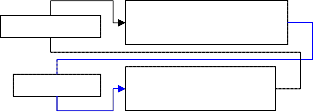
A hybrid dynamic system is one which incorporates both continuous and discrete subsystems. The continuous sub- systems are characterized by continuous-time variables while the discrete subsystems are event-driven and usual- ly sequential in operation. More ample information on such systems can be obtained in [1], [3], [7], [8], [9]). A hybrid dynamic system can, thus, be represented as shown in figure 1.
Continuous System
which is known under the acronym SIMHAD. The func- tionality of SIMHAD is illustrated through an application which models and simulates a liquid-level control system. The model describes the causal relationships governing the operation of the system, the types of signals and the operational conditions of the system.
The primary advantage of the HAD metamodel is con-
Actuator
Sensor
Y’ = <I (Y,t)
Discrete System
If ( x> 0) (…)
vertibility to both UML (Unified Modelling Language) and GRAFCET models through bridges which are de- scribed in the article.
The article is structured in six parts. Section 2 presents the fundamental concepts associated with hybrid systems and UML. The modelling of a liquid-level control system using UML is then presented in section 3 and this serves as a springboard for understanding and defining the properties of HAD. The bridges or mechanisms for con- verting the HAD model into Grafcet and UML Activity Diagram are presented in section 4. The specifications of the hybrid simulator SIMHAD and the results obtained from the simulation of the liquid-level control system are presented in section 5. The last part of the article, section
6, presents the conclusions and perspectives for further work.
Fig. 1. Structure of Hybrid Dynamic Systems [9]
When the logic condition defined on the variable X is true, the actuator immediately triggers the operation (Y’ =
A hybrid dynamic system is, thus, characterized by in- teractions between the continuous and discrete subsys- tems. The evolution of the discrete subsystem from one state to another is predicated on the state of the logic va-
IJSER © 2010
2 International Journal of Scientific & Engineering Research, Volume 2, Issue 3,March-2011
ISSN 2229-5518
![]()
![]()
![]()
riables while the operation of the continuous component is based on physical laws which are usually described by differential or algebraic equations expressing cause-and- effect relationships. However, most of the tools and para- digms developed for the modeling and simulation of dy- namic systems are either continuous or discrete ([1], [3], [8], [10]).
The primary focus of this research project is, therefore, to model and simulate hybrid dynamic systems using the
Unified Modeling Language (UML) which is a universal,
implementation-independent modeling language provid-
ing such properties as modularity, structured program-
ming, re-usability and extensibility [11]. Based on Object
Orientation, UML provides a multiplicity of diagrams
which can be used to define the inheritance of attributes
between related classes of objects as well as relationships
between the components of a system [3], [11] [10].
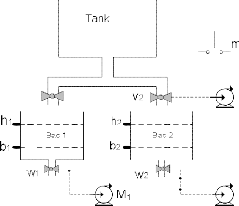
m : push-button to start the system
M : motor
h : maximum level detection sensor b : maximum level detection sensor W and V : valves
TO HIGHLIGHT THE LIMITS OF UML
The system in figure 2 is taken from [12]. Each of the two tanks is fitted with two sensors, one of which detects when the tank is empty and the other detects when the tank is full. Sensor b1, in tank 1, detects when tank1 is empty while sensor h1 detects when the tank is full. Simi- larly, b2 and h2 have the same functions in tank 2. The sensors are, therefore, level-detectors and are modeled as binary rather than continuous variables.
The sequence of operations is as follows:
• Initially, both tanks are empty
• When the operator presses the switch m, the inlet valves V1 and V2 open and the tanks start filling up
• Once a tank is full, the corresponding inlet valve (V1 or V2) closes, to stop filling the tank, and the corresponding outlet valve (W1 or W2) opens, to start evacuating the contents of the tank.
• When a tank is empty, the corresponding out- let valve is closed
When both tanks are empty, the sequence repeats, to start refilling the tanks, when the operator presse the button m.
3.2.1. Analysis of system functionality
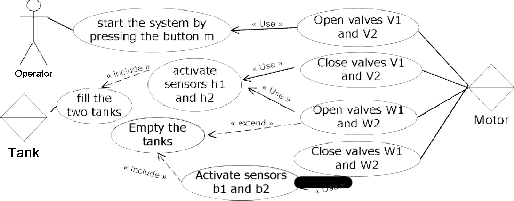
The system functionality described in section 3.1 requires the following Use-cases: starting the system, opening of the valves (V1, V1, W1, W2), activation of the sensors (h1, h2, b1, b2), filling of the tanks and evacuation of the con- tents of the tanks. The actors include the operator, motor and tank, for each filling operation.
Fig. 2. Liquid-level control system [12].
The Use-case diagram (a fundamental UML construct for the description of the functions of a system), which associates the actors to their actions, is shown in figure 3.
This Use-case diagram shows the different sequences and highlights the role of each actor.
3.2.2. Other UML Diagrams required for the Modeling of the System
The Diagram of Classes in figure 4 shows both the static links between the actors as well as the action associated with each link.
The Diagram of Classes in figure 4 describes the attributes of the system components and the communica- tion between them, but it does not describe the sequence of execution of the various tasks, neither does it define the conditions associated with the different tasks as is com- monly the case with control systems modeling tools such as Grafcet and Petri nets. For this reason, Sequence Dia- grams are required to describe the chronology in task execution. However, in order to avoid any ambiguity, more detailed description of the sequences are required.
We consider two scenarios.
1. When the system operator presses the button m, motor
Mo is turned on.
2. When motor Mo reaches its operational speed, it opens the inlet valve V1, to start filling tank 1.
3. When tank 1 is full (h=1), motor Mo reverses its direc- tion of rotation. Mo is, thus, a bi-directional motor.
4. Motor Mo, rotating in the reverse direction, closes the inlet valve V1.
The Sequence Diagram for this sequence of operations is shown in figure 5.
IJSER © 2010
International Journal of Scientific & Engineering Research, Volume 2, Issue 3, March-2011 3
ISSN 2229-5518
![]()
Fig. 3. Use-case diagram of the liquid-level control system
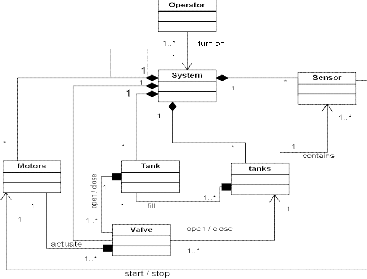
Fig. 4. Diagram of Classes of the liquid-level System
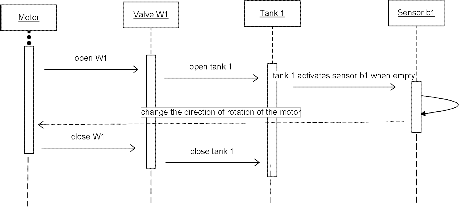
![]()
![]()
Fig. 5. Sequence Diagram for the filling of tank 1
IJSER © 2010
4 International Journal of Scientific & Engineering Research, Volume 2, Issue 3,March-2011
ISSN 2229-5518
1. The activation of sensor h1 (last step in scenario 1)
turns on motor M1
2. Motor M1 opens the outlet valve W1 for evacuation of the liquid
3. When tank 1 is empty (b1=1), motor M1 reverses its
direction of motion
4. The rotation of M1, in the reverse direction, closes valve
W1.
The corresponding Sequence Diagram is shown in figure 6.
The two Sequence Diagrams (figures 5 and 6) provide detailed information on the order in which the different actions are executed during the filling and evacuation of the contents of tank 1. These Sequence-diagrams are also valid for tank 2, by simply substituting the variables of tank 1 with those of tank 2. However, they do not de- scribe sequence selection and simultaneous (parallel) se- quences. The appropriate structure for such sequences is the Activity Diagram [3],[11]. Figure 7 presents the Activi- ty Diagram for the overall system functionality involving the filling and evacuation of the contents of the two tanks.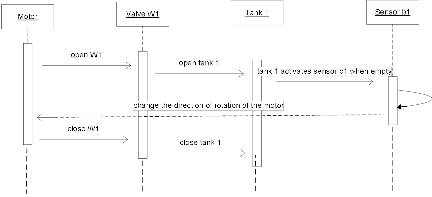
![]()
Fig. 6. Sequence Diagram for the evacuation of the contents of tank 1.
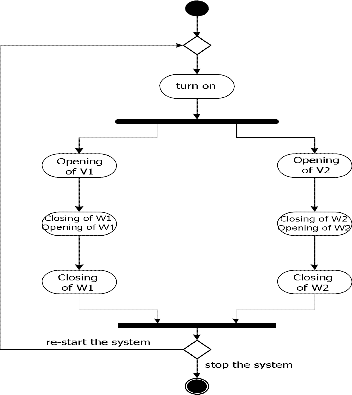
Fig. 7. Activity Diagram for the overall system functionality involving the filling and evacuation of the contents of the two tanks
The diagram in figure 7, in addition to combining the information in figures 5 and 6, shows the conditions for
IJSER © 2010
International Journal of Scientific & Engineering Research, Volume 2, Issue 3, March-2011 5
ISSN 2229-5518
simultaneous and conditional activation of sequences as well as the order of execution of the actions in a sequence. However, the conditions (state of the sensors) driving the sequence from one state to another, are not shown.
The various limits of UML highlighted in its applica- tion to the modeling of the liquid-level system confirm the assertion in [1], [2] that UML does not model the cause-and-effect phenomena in dynamic systems. This
The block diagram in figure 8 regroups and organizes the causes and effects of the system into a single entity. The sensors and push-button "m" are the causes while the valves which are the controlled components are the ef- fects.
m
1
creates the need for the HAD metamodel which allows
sequences to be modeled as Object-oriented entities in- 1
corporating cause-and-effect relationships and the capaci- 2
ty to interchange messages between objects. 2
Inspired by the Activity Diagram [4], [11], [13], HAD is designed to model a system as a collection of localized, autonomous objects having both static and dynamic properties and incorporating a representation of the phys- ical phenomena associated with an object. For the most part, the phenomena are described by differential equa- tions, but algebraic and logic equations are sometimes used.
The opening of a valve requires the actuation of the valve stem by the motor. The motion of the motor, coupled to the valve stem, is described by:![]()
![]()
J t d + Tem - Tr (I)
f r dt f r
And the electromagnetic torque which drives the motor shaft and valve stem is given by :
![]()
W 0
1
b2 W
Fig. 8. Block Diagram for the filling of the two tanks
The corresponding HAD diagram is shown in figure 9. The HAD diagram is an abstract representation of the
filling process and provides a more realistic description of the system since there is greater visibility of the signals (discrete and continuous) interchanged and a better ex- pression of the alternation between the sequential and continuous subsystems. Consequently, it describes the physical phenomenon (through equations ) which govern the behavior of the system. It also facilitates the analysis of the system at three levels : visual, syntaxic and seman- tic. This, in turn, facilitates the development of the simu- lation model.
The bridges are pre-defined rules which are embedded in
T (n )
- (R . nS )n + R nS
![]()
K V
the HAD diagram for the automatic generation of equiva- lent UML or Grafcet models. Since this article is not en-
. .
X 2 n
(nS
X 2 )
nS (R2
X 2 )
(2)
ely devoted to these bridges, only a subset of these
em
Where,
1 . 2 - 2
. n + 2 2 + 2
tir
rules and their implementation will be presented here.
frictional torque constant ;
r
J t is the combined moment of inertia of the motor shaft and load ;
R2 and X 2 are the resistance and reactance of one phase of the motor ;
ns is the synchronous speed
Details of these equations are available in [17].
4.2.1. The HAD – UML Bridge
Table 1 presents an excerpt of the rules for converting a
HAD model to UML.
These rules of conversion have been succesfully tested on several systems ([14], [15], [5]). The application of the rules to the HAD diagram in figure 9 generates the Activ- ity Diagram in figure 10, which conforms to the UML formalism [13].
IJSER © 2010
6 International Journal of Scientific & Engineering Research, Volume 2, Issue 3,March-2011
ISSN 2229-5518
J t d +
T em - T r
dt
r r
T K V
- (R . nS )n + R nS
. .
X 2 n
(nS
X 2 )
nS (R2
X 2 )
em 1
2 . - 2
. 2 n + 2 2 + 2
J t d +
T em - T r J t d +
T em - T r
dt
r
- ( .
r
)n + 2
dt f
r ( ) r 2
2 . R 2 n S
R 2 n S
2 . - R 2. n S n + R 2 n S
T em
K .V 1
X 2 n 2
- 2(n . X
2)n + n 2
(R 2
+ X 2)
T em
K.V 1
X 2 n2
- 2(n .
X 2)n + n2
(R2
+ X 2)
J t d +
dt
r
T em - T r
r
J t d +
T em -T r
- (R 2 . n S
.
)n +
2
R 2 n S
f dt f
T em
K . V 1
2 . 2 - 2(
. 2 ) + n 2 (R 2 + X 2 ) 2
X 2 n
n S X 2 n S 2 2
2 - (R 2. n S )n + R2 n S
T em
K .V 1 .
X 2 n2
- 2(n .
X 2)n + n2
(R2
+ X 2)
Fig. 9. HAD Model for the filling of the two tanks
TABLE 1![]()
![]()
![]()
![]()
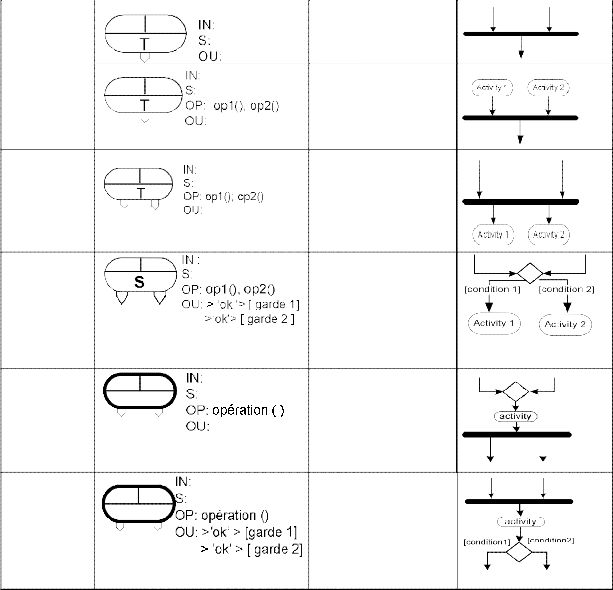
EXCERPT OF THE RULES USED IN CONVERTING HAD MODELS TO UML
Beginning of simultaneous sequences: “AND” - divergence |
. | Object without an opera- tion |
|
Beginning of simultaneous sequences: “AND” - divergence | T | Object with operation (op 1 and op 2 become activity 1 and activity 2 respectively) |
|
![]()
![]()
![]()
![]()
![]()
![]()
IJSER © 2010
International Journal of Scientific & Engineering Research, Volume 2, Issue 3, March-2011 7
ISSN 2229-5518
End of simul- taneous se- quences : “AND” - con- vergence
Object without an opera- tion
Object with operation (op 1 and op 2 become activity 1 and activity 2 respectively)
"AND" - diver- gence and convergence
If there is no operation, the two activities after the bar are deleted
"OR" - divergence
and conver- gence
If there is no operation, the activities which are present are deleted
"OR" - convergence "AND" – divergence
S/T
If there is no operation, the activity which figures on the object is deleted
"AND" - convergence "OR" – divergence
T/S
If there is no operation, the activity which figures on the object is deleted
4.2.2. The HAD – Grafcet Bridge
The HAD-Grafcet bridge is designed to perform a two-stage transformation. The HAD source-code is first transformed into an intermediate model, which is then transformed into Grafcet
Only an excerpt of rules is presented here. More details of the relationships between the two metamodels are pre- sented in [14], [15].
- Eliminate the object which marks the beginning and end of the HAD metagraph
- Eliminate all mathematical equations assigned to the attribute “operation” which describes the dynamics of an object
External influences (ActivityCauses, ActivityEffects)
and internal influences (ActivityClasses) to which the
system is subjected are equivalent to conditions on Graf- cet transitions.
An excerpt of the rules in [14], [15] is presented here. Analyzing the Grafcet from top to bottom :
- Delete all parallel or conditional sequences (se- quence selection) which do not have steps between them ;
- Merge any two consecutive transitions which are not separated by a step
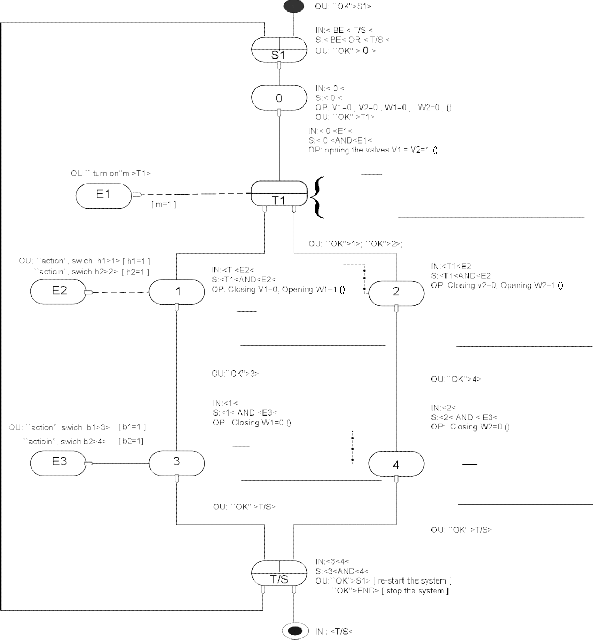
The application of this bridge to the HAD model for the filling of the two tanks generates the Grafcet in figure
11, which conforms to the Grafcet principle of the alternation of steps and transitions.
These models illustrate the fact that HAD models pro- vide greater visibility and abstraction of actions, opera- tions and interchange of signals of a hybrid dynamic sys-
IJSER © 2010
8 International Journal of Scientific & Engineering Research, Volume 2, Issue 3,March-2011
ISSN 2229-5518
tem, compared to the other modeling paradigms used in Automatic Control Engineering. HAD extends UML and adapts it to the requirements of Automatic Control Engi-
neering. This property makes it an interesting tool. In the
next section, we show that its syntax and structure facili- tate the development of software for the simulation of hybrid dynamic systems.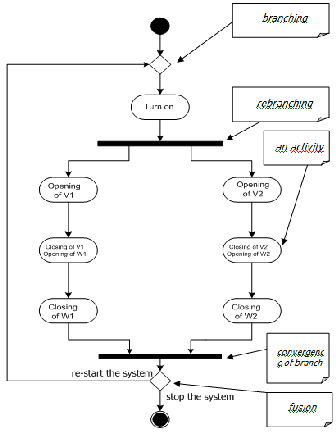
Fig. 10. Activity Diagram generated from the HAD model for the filling of a single tank.
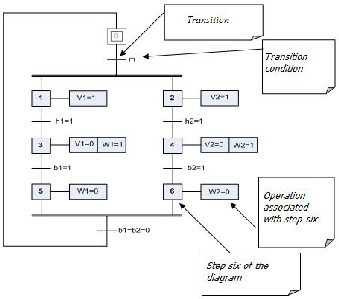
Fig. 11. Grafcet generated from the HAD model for the filling of two tanks,
IJSER © 2010
International Journal of Scientific & Engineering Research, Volume 2, Issue 3, March-2011 9
ISSN 2229-5518
The HAD metamodel has the advantage of being an ex- tension of UML which is widely used in software engi- neering [13]. This is the motivation and justification for the development of a simulator of HAD models.
This aspect requires a specification of dozens of con-
straints. Some of these constraints are highlighted in this section. The full details are available in [14], [15].
5.1.1. Constraints on the Structure of HAD Models
- CH 1: An object is either active or inactive at any giv- en time.
- CH 2: An object is associated with one or more oper- ations.
- CH 3: Two objects communicate through influences ( sending and reception of messages) which are either in- ternal or external.
- CH4: An object can be subjected to internal and ex- ternal influences at the same time. This is a corollary of CH3.
- CH 5: The alternation of transmission and reception of influences must be observed at all times.
- CH 6: The initial and terminal objects must be at the appropriate places.
5.1.2 Contraints on the interconnection of objects:
-CH 7: The ActivityCause – ActivityClass or Activity- NoEffect must be represented as horizontal dotted lines.
-CH 8: The ActivityEffect – ActivityClass or Activity- NoEffect must equally be represented as horizontal dot- ted lines.
-CH 9: The links between the objects : ActivityClass, ActivityNoeffect, ActivitySelect, ActivityThread, Activi- tySelect/thread, ActivityThread/Select, must be represented as vertical solid lines.
5.1.2. Constraints on the description of entities
- CH 10: All objects are inactive during their descrip- tion.
- CH 11: The order of a differential equation must be greater than or equal to 1.
- CH 12: Algebraic equations are valid if and only if their coefficients are correct.
- CH 13: The fields reserved for the parameters of an object must always contain data.
- CH 14: For every ‘’ActivityConnect’’ and ActivityMo- dul (except ActivityCause), provide a connection point to Ac- tivityCause except for input/output connection points.
- CH 15: All inputs and outputs of an object must be connected.
- CH 16: The terminal object has only one input and no output while the initial object has only one output and no input.
- CH 17: The system must allow the reusability of val- ues entered into the simulation or calculated by it and stored in memory.
- CH 18: Objects should have access to parameters en- tered into the simulation or calculated by it and stored in memory.
- CH 19: The interface for model construction must provide graphical objects in a menu, allowing for their reusability, modification and extensibility.
- CH 20: A logical consequence of CH19 is to provide a minimum configuration of generic objects which can be used to construct all other objects.
5.1.3. Contraints on the simulation
- CH 21: The simulation of a HAD model resulting from the reception of a message from one object to anoth- er can only evolve when the message is validated and its content is true.
- CH 22: The reception of a message causes the simul- taneous activation of immediately following objects and the deactivation of all immediately preceding objects.
- CH 23: Every object has a unique number
-CH 24 : To represent or describe HAD, the following messages are required:
"Displace", "Duplicate", "Delete", "Modify", "Mark", "Search", "Select", «Read parameter ». Consequently, these methods will be declared as "public" in the source code of the simulator.
It is easy to implement the simulator by applying all of these constraints.
The simulator has been modelled using UML 2 [13], to ensure the extensibility and reuseability of its source code. It is implemented in multithread Java [16]. The de- sign details of the simulator will not be presented in this article. The simulator incorporates six (6) different inter- faces, three of which include the model construction inter- face, the model description interface and the simulation interface.
When the simulation is in progress, a dialog box dis-
plays any errors in the model. Such errors may result from the absence of parameter values, inappropriate con- nectivity of objects or some other violation of a constraint. The dialog box also shows the time that has elapsed since the simulation was launched. A red dot moves from the top of the diagram towards the bottom, to show the order in which the objects are activated. This is the sequential phase of the system. By double-clicking on an object, the
IJSER © 2010
10 International Journal of Scientific & Engineering Research, Volume 2, Issue 3,March-
2011
curves representing the continuous-time dynamics of the object are displayed.
Note that the curves represent the operations or me- thods associated with the object. Figure 12 shows the si- mulation interface during the simulation of the liquid- level control system. Figure 13 illustrates the simulation of the HAD model of a system.
The curves are plotted by first resolving equation (1), presented in section 4, to give the result,
f
ISSN 2229-5518
Equation 4 represents the torque of the motor shaft and load.
The different curves obtainable from a SIMHAD simu- lation are presented in [14], [15]. For example, by double- clicking on object number 2 of the diagram in figure 12, the results in figure 13 are obtained.
The speed curves obtained from the simulator are consistent with those found in the literature. The simula- tor also highlights one of the advantages of HAD – encap-
� ( )
(1 -
- r t T - c
![]()
) d
sulation of the actions and interactions of the hybrid sys-
t e J t
r
(3)
tem.
This expresses the speed as a function of time.
The simulator then plots graphs of equations 2 (section 4)
, 3 and 4.
Tr (n) = a.n2 + b.n + c (4)
Details of the functionality and implementation of SIMHAD will be the subject of the next article to be pub- lished by the authors.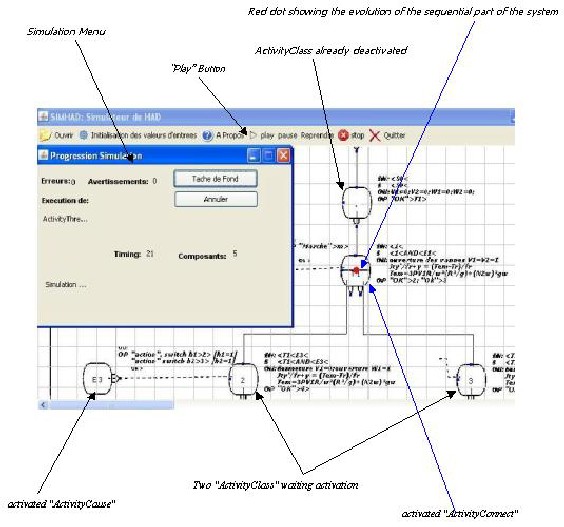
Fig. 12. Simulation Interface showing the liquid-level control system
IJSER © 2010
International Journal of Scientific & Engineering Research, Volume 2, Issue 3, March-2011 11
ISSN 2229-5518
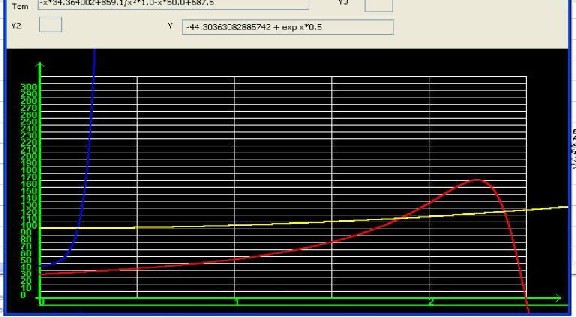
Fig. 13. Curves obtained from SIMHAD
The current phase of our research project, described in this paper, has a triple objective :
- Illustrate the functionality of the HAD metamo- del as a tool which is specifically adapted to the modeling of hybrid dynamic systems such as the liquid-level control system
- Present the bridges which serve as mechanisms for converting HAD models to UML and Grafcet
- Present SIMHAD – a simulator of HAD models
All of these three objectives have been fulfilled.
The next phase of the research project will focus on the extension of SIMHAD. Two aspects merit particular at- tention:
- Integration of the bridges within the simulator, to facilitate the automatic generation of Grafcet and Activity Diagrams from a HAD model
- Solution of nonlinear differential equations, to extend the range of continuous-time models which can be processed by the system.
[1] Tanyi E., Nkenlifack M., “An extended UML for the modeling of hybrid control systems”, in Burnham K.J., Haas O.C.L.(Editors), Proc. of the sixteenth International Conference on Systems Engineering (ICSE2003), Coventry, UK, 9-11 September
2003, Vol.2, pp.681-686, ISBN 0-905949-91.
[2] Tanyi E., Nkenlifack M., “Hybrid Activity Diagrams: Extending
UML for the Modeling of Hybrid Systems”, Poster in
ECOOP’03, 17th European Conference on Object –Oriented Pro- gramming, July 21-25, 2003, Darmstadt University of Technolo- gy, Germany, http://www.st.informatik.tu- darmstadt.de:8080/ecoop/posters/index.phtml - Site Web poster.
[3] [3] M. Nkenlifack, "Modélisation objet et développement d’un atelier de simulation des automatismes industriels hybrides", PhD Thesis, National Advanced School of Engineering (Ecole Nationale Supérieure Polytechnique), University of Yaounde I, Cameroon, 2004.
[4] E. Tanyi, M. Nkenlifack, “An object oriented simulation plat- form for hybrid control systems”, Analysis and Design of hybrid systems (ADHS) 2003, Proc. of the IFAC International Conference, St Malo, France, June 16-18 2003, Edited by S.Engell, H Gue- guen&J.Zaytoon, ISBN 0-08-04044094-0.
[5] T. Noulamo, Modèle Métier et Architectures Génériques pour la Commande et la Surveillance des Systèmes Dynamiques, PhD Thesis, Faculty of Sciences, University of Yaounde 1, Ca- meroon, nov. 2010.
[6] CEI-IEC (International Electrotechnic Commission), Grafcet specification language for sequential function charts, Interna- tional Standard, IEC 60848, 2002.
[7] T. Noulamo, E. Tanyi, M. Nkenlifack, J. Lienou, « Domain Spe- cific Model and Generic Architectures for Control and Monitor- ing of Dynamic Systems », Advances in Computer Science and Engineering Journal, Volume 4, Issue 1, Pages 55 - 75 (February
2010), Pushpa Publishing House, India.
[8] J. Zaytoon, Systèmes Dynamiques Hybrides, Traité Systèmes auto- matisés, Information Commande et Communication, Hermes, Paris,
2001.
[9] O. Bouissou, M. Martel, "Analyse Statique par Interprétation Abstraite de Systèmes Hybrides Discrets-Continus", CEA LIST Laboratoire de Sûreté des Logiciels 22 septembre 2005.
[10] H. Brenier, Métamodèle UML Les spécifications fonctionnelles des automatismes industriels et temps réel, 303–362, Dunod, Paris,
2001.
IJSER © 2010
12 International Journal of Scientific & Engineering Research, Volume 2, Issue 3,March-
2011
[11] M. Flower, UML Distilled, Second edition, Addison-Wesley
Longman, Inc, 2000.
[12] R. David, Alla H., Du Grafcet au Réseaux de Petri, série automa- tique, 2em édition revue et augmentée, édition Hermes 1992,
1997 500 pages (271).
[13] OMG, UML 2.0 Reference Manual, //www.omg.org, 2008.
[14] L. Domche, "Metamodele HAD-Grafcet, Analyse et Mise en Œuvre dans le cadre de la Commande des Réseaux Electriques : cas du Réseau Sud AES SONEL Cameroun", Bachelor Thesis, Electrical Engineering, IUT FV of Bandjoun, University of Dschang, Cameroon, 2009.
[15] F. Fokou, "Metamodele UML–HAD, Analyse et Mise en Œuvre dans le cadre de la Commande des Réseaux Electriques : cas du Réseau Sud AES SONEL Cameroun", Bachelor Thesis, Electrical Engineering, IUT FV of Bandjoun, University of Dschang, Ca- meroon, 2009.
[16] C. Delannoy, Programmer en Java, Eyrolles, France, 2001.
[17] T. Wildi and G. Sybille, Electrotechnique, 3em edition, DeBoeck Uni- versité.
ISSN 2229-5518
IJSER © 2010