
Figure 3.Diagrammatic Illustration of the Proposed Appraoch
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 1
ISSN 2229-5518
Enhancing Bregmanised NLTV Image Denoising using Savitzky Golay filter and SVD
Aswathy Menon, Poornima Rajan, Deepthi.T.V.N, Roshni Das, Sachin Kumar S, K.P.Soman
Centre for Excellence in Computational Engineering and Networking
Amrita Vishwa Vidyapeetham,Coimbatore,TamilNadu,India
Abstract— The existence of noise in digital images hinders the visual effect. To improve the visual quality a well performing denoising technique is a necessity. This paper focuses on image denoising method using Nonlocal Total Variation scheme. Nonlocal Total Variation based denoising technique helps in preserving the edges at the cost of computational load.To reduce the computational load and to speed up the process Split Bregman Optimization technique is employed to the NLTV model. To enhance this denoising Savitzky Golay filter and SVD is incorporated before applying NLTV denoising.The experimental results shows an improvement in the denoising strength which was observed using the standard quality assessment techniques such as SNR, MSE, and PSNR.
Index Terms—Edge Preservation, Image Denoising, Nonlocal Means, Savitzky Golay Filter, Split Bregman Optimization, Singular Value
Decomposition, Total Variation,Image Quality Assessments.
—————————— ——————————
Image denoising is a technique which has been actively re- searched upon since the evolution of image processing. The image noise can be thought of as the variations in the intensity distribution and gets introduced during the image acquiring process due to the electronics involved or while getting transmitted through the channel. Most of the existing image denoising algorithms are based on assumptions on the param- eters used, the type of noise etc and the method compliant for an image may not produce the same result for another sort of an image.
The competent study of an image can be done when there are elevated textures and features. This takes us to the goal of de- noising algorithm that is to conserve image quality by main- taining the edges and features, avoiding over smoothing and to reproduce an ideal image. Many refined denoising tech- niques are available to obtain images of good quality. The pe- riod of 1940’s saw the performance of Weiner filter [1] and followed many successful denoising algorithms which in- cludes the averaging filters, anisotropic filtering, Wavelets, PDE’s, TV regularization [2], [3], [4], [5].
In this paper, 2D gray scale image is preferred for experi- mental purpose. The gray scale image as we know has intensi- ty distribution of 256 levels and lacks colour information. A zero represents black and intensity level 255 represents white. Most of the denoising algorithms use Gaussian noise distribu- tion for the experimental purpose. The denoising algorithm so created can also be eminently used for other noises like Pois- son, Speckle and Salt and Pepper types. This paper uses Ran- dom noise and Gaussian noise distributions.
————————————————
Poornima Rajan is currently pursuing masters degree program in Remote
sensing and wireless sensor networks in Amrita Vishwa vidyapeetham,India.
The recent years saw a rising interest in non-linear filtering technique , the Nonlocal means which was proposed by Bu- ades etal [6] in 2005. The Nonlocal means involves replacing each pixel with a weighted average of other pixels with similar neighbourhoods. Self similarity or redundancies in an image always exist and taking the average of the pixels will result in less noise as specified by Orchand etal [7]. Though it showed a notable result, it was computationally expensive and the edge preservation remained still a striking problem. In 2009, Xavier Bresson [9] combined Nonlocal means with Total Variation Regularization to produce resultant image with enhanced edges and other important texture features. Pixel wise as well as patch based Nonlocal approach is available in which this paper adopts a pixel based approach. The Split Bregman was concatenated along with the proposed technique to increase the SNR value as well as the computational speed and could come forward with worthy results. There has been a lot of ex- periments carried in the arena of Total Variation denoising and the catchiness of the algorithm lies in the fact that the higher intensites were preserved which paved a pathway of competence for wavelet based algorithms.
In this work, a satisfactory Peak Signal to Noise Ratio (PSNR) value is achieved by incorporating Savitzky Golay filter before denoising and Singular Value Decomposition (SVD) image reconstruction using limited number of components after im- age denoising. We have assessed the approach using the three quality estimation techniques Signal to Noise Ratio (SNR), Mean Square Error (MSE) and PSNR. Savitzky Golay is a par- ticular type of polynomial based low pass filter which is well adapted for smoothing and helps in preserving higher intensi- ty values. Despite the fact that significant results are pro- duced, Savitzky Golay filtering approach has not yet been broadly pondered upon in signal filtering area. Denoising techniques requires definite measurements to be done on the denoised image to comprehend the competence of the ap- proach being raised, for which the fine inferences can be done
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 2
ISSN 2229-5518
by comparing it with the original image. PSNR should be high for the resultant image indicating that the algorithm is re- markable enough to be put forth as an excellent contribution towards quality improvement of images.
The further sections of the paper are organized as follows: Section 2 gives an insight into the Savitzky Golay filter. Sec- tion 3 deals with the proposed approach followed by sub sec- tions which enlighten upon the Nonlocal means, Total Varia- tion, Split Bregman and Singular Value Decomposition. The paper concludes with the results and discussions in section 4 and the conclusion in section 5.
The idea of the Savitzky Golay (SG) filtering technique was introduced in 1964 and gained notice with its ability to main- tain sharp features in the image. The alternate filtering tech- niques like the moving average failed in preserving the edge features. Along with smoothing out the data, it proved suc- cessful in maintaining the minima and maxima effectively by utilizing the least squares technique [10]. The idea of SG filter was to find the filter coefficients that preserve higher moments or features in an image. In here, each point is a least square fit which is not a constant but a polynomial that is quadratic and is done by using a moving window assuming that the data points are equally spaced to eliminate the computational diffi- culty. Though equivalent to a smoothing operation least squares polynomial fit is efficiently performed in a one step procedure [11].
The mathematical form of the least squares fit can be ex- plained as follows [11]:
n R
and SVD image reconstruction is applied to increase the algo- rithmic strength to obtain an image with edge features and a higher PSNR rate. The Savitzky Golay filter is used to smooth out the noises present in the image with a higher degree of edge maintenance. Followed by NLTV bregmanised denoising and the prominent factor is the SVD reconstruction of image.
Figure 3.Diagrammatic Illustration of the Proposed Appraoch
3.1 NONLOCAL MEANS
The Nonlocal means algorithm was first formulated in 2005 by Buades etal and has found immense applications in wider area of research covering medical images to satellite images. It is a generalisation of the Neighbourhood filter originally devel- oped by Yaroslavsky in 1985. The pixel or patches that we consider may not be nearer to the pixel under consideration.
g i
n n L
c n f i n
(1)
That is, any point can directly interact with any other point in the image domain and hence the name Nonlocal. The de- noising of images can be done efficiently with the help of Non-
Here
gi is the estimated signal value and
f i n is the input
local means algorithm which uses the redundancy present in
the image. By redundancy it means the pixels having the simi-
signal. If the pixel at i is taken into consideration then nL is
lar intensity characteristics.
the number of data points towards the left and nR
is the
number of data points towards its right and constant![]()
c 1
n nL nR 1
The SG filter tries to find out these filter coefficients for which the higher intensity values are preserved. The window is
The Nonlocal means is a kind of an averaging filter in the
sense that it uses the weighted average of the neighbourhood
pixels and replaces the pixel value under consideration [8].
The efficiency of Nonlocal means lies in preserving the fea-
tures by not causing blur or lose of edges in the denoised im-
age. But the shortcoming of Nonlocal means lies in its compu-
moved from
fi nL to
f i n R
and least squares fit are per-
tational complexity. The approach does not make any assump-
formed to replace each pixel value. The SG filters are most
tions of the image other than considering that it has a lot of
self similarity. Self similarity refers to those pixels with similar
useful for larger values of nL
and nR
where only small
neighbourhood.
amount of smoothing will be done. The obtained resultant image is used for further processing. That is the smoothed out image with enhanced edge is applied to the Nonlocal TV algo- rithm.
The observation model can be depicted as
v(i) x(i) n(i)
( 2)
The work explicitly focuses on the Nonlocal Total Variation with Split Bregman method to which a smoothing approach
Where x of image size N M is corrupted by additive white Gaussian noise or Random noise n and v is the noisy image. The Nonlocal means filtered image model can be represented by the equation given below which the standard framework is
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 3
ISSN 2229-5518
proposed by Buades etal,
w ( x. y ) u ( y ) d y
N L v ( x )
(3)
preserve the edge details and recreating an estimate of the original image iteratively, it does a minimization approach of the total variance. The benefit of the combination of the two
w ( x. y ) d y
techniques appears to be that the method manages to capture
the best features, the patch redundancy in NL means and the
Here,
u0 ( y)
is the noisy image. NLv(x) computes the Non-
nice denoising of edges in TV [14].
local means of the noisy image. Whereas w(x, y) is the weights
assigned based on the similarity between patches located at x
and y. The similarity measure is decided based on the Euclide-
an distance function.
The weights can be defined as,
The classical TV minimization was proposed by Rudin etal [15] which is minimization of energy functional. Gilboa and Osher proposed a Nonlocal TV method as depicted below,
w( x, y) exp
Ga ( z) ![]() u0 ( x z) u0 ( y z)
u0 ( x z) u0 ( y z)![]()
2 dz
(4)
inf F (u)
u
![]() NL u
NL u ![]()
![]()
u u0 dx
2
(6)
h2
In which the Nonlocal gradient operator is replaced as fol-
lows,
The value
2
Ga ( z) ![]() u0 ( x z) u0 ( y z)
u0 ( x z) u0 ( y z)![]() dz
dz
is the dis-
2
2
tance function which plays a role in deciding the weight be-
u( y) u( x)
w( x, y)dy
2
![]()
u u0 dx
(7)
tween the patches at locations x and y.![]()
Ga is the Gaussian
Where, u0 is the noisy image and the parameter λ is the regu-
function with standard deviation a. The weight parameter
ranges between zero and is positive and symmetric. Whereas, the constant h, is the weight decay control parameter or de- gree of filtering. The parameter plays a crucial role in de- noising the image. It controls the degree of decaying of expo- nential function and hence the degree of decaying of the weight as a function of the Euclidean distance. If the parame- ter h is set too low then noise removal will be poor and if set too high the denoised image will become blurred. The size of the searching window we consider is a crucial parameter in Nonlocal means denoising approach.
For discrete points i and j for x and y belonging to equation
4 can be formulated as
j wij u j
larization factor. The regularization parameter needs to be
carefully chosen. The first term is the regularization term
which helps in smoothing of the image noise and the second
term is the data fidelity term which helps in obtaining the
original image. The iterative process of NLTV can be opti-
mized using the convex unconstrained optimization technique
which is the Split Bregman iterative procedure.
A well posed optimization procedure was proposed by Tim Goldstein and Stanley Osher [16] which can be incorporated very well with TV based methods. The mathematical deriva- tion is based on the paper by Xavier Bresson. The fundamental idea of the Split Bregman Optimization is introducing an aux-
iliary variable in to the NLTV functional and the equation
ui
j wij
(5)
changes to the form depicted by Xavier Bresson as follows,
Where ui
is the denoised image, w is the weight parameter. 2
The window size for the work is considered as 11 11 and
was not made adaptive. Similarly, all the other parameters
were also kept constant which include the parameter h and the
inf
u ,d
![]()
![]()
d ![]() (u u0 ) ,
(u u0 ) ,
2
such that NLu d
(8)
weight.
The Nonlocal means was adapted along with the variational architecture and it was widely studied by Gilboa and Osher,
Here, d is the auxiliary variable introduced to make the pro-
cess computationally efficient. The equation is now a con-
strained minimization problem. To make it an unconstrained
minimization problem, the Split Bregman iteration is to be
formulated as,
Zhou and Scholkopf [12], [13] and other eminent scholars. The
inf F(u) arg min
![]()
d (u u )2 d
![]()
u bk dx
(9)
Nonlocal Total Variational framework algorithmic view makes it altogether a non linear approach. The Total Variation based techniques is broadly used in inverse problems like denoising, inpainting etc which gives out excellent results.
The main principle behind Total Variation denoising is the signals with spurious details will have high total variance and hence the gradient of the image will also be high. In a way to![]()
u u,d 2 0 2 NL
The auxiliary variable b accelerates the iteration. The above mentioned equation (9) uses two sub problems one for u and the other for the auxiliary variable which is the bregman dis- tance function d. The minimization of u can be attained using Gauss Seidal iterative scheme and the minimization of d by a
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 4
ISSN 2229-5518
soft thresholding formula.
The two sub problems is classified as follows,
minimization of u k+1
k k
(10)
‘∑ ‘have singular values i in decreasing order. That is, with increasing rank the singular values decreases considerably. The first singular values have high intensities and the intensity level decreases as the order increases. An interpretation of it
may be viewed as the image information content will be high
(u u0 ) divN L ( d
minimization of d,
N L u b
) 0
and for the last components it will be less. The SVD image reconstruction process can be explained as follows:-![]()
u k 1 bk
![]()
(11)
A U V T
d k 1 N L max(
u k 1 bk
, 0)
NL
![]()
![]()
u k 1 bk NL
Here, the variable k represents the present iteration and k+1 the next iterative level. After the minimization the Bregman variable b is updated as
k 1
ij
b k
wij
k 1
j
u k 1
k 1
ij
(12)![]()
The splitting of the minimization problem into two sub prob- lems makes it easy to optimize and hence the complexity in performing the computations is drastically reduced. The two images, at present iteration and at the previous iteration will be compared and iteration ends when the specified tolerance rate is reached.
The algorithmic outline can be depicted as follows:
I n iti a l iz e : u 0 u , d 0 , b 0
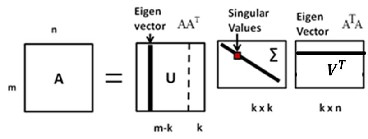
Figure .3.4.1. Illustration of SVD Decomposition
If there are k singular values then using only r values (r<n), we can reconstruct the image by preserving the required edge and texture image details. That is the reconstruction equation is as follows,
r
![]()
w h il e u k 1 u k
![]()
to le ra n c e
A
i 1
i u i v i
(13)
e n d
s o l v e th e s u b p r o b le m o f u s o l v e th e s u b p r o b le m o f d
u p d a te B r e g m a n v a r ia b le b
Here r singular values are used for the image reconstruction. By means of employing the SVD image reconstruction, we obtained an increase in the PSNR value which shows that the artifacts in the image are reduced to a certain extent. The ex- perimental result is compared by taking various components range and the plots shows that there is slight change in the
Singular Value Decomposition has been a significant area un- der discussion in linear algebra since its development and its finest capabilities found feasibility in digital image processing too. The transparency of the technique lies in the fact that with
smaller set of values the original image can be reconstructed
by preserving the most important features and textures in the
image. The fundamental concept of SVD is transformation of
the matrix in to three matrices. The digital image is also con-
sidered to be in the form of matrix, and henceforth an image
can be reformed into the three matrices [17].
MSE and PSNR values which is clearly attributed in the results and discussions section of the paper.
4 QUALITY ESTIMATION TECHNIQUES
The performance of the denoising method can be quantitative- ly analysed using the quality metric peak signal to noise ratio and the unit of measurement is in decibels. Gaussian noise model is considered for most of the denoising algorithms and the variance of various values is added to the test image to study the performance of the proposed algorithm. The PSNR is defined as below,
In this work, the image after denoising which is in the form of a matrix, applying SVD on it, transforms in producing two
P S N R ( u 0 , u ) 1 0 lo g 1 0
2 5 5 2
![]()
M S E ( u 0
, u )
(14)
orthonormal matrices and a matrix with singular values in the diagonal. The decomposition is pictorially shown in figure
3.4.1. In that figure matrix A with m rows and n columns is decomposed into two orthonomal matrices U and V. The SVD transformation can be computed as A UV T . The matrix
Where, MSE (u0 , u) ,is the difference between the original
image and the denoised image given by the equation,
s u m ( u u ) 2
M S E 0 , where m n is the size of the image.
m n
5 RESULTS AND DISCUSSION
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 5
ISSN 2229-5518
The basic idea behind the projected realization was to incorpo- rate SVD with a filtering approach. The study showed a result with good PSNR which highlights the usability of SVD image
reconstruction approach of images. The denoising results are presented in Fig 5.1
Input Image Noisy Image


(a) (b)
 Split Bregman
Split Bregman
(c) (d)
NLTV SVD


(e) (f)
Figure 5.1.(a), (b-Random Noise), (c), (d), (e), (f) Denoising results for Barbara Image
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 6
ISSN 2229-5518
SNR PLOT
20
PSNR PLOT
40
18 35
16
30
14
12 25
10 20
8 15
6
10
4
2 5
0 0
(a) (b)
100
MSE PLOT
SNR PLOT
20
18
90
16
14
80
12
70 10
8
60
6
4
50
2
40
0 50 100 150 200 250
Singular values
0
0 50 100 150 200 250
Singular values
(c) (d)
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 7
ISSN 2229-5518
100
MSE PLOT
PSNR PLOT
40
35
90
30
80
25
70 20
15
60
10
50
5
40 0
(e) (f)
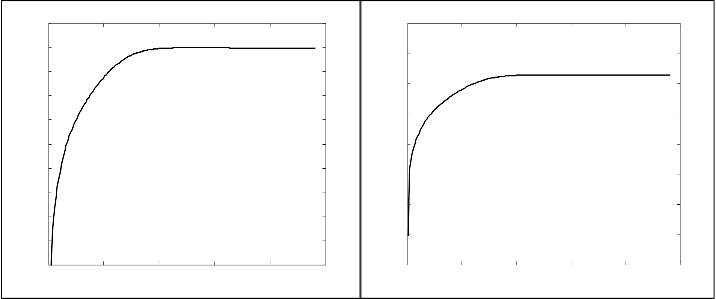
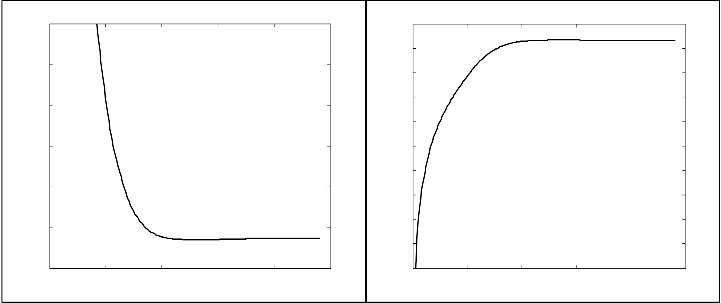
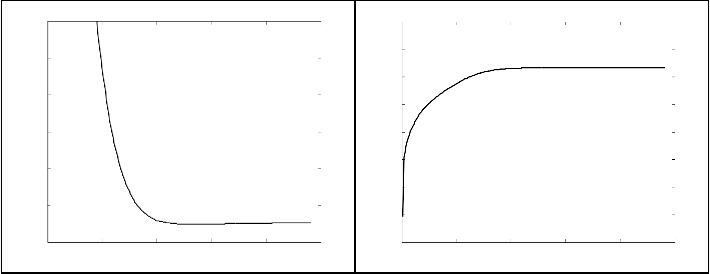
Figure 5.2. Plots shows the results for SNR, MSE, PSNR for Gaussian (a), (b), (c) and Random Noise (d), (e), (f) experiments
The SNR, MSE and PSNR values were calculated using the standard formulas using MATLAB and the ouputs were plot- ted. For Gaussian noise a maximum PSNR of 32.042 dB was obtained whereas for Random noise a maximum PSNR of
30.83 dB was gained.
The experiment was conducted using Gaussian noise as well
as Random noise and is done in MATLAB version environ-
ment. The Gaussian noise with mean zero and a variance of
.001 were considered for the test. The test was performed on
Barbara image with a size of 247 by 266 pixels in it. The edge
features were preserved successfully in the denoised image.
It can inferred from the Figure 5.2. (a), (c), (d), (f) that the SNR and PSNR value is maximum at a point when the singular values is between 100 to 150. The value of PSNR and SNR is minimum when only one singular value is considered. As the singular value components increases, the number of infor- mation content gradually increases, which can be observed from the quality metrics measured. An observation made from the obtained graph figure 5.2 is that there is a slight decrease in the SNR and PSNR value for higher amount of singular components. This indicates that there is a possibility of noise components at lower intensity values which do not contribute any information to the image reconstruction. Similar observa- tions can be made for the random noise experiments as well.
In this paper, our work addresses the fundamental prepro- cessing step image denoising. We have proposed a denoising technique which uses the Savitzky Golay filter before perform- ing the NLTV denoising with Split Bregman Optimization to preserve the higher intensities. SVD image reconstruction en- hances the NLTV denoised image. The salient feature of the overall method includes:(1) smoothing is done as a default
processing by SG filter, (2) NLTV denoising helps in preserv- ing the edge information, (3) Split Bregman Optimization in reducing the computational complexity and speeds up the process, (4) SVD image reconstruction which improves the PSNR value of the denoised image. The experiment is carried on the Barbara image and the proposed method works rea- sonably well with Gaussian and Random noise models.
As a future work the weighting parameter used in the pro- posed denoising method can be made adaptive which might further improve the denoising results.
[1] J.S.Lee, ”Digital Image Enhancement and Noise Filtering by Use of Local Statistics”, IEEE Transactions on Pattern Analysis and Machine Intelliigence, Vol.2, no.2, pp.165-168, 1980
[2] J.Weickert, ”Anisotropic Diffusion in Image Processing”, 1998
[3] D.Donoho, ”Denoising by Soft-Thresholding”, IEEE Transactions on Information
Theory, Vol.41, no.3, pp.1613-627, 1995
[4] P.Perona and J.Malik, ”Scale Space and Edge Detection Using Anisotropic Diffu- sion”, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.12, no.7, pp.629-639, 1990
[5] Sarita Dangeti, “Denoising Techniques - A Comparison”, B.E., Andhra University College of Engineering, Visakhapatnam, India, pp. 5-10, May 2003
[6] A.Buades,B.Coll and Jean-Michel Morel, “A Nonlocal Algorithm For Image Denoising”, proc..int .Conf.Computer Vision And Pattern Recognation., Vol.2, 2005, pp.60-65
[7] J.Orchard, M.Enrahimi, A.Wong, ”Efficient Nonlocal Means Denoising
Using The SVD”, IEEE Conference For Image Processing , 2008
[8] A.Buades, B.Coll and Jean-Michel Morel., ”A Review Of Image De- noising Algorithms, With A New One”, Multisacle Model.Simul., Vol. 4, No.2, pp. 490-530, 2005
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 8
ISSN 2229-5518
[9] Xavier Bresson, “A Short Note for Nonlocal TV Minimization,” June 25, 2009
[10] A.Savitzky and M.J.E.Golay, ”Smoothing And differentiation Of Data By Simplified Least Square Procedures”, Analytical Chemistry, Vol.36, no.8, July 1964
[11] Chapter 14, Statistical Description of Data, “Savitzky Golay Smoothing Filters”, Numerical Recipes of C-The Art of Scientific Computing , pp.650-655, 1988
[12] G.Gilboa and S.Osher, ”Non Local Linear Image Regularization And Supervised Segmentation”, SIAM Multisale Modeling And Simula- tion(MMS), Vol.6, No.2 , pp.596-630, 2007
[13] D.Zhou and B.Scholkopf, “A Regularization Framework For Learning From Graph Data” , Workshop on Statistical Relational Learning At International Conference On Machine Learning,Banff, Canada, 2004
[14] C.Louchet and L.Moisan, ”Total Variation As A Local Filter”, SIAM J,
Imaging Sciences, Vol.4, no,2, pp.651-694, June 21, 2011
[15] L.Rudin, S.Osher and E.Fatemi, ”Non Linear Total Variation Based Noise Removal Algorithms”, PhysicaD, Vol.30, no.1-4, pp.259-268, No- vember, 1992
[16] T.Goldstein and S.Osher, "The Split bregman Method For L1 Regularized
Problems”, SIAM J.Imag.Sci.vol.2, no. 2, pp.323-343, May 2009
[17] L.Cao, "Singular Value Decomposition Applied To Digital Image Pro- cessing”
IJSER © 2013 http://www.ijser.org