International Journal of Scientific & Engineering Research, Volume 4, Issue Ş, 2013
ISSN 2229-5518
Enhancement of Ultrasound Images Using
RADWT
Paras Bhatia, Rashmi Kumari
Abstract— Feature preserved enhancements are necessary in medical ultrasound images. The quality and important information present in ultrasound images are affected by speckle which makes the post processing difficult. A technique based on rational dilatio n wavelet transform (RADWT) is applied on medical images to enhance the quality of speckle noise affected images. A new family of wavel et transform is presented for which the frequency resolution can be varied to provide the effectiveness of noisy coefficients. Denoising efficiency is improved by applying bilateral filter and different threshold schemes to noisy RADWT coefficient and edge features are preserved effectively, blurring associated with speckle noise is less and important details are enhanced properly for better visual illustration of ultrasound images. This approach helps us to improve the quality of the ultrasound images. Experimental results are shown for noise suppression, feature and edge preservation in different measures.
Index Terms— Bilateral Filter, Image Enhancement, Rational Dilation, Speckle Noise, Thresholding, Ultrasound Images, Wavelet
Transform.
197
—————————— ——————————
Ow a days, Image enhancement is a necessary need in medical images, in medical images ultrasound are wide- ly used among others, because of its cost, effectiveness
portability and safety [1].Ultrasound obtained are of very poor quality which makes the processing complex and difficult. Images obtained from coherent energy source suffer from backscattered echos generated from randomly distributed scatters called speckle [2].
Speckle is a multiplicative noise which has undesirable inter-
ference effect on the images which makes the diagnosis diffi-
cult. Reduction of these speckle are necessary to improve the
quality of ultrasound image. Sometimes most important data
is suppressed while processing the reduction of speckle. So,
the algorithm should be designed in such a manner that signif- icant information should not lose or suppressed and smooth
image should obtain.
Ultrasound reduction method can be classified by two
methods: - image averaging and image filtering.
Image averaging [3] is usually achieved by averaging a se-
ries of uncorrelated ultrasound images in the spatial or fre- quency domain. We could use filtering method as an alterna-
tive for clinical purpose which can be further classified as spa- tial filtering such as non-linear, linear etc. Linear spatial [4] introduces severe blurring and loss of data which is based on pixel replication many non linear filter have been introduced such as median and weighted median filter (AWMF) to elimi- nate the requirement in median filtering [5]. The various filters used in spatial domain are as proximity based [6], filters Order statistic filter [7] and Wiener filter [8]. Weiner filter works bet-
————————————————
ter when the noise is of constant power additive noise while proximity filters help in removing the noise at the cost of blur- ring the edges.
Efforts have been made to reduce the speckle noise and overcome the drawback of spatial domain filtering using wavelet transform. Denoising method [9] in soft thresholding method is presented in which main critical task of threshold- ing is the selection of the trhreshold value [10]. Earlier in de- noising of images Baysian approach was used but now a day, the research is concentrated on wavelet based method, which can be optimised for different wavelet coefficients [11] by us- ing different noise models [12]. Total variation filtering meth- od based on wavelet [13] is also proposed in which several iterations are taken from noisy images for suppressing the gaussian noise the exceedings numbers of iterations, exceeds to blurring effect. Wavelet thresholding was proposed as an alternative method [14] to the bilateral filter, which is a non linear filter and is used in spatial domain for edge preserved denoising. It provides effective denoising [15] and is better in sense of edge preserved denoising. This method is proposed to keep the potential feature of both bilateral filter and wavelet thresholding simultaneously.
Wavelet domain has basic properties like decomposition of wavelet coefficients and sparsity, because of these properties researchers are more focused on this wavelet domain [16]. Sparsity property of the wavelet transform and the capacity for analyzing the time frequency information are combined together with the different frequency subbands, making the wavelet area ideal. Whereas, the wavelet transform is an effec- tive tool but it has a poor frequency resolution and low Q- factor for smoothing the signal. A non linear filter depending on the combination of wavelet transform and rational dilation is used to enhance the ultrasound images [17]. The combina- tion of bilateral filter and rational dilation wavelet transform is applied over the various test images to enhance the quality of corrupted and noisy medical image and its analysis is present- ed in this paper.
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue Şǰȱ ȱŘŖŗř

ISSN 2229-5518
198
a P b
b P* a
Q s s Q*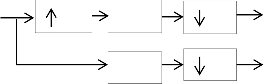
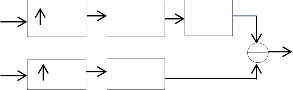
Fig.1 Analysis and Synthesis filter bank
xi
![]()
C j N i D f i, j x j
(4)
RADWT is a discrete wavelet transform with the wavelet vari- ables of frequency and time subbands as a scale and position along with the rational-dilation factor. Different wavelet trans- form are used in applications of image processing such as
Where i and j are coordinate vectors,
�𝑓(�, �) is representing the domain filter and 𝑅𝑓(�, �) is repre-
senting range filter as components of bilateral filter, which are
defined as:
sharpening, denoising, debluring etc. those application are
inveritible for which the transform are required. In RADWT,
Df (i, j) exp ||
j i || 2
(5)
flexibility is provided by increasing the resolution from one resolution to another resolution level because of the low Q- factor [18] the dyadic wavelet transform limits the effective-![]()
2 2
|| x( j) x(i) || 2
![]()
Rf (i, j) exp
ness of RADWT.
The RADWT is implemented by using two iterated channel
2 2
(6)
filter bank as shown in Fig. 1 with rational dilation factor (a and b), and a high pass sampling factor (s). the RADWT is charterised by its redundancy i.e. oversampling rate [19].
P is a low pass filter and Q is a high pass filter in the analysis filter bank. If RADWT has a perfect reconstruction property then it is self inverting. The condition of the filter P and Q to get the perfect reconstruction are explained as follows:
N (i) is the spatial neighbourhood of x,
C is the normalization constant defined as below
� = ∑ � 𝜖𝑁(�)�𝑓(�, �)𝑅𝑓(�, �) (7) Where 𝜎 𝑎𝑛𝑑 𝜎 are the domains and range parameters which
control the behaviour of the weights [20]. The bilateral filter
will act as a smoothing filter and will blur the image if param- eters values are set too high. If the values are too low, noise
P 0
Q 0
![]()
![]()
![]()
![]()
for ,
b
![]()
![]()
![]()
![]()
![]()
for 0, 1
s
![]()
2
(1)
(2)
cannot be removed.
In thresholding the energy of a signal is focused on few coeffi- cients and the energy of noise is spread coefficients in RADWT domain [21]. Denoising can be achieved by applying thresh- olding function to the coefficients. The important key feature![]()
![]()
1 p
![]()
![]()
1 Q 2 1
for 0,
(3)
of the original image are preserved, when the transformed
ab a s
The length of the signal should be multiple of b and s for the perfect reconstruction of the wavelet transform. Inverse ra- tional-dilation wavelet transform (IRDAWT) is computed by transform of RADWT. By choosing parameters a, b and s high- Q factor can be achieved.
Bilateral Filter (BLF) is a type of non linear filter for denoising with in the spatial domain, while preserving the edge infor- mation. The pixel values are obtained by a weighted sum of
coefficient are compared against threshold to remove the noise
from image. There are two types of thresholding as given be-
low:
If the coefficients having value less than the particular thresh- old are set to zero and the non zero coefficients are scaled, the thresholding scheme are called the soft thresholding. It is used to approximate the noisy coefficients of the signal.
So the soft thresholding [22] is computed as follows:
pixel in a neighborhood in bilateral filtering method and the
d i, j T ;
d i, j T
weight depends on the the spatial distance of the pixel around
THRd i, j
i, j T ;
d i, j T
(8)
the local neighborhood of a pixel. The combination of domain
filter and range filter is required to achieve it. The output of
BLF for a pixel located at i is :
0;
![]()
![]()
d i, j T
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue Şǰȱ ȱŘŖŗř
ISSN 2229-5518
199
Noisy x
𝐶𝑁
�𝑁
Bilateral Filter
𝑟�𝑁
𝑟�𝑛
𝑥̂
Image RADWT
(N level) �
�
Thresholding
𝑟�
IRADWT
(N level)
Restored
Image
Fig.2 Block Diagram
The coefficient whose absolute values are lower than the threshold (T) set to the value zero and the other values are left the same is done in hard thresholding [23]. The noise free coef-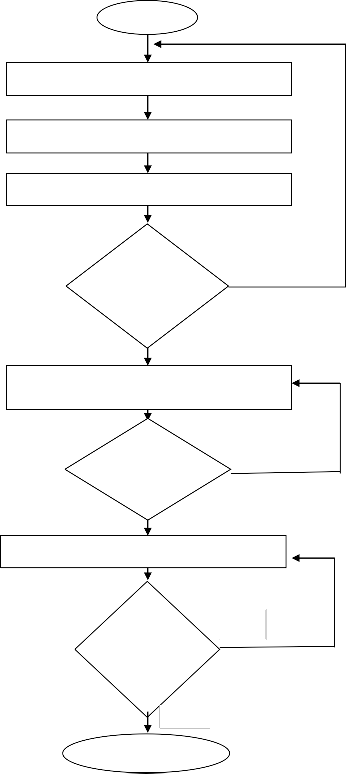
Start
ficients are estimated as follows.
Select the number of decomposition level
i, j ;
![]()
![]()
d i, j T
THR d i, j
d
0;
otherwise
(9)
Select the dilation factor (a and b)
T N
![]()
2 logN
Where N is the Length of the signal and N is the estimated standard deviation of noise.
Three basic steps are involved in denoising process as shown in Fig 2
1. For computation, the RADWT noisy coefficient, select the number of decomposition level, dilation factor (a and b) and high pass sampling factor
2. To obtain the modified RADWT coefficient, select and perform filtering algorithm on these noisy coefficient.
3. By using inverse RADWT, reconstructed image is ob- tained.
Apply RADWT (𝑊 ) on noisy input image signal 𝑥(�, �) at
different level. Decomposed set of RADWT coefficients as a
vector of 𝜁 consisting of N subbands with different spectral
resolution such as
Select high pass sampling factor (s)
If RADWT No
coefficient
is obtained
Yes
Select the filtering algorithm on noisy coefficient
𝑊 𝑥(�, �) = 𝜁(�, �) (10) Where 𝜁 = (𝑑 , 𝑑 , 𝑑 … . . 𝑑 , � )
Lower stage coefficient coefficients (𝑑 ) contain high frequen-
cy noise element.and in the last stage coefficient (� ) noise is
approximately negligible. Noise is suppressed in each layer
after perfoming the appropriate filtering.
If modfied RADWT is obtained
No
Yes
Finally, bilateral filter (BLF) is applied on RADWT coefficient
i.e. low frequency component(� ) and rest of all RADWT coef- ficient i.e.𝜒 is threshold by appropriate thresholding tech-
nique (THR)
Use inverse RADWT (IRADWT)
rCN
BLF CN and r N
THR N
(11)
Where 𝑟𝜒 = [𝑟𝑑 , 𝑟𝑑 , 𝑟𝑑 … . . 𝑟𝑑 ]
To get the reconstructed signal, IRADWT (𝑊 ) is applied
on the filtered coefficients which is the approximation of the
noisy image signal 𝑥̂(�, �)
If recon- No
structed
image is
obtained
IJSER © 2013
http://www.ijser.org
Stop
Yes
International Journal of Scientific & Engineering Research Volume 4, Issue Şǰȱ ȱŘŖŗř
ISSN 2229-5518
There are several parameters on which the performance of this method depends such as dilation factor (a and b), decom-
position level (J) and high pass sampling factor (s), 𝜎
and 𝜎 .The optimal value of parameters used for this method
are a=3, b=4, s=2, J=4, for RADWT, window size 11x11,
𝜎 = 1.8 and 𝜎 = 2𝜎 .
The performance of the model is tested over various test
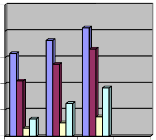
images. The PSNR, MSE and Threshold values are calculated for the test images (Liver, Kidney, Pancreas and Gall Bladder)
are shown in table 1 and table 2 for qunatitaive comparisons and Graph1 and Graph 2 is showing its pictorial presentation.
200
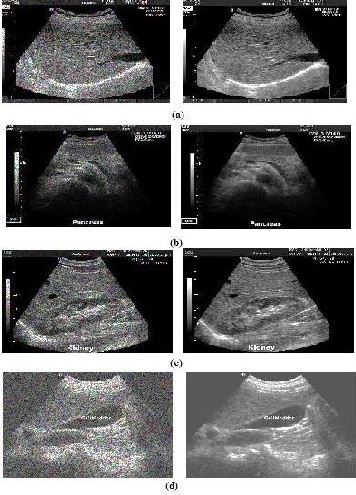
Fig 3. Visual illustration of ultrasound images with speckle noise and enhanced image (a) Liver (b) Pancreas (c) Kidney
(d) Gall Bladder
Table 1 Values of MSE and PSNR on different test images.
Test Image | Threshold (T1) | Threshold (T2) | Threshold (T3) |
Liver | 0.1579 | 0.1828 | 0.2067 |
Kidney | 0.1057 | 0.1374 | 0.1665 |
Pancreas | 0.0155 | 0.0255 | 0.0371 |
Gall Bladder | 0.0329 | 0.0625 | 0.0923 |
Table 2 Vlaues of Threshold T1, T2, and T3 on different test values
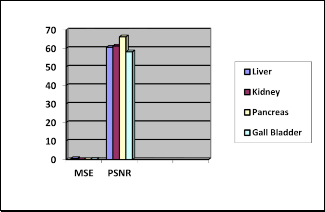
Graph.1 Comparative values of MSE and PSNR
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue Şǰȱ ȱŘŖŗř
ISSN 2229-5518
201
0.25
0.2
0.15
0.1
0.05
0
Threshold
(T1)
Threshold
(T3)

Liver Kidney Pancreas Gall Bladder
[10] D. L. Donoho and I. M. Johnstone, (1995) "Adapting to unknown smoothness via wavelet shrinkage," Journal of the American Statisti- cal Association, vol. 90, no. 432, pp. 1200-1224.
[11] G. G. Bhutada, R. S. Anand, and S. C. Saxena, (2010) "Fast adaptive learning algorithm for sub-band adaptive thresholding function in image denoising," International Journal of Computational Intelli- gence Studies , vol. 1, no. 3, pp. 227-241,
[12] G G. G. Bhutada, R. S. Anand, and S. C. Saxena, "Fast adaptive learn- ing algorithm for sub-band adaptive thresholding function in image denoising," International Journal of Computational Intelligence Studies , vol. 1, no. 3, pp. 227-241, 2010
[13] B. A. Abrahim and Y. Kadah, (2011) "Speckle noise reduction method combining total variation and wavelet shrinkage for clinical ultra-
Graph.2 Comparative values of Threshold T1, T2, T3
A non-linear filtering scheme based on RADWT has been im- plemented on the various standard medical images. In this method the frequency resolution variation feature of the RADWT is used to decompose the noisy image into different subbands at different levels. BLF reduces the high amplitude noise components and thresholding upgrades the denoising efficiency. The results have shown in visual context as well as quantitative parameters in terms of PSNR and MSE.
I would like to thank my parents for believing in me and I would like to thanks my guide without her guidence I would not be able to become what I am.
[1] A.P. Dhawan,(2003): „Medical Image analysis‟, John Wiley and Sons
Inc.
[2] C.B. Burckhardt (1978): „Speckle in ultrasound B-mode scans‟, IEEE
Transaction on Sonics and Ultrasonics, vol.SU-25, pp, 1-6.
[3] J.G. Abbott and F.L. Thurstone (1979): „Acoustic speckle: Theory and experiment analysis,‟ Ultrasonic Imaging, Vol.1, no.4, pp.303-324.
[4] W.K. Pratt (2006): „Digital Image Processing, John Wiley and Sons‟.
[5] T.Loupas,(1989): „ An adaptive weighted median filter for speckle suppression in medical ultrasonic images, IEEE Transactions on Cir- cuits and Systems, vol. 36, no.1,pp.129-135.
[6] Tao Chen and Hong Ren Wu, (2001). "Adaptive impulse detection using center-weighted median filters," IEEE Signal Processing Let- ters, vol. 8, no. 1, pp. 1-3
[7] S. Marshall, (2004) "New direct design method for weighted order statistic filters," IEE Proc.-Vision, Image and Signal Processing, vol.
151, no. 1, pp. 1-8.
[8] R.C. Gonzalez and R.E. Woods (2001), „Digital image processing.
Prentice-Hall
[9] D. L. Donoho and I. M. Johnstone, (1994) "Ideal spatial adaptation by wavelet shrinkage," Biometrika, vol. 81, no. 3, pp. 425-455.
sound imaging," Proc. 1st Middle East Conference on Biomedical En- gineering (MECBME), pp. 80-83. .
[14] C. Tomasi and R. Manduchi , "Bilateral filtering for gray and color
images," Proc. Sixth International Conference on Computer Vision , 1998, pp. 839-846
[15] R. Vanithamani and G. Umamaheswari, (2011) "Wavelet based des- peckling of medical ultrasound images with bilateral filter," Proc. IEEE Region 10 Conference TENCON, , pp. 389-393
[16] I. Bayram and I. W. Selesnick, "Frequency-domain design of overcomplete
rational-dilation wavelet transforms," IEEE Transactions on Signal Pro- cessing, vol. 57, no. 8, pp. 2957-2972, 2009.
[17] Deep Gupta, R.S Anand and Barjeev Tyagi (2012) “Enhancement of medical ultra sound images using non-linear filtering based on ra- tional-dilation wavelet transform”, Proceedings of the World Con- gress on Engineering and Computer Sciences Vol I.
[18] M. Zhang and B. K. Gunturk, (2008) "Multiresolution bilateral filter- ing for image denoising," IEEE Transaction on Image Processing, vol.
17, no. 12, pp. 2324-2332.
[19] I. Bayram and I. W. Selesnick, (2009.) "Frequency-domain design of over complete rational-dilation wavelet transforms," IEEE Transac- tions on Signal Processing, vol. 57, no. 8, pp. 957-2972.
[20] M. Zhang and B. K. Gunturk, "Multiresolution bilateral filtering for image
denoising," IEEE Transaction on Image Processing, vol. 17, no. 12, pp.
2324-2332, 2008.
[21] C. S. Anand and J. S. Sahambi, "Wavelet domain non-linear filtering for MRI denoising," Magnetic Resonance Imaging, vol. 28, no. 6, pp.
842-861, 2010.
[22] D.L. Donoho, "De-noising by soft thresholding," IEEE Transaction on
Information Theory, vol. 41, no. 3, pp. 613-627, 1995
[23] Savita Gupta, R.C. Chauhan, and S.C. Saxena, "Wavelet based statistical approach for speckle reduction in medical ultrasound images," Medical & Biological Engineering & Computing, vol. 42, pp. 189-192, 2004
IJSER © 2013