International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 1

ISSN 2229-5518

Dynamic Behavior of Underwater Towed-cable in

Linear Profile

Vineet Kumar Srivastava, YVSS Sanyasiraju, Mohammad Tamsir

Abstract— In this paper, a numerical approach is presented which is capable of predicting dynamic behavior of underwater towed- cable structures when tow-ship changes its speed in a fixed direction making linear profile. A three-dimensional model of underwater towed system is studied. The governing equations for the system are solved by using a central finite-difference method. The solution of the finite-difference form of the assembled of non-linear algebraic equations is obtained by Newton’s method. Since the underwater towed cable model uses implicit time integration, it is stable for large time steps and is an effective algorithm for simulation of large- scale underwater towed systems. The solution of this problem is of practical importance in the estimation of dynamic loading and motion, and thus has direct application to the enhancement of safety and the effectiveness of the offshore activities.

Keywords — Underwater towed cable array; cable dynamics; towed systems; towing manoeuvres; cable tension; numerical simulation; linear profile

—————————— • ——————————

1 INTRODUCTION

NDERWATER towed systems are widely used for many marine applications (naval defense, oceanograph- ic and geophysical measurements etc.). In naval appli-
cations, it is used for acoustic detection of submerged
targets. In geophysical applications, it is used for oil-
prospecting. These systems can be as simple as a single
cable with its towed vehicle, or they may be composed of
multiple towed cables and multiple towed bodies. A typi-
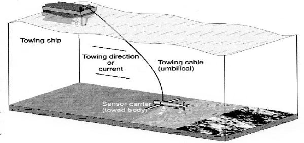
cal component of a towing system is shown in Fig 1. It is well known that the equations of motion for the cable and towed vehicle are non-linear and their dynamic behaviors during various operations are mutually dependent. As a result, these equations are strongly coupled. In order to study the complete problem, they must be solved simul- taneously as a whole. It is not easy to solve such a com- plicated problem analytically and hence numerical me- thods are usually employed. The most prevalent ap- proaches used in determining the hydrodynamic perfor- mance of a cable in an underwater towed system are the lumped mass method [1] and the finite difference method [2]-[10]. However, according to [5] the explicit time do- main integration scheme used in the lumped mass me- thod made the method conditionally stable. Burgess [6] pointed out that the time integration used in this algo- rithm requires the time step to be chosen so that the Cou- rant-Friedrichs-Levy wave condition is satisfied for the highest natural frequency of the lumped mass system. This restricts the use of very small time steps. However,

————————————————

Y Vineet Kumar Srivastava, Mohammad Tamsir

Department of Mathematics, The ICFAI University, Dehradun, India

E-mail: vineetsriiitm@gmail.com , tamsiriitm@gmail.com

Y YVSS Sanyasiraju

Department of Mathematics, IIT Madras, Chennai, India

E-mail: sryedida@iitm.ac.in

Thomas and Hearn [7] believed that the collapse of the- numerical procedure at large time steps in the method is not due to the instability of the numerical scheme, but is caused by the failure of the Newton- Raphson iterative procedure adopted to determine the correct tension levels to solve the nonlinear equations of motion.
Fig 1: Components of a towing system.
The reason for the collapse of the numerical procedure in the lumped mass method may not be clear, however it is true that time steps in this method must be chosen very small in order to avoid the failure in numerical procedure on the basis of experiences (Burgess [6]; Thomas and Hearn [7]). In the finite difference method, the governing equations for the underwater cable are derived from the balance of forces at a point of cable. Among various finite difference methods, the model developed by Ablow and Schechter [2] is worthy to note. In this model, the cable is treated as a long thin flexible circular cylinder in arbitrary motion. It is assumed that the dynamics of cable are de- termined by gravity, hydrodynamic loading and inertial forces. The governing equations are formulated in a local tangential-normal coordinate frame which has the un-

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 2

ISSN 2229-5518

stretched distance along the cable. The differential equa-
and various parameters are evaluated at all spatial grid
tions are then approximated by finite difference equations centered in time and in space. By solving the equations,
points s j
and temporal grid points ti .
the motion of underwater cable can be determined in the time domain. The principal advantage of this method is that it uses implicit time integration and is stable for large
The dynamic problem formulation is obtained by apply-
ing Newton’s second law of motion to the cable element of infinitesimaly stretched length dS .

time step sizes. It is a good algorithm for simulation of
aB aT

+ F

+ F ,

large-scale underwater cable motion.

w d

at aS

In this paper a three-dimensional hydrodynamic model to
simulate an underwater towed system is presented. In the
where B

is the momentum per unit length, T is the ten-
model, the governing equations of cable are established based on the method of Ablow and Schechter [2]. The six
sion,
and

Fw is the weight minus buoyancy per unit length

Fd is the force exerted by the fluid on the cable-array

degrees-of-freedom equations of motion for submarine
simulations are adopted to predict the hydrodynamic
performance of a towed vehicle. The established govern- ing equations are then solved using a central finite differ-
system per unit length and is taken to be the sum of inde- pendently operating normal drag and tangential. A sys- tem of three scale equations is obtained by separating the
three components of vector equation in the independent
ence method. The solution of finite-difference form of the
assembly of non-linear algebraic equations is obtained by the Newton’s method. Gauss elimination with partial
pivoting is applied to solve the linear system obtained by
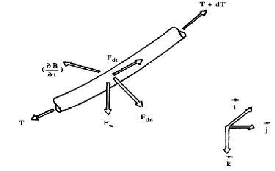
directions (t , n, b ) . The cable orientation is given in the
Fig 3.
The compatibility relations in terms of velocity are
Newton’s method. Since, the model uses implicit time
a ar
a ar
integration; it is stable for large time steps. It also gives more flexibility in choosing different time steps for differ- ent manoeuvering problems, and is an effective algorithm for the simulation of a large-scale towed system.

2 MATHEMATICAL MODEL

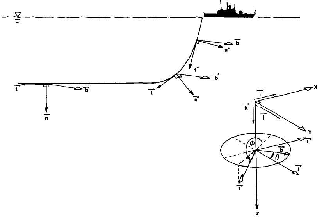
A mathematical model of manoeuvring of underwater towed cable array system [11] is used to find out the loca- tion and tension at any point on the cable as a function of time. The system is treated to be moving under the action of gravity, tow-ship, hydrodynamic loading and inertia forces. The loading function is taken to be the sum of in- dependently operating normal and tangential drags. All these forces are shown in Fig 2.

( ) ( ), (1)

at as as at
Fig 3: The Orientation of the Cable.
where r is a position vector from the origin of a fixed

coordinate system (i , j , k ) to a point on the cable-array system. r is a function of unstretched cable-array system-
length coordinate s and the time t. By separating various
components of the equation (1) in independent direc-
Fig 2: Forces Considered on a Strained System Element of length dS .
The dynamic model is a finite difference approximation
tions (t , n, b ) , a system of three scalar equations of com- patibility is obtained. Three equations of motion and
three equations of compatibility together present six sca-
lar dynamic differential equations of first order in space variable s and time variable t .
The six governing equations of motion in matrix form are

to the three dimensional differential equations for conser-
ay ay

M N + q

(2)
vation of momentum. The total length of the cable-array
system is discretized into a number of segments of arbita-
ry length. The time is divided into a number of intervals
as at

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 3

ISSN 2229-5518

( T )

t. time t holding s fixed; U
(U t , U n , Ub ) is tangential,

I IVt

normal and binormal components of cable structural ve-
locity relative to current velocity (V J ) ;

x, y, z are trail,

where y (s, t )

IVn IV I b

lateral shift and depth of a point on cable w.r.t. tow-point in the inertial frame; B (s, t ), (s,t) Euler’s angles defining
IB the position of local reference frame (t , n, b ) relative to the

\ )

r1 0 0 0 0 0 l

inertial frame (i , j , k ) .
Three boundary conditions at the tow-point of the cable are provided by known velocity components of the tow-

0 1 0 0

Vb cos

ship at any time. i.e.

0 0 1 0

V sin V

V (0, t )

v (t ), (3)

M ( y , s , t ) b t

0 0 0 1

Vn sin Vt cos 0

N( y, s, t)

r Vt

0 0 0 0 0

T J

r0	1	0	0	0 0l
0	0	1	0	0 0 y(0, t ) v (t ),

0 0 0 1 0 0J

1+ eT

0 0 0 0 0

At the free end the three boundary conditions can be ex-
pressed as

0 0 0 0 0 1+ eT

0 0 0 0

(1+ eT) cos

0 C y (S , t ) + B( y ( S , t ), t ) y ( S , t ) + Q( y( S , t ), t ) 0, (4)

(mV pAJ )

e 1 b b 0 0

m (mV pAJ ) sin mV cos 0

1+ eT

1 1 n n t

where

e (m1Vn pAJn ) 0 m 0

(mV pAJ ) sin mV

1 1 b b t

0 0 0 0 0 0

r 1

w s in + p d (1 + e T ) 2 7 C U

| U |

r0 0 0 0 0 0 l

t t t

B 0 0 m

0 (mV pAJ )sin mV cos

0 ,

0 1 1 n n t

q ( y , s , t ) 0 r l

1 1

1 p d (1 + e T ) 2 C U

(U 2 + U 2 ) 2 p A J 0

n n n t b 1 1

1 1 Q

1 p d (1 + eT ) 2 C U
(U 2 + U 2 ) 2 p AJ ,

p d (1 + e T ) 2 C U

(U 2 + U 2 ) 2 p A J

n n n t b

n n n t n

2 J 1 1 1

where A is the cross section area of unstretched cable;

p d (1 + eT ) 2 C U

(U 2 + U 2 ) 2 p AJ

Cn and

Ct are normal and tangential drag coefficients;

At t
0 , it is assumed that the initial condition is known

d is diameter of cable; p is fluid density; dS is infinite-

i.e

y (s, 0) is a known function of s (0 5: s 5: S ) . This condi-

simal stretched cable length; e
1

, E is Young’s mod-

tion along with six boundary conditions provides the complete solution of the governing equations. Computations start from a steady state solution (more
ulus; m is mass per unit length of cable; m1

m + p A is

precisely, the tow-ship is assumed to move with constant
virtual mass per unit length; w
( m p A) g is immersed
velocity), which is taken as the initial condition for the
weight per unit length; g is gravitational acceleration;

T is cable tension magnitude; v is velocity of tow-ship;

whole system.
The variables T and are determined from equations

J ( J t , J n , J b ) is current velocity given in local frame

1
T ' w sin + p d (1 + eT ) 2 7 C U
| U |
(t , n, b ) ; J

( J t , J n , J b ) is the partial derivative of J w. r. 2

t t t

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 4

ISSN 2229-5518

1 1 dure starts with the cable array length discretization and

T ' w cos

1
+ p d (1 + eT ) 2 C U
(U 2 + U 2 ) 2
time division, followed by writing of finite difference

n n n b

2
Since T ( S ) 0 , the critical angle ( S ) must satisfy

1 1

scheme for governing equations at all the nodes and the boundary conditions. All these equations are assembled.
The solution of this finite-difference form of the assembly

w cos

1
+ p d (1 + eT ) 2 C U
(U 2 + U 2 ) 2 0
of non-linear algebraic equations is obtained by Newton’s

n n n b

2
where T ' is the partial derivative of T w.r.t. s , holding t fixed; ' partial derivative of w.r.t. s , holding t fixed.
The position (x, y, z) of the cable, in the inertial frame, are
obtained from the relations

x' (1 + eT ) cos B cos ,

y' (1 + eT ) sin B cos ,

z' (1 + eT ) sin ,

method.

3 NUMERICAL APPROACH

Second order central finite difference method is applied to the governing differential equations to convert them into the algebraic difference approximations.
The total cable-array length S is divided into N segments of arbitrary length
Integrations in s determine ( x, y , z ) when eT and the

0 s0 < s1 < s2 < ........ < s N 1 < sN S .

angles B and are known.
The discrete approximation to

y (s j , ti ) is taken to be Y

If we put
with i
( , )

Y j ;: y s j ti

. For convenience the following nota-

r Vt t + Vn n + Vb b

then Vt , Vn , Vb are obtained from the relations
tions are used.

i i i i

Vt V1 cos B cos

V2 sin B cos

V3 sin ,

Y (Y0 , Y1 , ........., YN )

t [t +

+ t ],
t =t
-t ,

Vn V1 cos B sin

+ V2 sin B sin

V3 cos

i + 1 i 1

i i +1 i

Vb V1 sin B + V2 cos B 1

where

ax
ay az

s 1 [ s j +1

j + 2 2

s j ],

s =s j +1 -s j ,

V1 , V2

, V3 ,
Discretizing the governing equations of motion
at at at
ay ay

M N q 0,

The angle B is computed from the relation
as at
B tan

1 (V2 )

At the half-grid points
( j+ 1,i+ 1 ) and dropping second
2 2

V and higher order terms, we get

1 i i i +1 i

1 Y Y Y Y

Jt , J n , Jb are computed from the relations

[ M i

j +1

(

j i +1

) + M (

j +1 j

)]

1 1

2 j +
s j

j + s j

Jt J1 cos B cos

J 2 sin B cos

J3 sin , 2 2

1 i i

1 i +1 i

J n J1 cos B sin

+ J 2 sin B sin

J 3 cos

1 i +
[ N 2 (

Y j +1

) + N

i + Yj +1 Y j

( )]

2 t

j +1

Jb J1 sin B + J 2 cos B

1 [qi

i i

+ qi +1 ] 0, (5)

where

J1 ,

J 2 and

J3 are the current velocities in the

2 j + 1

j + 1

inertial frame.

Similarly, Ut , U n , Ub are computed from the relations

2 2

Denoting the LHS of the equation (5) by

i +1 , we get the

U t (V1

J1 ) cos B cos (V2

J 2 ) sin B cos (V3

J3 ) sin ,

difference approximation

i + 1

U n (V1

J1 ) cos B sin

+ (V2

J 2 ) sin B sin (V3

J 3 ) cos

<1 2
0, j=0,1,.......,N-1; (6)

U b (V1

J1 ) sin B + (V2

J 2 ) cos B

j +

to the governing equations.
Three components of the tow-ship velocity, free end zero tension along with subsequent two more free end boun-
Similarly, the boundary conditions are approximated by

i + 1

dary conditions provide a total of six requisite boundary

<10 2

DY i +1

v (ti +1 ), (7)

conditions. The solutions of the six governing equations

i + 1

Y i +1 Y i

i+ 1

along with six boundary conditions provide dynamic

<1N 2

CY i +1

+ B(YN

2 , t

)[ N N ] + Q(Y

2 , t

1 ) 0, (8)

i +

response of the cable array system. The solution proce-

2 i 2

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 5

ISSN 2229-5518

The three equations (6), (7) and (8) can be written together as

i + 1

<1 2 (Y i +1 , Y i ) 0, (9)

discussed. In the towed cable-array model, the steady ocean current (0.5 m/s) is taken.

4.1 Six Segment Cable model

where

i + 1

Here we discuss unsteady-state behavior of the cable dur- ing the ship manoeuvring for three different oceanic cur-
<1 2
(<1

2 , <1

2 , ........, <1

2 , <1

2 ),

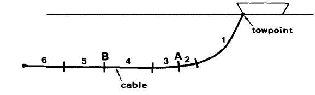
rent conditions, using the developed code. Fig 4 illu-

0 1 3

N 3 N 1 N

strates the towed array system while Table 1 gives the

2 2 2 2

The system (9) is an implicit, centered, second order ap- proximation to the system of hyperbolic pdes. Given Y i

i +1

physical characteristics of each segment of six segment cable model.
at time ti , the system of equations (9) determine Y at

ti +1 . Further we assume that the initial state of the cable

Y 0 is known.

The non-linear algebraic equations (9) are solved by itera- tion in the time domain using Newton’s method. The pre- cise algorithm of Newton’s method is given below.
Fig 4: Six Segment Towed Array System.

Table 1: Tow Cable System Physical Properties.

(a) Obtain an estimate for

Y i 1 and Y i , i.e.

Y i +1 by extrapolating

Seg ment
Length
(m)
Diamter
(m)

Weight Ct Cn

(N/m)

i + 1

<1 2 Y

i + 1

<1 2

6 30.48 0.025400 0.569134 0.02168 1.8

where

i + 1

a<1 2

4.2 Dynamic state analysis

Dynamic state analysis of underwater towed-cable is dis-

i +

<1 2

aY i +1

is the Jacobian of the above system.
cussed when tow-ship changes its speed in a fixed direc- tion (i.e., transient behavior) making linear profile. Com- putations start from a steady state solution which is taken as the initial condition for the dynamic state solution.

(c)

Y i +1

Y i + Y

gives the improved value of Y i +1 .
(d) If the absolute value of maximum relative change in any component of the solution Y i +1 is less than

Linear Profile

Here we assume that the tow-ship changes its speed along the x-direction in a straight line path. This means that the tow-ship changes its speed along a straight line path in each time step. The linear profile is given by
10 3 , increment the time and go to step (a), oth-

v (v f

v0 )(t / T ) + v0 , (10)

erwise repeat (b) and (c) using new value of Y i +1 .
where v and v are the tow-ship’s initial and final speeds,

0 f

The iteration is observed to converge quadratically. In step (a), using Y i as the initial guess for Y i +1 is sufficient to achieve convergence. Gauss elimination with partial pivoting is applied to solve the linear system.

4 RESULT AND DISCUSSIONS

The developed Newton’s scheme is implemented on the underwater towed cable-array model. The underwater towed cable-array system is discussed under a six seg- ment model, in which dynamic analysis of towed cable is
respectively, and T is the elapsed time taken to reach the final speed.

Case (i): When tow-ship accelerates from 4 to 12 m/s in a linear profile

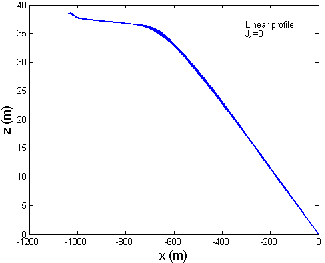
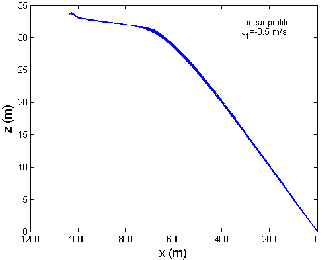
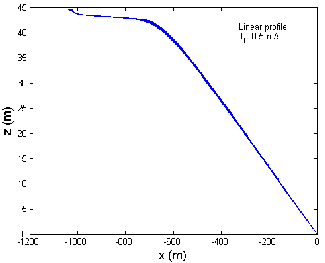
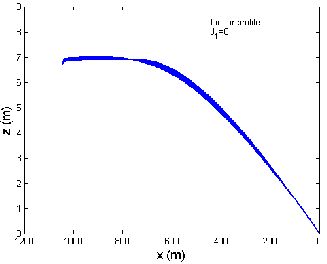
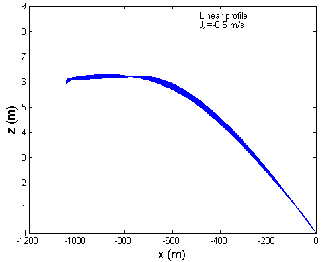
Fig 5 shows the graph between the trail and the cable depth when the tow-ship accelerates from 4 to 12 m/s in a linear profile, when there is no current, against and along the current directions respectively. The cable depth varies from 38.5 to 38.6 m, 33.6 to 33.8 m and 44.4 to 44.5 m, when the tow-ship accelerates, when there is no cur-

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 6

ISSN 2229-5518

rent, against and along the current directions, respectively as shown in Fig 5 (a), (b), (c). Thus for three different cur- rent situations, the cable depth varies in the range 33.6 to
44.5 m when the tow-ship accelerates from 4 to 12 m/s along the x-direction. It is observed that maximum cable depth occurs when the tow-ship accelerates along the current direction and minimum cable depth occurs when the tow-ship accelerates against the current direction.
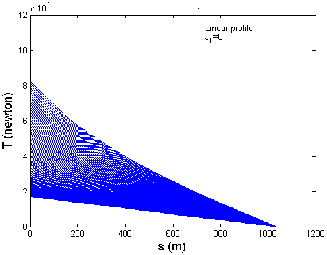
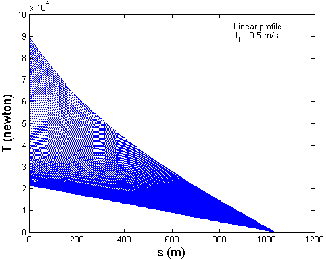
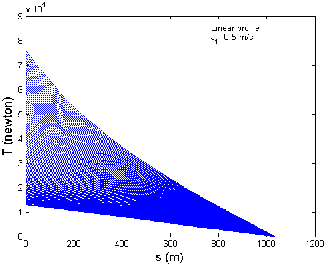
Fig 6 shows the graph between cable length and tension when the tow-ship accelerates from 4 to 12 m/s in a linear profile, (a) when there is no current, (b) against current direction and (c) along the current directions, respective
ly. The tow-point tension varies from 17.0 to 82.8 kN, 21.5
to 89.8 kN and 13.1 to 76.3 kN, when the tow-ship accele-
rates, when there is no current, against and along the cur- rent directions, respectively as shown in Fig 6 (a), (b) and (c). Thus for three different current situations, the tow- point tension varies in the range 13.1 to 89.8 kN when the tow-ship accelerates from 4 to 12 m/s along the x- direction. It is observed that maximum tow-point tension occurs when the tow-ship accelerates against the current direction and minimum tow-point tension occurs when
the tow-ship accelerates along the current direction.

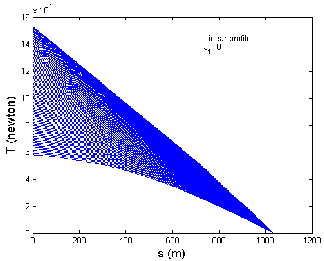
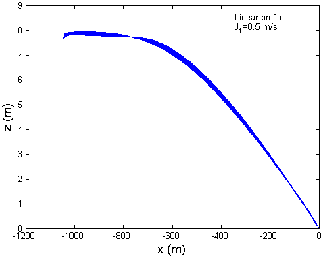
Case (ii): When tow-ship decelerates from 12 to 4 m/s in linear profile

Fig 7 shows the graph between the trail and the cable depth when the tow-ship decelerates from 12 to 4 m/s in a linear profile, when there is no current, against and along the current directions, respectively. The cable depth varies from 6.7 to 6.9 m, 5.9 to 6.1 m and 7.7 to 7.9 m, when the tow-ship decelerates, when there is no current, against and along the current directions, respectively as shown in Fig 7 (a), (b) and (c). Thus for three different current situations, the cable depth varies in the range 5.9 to 7.9 m when the tow-ship decelerates from 12 to 4 m/s along the x-direction. It is observed that maximum cable depth occurs when the tow-ship decelerates along the current direction and minimum cable depth occurs when the tow-ship decelerates against the current direction.

Case (iii): When tow-ship accelerates from 4 to 12 m/s thereafter decelerates from 12 to 4 m/s in linear profile

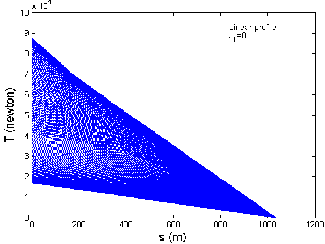
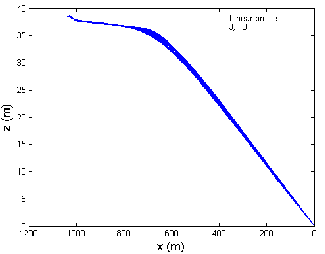
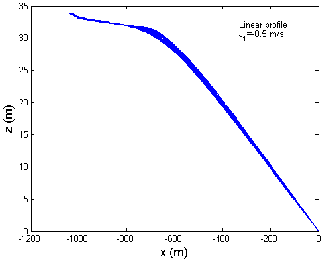
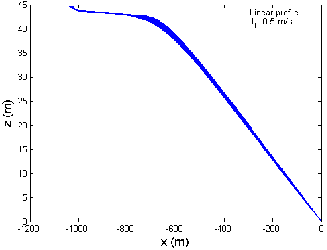
Fig 9 shows the graph between the trail and the cable depth when the tow-ship accelerates from 4 to 12 m/s thereafter decelerates from 12 to 4 m/s in a linear profile, when there is no current, against and along the current directions, respectively. The cable depth varies from 38.4 to 38.5 m, 33.6 to 33.8 m and 44.4 to 44.5 m, when the tow- ship accelerates and decelerates, when there is no current, against and along the current directions, respectively as shown in Fig 9 (a), (b) and (c). Thus for three different current situations, the cable depth varies in the range 33.6 to 44.5 m when the tow-ship accelerates from 4 to 12 m/s and then decelerates from 12 to 4 m/s along the x- direction. It is observed that maximum cable depth occurs when the tow-ship accelerates and decelerates along the current direction and minimum cable depth occurs when the tow-ship is accelerating and decelerating against the current direction.
Fig 10 shows the graph between the cable length and ten-
sion when the tow-ship accelerates from 4 to 12 m/s the-
reafter decelerates from 12 to 4 m/sec in a linear profile,
when there is no current, against and along the current
directions, respectively. The tow-point tension varies from 17.0 to 40.9 kN, 21.5 to 48.2 kN and 13.1 to 33.9 kN, when the tow-ship accelerates and decelerates, when there is no current, against and along the current direc- tions respectively as shown in Fig 10 (a), (b) and (c). Thus for three different current situations, the tow-point ten- sion varies in the range 13.1 to 48.2 kN when the tow-ship accelerates from 4 to 12 m/s and then decelerates from 12 to 4 m/s along the x-direction. It is observed that maxi- mum tow-point tension occurs when the tow-ship accele- rates and decelerates against the current direction and minimum tow-point tension occurs when the tow-ship accelerates and decelerates along the current direction.

Table 2: Cable depth Range (m) in Linear Profile. Speed Linear Profile

Fig 8 shows the graph between cable length and tension

J1 0

J1 0.5

when the tow-ship decelerates from 12 to 4 m/s in a li-
near profile, when there is no current, against and along
4 - 12 m/s 38.5 - 38.6 33.6 - 33.8 44.4 - 44.5
12 - 4 m/s 6.7 - 6.9 5.9 - 6.1 7.7 - 7.9
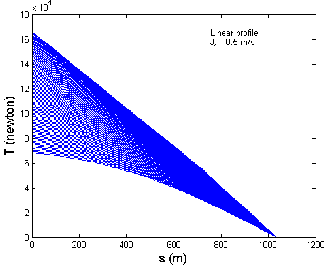
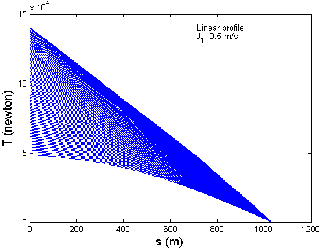
the current directions, respectively. The tow-point tension
varies from 58.1 to 153.2 kN, 68.3 to 166.3 kN and 48.6 to
140.7 kN, when the tow-ship decelerates, when there is no
current, against and along the current directions, respec-
4 - 12m/s &
12 - 4 m/s
38.4 - 38.5 33.6 - 33.8 44.4 - 44.5
tively as shown in Fig 8 (a), (b) and (c). Thus for three different current situations, the tow-point tension variesin

Table 3: Tow-point Tension Range (kN) in Linear Profile.

Speed Linear Profile
the range 48.6 to 166.3 kN when the tow-ship decelerates

J1 0

J1 0.5

from 12 to 4 m/s along the x-direction. It is observed that
maximum tow-point tension occurs when the tow-ship
4 - 12 m/s 17.0 - 82.8 21.5 - 89.8 13.1 - 76.3
12 - 4 m/s 76.3 - 153.2 68.3 -166.3 48.6 -140.7
decelerates against the current direction and minimum
tow-point tension occurs when the tow-ship decelerates
along the current direction.
4 - 12 m/s &
12 - 4 m/s
17.0 -40.9 21.5 - 48.2 13.1 -33.9

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 7

ISSN 2229-5518

(a) When there is no current.

(b) Against the current direction.
(c) Along the current direction.

Fig 5: Graph between the Trail and the Cable Depth when

the Tow-Ship Accelerates from 4 to 12 m/s in
Linear Profile: (a), (b), (c).

(a) When there is no current.

(b) Against the current direction.
(c) Along the current direction.

Fig 6: Graph between the Cable length and Tension when

the Tow-Ship Accelerates from 4 to 12 m/s in
Linear Prfile: (a), (b), (c).

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 8

ISSN 2229-5518

(a) When there is no current.

(b) Against the current direction.

Fig 7: Graph between the Trail and the Cable Depth when the Tow-Ship Decelerates from 12 to 4 m/s in Linear Pro- file: (a), (b), (c).

(a) When there is no current.

(b) Against the current direction.
(c) Along the current direction.

Fig 8: Graph between the Cable length and Tension when

the Tow-Ship Decelerates from 12 m/s to 4 m/s in Linear
Profile: (a), (b), (c):

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 9

ISSN 2229-5518

(a) When there is no current.

(b) Against the current direction.
(c) Along the current direction.

Fig 9: Graph between the Trail and the Cable Depth when

the Tow-Ship Accelerates from 4 to 12 m/s then Decele-
rates from 12m/s to 4 m/s in Linear Profile: (a),(b),(c).

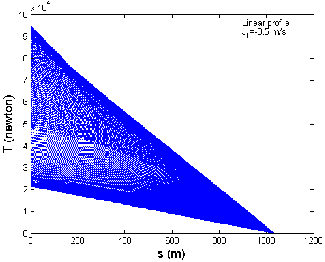
(a) When there is no current.

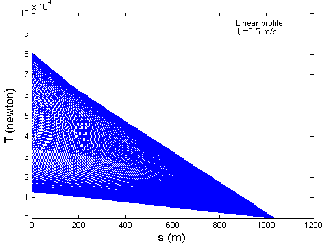
(b) Against the current direction.
(c) Along the current direction.

Fig 10: Graph between the Cable length and Tension when the Tow-Ship Accelerates from 4 to 12 m/s then Decelerates from 12m/s to 4 m/s in Linear Profile: (a),(b),(c).

International Journal of Scientific & Engineering Research Volume 2, Issue 7, July-2011 10

ISSN 2229-5518

5 CONCLUSION

In this study, a three-dimensional numerical program is developed for the analysis of the underwater towed ca- ble-array system when tow-ship makes linear profile dur- ing manouring. An implicit finite difference method is employed for solving the three dimensional cable equa- tions. In order to solve the non-linear and coupled prob- lems, Newton’s iteration scheme is used, and satisfactory results are obtained. The developed numerical program can be applied to towed array systems for detecting a moving object or submarine.

REFERENCES

[1] T. S.Walton, H. Polacheck, “Calculation of Transient Motion of

Submerged Cables,” Math. Comput 14(1960) 27-46.

[2] C.M. Ablow and S.Schechter, “Numerical simulation of und sea cable dynamics,” Ocean Engng, 10(1983) 443-457.

[3] F. Milinazzo, M.Wilkie and S.A. Latchman, “An efficient algo-

rithm for simulating the dynamics of the towed cable systems,” Ocean Engng, 14(1987) 513-526.

[4] Thomas N. Delmer, Thomas C. Stephens, James A. Tremills, “Numerical Simulation of Cable-Towed Acoustic Arrays,” Ocean Engng, 15(1988) 511-548.

[5] M. A. Grosenbaugh, C. T. Howell, S. Moxnes, “Simulating the Dynamics of Underwater Vehicles with Low-Tension Tethers,” Int. J. Offshore Polar Engg, 3(1993) 213-218.

[6] Burgess, J.J., “Modelling of undersea cable installation with a finite difference method,” Proceedings of the 1st International Offshore and Polar Engineering Conference, I-A (1992) 283-288.

[7] D. O. Thomas, G. E. Hearn, “Deepwater Mooring Line Dynam- ics With Emphasis On Seabed Interference Effects,”Proceedings of the 26th Offshore Technology Conference, II-A (1994) 203-

214.

[8] M. A. Vaz, M. H. Patel, “Transient behaviour of towed marine cables in two dimensions,” Applied Ocean Research, 16 (1995)

143-153.

[9] M. A. Vaz, M. H. Patel, “Three dimensional transient analysis of the installation of marine cables,” Acta Mechanica, 124 (1997)

1-26.

[10] J.I. Gobat, M.A. Grosenbaugh, “Time- domain numerical simu- lation of ocean cable structures,” Ocean Engng, 10(2006) 1373-

1400.

[11] Choo, Y-I., Casarella, M.J., “A survey of analytical methods for dynamic simulation of cable-body systems,” J. Hydronautics,

7(1973) 137-144.