ceramic processing, sensible heat storage beds and petroleum
the conservation of mass, momentum, energy and concentrations are:
recovery etc., In view of the aforesaid applications, many
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 83
ISSN 2229-5518
Double Dispersion effects on free convection
along a vertical Wavy Surface in Porous Media with Variable Properties
R. Bhuvanavijaya, B. Mallikarjuna
—————————— ——————————
n recent years, the study of natural convective flow, heat and mass transfer in porous media has received considerable interest in the literature. The interest for such studies is motivated by grain storage insulations, nuclear waste disposal, oil extraction, ground water pollution, resin transfer modeling, dispersion of chemical contaminants through water – saturated soil, fibrous insulations, packed beds and geo thermal systems. Comprehensive reviewers of the convection through Darcy porous media have been reported by Nield and Bejan [1] and by Ingham and Pop [2]. Darcy’s law states that the volume averaged velocity is proportional to the pressure gradient. The present study deals with free convective flow on a vertical wavy surface embedded in a saturated porous medium. Natural convection from wavy surfaces is a topic of fundamental importance in heat transfer devices, such as flat-plate solar collectors and flat-plate condensers in refrigerators. Mainly, roughness elements disturbs the flow and alters the rate of heat and mass transfer, this is type of irregularities mostly occur in manufacturing. At first, Rees and Pop [3] investigated free convection along a vertical wavy surface in a porous medium. Cheng [4] studied natural convection heat and mass transfer near a vertical wavy surface with constant wall temperature
————————————————
(* Corresponding author: B. Mallikarjuna)
and concentration in a porous medium.
Recently, Shalini and Rathish Kumar [5] investigated the influence of variable heat flux on natural convection along a corrugated wall in porous media. Mohamed et.al [6] studied combined radiation and free convection from a vertical wavy surface embedded in porous media. Elgazery and Elazem [7] investigated the effects of variable properties on MHD unsteady natural convection heat and mass transfer over a vertical wavy surface. Rathish kumar and Krishan Murthy [8] analyzed Soret and Dufour effects on double diffusive free convection from a corrugated vertical surface in a non-Darcy porous medium. Neagu [9] analyzed free convective heat and mass transfer induced by a constant heat and mass fluxes vertical wavy wall in a non-Darcy double stratified porous medium. Narayana et.al. [10] studied double diffusive convection and cross diffusion effects on a horizontal wavy surface in a porous medium. Parveen and Alim [11] investigated Joule heating and MHD free convection flow along a vertical wavy surface with viscosity and thermal conductivity dependent on temperature.
The hydrodynamic mixing is called dispersion, which is the secondary effect of a porous medium on the fluid flow takes place in the result of mixing and recirculation of local fluid particles through tortuous paths formed by the porous medium solid particles. There has been renewed interest in studying double diffusive convection due to the effect of thermal and solutal dispersions; these are additional energy and concentration mass transport process. In certain thermal
and solutal dispersion applications such as those involving oil
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 84
ISSN 2229-5518
reservoir and geothermal engineering applications such as
ceramic processing, sensible heat storage beds and petroleum
the conservation of mass, momentum, energy and concentrations are:
recovery etc., In view of the aforesaid applications, many![]()
![]()
∂u ∂v
![]()
![]()
= 0
(2)
authors have analyzed the effects of thermal and solutal
∂x ∂y
dispersion on convective heat and mass transfer through![]()
∂ µ u =
![]()
∂ µ v ± ρ g β
∂T + β
∂C
(3)![]()
![]()
![]()
![]()
![]()
![]()
t c
porous media. Abbas et.al. [12] studied effects of thermal
dispersion on free convection in a fluid saturated porous
∂y K
∂x K ∂y
∂y
medium. Kairi and Murthy [13] considered the double ∂T ∂T
∂ ∂T ∂
∂T
dispersion effects to study mixed convection heat and mass transfer in a non-Newtonian fluid saturated non-Darcy porous![]()
![]()
![]()
![]()
![]()
![]()
u + v = α x + α y
∂x ∂y ∂x ∂x ∂y ∂y
(4)
medium. Pathak and Ghiaasiaan [14] investigated convective ∂C ∂C
∂ ∂T ∂
∂T
heat transfer and thermal dispersion during laminar pulsating flow in porous media. The effects of MHD and double dispersion on free convection in a non-Darcy porous medium![]()
![]()
![]()
![]()
![]()
![]()
u + v = Dx + Dy
∂x ∂y ∂x ∂x ∂y ∂y
The corresponding boundary conditions are
(5)
saturated with power law fluid are investigated by ![]()
![]()
![]()
π x
Srinivasacharya et.al [15]. Ramreddy [16] has been studied the![]()
u = 0, v = 0,T = Tw , C = Cw , at y = σ ( x ) = a sin
effects of double dispersion on convective flow over a cone.![]()
u → 0, T → T
![]()
, C → C as y →∞
l
(6)
∞ ∞
In view of the above application, the authors are
envisage to investigate free convection along a vertical wavy
where![]()
![]()
![]()
![]()
u , and v are velocity components in x and y
surface embedded in a fluid saturated porous medium with variable properties and double dispersion effects. The governing boundary equations for flow mass, momentum, energy and concentration are transformed into non- dimensional nonlinear ordinary differential equations by using appropriate transformation and then solved by using
numerical method. The results are reported graphically for
directions respectively. μ is the kinematic viscosity, K is the permeability of the porous medium, ρ is the density of the fluid, βt is the thermal expansion coefficient, βc is the solutal expansion coefficient, g is the acceleration due to gravity, αx , Dx and α y, Dy are the effective thermal and solutal diffusivities respectively, have the contribution of both molecular diffusion and hydrodynamic dispersion, these can be described as (see Telles and Trevisan [17])
various physical parameters for flow velocity, temperature![]()
α x = α + γ dv ,![]()
α y = α + γ du
(7)
and concentration distributions as well as Nusselt number and Sherwood number. The present results are compared with previously existing results and obtained a very good agreement.
We consider the steady, two dimensional laminar, viscous![]()
Dx = D + ζ dv , Dy = D + ζ du
where α is the thermal conductivity, D is the molecular diffusivities, γ is the coefficient of thermal dispersion and ζ is the solutal dispersion. The fluid properties namely, viscosity and thermal conductivities are assumed to be vary as an inverse linear and linear function of the temperature respectively and these can be written as (see [18-20])
incompressible fluid over a vertical wavy plate embedded in a
saturated porous medium. The configuration of the model and
coordinate system is shown in fig. 1. We assume that the wavy surface is given by![]()
![]()
1 = 1
µ µ ∞
(1 + δ (T − T∞ )) or
![]()
1 = b (T − T ) and α = α (1 + E(T − T ))
µ![]()
![]()
![]()
![]()
![]()
y = σ ( x ) = a sin π x
(1)
where
l 1
![]()
![]()
![]()
Where ‘a’ represents amplitude of the wavy surface and ‘l’
b = δ
µ∞
, and Tr
= T∞ − δ .
represents the characteristics of wavy length. The plate is maintained with constant temperature T w and concentration Cw, which are higher than the ambient fluid temperature T ∞ and concentration C∞ . The Darcy law can be used to describe the porous medium. In addition, we consider thermal and solutal dispersion effects. In view of the above assumptions and invoking the boundary layer and Boussinesq approximations, the governing boundary layer equations for
Both b and Tr are constants and their values depend on the reference state and the thermal property of the fluid i.e. δ, αo is the thermal diffusivity at the wavy surface temperature T w and E is a constant depending on the nature of the fluid. In general, b>0 for liquids and b<0 for gases. It is worth mentioning here that E is positive for fluids such as air and E
is negative for fluids such as lubrication oils.θ r , which is
defined by
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 85
ISSN 2229-5518
= Tr − T∞ = −1
(8)![]()
ν = µ∞
βc (Cw − C∞ )
![]()
is the kinematic viscosity of the fluid, N =![]()
![]()
θr
Tw − T∞
δ (Tw
− T∞ )
ρ![]()
is the buoyancy ratio, Le = αo
βt (Tw − T∞ )
is the Lewis number, and
is constant. The parameter θr
was first introduced by Ling D
and Dybbs [21] It is worth mentioning here that for δ → 0 (i.e.
gK βt (Tw − T∞ ) d
![]()
Rad = is the pore diameter dependent
µ = µ∞ =constant) then
θr →∞ , the effect of viscosity is
αoν
negligible. The variable thermal conductivity can be written in the non-dimensional form (see [20]) as
Rayleigh number which describes the relative intensity of the buoyancy force, such that d is the pore diameter.
α = αo (1 + βθ )
(9)
The associated boundary conditions are given by
where β=E(T w -T ∞ ) is the thermal conductivity parameter. The
ψ * = 0, θ = 1, ϕ = 1,
on y = a sin( x),
variation of β can be taken in the range
−0.1 ≤ β ≤ 0
for
*
(14)
![]()
lubrication oils, 0 ≤ β ≤ 0.12 for water and 0 ≤ β ≤ 6 for air. We define the stream functionψ , which is to be satisfied the continuity equation (2) such that![]()
![]()
![]()
![]()
u = ∂ψ , v = − ∂ψ
ψ y → 0, θ → 0 as y → ∞,
Let us consider the following transformations![]()
![]()
∂y ∂x
x = ξ ,
η = y − a sin( x) ,
ψ * = Ra 1/ 2ψ .
(15)
To convert the governing boundary layer equations in non-
ξ 1/ 2
Rax
![]()
−1/ 2 x
dimensional form, we introduce the following dimensionless variables
Invoking the eq (15) and letting Rax →∞ into eqs. (11) - (14)
reduces into the following boundary layer equations:![]()
![]()
x = x ,
![]()
![]()
y = y ,
![]()
![]()
a = a ,
![]()
![]()
σ = σ ,
1 + 2
2 ξ ∂θ ∂ψ + + 2
∂2ψ
![]()
ξ
l l l l
(10)
(1
θ − θr
a cos ( ))
∂η ∂η
(1 a
cos ( ))
∂η 2
![]()
![]()
ψ * = ψ ,
α0![]()
θ = T − T∞ ,
Tw − T∞
![]()
ϕ = C − C∞
Cw − C∞
1/ 2
= ξ
θ ∂θ ∂ψ
![]()
![]()
![]()
1 − + N
(16)
By using eqs. (7) – (10), the eqs. (3) – (5) reduces to
θ r ∂η
∂η
1/ 2 2
∂ψ ∂θ − ∂ψ ∂θ = + 2 2
+ ∂ θ
1 ∂θ ∂ψ *
∂θ ∂ψ *
∂ 2ψ *
∂ 2ψ *
θ ∂θ
∂ϕ
![]()
![]()
ξ ∂η ∂ξ
∂ξ ∂η
(1 a
cos (ξ )) (1
![]()
βθ )
∂η 2
θ − θ
![]()
![]()
∂y
![]()
+
∂y ∂x
![]()
![]()
∂x + 2 + 2
![]()
= Ra 1 − θ
![]()
![]()
∂y + N ∂y (11) 2
r ∂y ∂x
r 2 2
+ β (1 + a2 cos2 (ξ )) ∂θ
∂ ψ ∂θ ∂ψ
![]()
![]()
+ Dsξ (1 + a cos (ξ )) +
∂ θ
![]()
∂ψ * ∂θ
∂ψ * ∂θ
∂θ 2
2
∂θ ∂ θ
∂2θ
∂η
∂η 2 ∂η
∂η ∂η 2
(17)
![]()
![]()
− = β
y x x y
+
x y
+ (1 + βθ )
+
x2 y 2
∂ ∂ ∂ ∂
∂
∂
∂ ∂
1/ 2 2
γ d ∂2ψ * ∂θ
∂2ψ * ∂θ
∂ψ * ∂2θ
∂ψ * ∂2θ
Leξ
∂ψ ∂ϕ − ∂ψ ∂ϕ = (1 + a2 cos2 (ξ )) ∂ ϕ
∂ ∂ ∂ ∂
![]()
![]()
![]()
![]()
![]()
+
l ∂y 2
−
∂y ∂x2
+
∂x ∂y
−
∂y 2 ∂x
∂x2
(12)
![]()
![]()
![]()
η ξ ξ η
∂η 2
2 2
(18)
∂ψ * ∂ϕ
∂ψ * ∂ϕ
∂2ϕ
∂2ϕ
∂ ψ ∂φ ∂ψ
![]()
![]()
+ Dc(1 + a cos (ξ )) +
∂ φ
![]()
![]()
![]()
![]()
2 2
Le −
y x
x y = x2 + y 2
∂η ∂η
∂η ∂η
∂ ∂ ∂ ∂
∂ ∂
(13)
ζ d ∂2ψ * ∂φ
∂2ψ * ∂φ
∂ψ * ∂2φ
∂ψ * ∂2φ
![]()
![]()
![]()
![]()
![]()
+ − + −
where Ds = γ .Rad is the thermal dispersion parameter
l ∂y 2 ∂y
∂x2 ∂x
∂y ∂y 2
∂x ∂x2
Dc = ζ .Rad is the solutal dispersion parameter. To transform
gK β (T − T )l
![]()
where Ra =
αoν
is the modified - Rayleigh number,
Eqs. (16) - (18) into a set of ordinary differential equations, we introduce the following similarity transformations
ηˆ =![]()
η ,
1 + a2 cos2 (ξ )
ψ = ξ 1/ 2 f (ηˆ),
θ = θ (ηˆ)
and
ϕ = ϕ (ηˆ)
(19)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 86
ISSN 2229-5518
Thus, we obtain
concentration distributions is presented in figs. (2) – (4). It is noticed from fig. (2) that an increase in variable viscosity
f ′′ +
![]()
![]()
θ ′ f ′ = 1 − (θ ′ + Nϕ′)
(20)
θ − θr
θr
![]()
![]()
β (θ ′)2 + (1 + βθ )θ ′′ + 1 f θ ′ + Ds (1 + a cos (ξ )) ( f ′′θ ′ + θ ′′ f ′) = 0
2 (1 + a2 cos2 (ξ ))2
(21)
1 1 (1 + a3 cos3 (ξ ))
![]()
![]()
![]()
ϕ′′ + f ϕ′ + Dc ( f ′′φ′ + φ′′ f ′) = 0
Le 2 (1 + a2 cos2 (ξ ))2
(22)
where prime denotes differentiation with respect to ηˆ .
The associated boundary conditions are
f = 0,
θ = 1,
and
ϕ = 1
at ηˆ = 0
(23)
f ′ → 0,
θ → 0
and
ϕ → 0
as ηˆ →∞
The engineering design quantities of physical interest include
Nusselt number and Sherwood numbers which are defined as
f ′(0)
θ ′(0)Raξ1/ 2
![]()
![]()
Nuξ = − 1 + Ds (1 + a2 cos2 (ξ )) (1 + a2 cos2 (ξ ))1/ 2
(24)
f ′(0)
ϕ′(0)Raξ1/ 2
![]()
![]()
and Shξ = − 1 + Ds (1 + a2 cos2 (ξ )) (1 + a2 cos2 (ξ ))1/ 2
The problem of free convection along a vertical wavy surface embedded in fluid saturated Darcy porous media subject to the variable viscosity, variable thermal conductivity and double dispersion effects has been investigated. A simple coordinate transformation is employed to reduce the governing non-linear boundary equations into non-linear ordinary differential equations and then employed Runge-Kutta method with shooting technique. We restrict the physical parameter values
1<θr ≤ 5, 1≤β≤5, 0<Ds≤1, 0<Dc≤1, and 0.5≤ξ≤2 with the fixed
values N=1, Le=1 and a=0.5. In order to validate the present
method the numerical results obtained using the Runge Kutta
method with shooting method are compared with Cheng [22]
results. Table-1 shows the comparison results in the absence of
variable properties and double dispersion effects (i.e. Ds=0 and
Dc=0) over vertical wavy surface with Cheng [22] and the
results are found to be in good agreement.
We have found the numerical solutions for non dimensional velocity, temperature and concentration distributions as well as rate of heat and mass transfer coefficients as shown graphically in Figs. (2) – (24). The variation of variable viscosity parameter
(θr ) on non-dimensional velocity, temperature and
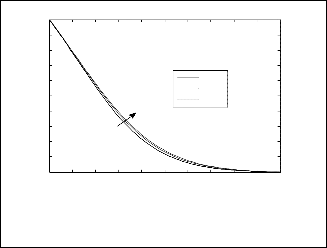
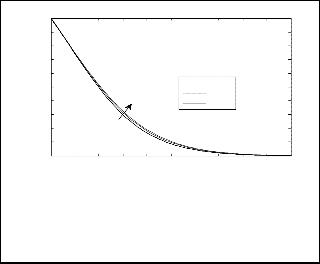
parameter θr resulted in depreciation in velocity distribution
near the plate up to reach certain value and then increase the
velocity profile until approaches a constant value (zero) at outer
boundary layer regime. From figs. (3) and (4) we conclude that
increasing variable viscosity parameter θr , clearly substantially enhances the temperature and concentration distributions.
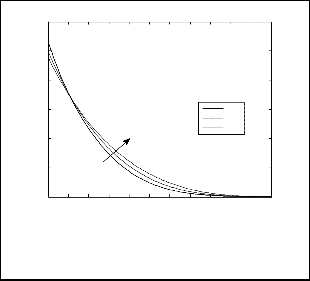
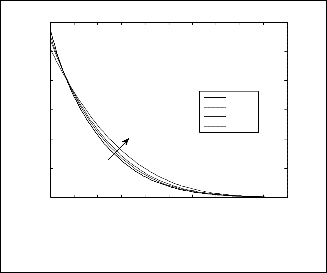
The variation of variable thermal conductivity (β) on velocity, temperature and concentration distributions is illustrated in figs. (5) – (7). The velocity profile results for different values of β are given by fig. (5), these results are having similar behavior as shown in fig. (2). From fig. (6) it is evident that temperature profiles is more pronounced with increasing values of β. Conversely, a strong decrease in concentration distribution as shown in Fig. (7); occurs with increasing values of β.
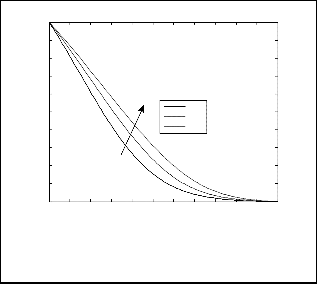
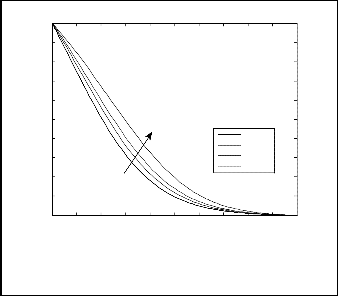
The effect of thermal dispersion parameter (Ds) on the non- dimensional velocity, temperature and concentration is depicted in figs. (8) – (10). From fig. (8) we conclude that the results of velocity profile reduce near the surface for larger values of thermal dispersion parameter and opposite results are observed as the radial distance moves far away from the surface with increase in thermal dispersion parameter. The presence of thermal dispersion in the energy equation gives thermal conduction more dominance. It is observed from fig. (9) that increasing thermal dispersion parameter tends to enhance the temperature distribution. i.e. thermal dispersion enhances the transport of heat along radial direction to the plate. It is noticed
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 87
ISSN 2229-5518
from fig. (10) that the solutal boundary layer thickness is reduced as increase in thermal dispersion parameter.
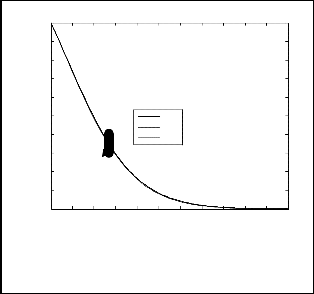
The set of figs. (11) – (13) are plotted for the variation of non- dimensional velocity, temperature and concentration distributions across the boundary layer for different values of solutal dispersion parameter (Dc). From fig. (11) we noticed that an increase in Dc is seen to significantly enhance the momentum boundary thickness. It is observed from fig. (12) that temperature profile reduced with increase in Dc. It can be evident from this figure that as Dc increases thermal boundary layer thickness increases. It is observed from fig. (13) that increasing the solutal dispersion parameter (Dc), accelerates the concentration of the fluid. Hence the concentration boundary layer thickness increases with an increase in solutal dispersion parameter (Dc).
Figs. (14) – (16) illustrate the velocity, temperature and concentration distributions for different values of ξ-location. It can be found from fig. (14) that velocity profile is increased with increase in ξ-location. Hence the hydrodynamic boundary layer thickness increases as increase in ξ-location. We noticed from figs. (15) and (16) that the similar behavior of temperature and concentration profile, in comparison with velocity distribution as shown in fig. (14). It is an important to note that it quickly reaches similarity solutions not far away from the leading edge.
The variation of rate of heat and mass transfer (Nusselt number and Sherwood number) with streamwise coordinate at the wall are shown in figs. (17) – (18) for different values of variable viscosity parameter (θr ). It is noticed from these figures that both Nusselt number and Sherwood number decreases with increase in θr . Hence, it is clear that increase in θr results an depreciation in the amplitude of the Nusselt number and Sherwood. Figs (19) – (20) represent the variation of Nusselt number and Sherwood number for different values of variable thermal conductivity parameter (β). Figs. (19) – (20) demonstrates that Nusselt number and Sherwood number reduces considerably for larger values of β. Figs. (21) – (22) reveals that enhancement of thermal dispersion parameter results enhancement in the amplitude of the Nusselt number and Sherwood number. The variation of Nusselt number and Sherwood number for different values of solutal dispersion parameter (Dc) is given in figs. (23) – (24). Figs. (23) – (24) exhibits the similar behavior of Nusselt number and Sherwood with streamwise coordinate, in comparison with what observed in figs. (21) – (22). Figs. (25) – (26) illustrates the variation of Nusselt number and Sherwood number for different values of the amplitude of the wavy surface. For ‘a = 0’ the vertical wavy surface reduces to vertical flat surface. It is noticed from figs. (25) and (26) that increasing the amplitude of the wavy surface, clearly substantially enhances the amplitude of the Nusselt number and Sherwood number with streawise coordinate.
The effect of thermal and solutal dispersion on free convection along a vertical wavy surface with temperature dependent viscosity and thermal conductivity analyzed and the governing boundary non-dimensional equations are solved by
employing Runge-Kutta method with shooting technique. The main results in this study are as follows:
1. Increasing variable viscosity parameter leads to decrease velocity distribution, Nusselt number and Sherwood number while temperature and concentration distributions are increases.
2. Increasing thermal dispersion parameter tends to increase velocity and temperature distributions as well as Nusselt number and Sherwood number while opposite results are noticed for concentration profile.
3. Velocity and concentration distributions as well as Nusselt number and Sherwood number are increased with increase in solutal dispersion parameter while we noticed that opposite results are reported for temperature profile.
4. Increase in the amplitude of the wavy surface results an enhancement in Nusselt number and Sherwood number.
[1] D.A. Nield and A. Bejan, “Convection in porous media”, Newyork, Springer, 1992.
[2] D.B. Ingham and I. Pop, “Transfer phenomena in porous media”, Oxford; Pergamon; 1998
[3] D.A.S. Rees and I. Pop, “A note on free convection along a vertical wavy surface in a porous medium”, Journal of Heat Transfer, Vol. 116, pp. 505-508, May
1994.
[4] C.Y. Cheng, “Natural convection heat and mass
transfer near a vertical wavy surface with constant
wall temperature and concentration in a porous
medium”, International Communication in Heat and
Mass Transfer, Vol-27, No. 8, pp. 1143-1154, 2000.
[5] Shalini and B.V. Rathish Kumar. “Influence of
variable heat flux on natural convection along a
corrugated wall in porous media”, Communications
in Nonlinear Science and Numerical Simulation, Vol –
12, pp. 1454-1463, 2007.
[6] R.A. Mohamed, A. Mahdy, and F.M. Hady, “Combined radiation and free convection from a vertical wavy surface embedded in porous media”, International Journal of Applied Mathematics and
Mechanics, Vol – 4, No-1, pp. 49-58, 2008.
[7] N.S. Elgazery and N.Y.A. Elazem, “The effects of
variable properties on MHD unsteady natural
convection heat and mass transfer over a vertical
wavy surface”, Meccanica, Vol – 44, pp. 573-586, 2009.
[8] B.V. Rathish kumar and S.V.S.S.N.V.G. Krishan
Murthy, “Soret and Dufour effects on double
diffusive free convection from a corrugated vertical
surface in a non-Darcy porous medium”, Transport in
Porous media”, Vol – 85, pp. 117 – 130, 2010.
[9] M. Neagu, “Free convective heat and mass transfer
induced by a constant heat and mass fluxes vertical
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 88
ISSN 2229-5518
wavy wall in a non-Darcy double stratified porous medium”, International Journal of Heat and Mass Transfer, Vol – 54, pp. 2310-2318, 2011.
[10] M. Narayana, P. Sibanda, S.S. Motsa and P.G.
Siddheswar, “On double diffusive convection and
cross diffusion effects on a horizontal wavy surface in
a porous medium”, Boundary value Problems, Vol –
88, No-1, pp. 1-22, 2012.
[11] N. Parveen and M.A. Alim, “Joule heating and MHD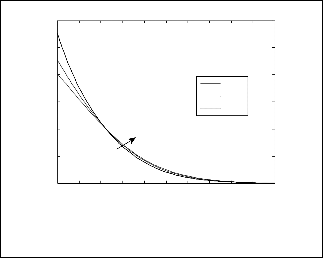
wall temperature and concentration in porous medium”, International Communications in Heat and Mass Transfer, Vol-27, No-8, pp. 1143-1154, 2000.
3
2.5
2
θ = 1.5
r
free convection flow along a vertical wavy surface with viscosity and thermal conductivity dependent on temperature”, Journal of Naval Architecture and Marine Engineering, Vol – 10, pp. 81-98, 2013.
[12] I.A. Abbas, M.F. El-Amin, and A. Salama, “Effects of thermal dispersion on free convection in a fluid saturated porous medium”, International Journal of Heat and Fluid Flow, Vol-30, pp. 229-236, 2009.
1.5
1
0.5
0
θ = 2
r
θ = 5
r
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
[13] R.R. Kairi, and P.V.S.N. Murthy, “The effects of double dispersion on mixed convection heat and mass transfer in a non-Newtonian fluid saturated non- Darcy porous medium”, Journal of Porous Media, Vol-13, No-8, pp. 749-757, 2010.
[14] M.G. Pathak and S.M. Ghiaasiaan, “Convective heat transfer and thermal dispersion during laminar pulsating flow in porous media”, International
Fig.1. Velocity profile for different values of variable viscosity
parameter for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5,β=0.5, and
ξ=1.
1
0.9
0.8
0.7
Journal of Thermal Sciences, Vol-50, pp. 440-448, 2011. [15] D. Srinivasacharya, J. Pranitha, and Ch. Ramreddy, “Magnetic and double dispersion effects on free convection in a non-Darcy porous medium saturated
with power law fluid”, International Journal of Computational Methods in Engineering Science and Mechanics, Vol-13, No-3, pp. 210-218, 2012.
[16] Ch. Ramreddy, “Effects of double dispersion on convective flow over a cone”, International Journal of
0.6
0.5
0.4
0.3
0.2
0.1
0
θ = 1.5
r
θ = 2
r
θ = 5
r
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
Nonlinear Science, Vol – 15, No-4, pp. 309-321, 2013. [17] R.S. Telles, and O.V. Trevisan, “Dispersion in heat
and mass transfer natural convection along vertical boundaries in porous media”, International Journal of Heat and Mass Transfer, Vol-36, No-5, pp. 1357-1365,
1993.
[18] EC.Lai, FA.Kulacki, “Effects of variable viscosity on
convective heat transfer along a vertical surface in a
Fig.2. Temperature profile for different values of variable
viscosity parameter for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5,
β=0.5, and ξ=1.
1
0.9
0.8
0.7
0.6
saturated porous medium”, International Journal of
Heat and Mass Transfer, Vol-33, pp. 1189-1194, 1990.
[19] M.S.Seddeek, A.M.Salem, “Laminar mixed convection
adjacent to vertical continuously stretching sheets
with variable viscosity and variable thermal
diffusivity”, Heat and Mass Transfer, Vol-41, pp.
1048-1055, 2005.
0.5
0.4
0.3
0.2
0.1
0
θ = 1.5
r
θ = 2
r
θ = 5
r
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
[20] J.C.Slattery, “Momentum, energy and mass transfer in continua” Mc. Graw-Hill, New York, 1972.
[21] J.X. Ling and A. Dybbs, “Forced convection over a flat plate submersed in a porous medium: variable viscosity case” ASME Paper 87-WA/HT Fo-23, American society of Mechanical Engineers, New York, 1987.
[22]C.Y. Cheng, “Natural convection heat and mass
transfer near a vertical wavy surface with constant
Fig.3. Concentration profile for different values of variable viscosity parameter for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5,
β=0.5, and ξ=1.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 89
ISSN 2229-5518
3 3
2.5
2.5
2 2
1.5
1
β = 1
β = 2
β = 3
1.5
1
Ds = 0.1
Ds = 0.3
Ds = 0.5
Ds = 1
0.5
0.5
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5
η
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
Fig.5. Velocity profile for different values of variable thermal conductivity parameter for N=1, Le=1, Ds=0.3, Dc=0.3,
a=0.5, θr=1.5, and ξ=1.
Fig.8. Velocity profile for different values of Ds for N=1, Le=1,
Ds=0.3, Dc=0.3, a=0.5, θr=1.5, β=0.5, and ξ=1.
1 1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
β = 1
β = 2
β = 3
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5
η
0.6
0.5
0.4
0.3
0.2
0.1
0
Ds = 0.1
Ds = 0.3
Ds = 0.5
Ds = 1
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
Fig.6. Temperature profile for different values of variable thermal conductivity parameter for N=1, Le=1, Ds=0.3,
Dc=0.3, a=0.5, θr=1.5, and ξ=1.
Fig.9. Temperature profile for different values of Ds for N=1, Le=1,
Ds=0.3, Dc=0.3, a=0.5, θr=1.5, β=0.5, and ξ=1.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
β = 1
β = 2
β = 3
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5
η
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Ds = 0.1
Ds = 0.3
Ds = 0.5
Ds = 1
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
Fig.7. Concentration profile for different values of variable thermal conductivity parameter for N=1, Le=1, Ds=0.3,
Dc=0.3, a=0.5, θr=1.5, and ξ=1.
Fig.10. Concentration profile for different values of Ds for N=1,
Le=1, Ds=0.3, Dc=0.3, a=0.5, θr=1.5, β=0.5, and ξ=1.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 90
3
4.5
4
2.5
2
1.5
1
Dc = 0.1
Dc = 0.3
Dc = 0.5
Dc = 1
3.5
3
2.5
2
1.5
ξ = 0.5
ξ = 1
ξ = 1.5
0.5
1
0.5
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
0
0 0.5 1 1.5 2 2.5 3 3.5 4
η
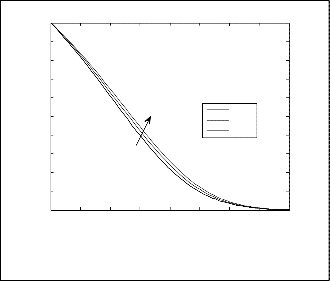
Fig.11. Velocity profile for different values of Dc for N=1, Le=1,
Ds=0.3, a=0.5, θr=1.5, β=0.5, and ξ=1.
Fig.14. Velocity profile for different values of Dc for N=1, Le=1,
Ds=0.3, Dc=0.3, a=0.5, θr=1.5, β=0.5.
1 1
0.9
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Dc = 0.1
Dc = 0.3
Dc = 0.5
Dc = 1
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
ξ = 0.5
ξ = 1
ξ = 1.5
0 0.5 1 1.5 2 2.5 3 3.5 4
η
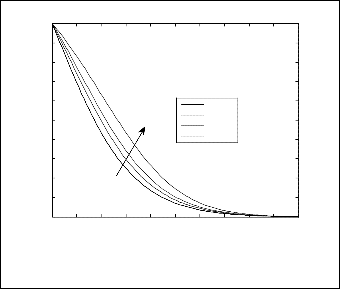
Fig.12. Temperature profile for different values of Dc for N=1, Le=1,
Ds=0.3, a=0.5, θr=1.5, β=0.5, and ξ=1.
Fig.15. Temperature profile for different values of Dc for N=1,
Le=1, Ds=0.3, Dc=0.3, a=0.5, θr=1.5, β=0.5.
1 1
0.9
0.9
0.8
0.8
0.7
0.6
0.5
0.4
Dc = 0.1
Dc = 0.3
Dc = 0.5
Dc = 1
0.7
0.6
0.5
0.4
ξ = 0.5
ξ = 1
ξ = 1.5
0.3
0.2
0.1
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
η
0.3
0.2
0.1
0
0 0.5 1 1.5 2 2.5 3 3.5 4
η
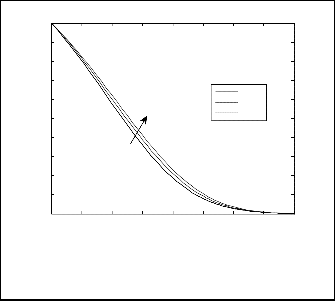
Fig.13. Concentration profile for different values of Dc for N=1,
Le=1, Ds=0.3, a=0.5, θr=1.5, β=0.5, and ξ=1.
Fig.16. Concentration profile for different values of Dc for N=1,
Le=1, Ds=0.3, Dc=0.3, a=0.5, θr=1.5, β=0.5.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 91
ISSN 2229-5518
θ = 1.5
r
θ = 2
r
0.55 θ = 3
r
0.94
0.92
β = 1
β = 2
β = 3
0.9
0.5
0.88
0.45
0.86
0.84
0.4
0 2 4 6 8 10
0.82
0 2 4 6 8 10
ξ
ξ
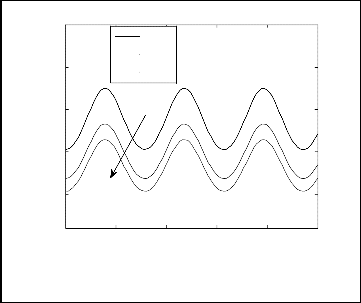
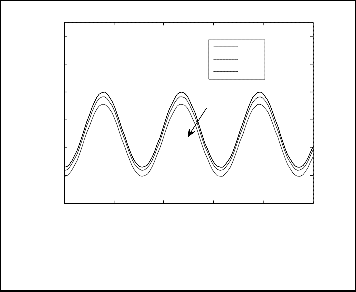
Fig.17. Axial distribution of the Nusselt number for different values of
variable viscosity for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5, ξ=1, β=0.5.
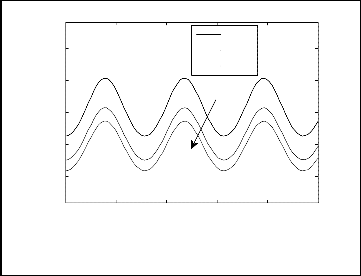
Fig.20. Axial distribution of the Sherwood number for different values of variable thermal conductivity for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5,
ξ=1, θr=1.5.
0.7
0.65
θ = 1.5
r
θ = 2
r
θ = 3
r
1
0.9
Ds = 0.1
Ds = 0.3
Ds = 0.5
0.6
0.8
0.55
0.7
0.5
0.6
0 2 4 6 8 10
ξ
0.5
0 1 2 3 4 5 6 7 8 9 10
ξ
Fig.18. Axial distribution of the Sherwood number for different values of
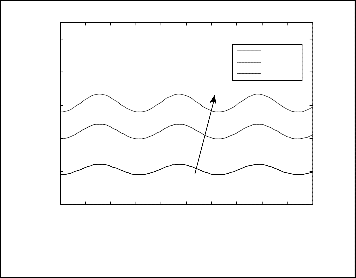
variable viscosity for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5, ξ=1, β=0.5.
Fig.21. Axial distribution of the Nusselt number for different values of
Ds for N=1, Le=1, β=0.5, Dc=0.3, a=0.5, ξ=1, θr=1.5.
1
0.9
0.8
0.7
β = 1
β = 2
β = 3
0.94
0.92
0.9
0.88
Ds = 0.1
Ds = 0.3
Ds = 0.5
0.6
0.86
0.5
0.84
0.4
0.82
0.3
0 1 2 3 4 5 6 7 8 9 10
ξ
0.8
0 2 4 6 8 10
ξ
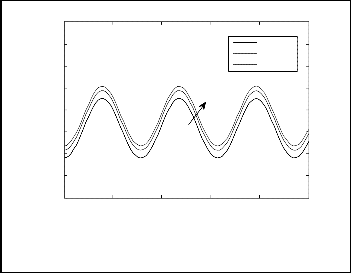
Fig.19. Axial distribution of the Nusselt number for different values of variable thermal conductivity for N=1, Le=1, Ds=0.3, Dc=0.3, a=0.5,
ξ=1, θr=1.5.
Fig.22. Axial distribution of the Sherwood number for different values
of Ds for N=1, Le=1, β=0.5, Dc=0.3, a=0.5, ξ=1, θr=1.5.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 92
ISSN 2229-5518
0.82
0.8
0.78
0.76
0.74
Dc = 0.1
Dc = 0.3
Dc = 0.5
0.94
0.92
0.9
0.88
a = 0.0
a = 0.2
a = 0.4
a = 0.5
0.72
0.86
0.7
0.68
0.66
0.84
0.82
0.64
0 2 4 6 8 10
ξ
0.8
0 2 4 6 8 10
ξ
Fig.23. Axial distribution of the Nusselt number for different values of Dc
for N=1, Le=1, β=0.5, Ds=0.3, a=0.5, ξ=1, θr=1.5.
Fig.26. Axial distribution of the Sherwood number for different values of
‘a’ for N=1, Le=1, β=0.5, Ds, =0.3, Dc=0.3, a=0.5, ξ=1, θr=1.5.
1.1
Dc = 0.1
Dc = 0.3
Dc = 0.5
1
0.9
0.8
0.7
0.6
0 1 2 3 4 5 6 7 8 9 10
ξ
Fig.24. Axial distribution of the Sherwood number for different values of Dc
for N=1, Le=1, β=0.5, Ds=0.3, a=0.5, ξ=1, θr=1.5.
0.8
0.78
0.76
a = 0.0
a = 0.2
a = 0.4
a = 0.5
0.74
0.72
0.7
0.68
0.66
0 2 4 6 8 10
ξ
Fig.25. Axial distribution of the Nusselt number for different values of ‘a’ for
N=1, Le=1, β=0.5, Ds, =0.3, Dc=0.3, a=0.5, ξ=1, θr=1.5.
IJSER © 2014 http://www.ijser.org