International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014
ISSN 2229-5518
1036
Determination of True Residual Stress within In- situ Sampled Clay
A.A Owayo1, C.Y Ou2
Abstract— The objective of this study is to establish a reliable way to determine the residual stress in clay. During saturation in triaxial test, using residual stress as back pressure as opposed to the traditional saturation methods leads to better sample quali- ty. In this research the residual stress within the sample is measured and compared against the one that can be predicted wit h the help of the equation proposed by Skempton in 1954 based on the account of change in total stress during sampling. The re- sults do not exhibit any recognizable trend, in fact sometimes the prediction is quite good while the rest of the time not good. Thus in the absence of a perfect sample, the use of Skempton’s equation is more reliable.
Index Terms—clay, perfect sample, residual stress, sampling, saturation, triaxial test, true residual stress
—————————— ——————————
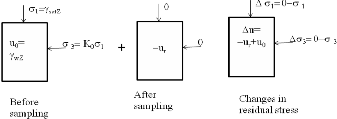
During triaxial testing we require a sample with as minimal disturbance as possible. The in-situ conditions needs to be pre- served as best as possible. Practically speaking is almost im- possible to have a perfect sample (without disturb- ance).Inevitable disturbance may be encountered during sam- ple extrusion, trimming etc. Presence of foreign material like silt or sand may also lead to pore water pressure dissipation thus the measured residual stress may not necessarily the true value. Tube samples of Taipei silty clay sampled from within the environs of Taipei 101 were used. Taipei Silty clay normally has hydrostatic water levels to be 2 metres below the surface. Skempton (1954) proposed an equation that may be used to estimate residual effective stress within a sample based on the account of total stress changes.
Residual effective stress also called the initial mean effective stress,stored effective stress or effective stress after sampling is the effective stress remaining in the soil sample after sampling, handling ad storage(Skempton& Sowa 1963, Ladd and lambe 1964, Hight 2003). This is a concept rooted in perfect sampling concept(Lambe and Ladd 1964) where there would be no disturbance except that from stress relief.The
difference between sampling effective stress and the residual
effective stress is caused by disturbance rather than stress relief.This implies sthat the residual stress can be a qulitative measure of sample disturbance (Finno et al, 2006).The sample swelling thus disturbance during saturation, can be minimized by applying an effective stress equal to the measured residual stress before adding water to the specimen, Finno et al., 2006. This implies that the sample quality may be improved further if the correct or ‘true’ residual stress is used.This informed by the fact that due to storage,snd sample handling the sample may undergoe inevitable pore pressure dissipation and hence the measured residual stress may not necessarily be the ‘true’ value. The measured residual stress is applied as back pressure during saturation. In the conventional saturation process a very small back pressure (0~10kPa) is normally used.The basic soil properties are as summarized below in table 1.
IJSER © 2014
International Journal of Scientific & Engineering Research Volume 5, Issue 5, May-2014
ISSN 2229-5518
1037
TABLE 1
![]()
![]()
USCS Properties wn (%) 33.0~40.0
![]()
LL(%) 38.0 ~38.5
PL(%) 26.0~26.3
![]()
PI(%) 12.0~12.2
SL(%) 7.5
![]()
t (kN/m3) 18.0~20.0
Gs 2.7
e0 0.98
![]()
During sampling the soil undergoes unloading thus stress release. This means that after sampling the underlying layers now carry less load than before this situation is similar to axial
extension in the triaxial test.
during sampling (Holtz &Kovacs 1999).
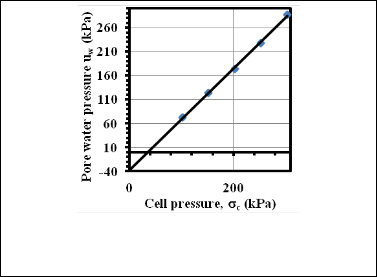
The effective stress, p’r , was evaluated prior to saturation through the response of excess pore-water pressure as isotropic stress increaments applied with drainage lines closed (Lambe and ladd 1963).The total confining stress, cwas increased in 50kPa from 100kPa to 300kPa and reduced in
100kPa from300kPa to 100kpa.In each load increament step the pore water, u, was allowed to equillibrate within 30-60 min. The same procedure was followed in reducing
c.Expected response of u to c is as shown in Fig. 2. Linear
regression applied to this data, the matric suction within the sample can be taken as th e value of u at c=0. Following the general concept of effective stress,the residual effective stress,
p’r may be defined:
p’r=-u r (3)
3 1 3
u
A( )
u0 u p'
r
The equation (1) as proposed by Skempton in 1954 can be used to estimate the changes due to stress relief. k0 for saturated soil is taken as 0.5, B=1 and A=2/3 for axial extension synonymous to unloading
————————————————
![]()
2 is currently a senior professor at the department of Civil and Construction engineering at National Taiwan University of Science and Technology Tai-
pei Taiwan ROC,+886227375578. E-mail: ou@mail.ntust.edu.tw
IJSER © 2014
International Journal of Scientific & Engineering Research Volume 5, Issue 5, May-2014
ISSN 2229-5518
1038
TABLE 2
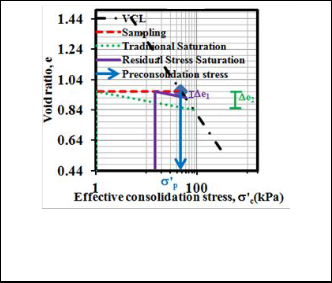
When the consolidation stress is higher than the in-situ pre- consolidation stress the soil sample is at the virgin consoli- dation line (VCL), where it is normally consolidated. Pres- ence of foreign materials e.g silt, organic matter may lead to![]()
Test Sample
depth,m
Water
content,
w (%)
Measured
residual
stress
(kPa)
Calculated
residual
stress
(kPa) eqn
2
Effective
vertical
stress
(kPa)
residual stress dissipation. Some minimal disturbance may also be caused to the sample during trimming. Thus the measured residual stress may not be the actual, correct or the ‘true’ residual stress immediately after sampling. Due to this, the results from equation 2 are considered more
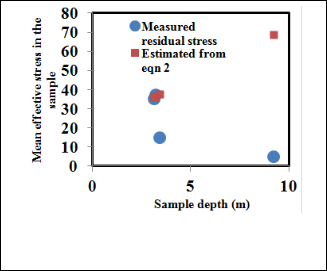
Sample 1 3.23 36.3 37.05 36.40 46.26![]()
Sample 2 3.43 35.74 15.00 37.61 47.92![]()
Sample 3 9.23 33.07 5.00 68.60 96.55![]()
Sample 4 3.12 40.01 35.00 35.94 45.34
reliable.
![]()
Test e0 e e2/e e1 e1/e0![]()
Sample1 0.98 0.03 0.03 0.24 0.24
Sample 2 0.96 0.05 0.05 0.11 0.11![]()
Sample 3 0.89 0.08 0.09 0.12 0.13![]()
Sample 4 1.11 0.04 0.04 0.16 0.14
![]()
Sample quality Volume change
e/e 0![]()
Very Good <0.04
Good to Fair 0.04~0.07![]()
Fair to Poor 0.07~0.14
![]()
Very Poor >0.14
IJSER © 2014
International Journal of Scientific & Engineering Research Volume 5, Issue 5, May-2014
ISSN 2229-5518
1039
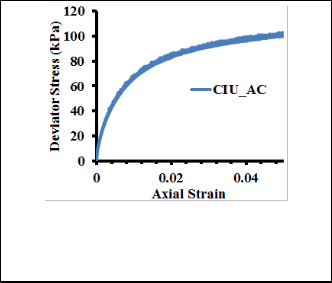
during saturation in the triaxial test the sample quality is quite improved. Since the sample may often than not be disturbed even if slightly so that the measured residual stress is not the expected true residual stress, hence in the absence of a perfect sample the prediction from equation 2 would be more
reliable.
Comparison between the measured residual stress and the estimation from equation 2 do not exhibit any recognizable trend, in fact sometimes the prediction is quite good while at other times it is not good. This may be explained in the light of inevitable disturbance of the sample probably due to presence of foreign material slight disturbance during trimming etc. Thus in the absence of a perfect sample, the use of Skempton’s equation to predict the residual stress is more reliable.
When the measured residual stress is used the volumetric changes are far much less as compared to when traditional saturation process is employed. The classification of sample quality ranges from ‘Fair to Poor’ to Very good when residual stress is used as back pressure. When conventional saturation i.e when 1kPa is used as back pressure during saturation the classification is from ‘Very Poor’ to ‘Fair to Poor’. It is ex- pected thus, that if the ‘true’ residual stress estimated from equation 2 is used all the samples would fall within the ‘Very
Good’ quality classification.
REFERENCES
[1] Wanjei Cho, Terence P. Holman, Young –Hoon Jung, Richard J. Finno,
“Effects of swelling during saturation in Triaxial Test in Clay,” Ge- otechnical testing Journal v30 No. 5, pp. 4, 2007.
[2] A.W.Skempton, “Pore pressure coefficients A and B,”
[3] Fu-Chen Teng, Chang-Yu Ou, “Application of suction control System in the Method of specimen Saturation in Triaxial tests,” Geotechnical
testing Journal v34 No.6 (2011) pp. 2, 2011.
[4] Robert D. Holtz and William D Kovacs, An introduction to Geotechnical engineering.Taylor, Francis: Carlifornia States Universityl, pp. 125-138,
1978.
[5] Braja M. Das, Advanced Soil Mechanics. N.M. Newmark, W. J. Hall.: Prentice hall, pp. 691-693, 1981.
[6] Standard Test Method for Consolidated Undrained Triaxial Com-
pression Test forCohesive Soils ASTM D4767 – 11.
When measured residual stress is used as back pressure
IJSER © 2014