International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 302

ISSN 2229-5518

Determination of Monthly Tilt Angle and

Solar Energy Potentials of Jos

Zwalnan S. Johnson1, Kamtu M. Peter2, Borok I. Maren3

Abstract- Detailed information about the availability and nature of solar radiation in a particular location is essential for the optimum design of solar energy conversion system. This paper determines by empirical analysis the potentials for the utilization of solar radiation for generation of solar energy in Jos Nigeria (latitude 9.90 N and longitude 8.90 W ) and the optimization of the monthly average daily solar energy received on a tilted surface and. The methodology used to achieve this involved gathering sufficient

monthly daily mean solar radiation data of Jos on horizontal surface for 11 years (2000-2011). The data which was obtained from the Federal Airport Authority of Nigeria Jos, was analysed to obtain a monthly mean daily representative solar radiation data of Jos. The monthly average daily representative data was used as input into a simulation programme written in MATHLAB programming language to predict the beam and diffused components of the monthly average daily total solar radiation on a horizontal surface. The programme was also use to predicts the monthly tilt angle required to capture the maximum monthly average daily available solar radiation. The results of simulation shows that Jos has an annual total , beam and diffuse monthly average daily solar energy of 21.7MJ/m2 , 15.0MJ/m2 ,and 6.7MJ/m2 respectively on a horizontal surface., The results also reveals that solar energy conversion surface installed horizontally (0o) receives maximum energy for the months of January February , March , October, November and December and surface installed at 10o, 16.5o 22 o 19o 10o and 5o receives maximum solar energy for the months of April, May, June , July August and September respectively. This analysis reveals very great potential for electricity generation and domestic hot water heating even if conversion system is to function at 15% efficiency.

Keyword: Environmental security, solar radiation, and Green House Gases (GHG).

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 303

ISSN 2229-5518

INTRODUCTION

The development of a sustainable, long-term solution to meeting the world’s energy needs is a defining issue of our time. Energy is directly linked with the key global challenges that the world faces today; poverty alleviation, climate change, and global environmental and food security. There is a strong consensus among scientists who study climate that the environmental problems now observed is caused by human activity targeted to meeting our energy demand, especially the combustion of fossil fuels. When oil, gas, or coal are burned to propel cars, generate electricity or provide heat, the products of the combustion are mainly the green house gases. Thus, our conventional energy systems are in large measure responsible for this impending environmental problem [1].
With the rapid depletion of fossil fuel reserves, it is also feared that the world will soon run out of its energy resources. Under these circumstances it is highly desirable that alternate energy resources should be utilized with maximum conversion efficiency to cope with the ever increasing energy demand. Among the non-conventional energy resources, solar energy is one of the most prospective options to solve our energy and environmental problems. Detailed information about the availability of solar radiation is essential for the optimum design and study of solar energy conversion system. [2]
This work is aim at analyzing and predicting the monthly values of solar radiation received on horizontal and tilted surface in Jos, a town located near the center of Nigeria on a latitude of 9.9o North and longitude of 8.9o west and with an area of
8600 km² and bounded by 300-600 meter escarpments
around much of its circumference. Because most stations in Nigeria do not have instrument to measure the beam and diffuse component of the global radiation, models which predict the distribution of monthly global solar radiation into beam and diffuse components as developed in Duffie and Beckman
2006 [3] will be used to predict the monthly
distribution of the global solar radiation in Jos through simulation programme written in MATHLAB programming language. [4]

MATERIALS AND METHODS.

Solar radiation often seems to be highly random and irregular. However, long-term statistical analysis indicates that the solar radiation of a particular location are predictable to some degree by formulating a representative data which can characterized the mean-value behavior of any location over a long period [5]. Based on this method, the monthly average daily values of solar radiations of Jos for eleven years (11) obtained from Federal Airport Authority of Nigerian (FAAN) Jos were statistically analyzed to obtain a mean representative data which can characterized the monthly average daily value behavior of solar radiation of Jos. The mean representative data which characterized the monthly average daily value behavior of solar radiation of Jos was used as input into a simulation program written in Mathlab programming language [4] to predict the value of beam and diffuse radiation on both horizontal and tilted surfaces. The program was equally used to study the effect of the tilt angle on the amount of solar radiation incident on a collecting surface and to determine the monthly optimum tilt angle necessary to receive maximum amount of solar radiation on a surface. The following Solar variables prediction models were used for the simulation program:

Declination: The declination is the angular position of the sun’s ray north or south of the equator. It is the angle between a line extending from the sun to the centre of the earth and the projection of the line upon the earth’s equatorial plane. Its value in degrees is given by Cooper’s equation as:

𝛿 = �23.45𝑠𝑖𝑛 �2𝜋 𝑛+284�� [6]. (1)

365

Where n is the recommended average day for the
month as indicated in table 1 used for the simulation. Where n is the recommended average day for the month as indicated in table 1 used for the simulation.

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 304

ISSN 2229-5518

Table 1 Recommended average days for the month and values of n by month.

Radiation on Tilted Surface: For the purposes of solar process design and performance calculations, it is necessary to know the radiation on the plane of the collector from measurements or estimates of radiation on horizontal surfaces. However, the most commonly available data are that of daily and monthly average radiation on horizontal surfaces, whereas the need is for beam and diffuse radiation on horizontal and tilted surfaces. To compute monthly average radiation in the plane of a tilted surface, the Liu and Jordan’s [8] isotropic model is used as:

𝑇 = 𝐻 �1 −

𝐻�𝑑

� 𝑅�
+ 𝐻�
�1+𝑐𝑜𝑠𝛽
� + 𝐻�𝜌𝑔 �

1−𝑐𝑜𝑠𝛽

� (5)
𝐻� �

𝐻� 𝑏

𝑑 2 2

Liu and Jordan suggested the geometric factor R� b can
be estimated by assuming that it has value which

would be obtained if there were no atmosphere. For surfaces that are sloped toward the equator in the northern hemisphere that is surfaces with surface azimuth angle equal to zero.
Source: [2]

cos(∅+𝛽) cos 𝛿 sin 𝜔𝑠 1+(

)𝜔 1 sin(∅+𝛽) sin 𝛿

𝑎 =

180 𝑠

cos ∅ cos 𝛿 sin 𝜔 + 𝜋 𝜔 sin ∅ sin 𝛿

The Sunset Hour Angle: The sun set hour angle

𝑠 180 𝑠

−1

on an inclined surface is the solar hour angle
Where: 𝜔𝑠1 = 𝑚𝑖𝑛 � cos

(− tan ∅ tan 𝛿 )

� (7)
corresponding to the time when the sun sets. It is an indication of how long the sun is up during the day. It is given by the equation:
𝑐𝑜𝑠𝜔𝑠 = −𝑡𝑎𝑛∅𝑡𝑎𝑛𝛿 (2)

Extraterrestrial Radiation and Clearness Index:

Solar radiation outside the earth’s atmosphere is called extraterrestrial radiation. The monthly average daily extraterrestrial radiation on horizontal surface for latitude in the range of -60 to +60 degree can also
be predicted the equation:

cos−1(− tan(∅+𝛽) tan 𝛿)

Where “min” means the smaller of the two in the
bracket.
The total radiation, H, are obtained from radiation
data, but the distribution of this total radiation term
into the diffuse and beam components must be
estimated based on the sun angle and the clearness of the sky according to the Collares-Pereira and Rable correlation [9]

𝐻𝑑 = 0.775 + 0.00606(𝜔 − 90) − [0.505 +

𝐻 𝑠

𝑂 =

86400𝐺𝑠𝑐 �1 + 0.033𝑐𝑜𝑠 �360𝑛�� (𝑐𝑜𝑠∅ cos 𝛿 𝑠𝑖𝑛𝜔 +

0.00455(𝜔𝑠 − 90)]𝐶𝑜𝑠(115𝐾𝑇 − 103) . (8)
And the beam component of the total radiation on a

𝜋 365

𝑠 horizontal surface can thus be calculated as:

𝜔𝑠 sin ∅ sin 𝛿 [7] (3)
Before reaching the surface of the earth, radiation
from the sun is attenuated by the atmosphere and the
clouds. The effect expressed in a dimensionless index called the clearness index. Thus the monthly average
𝐻� � �

𝑏 = 𝐻 − 𝐻𝑑 (9)

RESULTS AND DISCUSSION

clearness index 𝐾�
is defined as: The ratio of the
monthly average daily radiation on a horizontal surface to the monthly average daily extraterrestrial radiation. Written as::

Solar Energy Potential of Jos.

Figure (1) shows the monthly average daily solar representative data of Jos Nigeria (latitude 9.9oN and longitude 8.9 West) obtained from the long term
𝐾�

𝐻�

analysis of solar data from 2001 -2011 (Appendix A)

𝑇 = 𝐻�

(4)
obtained from the Federal Airport Authority of Nigeria Jos using simulation programme written in Mathlab.

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 305

ISSN 2229-5518

Optimisation of Monthly Tilt angle 𝜷

40 H

35 o

25 H

20 b

15 d

Figure 2 shows the effect of varying the tilt angle on the monthly average daily solar radiation for the months of January to March. The figure shows that as the tilt angle increases from zero to 60 degrees, the amount of solar radiation received on the tilted surface decreases. This result implies that for optimum system performance of solar energy conversion system, solar system installed in this location (Jos) should be installed horizontally for the months of January to March.

0 2.8

2.6

x 10

Jan Feb March

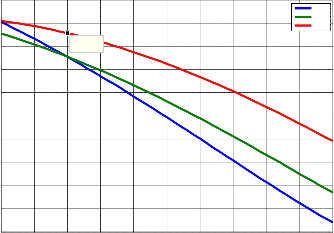
Figure (1): Monthly average daily solar radiation analysis of Jos
Ho, H, Hb and Hd in figure (1) represent the monthly average daily extraterrestrial, total, beam and diffuse solar radiation on horizontal surface respectively. Figure (1) shows that Jos has an annual monthly average daily total solar radiation, beam and diffuse radiation of 21.7MJ/m2 15.0MJ/m2 and 6.7MJ/m2 respectively. The analysis as presented in figure (1) also reveals that this location receives higher amount of solar radiation from the months of January to April. This could be explained from the fact that this period of time in the said location corresponds to the dry season and the sky is cover with lesser amount of cloud and therefore higher amount of solar radiation

2.4

2.2

1.8

1.6

1.4

1.2

0.8

X: 10

Y: 2.513e+007

0 5 10 15 20 25 30 35 40 45 50

Surface tilt angle (degrees)

Figure (2) : Effect of tilt angle on the amount of
is allowed to reach the earth surface. The figure also shows that the amount of solar energy received decreased from the months of May to August and increased again from September to November. The worst solar radiation was received in August because this period correspond to the Peak of rainfall in Jos and most solar radiation is absorbed in the sky by the heavy cloud cover. The figure reveals a monthly average daily solar potential of more than 3.47MJ/m2 per day from the months of January to April and from the months of September to December even for solar conversion technology functioning at low as 15% efficiency only. This analysis reveals very good solar energy potential for both total and beam solar energy conversion system.
solar radiation for the months of January, February
and March.
Figure (3) is the result of the optimization of the tilt angle for the months of April, May and June . The figure indicates an optimum tilt angle of 10o, 18o and
23o for the months of April, May and June respectively. By implication, this means that solar energy conversion designed based on monthly average daily solar and weather data should be designed to track the solar radiation at the above mentioned angles for the months of April, May and June for optimum system
performance.

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 306

ISSN 2229-5518

2.25

2.2

2.15

2.1

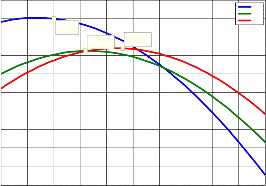
x 10

X: 10

Y: 2.2e+007

X: 16

Y: 2.112e+007

X: 23

Y: 2.119e+007

April May June

2.4

2.2

1.8

x 10

Oct Nov. Dec.

2.05

1.6

1.95

1.4

1.9

1.2

1.85

1.8

1.75

0 5 10 15 20 25 30 35 40 45 50

Surface tilt angle (degrees)

0.8

0.6

Figure (3) : Effect of tilt angle on the amount of solar
radiation for the months of April, May and June.
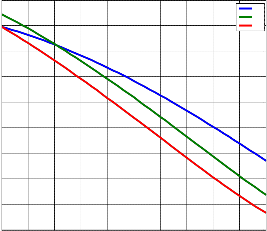
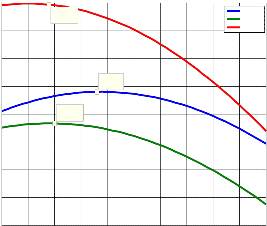
Figure (4) shows that solar radiation received per square meter in the months of July, August and September is optimized at tilt angle of 18o, 10o and 0o to 9o respectively. Figure (4) and figure (5) indicates that solar energy conversion system receives optimum amount of solar radiation per square meter for the months of September, October, November and December if system is installed horizontally

x 10

0 5 10 15 20 25 30 35 40 45 50

Surface tilt angle (degrees)

Figure (5) : Effect of tilt angle on the amount of solar radiation for the months of October, November and December

CONCLUSION

The analysis in this paper reveals that Jos has an estimated annual monthly average global radiation of
21MJ/m2 on horizontal surface. The monthly value of the amount global solar radiation received on a surface varies as the tilt angle varies. The value of the

2.2

2.1

1.9

1.8

1.7

1.6

X: 9

Y: 2.194e+007

X: 10

Y: 1.766e+007

X: 18

Y: 1.88e+007

July August September

optimum tilt angle lies between 0o to 23o from January to December which implies that solar system installed at tilt angle greater than 23o will perform significantly below optimum performance. The estimated monthly values of global radiation with a minimum value of
17.6MJ/m2 in August and maximum of 26.6MJ/m2 in March presented very good solar potentials capable of meeting residential hot water and lighting needs. This will reduce over dependent on fossil fuel which is the primary contributor of green house gases into the atmosphere.

1.5

1.4

0 5 10 15 20 25 30 35 40 45 50

Surface tilt angle (degrees)

ACKNOWLEDGMENT

The authors wish to thank the management of the
Figure (4) : Effect of tilt angle on the amount of solar radiation for the months of July, August and September
Federal Airport Authority of Nigeria Jos for providing the Authors with the monthly average daily solar radiation data of Jos for the period of 2001
-2010.

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 307

ISSN 2229-5518

REFERENCES

	[1]	Intergovernmental Panel on Climate Change (IPCC): IPCC Third Assessment Report—Climate
		Change .Summary for Policy Makers. Geneva, Switzerland. 2001.
	[2]	Alternative Energy Tutorials. Home of Alternative and Renewable energy. 2012 Retreived January 20,
		2012 from http://www.alternative-energytutorials. com/.
	[3]	Duffie JA, Beckman WA. Solar engineering of thermal processes, 2nd ed, Toronto: John Wiley & Sons. 1991.
	[4]	Palm WJ. Introduction to MATLAB® for Engineers, 3rd Edition, New York: Graw-Hill. 2011
	[5]	Lin Q. Analysis modelling and optimum design of solar domestic hot water system. PhD thesis, University
		of Wisconsin. 1998. Retrieved from http://sel.me.wisc.edu/theses.
	[6]	Bob T. Performance of a solar hot water system. 2007. Retrieved from 13th march 2011 University of
		Wisconsin- Madison Digital Dissertation..
	[7]	Anna H. Conceptual design of a solar-thermal heating system with seasonal Storage for a Vashon
		greenhouse. Master’s thesis, University of Washington. 2006. Retrieved from http:
		faculty.washington.edu/malte/pubs/Anna_Thesis.p df.
.	[8]	Liu BY, Jordon RC. Daily insolation on surfaces tilted toward the equator. ASHRAE Journal 1962;53:3-10.
	[9]	Hay JE, Davies JA. Calculation of the solar radiation incident on an inclined surface. Proceedings of the
		First Canadian Solar Radiation Data, Workshop. 1980. p.59–72

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 308

ISSN 2229-5518

APPENDICES

APPENDIX A

MATLAB PROGRAMME CODES
clear all
month=[1 2 3 4 5 6 7 8 9 10 11 12]';
Beta=9.8;% tilt angle. Pi=22/7;
Lat=9.8;
P=Pi/180;
Gsc=1367; % W/m sqr % solar constant.
M_Average=[17;47;75;105;135;162;198;228;258;288;318;344];
n_average=M_Average(:,1);
decl=23.45*sin(2*pi*(n_average+284)/365)
plot(month,decl)

% sun set hour angle and extraterestrial radiation estimation

OmegaS=(acos(-tan(Lat*Pi/180)*tan(decl*Pi/180)))*180/Pi daylighthour=(2/15)*(acos(-tan(Lat*pi/180)*tan(decl*pi/180))*180/pi) A1=86400*Gsc/Pi;
A2=(1+0.033*cos(360*n_average*P/365)); A3=cos(Lat*P).*cos(decl*P).*sin(P*OmegaS)+(OmegaS*sin(P*Lat).*sin(P*decl)/180); Ho_bar=A1.*A2.*A3;

% measured total radiation per meter square on horizontal surface

H=[20978541.8 21421570.9 21564654.5 20734396.4 18834381.8 17936738.2 14966836.4 13757334.5 11773832.7 11584145.5
14583829.1 16904389.1]'

% monthly average daily clearness index (KT) KT=H./Ho_bar;

% estimation of ratio of monthly average daily diffuse to total rad.

for i=1:12

Omega1=(acos(-tan(Lat*P)*tan(DC*P)))*180/Pi
Omega2=(acos(-tan((Lat-Beta)*P)*tan(DC*P)))*180/Pi
OmegaS1=min(Omega1,Omega2)

end

for i=1:12

Rb1=(cos((Lat-Beta)*P)*cos(decl*P).*sin(OmegaS1*P)+(Pi/180)*OmegaS1(i)*(sin((Lat-Beta)*P)*sin(decl*P))); Rb2=(cos(Lat*P)'*cos(decl*P).*sin(OmegaS1*P)+((Pi/180)*OmegaS1(i)*(sin(Lat*P)'*sin(decl*P)))); R_bar=(Rb1./Rb2)

end

kk=cos(115.*KT-103)*pi/180
HdH=0.775+0.00606*(OmegaS1-90)-(0.505+0.00455*(OmegaS1-90)).*kk
Hd=H.*HdH Hb=H-Hd

% tilted rad. rho=0.2;

HT1==((1-HdH).*R_bar.*H)+(((1+cos(Beta*P))/2).*Hd)+(((1-cos(Beta*P))/2).*H*rho)

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 309

ISSN 2229-5518

%APPENDIX B

%TILT ANGLE OPTIMISATION

Gsc=1367
LAT=9.92

%recomended days of the months

nr=[17 47 75 105 135 162 198 228 258 288 318 344]'
Hr=[26.0 25.0 26.2 24.1 20.5 20.1 18.1 17.5 19.5 21.9 22.9 21.7]'*1e6
n1=[17 47 75 105 135 162 198 228 258 288 318 344]' %Average day of the year for i=1:length(n1)
beta=(0:1:60)'
P=pi/180 %factor for the conversion from radian to degree. DLTA=23.45*sin(2*pi*((n1(i)+284)/365)) %formula for monthly declination w_s=(acos(-tan(LAT*P).*tan(DLTA*P)))*1/P %monthly sunset angle
w_sb=(acos(-tan((LAT+beta)*P).*tan(DLTA*P)))*1/P
w_s1=min(w_s,w_sb) %minimum of line 8 and 9. A1=86400*Gsc/pi; A2=(1+0.033*cos(360*n1(i)*P/365));
A3=cos(LAT*P).*cos(DLTA*P).*sin(P*w_s)+(pi.*w_s*sin(P*LAT).*sin(P*DLTA)/180); Ho=A1.*A2.*A3 %annual average extrateresterial solar radiation of location H=[21.91]*1e6 %annual average solar radiation of location
KT= H./Ho
Hd1=0.775+0.00606*(w_s-90) Hd2=(0.505+0.0045*(w_s-90)).*cos((115*KT-103)*P) Hd=(Hd1-Hd2).*H
Hb=H-Hd Rb1=cos((LAT+beta)*P).*cos(DLTA*P).*sin(w_s1*P) Rb2=(pi/180)*w_s1.*sin((LAT+beta)*P)*sin(DLTA*P) Rb3=cos(LAT*P)*cos(DLTA*P)*sin(w_s*P) Rb4=(pi/180)*w_s*sin(LAT*P)*sin(DLTA*P) Rb=(Rb1+Rb2)/(Rb3+Rb4)
HT1=(H.*(1-(Hd./H)).*Rb+Hd.*(1+cos(P.*beta))/2)'
HT2=(H.*0.2.*(1-cos(P*beta))/2)' HT=(HT1+HT2) plot(beta,HT,'r','linewidth',4)
xlabel('Surface tilt angle (degrees)','fontsize',12)
ylabel('solar radiation on tilted surface (J/sq.m.day)','fontsize',12)
grid legend('n=Jan','n=Feb','n=marc','n=April','n=May','n=June','n=july','n=4.Aug','n=Sept','n=Oct','n=Nov','n=dec','fontsize',1
8)

end

hold off