International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015 1620

ISSN 2229-5518

Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges

Marwah Almasri and Khaled Elleithy

Abstract—In W SNs, the most critical issue is energy consumption as sensor nodes have limited resources. The sensors collect data from the environment where they can fail due to variations in pressure, temperature, and electromagnetic noise. All these can result in misleading readings and measurements where a lot of energy is consumed. Therefore, data fusion is used to overcome these challenges as it assures the accuracy and the efficiency of gathered data, and eliminates data redundancy which results in saving power, thus improving the overall network performance. This paper provides a survey of research related to the data fusion domain to explore many aspects of data fusion in terms of architecture, taxonomy, and techniques and methods. It also evaluates and compares these techniques as it investigates the advantages and the drawbacks of each, and emphasizes the applicability of these techniques in the W SN domain. Finally, it presents the data fusion challenges in W SNs.

Index Terms—W ireless Sensor Networks (W SNs), Data Fusion, Data Fusion Architecture, Data Fusion Techniques, Data Fusion

Taxonomy, Data Fusion Challenges.

1 INTRODUCTION

——————————  ——————————
he Wireless Sensor Network (WSN) is a network that is composed of a large number of sensors. These sensors are used to sense and observe the surrounding environment. Subsequently, measurements and readings are collected in order to be sent to the sink node. WSNs have gained a central attention in latest research trends. However, many issues should be considered as these sensors have a limited computa-
tional capability as well as limited energy.
In WSN, sometimes sensors fail to collect accurate data
from the environment due to pressure and temperature. In
other cases, this failure can be attributed to electromagnetic noise or radiation. Therefore, all readings and measurement would be inaccurate and inefficient. In order to overcome these problems, data fusion which is a technique to combine data from several sources to be more accurate and complete, is used. Data fusion is applied in centralized systems as well as in distributed systems [1]. It extends the lifetime of the net- work, which is a challenging research aspect of WSNs [1]. Da- ta fusion can eliminate redundant data and thus save energy, which results in an improved network performance [2].
Data fusion has been used in many detection applications such as robotics [3]. Recently, new applications such as Denial of Service (DoS) detection deploy the data fusion concept suc- cessfully [4]. Another example is intrusion detection [5]. In WSNs, data fusion is applied in order to enhance the estima- tions of sensor nodes’ locations [6].

————————————————

• Marwah Almasri is currently pursuing PhD degree program in computer science and engineering at University of Bridgeport, Bridgeport, CT 06604, USA. E-Mail: maalmasr@my.bridgeport.edu

• Prof. Khaled Elleithy is the Associate Dean for Graduate Studies in the

School of Engineering at the University of Bridgeport, Bridgeport, CT

06604, USA. E-Mail: elleithy@bridgeport.edu.

In relation to the importance of data fusion especially in WSNs, this paper highlights the different architectures of data fusion and provides detailed information about various data fusion taxonomy where all existing taxonomy are combined to give the reader a wider overview. It also presents many tech- niques that have been applied in WSNs and sensor based sys- tems in general. Our goal is to analyze each technique and evaluate the advantages and the disadvantages of each in or- der to comprehend the best usability of these techniques in different applications especially in WSNs. In addition, this survey indicates the challenges of data fusion in WSNs.
This paper is organized as follows: section 2, provides the
data fusion architectures. Section 3, presents several data fu-
sion taxonomies. Section 4, discusses in detail different data
fusion techniques. Section 5, evaluates these techniques and
concludes the advantages and the limitations of each. It also highlights the best and suitable techniques to be applied in WSNs. Section 6, states the data fusion challenges in WSNs. Finally, section 7, concludes our final remarks of the data fu- sion domain and its applicability in WSNs.

2 DATA FUSION ARCHITECTURE

This section presents the different data fusion architectures applied in WSNs. There are centralized, decentralized, and hierarchical architecture. Each one has its advantages and dis- advantages as discussed in the following sub-sections.

2.1 Centralized Architecture

Centralized architecture is the traditional and the simplest architecture in WSNs. In this architecture, there is one central node which is called central processor fusion that receives the sensed data from all other nodes. The central node is also re- sponsible for fusing all reports gathered by the sensing nodes [7]. The advantage of the centralized architecture is that it is simple and optimal. Another advantage is that faulty reports can easily be detected. On the other hand, this architecture requires more resources for data processing as it needs higher

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1621

ISSN 2229-5518

bandwidth for transmitting data from all sensing nodes to the central processor fusion [8]. Fig. 1, shows the centralized archi- tecture of WSNs.

Fig. 1. The Centralized data fusion architecture.

2.2 Decentralized Architecture

Unlike the centralized architecture, the decentralized architec- ture has no single central node. However, data fusion is im- plemented locally at each node in the network based on the observations from neighbor nodes. The advantages of this ar- chitecture are as follows: the support of any dynamic changes in the network, scalability, and tolerance [7]. This architecture has a lighter processing load and a lower communication load since data are sent to multiple nodes instead of being sent to the central node. In addition, the user can access the fusion results faster due to less communication delay [8]. Fig. 2, shows the decentralized architecture of WSNs.

Fig. 2. The Decentralized data fusion architecture.

2.3 Hierarchical Architecture

The hierarchical architecture is a combination of the central- ized and the decentralized data fusion architectures. The mo- tivation of using the centralized architecture is to have better accuracy where as using decentralized architecture is useful to decrease computational workload and communication delay [9], [10]. As shown in Fig. 3, all sensor nodes are partitioned
into a hierarchical level. At each level, many sensor nodes send data to the fusion node using suitable routing algorithm to reduce the transmission power. Therefore, the workload is balanced among all nodes in the network [7].

Fig. 3. The Hierarchical data fusion architecture.

3 DATA FUSION TAXONOMY

Data fusion can be categorized into three general taxonomy types, which are: the "relationship among the sources", the "levels of abstraction", and "input and output" [11]. This sec- tion presents all data fusion taxonomies and combines the old and the new taxonomies as shown in Fig. 4.

Fig. 4. All data fusion taxonomies.

3.1 Taxonomy Based on Relationship Among the

Sources

In this section, data fusion is divided into "complementary", "redundant", or "cooperative" [12]. Fig. 5, shows the taxonomy based on the relationship among the sources.
1. Complementary fusion: fuse data from all sensor nodes in order to reach more general information [13], [14].
2. Redundant fusion: data is fused in order to obtain high quality information and thus eliminate transmitting re- dundant data [1].

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1622

ISSN 2229-5518

3. Cooperative fusion: data from independent sources is fused to obtain new data or information such as finding the target location by using angle and distance [1].

Fig. 5. Taxonomy based on the relationship among the sources.

3.2 Taxonomy Based on Levels of Abstraction

The taxonomy based on levels of abstraction is categorized into Low Level fusion, Medium Level fusion, High Level fu- sion, and Multilevel fusion. The details of each level are as follows [15]:
- Low level fusion: it is also called a signal or a measurement
level fusion. Raw data is input which is combined to get more
accurate data as compared to the individual input and thus reduce noise.
- Medium level fusion: also called feature/attribute level fu- sion. The attributes and features of an object are fused in order to provide a feature map that is used for various purposes such as segmentation.
- High level fusion: it is also called "symbol or decision level fusion" [11]. This level of fusion takes symbols as input and further combines them in order to provide a more accurate global decision.
- Multi-level fusion: at this level of fusion, the input and the
output of the data fusion system is one of previous levels. To illustrate this, a decision can be the output of fusing a meas- urement with a feature [15].

3.3 Taxonomy Based on Input and Output

There are five categories of data fusion based on the input and the output of data as Dasarathy stated [16]. These categories are as follows [16]:
1. Data in – data out (DAI-DAO): raw data is an input to
the data fusion system. The output is a raw data as well
but with more reliable data [11] .
2. Data in – feature out (DAI-FEO): raw data is the input
of the data fusion system. The extracted feature or at- tribute of an entity such as object or situation is the out- put.
3. Feature in – feature out (FEI-FEO): the data fusion takes a feature or attribute as an input to get an improved fea-
ture or extracts new features and attributes.
4. Feature in – decision out (FEI-DEO): Data fusion input a
group of features into the system in order to generate
decisions [1].
5. Decision in – decision out (DEI-DEO): data fusion takes decisions as inputs and fuses them to provide new deci- sions as outputs.

3.4 Other Taxonomy of Data Fusion

Zhao and Wang [17] have also introduced a new taxonomy of data fusion in WSNs based on data level, data type, and user’s requirements.

3.4.1 Data Level Fusion

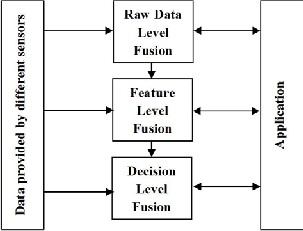
Since data in many applications are fused at various levels, the data fusion is divided into three different levels which are "raw data level, feature level, and decision level" fusion [11]. Examples of applications at raw data level fusion are image enhancement and image compression. At feature level fusion, all characters and attributes of an entity or objects are extract- ed for further processing. At decision level fusion, the result is derived to make decisions [17]. Fig. 6, represents the data level fusion.

Figure 6. The data level fusion.

3.4.2 Data Type Fusion

Based on the data type, there are three types of data fusion. These are as follows: "temporal fusion, spatial fusion and tem- poral–spatial fusion"[11]. The temporal fusion means fusing the data in various time frames but from the same source whereas spatial fusion means fusing the data at the same time but from different sources [17], [11]. Finally, temporal–spatial fusion means fusing data continuously from different nodes over a period of time [17], [11].

3.4.3 Data Fusion based on User’s Requirements

There are three types of data fusion based on user’s require- ment. Sometimes the user needs a single information about a concrete place which can be obtained by a single sensor or the user might need new information regarding a certain area. In addition, the user might need complete information about the overall network [17].

4 DATA FUSION TECHNIQUES AND METHODS

Based on the purpose of the method, data fusion techniques can be implemented for a variety of "objectives such as infer-

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1623

ISSN 2229-5518

ence, estimation, classification, feature maps, abstract sensors, aggregation, and compression" [15]. In this section, many techniques used in data fusion are discussed along with their applications in WSNs. Fig. 7, shows all data fusion techniques used in WSNs.

Fig. 7. Data fusion techniques in W SN.

4.1 Inference Methods

Inference method is mostly used in decision fusion where a decision is generated depending on the perceived situational knowledge. "Classical inference methods are based on Bayesi- an inference and Dempster-Shafer Belief Accumulation theo- ry" [15],[18]. Other inference methods such as fuzzy logic, neural networks, abductive reasoning, and semantic data fu- sion are also highlighted.

4.1.1 Bayesian Inference

Depending on the probability theory, Bayesian Inference merge all evidences where the uncertainty in Bayesian Infer- ence describes the belief. It assumes the value of 0 for absolute disbelief and 1 for absolute belief. Bayesian inference is basi- cally based on the "Bayes’ rule" [19], [15], which is represented in Equation (1):
Pr(B | A ) = (Pr(A | B ) * Pr(B )) / ( Pr(A)) (1) Where, Pr(A | B ) is the belief of hypothesis B given the in-
formation A, Pr(A | B ) is the probability of receiving A, given
that B is true, Pr(B ) is the prior probability, and Pr(A) is the normalizing constant.
The critical issue in Bayesian Inference is that the probabili- ties Pr (A) and Pr (A|B) should be estimated because they are unknown. The neural network approach has been used to guess the conditional probabilities for the decision-making
process in Bayesian inference module [20]. In addition, Cou´E
et al. [21] used Bayesian programming in fusing data from various sensors such as laser and video in order to obtain more reliable and accurate data. In WSNs, Krishnamachari and Iyengar [22] uses Bayesian Inference method for event detection. The inference algorithm in [23] uses Bayesian Infer- ence to detect the missing data from sleep nodes within a sens- ing period.

4.1.2 Dempster-Shafer Inference

This method is based on the "Dempster-Shafer Belief", which generalizes the Bayesian theory. Dempster-Shafer Belief was proposed by both Dempster [24] and Shafer [25]. Dempster- Shafer Inference introduces a formalism that is applied for incomplete knowledge and evidence combination [26]. An important factor in Dempster-Shafer method is the set of all possible states which further demonstrate the system. This set is called the ‘frame of discernment’. The elements of the power set of possible states are called hypotheses. Each hypothesis has its assigned probability. In addition, the belief function which is called ‘bel’ is defined by Dempster-Shafer and also the degree of doubt ‘dou’ that is based on the belief function are [27].
In [28], the authors provided an implementation of both
the "Dempster-Shafer" and the "Bayesian inference" into one
algorithm. The "Dempster-Shafer inference" was used to pro-
vide battlefields' dynamic pictures in a WSN that consists of
"Unmanned Aerial Vehicle (UAV)" as sensor nodes for evalua- tion purposes where in fact the fusion challenges in a mobile network were not evaluated [29]. "Data Service Middleware (DSWare)" in WSNs, by [30], uses this technique where each decision is assigned to a confidence value. This value is calcu- lated by the predetermined confidence function.

4.1.3 Semantic Data Fusion

Semantic data fusion is done as an in-network inference. The semantic data fusion method is composed of two important phases. The first phase is called knowledge base construction, which collects the "knowledge abstractions" into a form of se- mantic data. The second phase is called pattern matching (in- ference), which uses the semantic data provided by the previ- ous phase to fuse relevant attributes for pattern matching [31]. This method was first introduced by Friedlander and Phoha [31] for target classification. Friedlander [32] explains many techniques that extract semantic data from sensors by convert- ing sensor data into formal languages. He applies these tech- niques for the recognition of the robots’ behavior and for sav- ing resources. In [33], users can formulate queries based on semantic values without the knowledge of which data or op- erations are used.

4.1.4 Fuzzy Logic

Fuzzy logic deals with "approximate reasoning" in order to obtain "conclusions from imprecise premises" [34], [1]. Zadeh [35] has introduced the concept of fuzzy sets which later guid- ed him to the fuzzy logic theory. The data fusion algorithm based on fuzzy logic theory has four main phases: "fuzzifica- tion", "rule evaluation", "combination" or "aggregation of

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1624

ISSN 2229-5518

rules", and "deffuzification" [36]. In the second phase which is the rule evaluation, the implications or rules are used to pro- cess the fuzzified inputs. These rules are in the form of “if A then B”, where A is a conditional statement. Sometimes more than two conditional statements are used which is called com- plex implications. When applying complex implications, fuzzy operators are used for computing the final result [37]. The most common fuzzy logic inference operators used are shown in Equations (2), (3), (4), (5), (6), (7), (8), and (9) as follows [37]:
x⟶y = yx (2) x⟶y = min{1,1-x+y} (3) x⟶y = min {x,y} (4)
(5) (6)

(7)

x⟶y = max { 1-x,y} (8)
x⟶y = 1-x+xy (9)
In Equation (4), the Mamdani inference operator is present-
ed. It finds the minimum degree of the membership (x, y).
Both Mamdani and Tsukamoto-Sugeno inference methods are
based on fuzzy logic [38]. However, the Mamdani method is considered a better method since it ensures an efficient data fusion, extends the sensor lifetime, and reduces delay com- pared to Tsukamoto method.
In [39], authors use fuzzy logic control and an intelligent
sensor network for autonomous navigational robotic vehicle which has the ability of avoiding obstacles. Cui et al. [40] use position algorithm based on a fuzzy logic to deal with the un- certain data that the sensors gathered. Moreover, a fuzzy op- timization algorithm is used to update the location of each node. [41], uses fuzzy reasoning to find the best cluster-heads in a WSN. Another implementation of fuzzy logic is for effi- cient routing that minimizes energy usage [42]. Wallace et al. [43] introduced the Medium Access Control (MAC) protocols based on fuzzy logic concept in two stages. The purpose is to extend the network lifetime. The first stage has several inputs such as the current transmit queue size, collision of the previ- ous packages, and remaining battery. The second stage uses the same inputs used in the first stage but with a priority.

4.1.5 Neural Networks

The Neural network is applied in "learning systems" with fuzzy logic to manage its "learning rate" [44], [45], [1]. In the data fusion domain, neural networks have been applied for "Automatic Target Recognition (ATR)" [46]. Neural Networks have been applied in many applications. Lewis and Powers
[47] fused audio-visual information using neural networks for audio-visual speech recognition.

4.1.6 Abductive Reasoning

Abductive Reasoning is the best hypothesis for explaining observed evidence [48]. Fig. 8. shows the deduction and ab- duction example. The abductive inference finds the maximum a posteriori probability [49]. Abduction was used in machine learning problems [50] and diagnosis problems [51].

Fig. 8. The deduction and abduction example

4.2 Estimation Methods

Estimation methods are derived from the control and the probability theories in order to calculate a process vector from a series of measurement vectors [52]. Examples of Estimation methods are Maximum A Posteriori (MAP), Particle filter, Least Squares, Kalman filter, Maximum Likelihood (ML), and Moving Average filter. The details of each method are pre- sented in this section.

4.2.1 Maximum A Posteriori (MAP)

This technique is based on Bayesian theory. Given that ‘a’, is the state to estimate, where ‘b’= {b(1),b(2),..,b(n)} is a set of n observations of ‘a’, the MAP estimator is used to figure out a value of ‘a’ in order to maximize the posterior distribution function [53] as in Equation (10).

(n)=arg⁡maxa pdf(a|b) (10)

where pdf is the probability density function.
MAP estimator was used by Schmitt et al. [54] in a known environment to locate the joint positions of mobile robots. An- other implementation of MAP estimator was by Yuan and Kam [55] in the collision resolution algorithm. The algorithm’s purpose is to control the traffic between the fusion node and the source, where MAP estimator figures out the number of nodes that are being transmitted. Therefore, the retransmis- sion probability of these nodes needs to be updated according- ly.

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1625

ISSN 2229-5518

4.2.2 Particle Filter

These filters are recursive processes of the "sequential Monte Carlo methods (SMC)" [56]. They are suitable for applications that implement a non-Gaussian noise [57]. They use a large number of random measures which are composed of particles (samples) that are driven from distributions and weights of the particles. The random measures are helpful in calculating all kinds of unknown estimates such as minimum mean square error (MMSE) and maximum a posteriori (MAP). The Particle filter technique represents significant densities by par- ticles and weights. It then computes the integrals by Monte Carlo methods. There are three important operations of the Particle filters: sample step which generates particles, im- portance step which computes the particle weights which are later normalized, and the resampling step. The resampling is important as it eliminates the trajectories with small weights and highlights the ones that are dominating [58].
Filters have been used in target tracking problems within
WSNs, such as [59] where Particle filters are used in a tracking
algorithm along with binary detection model. Wong et al. [60]
also used Particle filters in a collaborative data fusion scheme
to fuse information from different sensors for tracking targets. Hu and Evans [61] used this technique in a mobile network to find the nodes’ locations. They argue that mobility enhances accuracy and thus decreases localization costs.

4.2.3 Least Squares

The "Least Squares method is a mathematical optimization technique that searches for a function that best fits a set of in- put measurements. This is accomplished by minimizing the sum of the square error between points generated by the func- tion and the input measurements" [1]. Unlike the "Maximum A Posteriori Probability", this the Least Square does not use any previous probability. Therefore, it works in a determinis- tic manner [15]. The Least Squares method tries to find the value of x [53] as in Equation (11).

(11) Where h is the sensor model for a sequence of 1 ≤ i ≤ n ob-

servations.
The "Huber Loss function" [62], the "ordinary squared er- ror" [53], and the "root mean squared error" [63] are various Square Error metrics. An advantage of using the Least Squares method is reducing the communication between the source node and the sink. This is achieved by sharing the sensor data through the linear regression instead of transmitting the actual data [63]. In addition, these filters were implemented in the sink node as well as in the source node to avoid sending all the data from the source to sink. This is done in a dual predic- tion scheme where the data will be transmitted to the sink node if the predicted and the actual values have a difference more than a given error [64].

4.2.4 Kalman Filter

The Kalman filter is invented by Kalman [65] and it gained popularity as a technique used for data fusion in WSNs. The Kalman filter is shown in Fig. 9. Based on some measurement y(n) which is shown in Equation (12), and the system parame- ters (which are known in advance), the estimate of x(n), and the prediction of x(n + 1) are presented in Equations (13), and (14) respectively.
y(n) = H(n) x(n) + r(n) (12) Where: H(n) is the measurement matrix r is a random variable that follows the zero-mean Gaussian laws.
(n)= (n | n-1)+K(n)[y(n)-H(n) (n | n-1)] (13) Where K is the Kalman filter gain.
(n + 1 | n) = Ts (n) (t | t) + Ti (n)I(n) (14) Where: Ts(n) is the state transition matrix, Ti (n) is the input transition matrix, and I (n) is the input vector.
The Kalman filter technique works well in a linear model where it retrieves optimal estimates recursively [66]. On the other hand, in a nonlinear model, other methods should be used such as "Extended Kalman filter (EKF)" [67], and the "Unscented Kalman Filter (UKF)" [68]. In WSNs, data loss is an issue due to unreliable communication links. [69] evaluated this method's performance based on many observations where they found that at some point the Kalman filter becomes un- steady.
The Kalman filter has also been applied for the purpose of
source localization [53]. It is also used to track different
sources [70]. Others used a "dual Kalman Filter" method in
order to forecast the sensed data. Therefore, when the sink node forecasting is inaccurate, the source node can send data in this situation [71]. In addition, the Kalman filter used in the SCAR routing algorithm to forecast some valuable infor- mation about the nodes’ neighbors. After that, the SCAR rout- ing algorithm would choose the routing path and the best neighbor depending on these predictions [72].

Fig. 9. Kalman filter block diagram

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1626

ISSN 2229-5518

4.2.5 Maximum Likelihood (ML)

To estimate a state ‘a’ as an example, where ‘b’=
{b(1),b(2),..,b(n)} is a set of n observations of ‘a’, the likelihood
function is defined as follows:
λ(a) = p (b |a) (15)
where p is the probability density function.
The Maximum Likelihood estimator (MLE) is used to fig- ure out a value of ‘a’ in order to maximize the likelihood func- tion [53] as in Equation (16).

(16) A new distributed and localized MLE was proposed by

Xiao et al. [73] with more robustness, where each node can
compute a "local unbiased estimate" to eventually reach "the global Maximum Likelihood solution" [15]. This method was further developed by Xiao et al. [74] in order to deliver meas- urements in a timely manner.
Other implementations of MLE that were helpful to reduce
the necessity of sharing all data are the "Decentralized Expec- tation Maximization (EM) algorithm" [75], and the "Local Max- imum Likelihood Estimator" [76]. The MLE is very helpful in location discovery problems such as, to compute distance, direction or angle to know the exact location of nodes or tar- gets. In the case of finding the node location, an example is the "Knowledge-Based Positioning System (KPS)" [77] which has a predefined value of the pdf of the node so that each node es- timates its location using the MLE. Another example is using MLE to find the source location which is provided by Chen et al. [78], where the authors use the bird monitoring application. In the network tomography, MLE was used throughout the aggregation and reporting process for estimating per-node loss rates which has a great impact on routing algorithms es- pecially for robust fault-tolerant protocols [79].

4.2.6 Moving Average Filter

The moving average filter is mainly used in "digital signal processing (DSP) solutions" [15]. It has many advantages such that it is easy to use as it reduces "random white noise" while maintaining a "sharp step response" [15]. For this reasons it is an optimal filter in the time domain for processing encoded signals [80]. The true signal x = ( (1), (2), . .) is estimated by Equation (17).

(17)

Where z=(z(1), z(2), . . .), is the input digital signal, w is the filter’s window that indicates the number of input observa- tions for every n ≥ w.
In addition, w refers to the number of steps needed for the filter to identify the signal level's variance. As the value of w increases, the signal becomes cleaner. In contrast, as the value of w decreases, the step edge becomes sharper. The Moving Average filter is able to decline √w of the white noise variance [80]. Yang et al. [81] have used this technique in target loca-
tions which in turn reduces the chances of inaccuracy of track- ing applications in WSNs. Other types of Moving Average filters in WSNs are "Weighted Moving Average" and "Expo- nentially Weighted Moving Average" (EWMA) filters. The EWMA filter has been used to determine noise in MAC proto- cols [82]. It has other helpful uses in WSNs such as in localiza- tion [83], in detection and classification [84], and local clock synchronization [85].

4.3 Compression

Compression methods are applied in WSN through spatially correlating all sensor nodes with no additional communication cost. This can be obtained by providing two nodes with corre- lated observations [86]. Several compression methods are dis- cussed in this section.

4.3.1 Distributed Source Coding (DSC)

Distributed Source Coding (DSC) [87], is "the compression of multiple correlated sources, physically separated, that do not communicate with each other "[88]. One of the most popular data compression methods in WSNs is the "Distributed Source Coding Using Syndromes" (DISCUS) framework [89]. In DIS- CUS, assuming we have a node X which wants to transmit its observation to node Y. In order to code X’s observation, X can send only an index. There is one requirement which is the Hamming distance between X and Y which is at most one. This means that, the difference of X and Y can be only one bit. Suppose that a sensor observation can be any value of the set S={000, 001, 010, 011, 100, 101, 110, 111}. X and Y have four cosets {000, 111}, {001, 110}, {010, 101}, {100, 011}. As shown in Fig. 10, node X sends the index of 10 which corresponds to the coset of {010, 101}. Y now can decode the index along with its own observation of (100). Since the Hammimg distance should be at most one between the two, Y knows that the value pro- vided by X should be 101 [15].
Critescu et al [90] applied Slepian-Wolf coding which is
based on distributed source coding. It is a kind of distributed
source coding technique that eliminates redundant data due to
the spatially correlated observations in WSNs [91]. Marco and Neuhoff [92] applied Slepian-Wolf coding locally within each cluster. The result was efficient as it mitigates the node’s fail- ure when the data is reconstructed at the sink node.

4.3.2 Coding by Ordering

This technique was first introduced in Petrovic et al. [93]. In this technique, each node sends the data to the border node. The border nodes are responsible for sending what is called a supper-packet, which is a group of all packets, to the sink node. Table 1, gives an example of coding by order. As shown in Table 1, we have four nodes that each of them provides an observation of the value from 0 to 5: X,Y,Z, and W. As shown in Table 1, the border node can suppress all values by W. The ordering is 3! which means that we have 6 possible orderings of the three remaining nodes: X, Y, and Z. For example, if the observation value for node W is 1, the packet order is {X,Z,Y} where it can be {Z,X,Y} if the observation value for node W is 4 and so on [15].
In addition, there are other data compression techniques

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1627

ISSN 2229-5518

that are applied in WSNs. Ju and Cui [94] introduced a com- pression technique called The Easinet Packet Compression (EasiPC) which focuses on the transmitted packet and discov- ers the redundancy within that packet. Recently, researchers have focused on joint data compression. Pattem et al. [95] ar- gue that a static clustering scheme offers near-optimal perfor- mance for spatial correlations.

Fig. 10. An example of DISCUS data compression in W SNs.

TABLE 1

CODE BY ORDERING EXAMPLE.

4.4 Aggregation

According to Kulik et al. [96], data aggregations is defined as a technique that is used for solving two kinds of problems: im- plosion, which occurs when the data sensed is duplicated by the same node because of the strategy used in routing and overlap, which occurs when two different nodes broadcast the same data (redundant sensors) [15]. Redundancy has a nega- tive effect on the network as it wastes the network's energy as well as its bandwidth. Therefore, data aggregation and data fusion are important to reduce energy consumption. For that specific reason, data aggregation is applied for the purpose of reducing redundancy in neighboring nodes [97], [98]. Instead of the classical address-centric approach that was used in data forwarding, a novel data-centric approach is currently used [99]. Each time the sensor node receives information from a neighbor node, it needs to determine whether this information is worth forwarding to other sensor nodes; otherwise it will be a waste of resources. Using data fusion techniques can de- crease the number of packets needed to be transmitted by pro- cessing data locally and then send only a digest to the sink node which in return saves energy and bandwidth. To illus- trate this, the centralized approach takes O (n3/2) bit-hops,
where when applying data fusion techniques it takes only O (n) bit–hops for data transmission [62].
In WSNs, data aggregation proved its benefits to save en- ergy consumption. Krishnamachari et al. [100] have discussed the results of the aggregation tree creation. They analyzed the costs and the delay of data aggregation, and the complexity of optimal data aggregation. In addition, the tradeoff between accuracy and energy consumption have been studied while using aggregation functions in WSNs [101]. Several aggrega- tion functions are used in WSNs such as suppression [97], which discards duplicates and thus eliminates data redundan- cy. Another aggregation function is called packaging [102]. This aggregation function uses a single packet for all observa- tions which reduces the overhead of the MAC protocol every time a packet is sent. Moreover, the greedy aggregation ap- proach outperforms the opportunistic approach in terms of energy savings especially in a network with a high node den- sity [103].
In-network data aggregation algorithms have gained a lot
of attention recently since they require coordination among
nodes when they are distributed in the network to assure high
performance which is basically a complex functionality. In-
network aggregation can be defined as collecting and routing data within a "multi-hop network" where it processes data at intermediate nodes in order to decrease energy consumption and thus increase the network’s lifetime [14]. Regarding in- network aggregation, there are two approaches which are as follows: In-network aggregation with size reduction or with- out size reduction. In the first approach, data from different sources are combined and compressed and further sent over to the network which decreases the information to be sent but reduces the accuracy of the aggregated information at the sink as well. The second approach merges all packets from various sources into one packet with no data processing which keeps the original information and thus ensures high accuracy at the sink node [14].

4.5 An Information Theory Approach

Using multiple sensors instead of a single sensor in any net- work can enhance data and observation reliability. Infor- mation fusion based on multiple sensors are harder to esti- mate in advance. This leads to probabilistic data collection and processing which can be measured and analyzed by applying the information theory principles [104]. In addition, the deci- sion theory is another essential aspect in WSNs [105]. Both the "Information" and "Detection" theories help in solving many problems regarding data fusion. Ahmed and Pottie [106] have used a Bayesian technique for fusion which uses different sen- sor types along with different sensing capabilities. There are interesting tradeoffs between information rate and the distor- tion theory which can be found using entropies [107].

4.6. Reliable Abstract Sensors

This method was first proposed by Marzullo [108] which sug- gests three different types of sensors: "concrete sensor", which senses the environment by collecting samples of a physical variable, "abstract sensor" which represents the observation in a set of values depending on the concrete sensor, and "reliable abstract sensor" which contain the real values of the physical

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1628

ISSN 2229-5518

variable. This type of sensor is computed using a number of abstract sensors. This fusion method has been applied in vari- ous applications in time synchronization [109]. Many algo- rithms and functions that are used with reliable abstract sen- sors for time synchronization such as "Fault-Tolerant Averag- ing" algorithm and "Fault-Tolerant Interval" (FTI) function.

4.6.1 Fault-Tolerant Averaging

This algorithm is used in data fusion methods as it fuses a n number of "abstract sensors" into correct "reliable abstract sen- sors" even if there are incorrect sensors [108]. The algorithm works as follows. Suppose we have L={I1, . . . , In} where Ii = [xi , yi] by n abstract sensors at the same time and we have at most f of n abstract sensors which are incorrect or faulty. The "Fault-Tolerant Averaging" algorithm is shown in Equation (18) which has a complexity of O(nlog n) [108].
Fig. 12 shows the same example as Fig. 11, however the re- sult is not that affected when Sen 2’ is moved (Fig. 12(b)). Therefore, FTI obviously is less vulnerable to small alterations in the input intervals as compared to the Fault-Tolerant Aver- aging algorithm [111].
Where:

(18)
Low refers to the smallest value in at least n − f intervals in L, and High refers to the largest value in at least n − f intervals in L.
Fig. 11, shows two different scenarios of applying the Fault- Tolerant Averaging algorithm where there is one faulty sen- sor. In Fig. 11 (a) Sen 2 and Sen 3 do not have any intersection; therefore, one of them is the faulty sensor. (sen1,sen 2,sen
3 ,sen 4) has {Low,High}, where Low (the left edge of Sen 1)= n
− f = 4 − 1 = 3, and High (the right edge of Sen 4)= n − f = 4 − 1
= 3. However, in Fig.11 (b), the right edge of Sen 2 has moved to the left and becomes Sen 2.
As a result, we have now (sen1,sen 2',sen 3 ,sen 4) which indicates the instability of M. Consequently, the left edge of the result is the left edge of Sen 3 (Low value) and the right edge of the result is the right edge of Sen 4 (High value). This algorithm was further extended by Chew and Marzullo [110] where they fuse data from multidimensional sensors.

4.6.2 The Fault-Tolerant Interval Function

This function was introduced by Schmid and Schossmaier [111]. The Fault-Tolerant Interval (FTI) function is also used in data fusion methods. Again, we have at most f of n abstract sensors considered as incorrect or faulty sensors. FTI function is shown in Equation (19).

(L)={Low,High} (19) Where:

Low refers to the ( f + 1)th largest of the left edges {x1, . . . , xn}
High refers to the ( f + 1)th smallest of the right edges { y1, . . . ,
yn}
FTI function indicates that when there are few alterations
in the input intervals, unlike the Fault-Tolerant Averaging
algorithm, the result will include only few changes as well. As a result, the FTI function is more robust as compared to the Fault-Tolerant Averaging algorithm [111].

Fig. 11. Two different scenarios of applying the "Fault-Tolerant Averag- ing" algorithm where there is a one faulty sensor.

4.7 Feature Maps

Sometimes using raw sensory data is not sufficient especially in guidance and resource management applications. As a re- sult, some features that well describe the environment need to be extracted [18]. Many data fusion methods of inference and estimation produce a feature map. There are two which are occupancy grid and network scans.

4.7.1 Occupancy Grid

Occupancy maps define a 2D/3D representation of the space which is organized in square cells where every cell has an es- timate that indicates its probabilistic occupancy [112]. This probability is calculated by using multiple types of sensors and various data fusion techniques [113]. Occupancy maps are used in many applications such as robot perception [114], the location's estimation [115], and navigation [116].

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1629

ISSN 2229-5518

Fig. 12. Two different scenarios of applying The "Fault-Tolerant Interval" (FTI) function

4.7.2 Network Scans

Network Scans are kinds of activity maps for WSNs. They also give an overview of the resource distribution in the network [117]. One of the most popular network scans is called eScan [117] which provides information about the remaining energy in the network. The algorithm forms an aggregation tree where each node calculates its local eScan and then sends it to the sink. If two or more eScans are received at the same node, an aggregation process is involved to identify the remaining energy of nodes in a specific region. Finally a map is generated [117].

5 EVALUATION AND COMPARISON OF DATA FUSION

TECHNIQUES

This section evaluates all the data fusion techniques presented in this paper and draws a conclusion about which technique is most suitable and reliable to be applied in WSNs.
Both the "Bayesian Inference" and the "Dempster-Shafer" theory are well-known Inference methods. Dempster-Shafer method generalizes Bayesian Inference. However, "Dempster- Shafer theory" is a more flexible method than "Bayesian Infer- ence" due to its capability to fuse data from various types of sensors unlike Bayesian Inference [14]. Another difference between these two techniques is that Dempster-Shafer theory does not require assigning apriori probabilities to unknown propositions [18]. In contrast, Dempster-Shafer involves long- er calculations [118]. In addition, Fuzzy logic method is best
suitable for decision making with uncertain information from multiple sensor nodes. It also improves the quality of infor- mation and thus can be implemented effectively in data fusion in WSN [37]. On the other hand, fuzzy logic cannot solve problems without the knowledge of an expert as it does not have the learning membership function either during solving the problem or after the problem has been solved [119].
Applying neural network in WSNs has many advantages.
In neural network, data fusion is done closely to the source
node which results in enhancing its performance. The algo-
rithm used in neural network draws the important features of
data and can be adjusted to meet the requirement of various applications [120]. It also provides robustness to handle many issues like noise [121]. It identifies various signals and reduces the errors and false alarm rate of the sensors in an efficient manner [122]. However, many issues need to be considered during the implementation of a neural network such as the problem of local extremum, misclassification due to data di- mension increase, and convergence speed of the training [123]. Abductive Reasoning is another technique which works for pattern reasoning more than a data fusion method. It has not been formally used in WSNs but it is used successfully in fault diagnosis and event detection [15].
The semantic data fusion technique has the ability to im-
prove resource utilization especially when collecting and pro-
cessing data in WSNs [15]. This method also reduces transmis-
sion cost because the nodes transmit formal language struc-
ture without the need of transmitting raw data. On the other hand, this technique requires in some scenarios a known set of behaviors in advance, which is a difficult process in specific situations [124].
Moreover, when the state that needs to be estimated is not
based on some random variables, the Maximum Likelihood (ML) technique is suitable to be applied. It also finds the value of this state and assumes it is fixed. In contrast, the "Maximum A Posteriori" (MAP) technique does not consider that the state’s value is fixed. On the other hand, it takes it as the result of some random variables with known prior pdf [53]. In addi- tion, the "Least Squares" technique is more accurate and suita- ble to be applied where the state is fixed. This technique does not use any previous probability as compared to the Maxi- mum A Posteriori (MAP) technique [15]. The Moving Average Filter technique can be used to decrease the random white noise. It has also been used in WSNs to reduce the errors caused by tracking applications [81]. The downside of this technique is that an old value will have the same impact as the most recent measurement which will affect the final result [125].
Kalman filter is an important and powerful technique as it can estimate past, present, and future states [67]. However, when used in WSNs, it needs clock synchronization which can impact its performance [126]. The Kalman filter can be unsta- ble due to the "critical value for the arrival rate of the observa- tions" [69].
Furthermore, Particle filter is an excellent technique used
to overcome some difficult problems such as signal pro-
cessing, navigation, communications, and computer vision.

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1630

ISSN 2229-5518

On the other hand, it has some drawbacks as it is considered a complex technique that has a computational intensity [58].
In addition, even though Occupancy grids show only a re- stricted class of maps which indicate incorrect independence assumptions in prior and posterior distributions, they also have the advantage of being simply applied [127]. The net- work scan technique can be helpful in describing network re- sources and activity. In particular, eScan can guide designers as to where to deploy new sensors since it presents low energy regions [117]. Moreover, the Fault-Tolerant Averaging tech- nique can successfully fuse n number of abstract sensors into correct reliable abstract sensors where in fact there are incor- rect original sensors [108]. However, few alterations in the input intervals can affect the performance of the "Fault- Tolerant Averaging" algorithm [108]. On the other hand, the Fault-Tolerant Interval Function is more robust due to the fact that few alterations in the input intervals will lead to only few alterations in the output [111].
The aggregation technique helps to eliminate redundancy
and traffic load which saves energy in the network. However,
by using this technique, the fusion node can be compromised
by malicious attackers which affect the correctness of the fu-
sion data. Another disadvantage of this technique is that there might be multiple copies of the same fusion results at the sink node which increases the energy consumption at the sink node [7].
Distributed Source Coding (DSC) has the advantage of
making the coding decisions process works efficiently sepa- rated from the routing process. On the other hand, it requires more computational complexity. It also needs to collect some data from joint statistics which is not an easy task [14]. The Code by Ordering technique is simple but does not present all possible correlations between sensor nodes [15]. Finally, the information theory approach is suitable for analyzing many problems regarding data collection and processing by multiple sensors [104].
Table 2, summaries the advantages and the disadvantages
of all data fusion techniques. Based on previous findings, we evaluate the various data fusion techniques discussed in this paper and draw a closure. To conclude, there are various data fusion techniques that have been applied. However, in WSNs, some of these techniques do not concern the specific require- ments of this type of network such as low energy consumption and flexibility. Therefore, for the best applicability of data fu- sion in WSNs, some techniques outweigh others as follows:
1. The Dempster-Shafer is a good technique as it fuses da- ta sensed by different types of sensors which are needed in many applications.
2. The Fuzzy logic technique performs very well in the de-
cision making process and has better data quality.
3. Neural networks enhance the process of data fusion
which is an advantage in WSNs as it saves power con-
sumption.
4. The Semantic data fusion technique saves resources in
WSNs.
5. The Least Squares technique has high accuracy in
WSNs.
6. The Moving Average Filter technique can be used in
WSNs to decrease the chances of errors which also
saves a lot of energy and thus increases the performance
of the network.
7. The Network scan (eScan) can show low power regions
in order to fill in with new full energy sensors.
8. The aggregation technique eliminates redundant data
and thus saves energy.

6 DATA FUSION CHALLENGES IN WIRELESS SENSOR

NETWORKS

There are many challenges that need to be considered while applying data fusion in WSNs. However, it is a challenging task to try to handle all these issues in one data fusion algo- rithm. These issues are as follows:
A. Security:
Although data fusion in WSNs saves power consumption as it
eliminates redundant data and thus enhances the overall per-
formance of the network, it risks the security of the network as
well. It makes the network easily attacked by data intercep-
tion, data falsification, data tampering and data repeated at- tacks. Any attacker can reach security information such as keys by capturing a single node; therefore, all data fusion al- gorithms should guarantee the security of these information even in case of one of the nodes is captured [128].
B. Data Imperfection:
Sometimes the data collected by sensors contain uncertain or
imprecise measurements. Hence, data fusion algorithms
should handle this issue by eliminating data redundancy ef-
fectively [129].
C. Data Correlation:
In WSNs, sensor nodes might be exposed to an external noise
which in turn affect the measurements. The data fusion algo-
rithm should consider data dependencies otherwise it experi-
ence over/under confidence in results [130].
D. Data Dimensionality:
Data collected can be preprocessed at every sensor node (lo-
cally) or at the fusion center (globally) and compressed in or-
der to lower the dimensional data. This is helpful in reducing the power consumption as saving the communication band- width [131].
E. Conflicting Data:
Since in the data fusion system various sources are used,
conflicting data can be occurred due to incomplete data, out- of-date data, or by erroneous data [132].Therefore, a special care is needed when dealing with conflicting data in any data fusion algorithm.

7 CONCLUSION

With the revolution of WSNs and the size, redundancy, inac- curacy of the collected data, researchers have focused on the

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1631

ISSN 2229-5518

data fusion field. Data fusion plays a key role in WSNs as it reduces power consumption and improves the efficiency of the gathered data. Therefore, this paper provides a compre- hensive survey of data fusion in WSNs. Our aim is to focus on the evaluation and the comparison between various data fu- sion techniques. However, some limitations of these tech- niques which have been found need to be considered. Apply- ing data fusion architecture in the WSNs context can face some problems since they are not network-based. However, it can be applied in specific applications in WSNs. There are some challenges need to be handled when developing data fusion algorithms in WSNs.
In future works, we would like to investigate and analyze
further challenges such as the assurance of temporal and spa-
tial correlation while applying data fusion and transmission simultaneously.

TABLE 2

COMPARISON OF DATA FUSION TECHNIQUES.

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1632

ISSN 2229-5518

REFERENCES

[1] A. Abdelgawad and M. Bayoumi, Resource-Aware Data Fusion Algorithms for Wireless Sensor Networks, Boston, MA: Springer US, 2012.

[2] S. V and C. Chandraseka, “Energy Efficient Multipath Data Fu-

sion Technique for Wireless Sensor Networks,” ACEEE Interna- tional Journal on Network Security, vol. 3, no. 8, 2012.

[3] R. Brooks and S. Iyengar, Multi-Sensor Fusion: Fundamentals and Applications with Software, Upper Saddle River, NJ: Prentice- Hall, Inc., 1998.

[4] C. Siaterlis and B. Maglaris, “Towards multisensor data fusion for DoS detection,” In Proceedings of the 2004 ACM Symposium on

IJSER © 2015

Applied Computing. ACM Press, Nicosia, Cyprus, pp. 439–446,

2004.

[5] T. Bass, “Intrusion detection systems and multisensor data fu- sion,” Commun. ACM 2000, vol. 43, no. 2, pp. 99-105, 2000.

[6] A. Savvides, H. Park, and M. Srivastava, “The n-hop multilater- ation primitive for node localization problems,” Mob. Netw, vol.

8, no. 4, pp. 443-451, 2003.

[7] K. Maraiya, K. Kant, and N. Gupta, “Study of Data fusion in Wireless Sensor Network,” In Proceedings of the International Con- ference on Advanced Computing and Communication Technologies (ACCT 2011), Ro'htak, pp. 535-539, 2011.

[8] M. Liggins, C. Chong, I. Kadar, M. Alford, V. Vannicola, and S.

Thomopoulos, “Distributed fusion architectures and algorithms for target tracking,” In Proceedings of the IEEE, vol. 85, no. 1, pp.

http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1633

ISSN 2229-5518

95-107, 1997.

[9] H. Mitchell, Multi-Sensor Data Fusion: An Introduction, NY: Springer, pp. 38–44, 2007.

[10] J. Raol, Multi-Sensor Data Fusion with MATLAB, New York: CRC Press, pp. 21–22, 2010.

[11] P. Neves, J. Rodrigues, and K. Lin, “Data fusion on wireless sen- sor and actuator networks powered by the zensens system,” Communications, IET 2011, vol. 5, no. 12, pp. 1661-1668, 2011.

[12] H. Durrant-Whyte, “Sensor models and multisensor integra- tion,” Int. J. Rob. Res, vol. 7, no. 6, pp. 97-113, 1988.

[13] R. Willett, A. Martin, and R. Nowak, “Backcasting: adaptive sampling for sensor networks,” In Proceedings of the 3rd interna- tional symposium on Information processing in sensor networks, Berkeley, California, USA, 2004.

[14] V. Gupta, and R. Pandey, “Data fusion and topology control in wireless sensor networks,” WSEAS Trans. Sig. Proc, vol. 4, no. 4, pp. 150-172, 2008.

[15] E. Nakamura, A. Loureiro, and A. Frery, “Information fusion for wireless sensor networks: methods, models, and classifications,” ACM Comput. Surv., vol. 39, no. 3, 2007.

[16] B. Dasarathy, “Sensor fusion potential exploitation-innovative architectures and illustrative applications,” Proc. IEEE, vol. 85, no. 1, pp. 24–38, 1997.

[17] C. Zhao, and Y. Wang, “A new classification method on infor- mation fusion of wireless sensor networks,” Int. Conf. on Soft- ware and Systems Symposia (ICESS 1008), Sichuan, China, pp.

231–236, 2008.

[18] V. Borges, and W. Jeberson, “Survey of Context Information Fusion for Sensor Networks based Ubiquitous Systems,” In J. Sens. Actuator Netw, 2013.

[19] T. Bayes, and R. Price, “An essay towards solving a problem in the doctrine of chances,” Philosophical Transactions of the Royal Society, vol. 53 , pp. 370–418, 1763.

[20] H. Pan, Z. Liang, T. Anastasio, and T. Huang, “A hybrid NN- Bayesian architecture for information fusion,” In Proceedings of the 1998 International Conference on Image Processing (ICIP’98), Chicago, IL. 1,pp. 368–371, 1998.

[21] C. Cou´E, T. Fraichard, P. Bessiere, and E. Mazer, “Multi-sensor

data fusion using Bayesian programming: An automotive appli- cation,” In IEEE/RSJ International Conference on Intelligent Robots and System, Lausanne, Switzerland, pp. 141–146, 2002.

[22] B. Krishnamachari, and S. Iyengar, “Distributed Bayesian Algo- rithms for Fault-Tolerant Event Region Detection in Wireless Sensor Networks,” IEEE Transactions on Computers, vol. 53, no. 3, pp. 241-250, 2004.

[23] G. Hartl, and B. Li, “infer: A Bayesian Inference Approach to-

wards Energy Efficient Data Collection in Dense Sensor Net- works,” In Proceedings of the 25th IEEE International Conference on Distributed Computing Systems, pp. 371-380, 2005.

[24] A. Dempster, “A generalization of Bayesian inference,” J. Royal

Stat. Soc., Series B, pp. 205–247, 1968.

[25] G. Shafer, A Mathematical Theory of Evidence, Princeton, NJ: Princeton University Press, 1976.

[26] G. Provan, “A logic-based analysis of Dempster-Shafer theory,”

International Journal of Approximate Reasoning, vol. 4, no. 5, pp.

451–495, 1990.

[27] T. Garvey, J. Lowrance, and M. Fischler, “An inference tech- nique for integrating knowledge from disparate sources,”

In Proceedings of the 7th international joint conference on Artificial intelligence, Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, pp. 319-325, 1981.

[28] A. Pinto, J. Stochero, and J. Rezende, “Aggregation-aware rout- ing on wireless sensor networks,” In Proceedings of the IFIP TC6

9th International Conference on Personal Wireless Communications (PWC’04), Lecture Notes in Computer Science. Delft, The Neth- erlands, pp. 238–247, 2004.

[29] B. Yu, K. Sycara, J. Giampapa, and S. Owens, “Uncertain infor-

mation fusion for force aggregation and classification in air- borne sensor networks,” In AAAI-04 Workshop on Sensor Net- works., AAAI Press, San Jose, CA, 2004.

[30] S. Li, S. Son, and J. Stankovic, “Event detection services using data service middleware in distributed sensor networks,” In Proceedings of the 2nd international conference on Information pro- cessing in sensor networks (IPSN'03); Zhao, F.; Guibas, L., Eds.;

.Springer-Verlag: Berlin, Heidelberg, pp. 502-517, 2003.

[31] D. Friedlander and S. Phoha, “Semantic information fusion for coordinated signal processing in mobile sensor networks,” Int. J. High Perf. Comput. 16, pp. 235–241, 2002.

[32] D. Friedlander, “Semantic information extraction,” In Distributed Sensor Networks;S. S. Iyengar, S.S.; Brooks, R.R., Eds., CRC Press, Boca Raton, pp. 409–417, 2005.

[33] K. Whitehouse, F. Zhao, and J. Liu, “Semantic streams: a framework for composable semantic interpretation of sensor da- ta,” In Proceedings of the Third European conference on Wire- less Sensor Networks, Zurich, Switzerland, 2006.

[34] V. Novák, I. Perfilieva, and J. Močkoř, Mathematical Principles of Fuzzy Logic, The International Series in Engineering and Com- puter Science, , Norwell, MA: Kluwer Academic Publishers,

1999.

[35] L Zadeh, Fuzzy sets, fuzzy logic, and fuzzy systems, selected pa- pers by Lotfi A. Zadeh. NJ: World Scientific Publishing Co., Inc, pp. 94–102, 1996.

[36] J. Jang, C. Sun, and E. Mizutani, A Computational Approach to

Learning and Machine Intelligence, New Jersey: Prentice Hall,

1997.

[37] W. Su and T. Bougiouklis, “Modeling of data fusion algorithms in cluster-based Wireless Sensor Networks,” Signals, Systems and Computers, 42nd Asilomar Conference on, Pacific Grove, CA, pp.

868-872, 2008.

[38] W. Su, and T. Bougiouklis, “Data fusion algorithms in cluster- based wireless sensor networks using fuzzy logic theory,” In Proceedings of the 11th Conference on 11th WSEAS International Conference on Communications (ICCOM'07), World Scientific and Engineering Academy and Society (WSEAS), Stevens Point, Wis- consin, USA, 2007; Mastorakis, N.E.; Kartalopoulos, S.; Simian, D.; Varonides, A.; Mladenov, V.; Bojkovic, Z.; Antonidakis, E., Eds., pp. 291-299, 2007.

[39] W. Chan Yet and U. Qidwai, “Intelligent sensor network for

obstacle avoidance strategy,” In Proceedings of IEEE Conference on

Sensors, pp. 405–408, 2005.

[40] X. Cui, T. Hardin, R. Ragade, and A. Elmaghraby, “A swarm- based fuzzy logic control mobile sensor network for hazardous contaminants localization,” In Proceedings of the 1st IEEE Interna- tional Conference on Mobile Ad-hoc and Sensor Systems (MASS’04). IEEE, Fort Lauderdale, pp. 194–203, 2004.

[41] I. Gupta, D. Riordan, and S. Sampalli, “ Cluster-head election

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1634

ISSN 2229-5518

using fuzzy logic for wireless sensor networks,” In Proceedings of the 3rd Annual Communication Networks and Services Research Conference (CNSR’05). IEEE, Halifax, Canada, pp. 255–260, 2005.

[42] M. Yusuf and T. Haider, “Energy-aware fuzzy routing for wire-

less sensor networks,” In IEEE International Conference on Emerg- ing Technologies (ICET’05). IEEE, Islamiabad, Pakistan, pp. 63–69,

2005.

[43] J. Wallace, D. Pesch, S. Rea, and J. Irvine, “Fuzzy logic optimisa- tion of MAC parameters and sleeping duty-cycles in wireless sensor networks,” In 62nd Vehicular Technology Conference, VTC-

2005-Fall.. IEEE, Dallas, TX, pp. 1824–1828, 2005.

[44] L. Zadeh, “ Fuzzy logic: computing with words,” Fuzzy Systems, IEEE Transactions., vol. 4, no. 2, pp. 103–111, 1996.

[45] P. Bonissone, “Soft computing: The convergence of emerging

reasoning technologies,” Soft Comput, vol. 1, no. 1, pp. 6-18,

1997.

[46] M. Roth, “Survey of neural network technology for automatic target recognition,” Trans. Neur. Netw, vol. 1, no. 1, pp. 28-43,

1990.

[47] T. Lewis and D. Powers, “Audio-visual speech recognition us- ing red exclusion and neural networks,” In Proceedings of the twenty-fifth Australasian conference on Computer science, Mel- bourne, Victoria, Australia, pp. 149-156, 2002.

[48] C. Peirce, “Abduction and induction,” In Philosophical Writings of

Peirce, Peirce, C. S.; Buchler, J., Eds.; Dover, New York, pp. 150–

156, 1955.

[49] L. de Campos, J. Gamez, and S. Moral, “Partial abductive infer- ence in Bayesian belief networks – an evolutionary computation approach by using problem-specific genetic operators,” IEEE Transactions on Evolutionary Computation 2002, vol. 6, no. 2, pp.

105-131, 2002.

[50] R. Mooney, “Integrating abduction and induction in machine learning,” In Abduction and Induction, Essays on their Relation and Integration,; Flach, P.A.; Kakas, A.C., Eds.; Applied Logic Series. Kluwer: New York, 336p, 2000.

[51] J. Aguero and A. Vargas, “Inference of operative configuration of distribution networks using fuzzy logic techniques—part II: Extended real-time model,” IEEE Trans. Power Syst, vol. 20, no.

3, pp. 1562–1569, 2005.

[52] B. Bracio, W. Hom, and D. Moller, “Sensor fusion in biomedical systems,” In Proceedings of the 19th Annual International Confer- ence of the IEEE Engineering in Medicine and Biology Society. IEEE, Chicago, IL, vol. 3, pp. 1387–1390, 1997.

[53] C. Brown, H. Durrant-Whyte, J. Leonard, B. Rao, and B. Steer,

Distributed data fusion using Kalman filtering: A robotics application, In Data Fusion in Robotics and Machine Intelligence, San Diego, CA, Abidi, M.A.; Gonzalez, R.C. Eds, pp. 267–309, 1992.

[54] T. Schmitt, R. Hanek, M. Beetz, S. Buck, and B. Radig, “Cooper- ative probabilistic state estimation for vision-based autonomous mobile robots,” IEEE Trans. Robotics Autom., vol. 18, no. 5, pp.

670–684, 2002.

[55] Y. Yuan and M. Kam, “Distributed decision fusion with a ran- dom-access channel for sensor network applications,” IEEE Trans. Instr. Meas., vol. 53, no. 4, pp. 1339-1344, 2004.

[56] D. Crisan and A. Doucet, “A survey of convergence results on particle filtering methods for practitioners,” IEEE Transactions on Signal Processing, vol. 50, no. 3, pp. 736-746, 2002.

[57] P. Nordlund, F. Gunnarsson, and F. Gustafsson, “Particle filters

for positioning in wireless networks,” In Proceedings of the XI Eu- ropean Signal Processing Conference (EURSIPCO'02). TeSA, Tou- louse, France, pp. 311-314, 2002.

[58] M. Bolic, “Architectures for Efficient Implementation of Particle

Filters,” Ph.D. Dissertation, State University of New York at Stony Brook, Stony Brook, NY, USA, Advisor(s) Petar M. Djuric. AAI3149104, 2004.

[59] J. Aslam, Z. Butler, F. Constantin, V. Crespi, G. Cybenko, and D.

Rus, “Tracking a moving object with a binary sensor network,” In Proceedings of the 1st international conference on Embedded net- worked sensor systems, Los Angeles, California, USA, 2003.

[60] Y. Wong, J. Wu, L. Ngoh, and W. Wong, “Collaborative Data

Fusion Tracking in Sensor Networks using Monte Carlo Meth- ods,” In Proceedings of the 29th Annual IEEE International Confer- ence on Local Computer Networks, pp. 563-564, 2004.

[61] L. Hu and D. Evans, “Localization for mobile sensor networks,” In Proceedings of the 10th annual international conference on Mobile computing and networking, Philadelphia, PA, USA, 2004.

[62] M. Rabbat and R. Nowak, “Distributed optimization in sensor

networks,” In Proceedings of the 3rd international symposium on In- formation processing in sensor networks, Berkeley, California, USA,

2004.

[63] C. Guestrin, P. Bodik, R. Thibaux, M. Paskin, and S. Madden, “Distributed regression: an efficient framework for modeling sensor network data,” In Proceedings of the 3rd international sym- posium on Information processing in sensor networks. Berkeley, Cali- fornia, USA, 2004.

[64] S. Santini and K. R¨omer, “An adaptive strategy for quality-

based data reduction in wireless sensor networks,” In Proceed- ings of the 3rd International Conference on Networked Sensing Sys- tems (INSS). TRF, Chicago, IL, pp. 29-36, 2006.

[65] R. Kalman, “A new approach to linear filtering and prediction

problems,” Trans. ASME J. Basic Engin, vol. 82, no. 1, pp. 35-45,

1960.

[66] R. Luo and M. Kay, “Data fusion and sensor integration: State- of-the-art 1990s,” In Data Fusion in Robotics and Machine Intelli- gence, Abidi, M.A.; Gonzalez, R.C., Eds., Academic Press, Inc., San Diego, CA, pp. 7-135, 1992.

[67] G. Welch and G Bishop, “An Introduction to the Kalman Fil- ter,” University of North Carolina at Chapel Hill, Chapel Hill, NC, 1995.

[68] S. Julier and J. Uhlmann, “A new extension of the Kalman filter to nonlinear systems,” In Signal Processing, Sensor Fusion, and Target Recognition VI. SPIE, San Diego, pp. 182—193, 1997.

[69] B. Sinopoli, L. Schenato, M. Franceschetti, K. Poolla, M. Jordan,

and S. Sastry, “Kalman filtering with intermittent observations,”

IEEE Trans. Autom. Cont., vol. 49, no. 9, pp. 1453-1464, 2004.

[70] T. Li, A. Ekpenyong, and Y. Huang, “Source Localization and Tracking Using Distributed Asynchronous Sensors,” IEEE Transactions on Signal Processing, vol. 54, no. 10, pp. 3991-4003,

2006.

[71] A. Jain, E. Chang, and Y. Wang, “Adaptive stream resource management using Kalman Filters,” In Proceedings of the 2004

ACM SIGMOD international conference on Management of data. Paris, France, 2004.

[72] C. Mascolo and M. Musolesi, “SCAR: context-aware adaptive

routing in delay tolerant mobile sensor networks.” In Proceed- ings of the 2006 international conference on Wireless communications

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1635

ISSN 2229-5518

and mobile computing. Vancouver, British Columbia, Canada, 2006. [73] L. Xiao, S. Boyd, and S. Lall, “A scheme for robust distributed

sensor fusion based on average consensus,” In Proceedings of the

4th international symposium on Information processing in sensor networks, Los Angeles, California, 2005.

[74] L. Xiao, S. Boyd, and S. Lall, “A space-time diffusion scheme for

peer-to-peer least-squares estimation,” In Proceedings of the 5th international conference on Information processing in sensor net- works, Nashville, Tennessee, USA, 2006.

[75] R. Nowak, “Distributed em algorithms for density estimation

and clustering in sensor networks,” IEEE Trans. Sig. Proc., vol.

51, no. 8, pp. 2245-2253, 2003.

[76] D. Blatt and A. Hero, “Distributed maximum likelihood estima- tion for sensor networks,” In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’04). IEEE, Montreal, Canada, pp. 929–932, 2004.

[77] L. Fang, W. Du, and P. Ning, “A beacon-less location discovery

scheme for wireless sensor networks,” In Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM), pp. 161–171, 2005.

[78] C. Chen, A. Ali, and H. Wang, “Design and testing of robust

acoustic arrays for localization and enhancement of several bird sources,” In Proceedings of the 5th international conference on In- formation processing in sensor networks, Nashville, Tennessee, USA,

2006.

[79] G. Hartl and B. Li, “Loss inference in wireless sensor networks based on data aggregation,” In Proceedings of the 3rd international symposium on Information processing in sensor networks, Berkeley, California, USA, 2004.

[80] S. Smith, The scientist and engineer's guide to digital signal pro-

cessing, San Diego, CA: California Technical Publishing, 1997. [81] C. Yang, S. Bagchi, and W. Chappell, “Location tracking with

directional antennas in wireless sensor networks,” In 2005 IEEE MTT-S International Microwave Symposium Digest. IEEE, Long Beach, CA, 2005.

[82] J. Polastre, J. Hill, and D. Culler, “Versatile low power media

access for wireless sensor networks,” In Proceedings of the 2nd in- ternational conference on Embedded networked sensor systems. Balti- more, MD, USA, 2004.

[83] J. Blumenthal, D. Timmermann, C. Buschmann, S. Fischer, J.

Koberstein, and N. Luttenberger, “Minimal transmission power as distance estimation for precise localization in sensor net- works,” In Proceedings of the 2006 international conference on Wire- less communications and mobile computing, Vancouver, British Co- lumbia, Canada, 2006.

[84] L. Gu, D. Jia, P. Vicaire, T. Yan, L. Luo, A. Tirumala, Q. Cao, T.

He, J. Stankovic, T. Abdelzaher, and B. Krogh, “Lightweight de- tection and classification for wireless sensor networks in realis- tic environments,” In Proceedings of the 3rd international confer- ence on Embedded networked sensor systems, San Diego, California, USA, 2005.

[85] I. Rhee, A. Warrier, M. Aia, and J. Min, “ Z-MAC: a hybrid MAC

for wireless sensor networks,” In Proceedings of the 3rd interna- tional conference on Embedded networked sensor systems. San Diego, California, USA, 2005.

[86] A. Hoang and M. Motani, “Collaborative Broadcasting And

Compression In Cluster-Based Wireless Sensor networks,” In

Proceedings of the Second European Workshop on Wireless Sensor

Networks (EWSN'05). IEEE. Istanbul, Turkey, pp. 197-206, 2005. [87] Z. Xiong, A. Liveris, and S. Cheng,” Distributed source coding

for sensor networks,” IEEE Sig. Proc. Mag, vol. 21, no. 5, pp. 80-

94, 2004.

[88] E. Nakamura and A. Loureiro, “Information fusion in wireless sensor networks,” In Proceedings of the 2008 ACM SIGMOD in- ternational conference on Management of data (SIGMOD '08). ACM, New York, NY, USA, pp. 1365-1372, 2008.

[89] S. Pradhan and K. Ramchandran, “Distributed source coding

using syndromes (DISCUS): design and construction,” IEEE Transactions on Information Theory, vol. 49, no. 3, pp. 626-643,

2003.

[90] R. Critescu et al., “Networked slepian-wolf: theory, algorithms, and scaling laws,” IEEE Trans. on Inform. Theory, vol. 51, no. 12, pp. 4057-4073, 2005.

[91] D. Slepian and J. Wolf, “Noiseless encoding of correlated infor- mation sources,” IEEE Trans. Information Theory IT-19, vol. 19, no. 4, pp. 471-480, 1973.

[92] D. Marco and D. Neuhoff, “Reliability vs. efficiency in distribut- ed source coding for field-gathering sensor networks,” In Pro- ceedings of the 3rd international symposium on Information pro- cessing in sensor networks, Berkeley, California, USA, 2004.

[93] D. Petrovic, R. Shah, K. Ramchandran, and J. Rabaey, “Data

funneling: routing with aggregation and compression for wire- less sensor networks,” In Sensor Network Protocols and Applica- tions, 2003. Proceedings of the First IEEE 2003 IEEE International Workshop on, pp. 156–162, 2003.

[94] H. Ju and L. Cui, “EasiPC: A Packet Compression Mechanism

for Embedded WSN,” In Proceedings of the 11th IEEE International Conference on Embedded and Real-Time Computing Systems and Ap- plications, Hong Kong, China, pp. 394-399, 2005.

[95] S. Pattem, B. Krishnamachari, and R. Govindan, “The impact of

spatial correlation on routing with compression in wireless sen- sor networks,” In Proceedings of the 3rd international symposium on Information processing in sensor networks, Berkeley, California, USA,

2004.

[96] J. Kulik, W. Heinzelman, and H. Balakrishnan, “Negotiation- based protocols for disseminating information in wireless sen- sor networks,” Wireless Networks, vol. 8, no. 2-3, pp. 169-185,

2002.

[97] C. Intanagonwiwat, R. Govindan, and D. Estrin, “Directed dif- fusion: a scalable and robust communication paradigm for sen- sor networks,” In Proceedings of the 6th annual international confer- ence on Mobile computing and networking. Boston, Massachusetts, USA, pp. 56-67, 2000.

[98] C. Intanagonwiwat, R. Govindan, D. Estrin, J. Heidemann, and

F. Silva, “Directed diffusion for wireless sensor networking,”

IEEE/ACM Transactions on Networking (TON), vol. 11, no. 1, pp.

2-16, 2003.

[99] A. Woo, T. Tong, and D. Culler, “Taming the underlying chal- lenges of reliable multihop routing in sensor networks,” In Pro- ceedings of the 1st international conference on Embedded networked sensor systems. Los Angeles, California, USA, 2003.

[100]B. Krishnamachari, D. Estrin, and S. Wicker, “The Impact of Da-

ta Aggregation in Wireless Sensor Networks,” In Proceedings of the 22nd International Conference on Distributed Computing Sys- tems, pp. 575-578, 2002.

[101]A. Boulis, S. Ganeriwal, and M. Srivastava, “Aggregation in

IJSER © 2015 http://www.ijser.org

The research paper published by IJSER journal is about Data Fusion in WSNs: Architecture, Taxonomy, Evaluation of Techniques, and Challenges, published in IJSER Volume 6, Issue 4, April 2015 Edition. 1636

ISSN 2229-5518

sensor networks: An energy-accuracy trade-off,” Ad Hoc Net- works, pp. 317-331, 2003.

[102]T. He, B. Blum, J. Stankovic, and T. Abdelzaher, “AIDA: Adap- tive application independent data aggregation in wireless sen- sor network,” ACM Trans. Embed. Comput. Syst., vol. 3, no. 2, pp.

426–457, 2004.

[103]C. Intanagonwiwat, D. Estrin, R. Govindan, and J. Heidemann, “Impact of Network Density on Data Aggregation in Wireless Sensor Networks,” In Proceedings of the 22 nd International Con- ference on Distributed Computing Systems (ICDCS'02), pp. 457-458,

2002.

[104]P. Varshney, Distributed Detection and Data Fusion, Secaucus, NJ: Springer-Verlag New York, Inc., 1996.

[105]H. Poor, An introduction to signal detection and estimation , 2nd

ed.., New York, NY: Springer-Verlag New York, Inc, 1994. [106]M. Ahmed and G. Pottie, Fusion in the context of information theo-

ry, In Distributed Sensor Networks, ; Iyengar, S.S.; Brooks, R.R., Eds.; CRC Press: Boca Raton, pp. 419-436, 2005.

[107]R. Gallager, Information Theory and Reliable Communication, New

York, NY: John Wiley & Sons, Inc., 1968.

[108]K. Marzullo, “Tolerating failures of continuous-valued sensors,”

ACM Transactions on Computer Systems (TOCS), vol. 8, no. 4, pp.

284-304, 1990.

[109]K. R¨Omer, P. Blum, and L. Meier, “Time synchronization and calibration in wireless sensor networks,” In Handbook of Sensor Networks: Algorithms and Architectures, I. Stojmenovic, Ed., Hoboken, NJ: John Wiley & Sons, pp. 199—237, 2005.

[110]P. Chew and K. Marzullo, “Masking failures of multidimention- al sensors,” In Proceedings of the 10th Symposium on Reliable Dis- tributed Systems. IEEE, Pisa, Italy, pp. 32-41, 1991.

[111]U. Schmid and K. Schossmaier, “How to reconcile fault-tolerant interval intersection with the Lipschitz condition,” Distributed Computing, vol. 14, no. 2, pp. 101-111, 2001.

[112]A. Elfes, “Using Occupancy Grids for Mobile Robot Perception and Navigation,” Computer, vol. 22, no. 6, pp. 46-57, 1989.

[113]M. Ribo and A. Pinz, “A comparison of three uncertainty calculi for building sonar-based occupancy grids,” Robotics and Auton- omous Systems, vol. 35, no. 3-4, pp. 201—209, 2001.

[114]A. Hoover and B. Oslen, “Sensor network perception for mobile robotics,” In Proceedings of the IEEE International Conference on Robotics and Automation, pp. 342-347, 2000.

[115]C. Wongngamnit and D. Angluin, “Robot localization in a grid,”

Information Processing Letters, vol. 77, no. 5-6, pp. 5-6, 2001. [116]D. Pagac, E. Nebot, and H. Durrant-Whyte, “An evidential ap-

proach to map-building for autonomous vehicles,” IEEE Trans. Robotics Autom, vol. 14, no. 4, pp. 623—629, 1998.

[117]Y. Zhao, R. Govindan, and D. Estrin, “Residual energy scans for

monitoring wireless sensor networks,” In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC'02),

IEEE, Orlando, FL, pp. 356—362, 2002.

[118]D. Koks and S. Challa, “An introduction to bayesian and demp- ster-shafer data fusion,” Defence Science and Tech Org, 2003.

[119]A. Ibrahim, Fuzzy Logic for Embedded Systems Applications, New- ton, MA: Butterworth-Heinemann, 2003.

[120]W. Sung, and C. Hsiao, “IHPG algorithm for efficient infor- mation fusion in multi-sensor network via smoothing parameter optimization,” Informatica, vol. 24, no. 2, pp. 219-230, 2013.

[121]P. Castelaz, “Neural networks in defense applications,” In Pro- ceedings of the IEEE International Conference on Neural Networks, IEEE, San Diego, CA, pp. 473-480, 1988.

[122]W. Sung, and M. Tsai, “ Multi-sensor wireless signal aggrega-

tion for environmental monitoring system via multi-bit data fu- sion,” Applied Mathematics&Information Sciences, vol. 5, no. 3, pp.

589-603, 2011.

[123]Y. Zeng, J. Zhang, and J. Genderen, “Comparison and analysis of remote sensing data fusion techniques at feature and decision levels,” In ISPRS 2006 : ISPRS mid-term symposium 2006 remote sensing : from pixels to processes, 2006.

[124]F. Castanedo, “A Review of Data Fusion Techniques,” The Scien- tific World Journal. Article ID 704504. 19 pages, 2013.

[125]M. Ghahroudi and R. Sabzevari, “Multisensor Data Fusion Strategies for Advanced Driver Assistance Systems,” In Sensor Data Fusion; I-Tech Education and Publishing KG, pp. 141-166,

2009.

[126]S. Ganeriwal, R. Kumar, and M. Srivastava, “Timing-sync pro- tocol for sensor networks,” In Proceedings of the 1st international conference on Embedded networked sensor systems, 2003.

[127]M. Paskin and S. Thrun, “Robotic mapping with polygonal ran- dom fields,” In Proceedings of the Conference on Uncertainty in Ar- tificial Intelligence, pp. 450–458, 2005.

[128]L. Li and F. Bai, “Analysis of Data Fusion in Wireless Sensor Networks,” In Proceedings of the 2011 international conference on Electronics, Communications and Control (ICECC), pp. 2547-2549,

2011.

[129]B. Khaleghi, A. Khamis, F. Karray, and S. Razavi, “Multisensor data fusion: A review of the state-of-the-art,” Inf. Fusion, vol. 14, no. 1, pp. 28-44, 2013.

[130]B. Khaleghi, S. Razavi, A. Khamis, F. Karray, and M. Kamel, “Multisensor data fusion: Antecedents and directions,” Signals, Circuits and Systems (SCS), 2009 3rd International Conference on, Medenine, pp. 6-8, 2009.

[131]Y. Zhu, E. Song, J. Zhou, and Z. You, “Optimal dimensionality

reduction of sensor data in multisensor estimation fusion,” IEEE Transactions on Signal Processing, vol. 53, no. 5, pp. 1631-1639,

2005.

[132]L. Dong and F. Naumann, “Data fusion: resolving data conflicts for integration,” Proc. VLDB Endow, vol. 2, no. 2, pp. 1654-1655.

2009.

IJSER © 2015 http://www.ijser.org