International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 1
ISSN 2229-5518
Mrs.Yogita Savant 1 Mrs.L.S Admuthe2
Abstract
Computer technology to human needs that touch every aspect of life, ranging from household appliances to robots
for the expedition in space. The development of Internet and multimedia technologies that grow exponentially, resulting in the amount of information managed by computer is necessary. This causes serious problems in storage and transmission image data. Therefore, should be considered a way to compress data so that the storage capacity required will be smaller. The emergence of artificial neural networks in image processing has led to improvements in image compression. In this paper we have discussed method for image compression based on well known KSOFM (Kohonen’s self organizing feature map) neural network.
Index items: Neural Networks, Image compression, self organizing feature map (SOFM), PSNR, IF.
mage compression is a key technology in the field of communications and multimedia applications. Apart from
the existing technology on image compression represented by
series of JPEG, MPEG and H.26x standards, new technology
such as neural networks and genetic algorithms are being developed to explore the future of image coding. Successful applications of neural networks to back propagation algorithm have now become well established and other aspects of neural network involvement in this technology.
The main objective of image compression is to decrease the redundancy of the image data which helps in increasing the capacity of storage and efficient transmission. Image compression aids in decreasing the size in bytes of a digital image without degrading the quality of the image to an undesirable level. There are two classifications in image compression: lossless and lossy compression. The reduction in file size allows more images to be stored in a given amount of disk or memory space. This supports in decreasing the time required for the image to send or download from internet. Research activities on neural networks for image compression do exist in many types of networks such as –Multi Layer perceptron (MLP) [2-3], Hopfield [14], Self-Organizing Map (SOM), Learning Vector Quantization (LVQ)[5], and Principal Component Analysis (PCA) [1].
Artificial neural network models are specified by network topology and learning algorithms [1],[2]. Network topology describes the way in which the neurons (basic processing unit) are interconnected and the way in which they receive input and output. Learning algorithms specify an initial set of weights and indicate how to adapt them
during learning in order to improve network performance.
A neural network can be defined as a “massively parallel distributed processor that has a natural propensity for storing experiential knowledge and making it available for
use”. A number of simple computational units, called
neurons are interconnected to form a network, which perform complex computational tasks. Because of its parallel architecture, Artificial Neural Networks have been applied to image compression problems, due to their superiority over traditional methods when dealing with noisy or incomplete data. Artificial Neural networks seem to be well suited to image compression, as they have the ability to preprocess input patterns to produce simpler patterns with fewer components. This compressed information preserves the full information obtained from the external environment. Neural Networks based techniques provide sufficient compression rates of the data fed to them, also security is easily maintained. Many different training algorithms and architectures have been used. Different types of Artificial Neural Networks have been trained to perform Image Compression. In image compression technique, the compression is achieved by training a neural network with the image and then using the weights and the coefficients from the hidden layer as the data to recreate the image.
Since neural networks are capable of learning from input information and optimizing itself to obtain the appropriate environment for a wide range of tasks, a family of learning algorithms have been developed for vector quantization. In vector quantization (VQ), the input vector is constructed from a K-dimensional space [13].
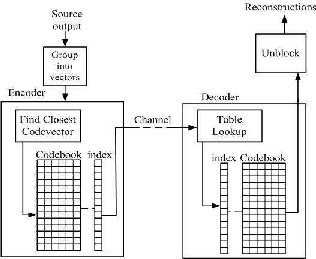
VQ is a lossy compression technique. First, the image is split into square blocks of size p x p (4x4 or 8x8) pixels; each block is considered as a vector in a 16 or 64 dimensional spaces. Second, a limited number of vectors (code words) in this space are selected in order to approximate as much as possible, the distribution of initial vectors extracted from the image. Third, each vector from the original image is replaced by its nearest codeword. Finally, during transmission, the index of the codeword is transmitted. Compression is achieved if the number of bits used to transmit the index is less than the number of initial bits of the block (p x p x m); where m is the number of bits per pixel.
IJSER @ 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 2


ISSN 2229-5518
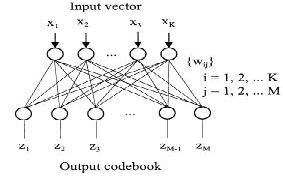
Fig. 2. SOFM neural network
Fig. 1 Compression by Vector quantization
A number of researchers have successfully used the KSOFM (Kohonen self organizing feature map) algorithm to generate VQ codebooks and have demonstrated a number of advantages [13]. KSOFM’s have two properties. First, it quantizes the space like any other vector quantization method, what constitutes a first (lossy) compression of the image. Then, the topology preserving property of KSOFM, coupled with the hypothesis that consecutive blocks in the image will often be similar, and to a differential entropic coder, constitutes a second (non-lossy) compression of the information. This means Vector quantization neural nets can give better compression ratios than other networks.
SOFM is realized by a two-layer network, as shown in Fig. 2. The first layer is the input layer or fan-out layer with neurons and the second layer is the output or competitive layer. The two layers are completely connected. An input vector x € Rk , (Rk is input space) when applied to the input layer, is distributed to one of the (m× n) output nodes (z1-zM) in the competitive layer. Each node in this layer is connected to all nodes in the input layer; hence, it has a weight vector prototype wi, j attached to it.
In SOFM, each data from data set recognizes them by
weight can learn decreases over time. This whole process is repeated a large number of times, usually more than 1000 times. [4]
In sum, learning occurs in several steps and over much iteration:
1. Each node's weights are initialized.
2. A vector is chosen at random from the set of training data.
3. Every node is examined to calculate which one's weights
are most like the input vector. The winning node is commonly known as the Best Matching Unit (BMU).
4. Then the neighborhood of the BMU is calculated. The amount of neighbors decreases over time.
5. The winning weight is rewarded with becoming more like the sample vector. The neighbors also become more like the
sample vector. The closer a node is to the BMU, the more its weights get altered and the farther away the neighbor is from the BMU, the less it learns.
6. Repeat step 2 for N iterations.
Image quality describes the fidelity with which an image compression scheme recreates the source image data. The parameters to judge image compression algorithms are:
competing for representation. The weight vectors initialization is the starting process of SOFM mapping [4].
CR (1 ( No / Ni )) x100 %.........
..........
....( 1)
Then the sample vector is randomly selected and the map of
weight vectors is searched to find which weight best
represents that sample. Each weight vector has neighboring
weights that are close to it. The weight that is chosen is
rewarded by being able to become more like that randomly selected sample vector.
For better compression performance CR must be high.
The neighbors of those weights are also rewarded by 2
being able to become more like the chosen sample vector.
MSE
1
M 1N 1
Xˆ i, j X i, j)
.....( 2 )
From this step the number of neighbors and how much each
i 0 j 0
IJSER @ 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 3
ISSN 2229-5518

Where M*N is the size of the image, X (i, j) and X (i, j) are the
matrix element of the decompressed and the original image at
(i, j)th pixel.
3.3 Peak Signal-to-Noise Ratio: - Peak signal to reconstructed image measure is known as PSNR.
PSNR
10 log
![]()
M * N ............(3)
10 MSE
Fig. 3. Standard Image -Lena_gray.tif compressed by KSOFM neural network. (left) -Original image, (right) - decompressed image
Table.1
AD (average difference), SC(structural content) & IF (image fidelity)[18] are the co relational based quality measures which normally look at correlation features between the pixels of original and reconstructed image, they are given as,
RESULTS FOR IMAGE LENA GRAY
M N ^
X(i, j) X(i, j)
![]()
AD i 0 j0
MN
......... ......... .........(4)

![]()
M N M N ^
SC X (i, j) 2 X (i, j) 2 .......... .......... .(5)
i 1 j1
i1 j1
![]()
M N ^
X(i, j) X(i, j) 2
IF 1 i 1 j1
.......... .........( 6)
Fig.4. Standard Image cameraman.tif compressed by KSOFM neural
X(i, j) 2
i 1 j1
network. (Left)- Original image, (right) - Decompressed image.
Table.2
RESULTS FOR IMAGE CAMERAMAN
These characteristics are used to determine the suitability of a
given compression algorithm for any application.
In order to evaluate the performance of the proposed approach of image compression using SOFM algorithm based vector quantization, standard images are considered. The work is implemented using MATLAB. Lena and Cameraman are the two images used to explore the performance of the proposed approach. The experiments are carried out with the number of clusters of 64, 128 and 256. The evaluation of the proposed approach of image compression is formulated using the performance parameters. The experimentation with codebook trained using Lena image was carried out and it has been observed that this codebook perform well for most of the facial images. Following tables shows the results obtained using the software, MAT LAB 7.0.
In this paper we have discussed the VQ-KSOFM neural network for the image compression. KSOFM based neural networks can give better compression ratios along with good PSNR values. It has been observed that if the block size is reduced then PSNR and CR increase. The block size of 4 x 4 is most preferable. Average difference (AD) and image fidelity
IJSER @ 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 4
ISSN 2229-5518
(IF) are changing with change in PSNR values, but the change is very small.
It may not be possible that neural network technology can provide better solutions for practical image coding problems in comparison with the traditional techniques since neural network alone may require more convergence time. Therefore, future research work in image compression neural networks can be considered by the neural networks which go through more interactive training and sophisticated learning procedures. By combining wavelet theory and neural networks capability, significant improvements in the performance of the compression algorithm can be realized [20].
The Author wishes to thank Dr. Prof. Mrs. L.S. Admuthe of the Department of Electronics at the D.K.T.E’S Enggineering Institute India.
[1] Cottrell et.al. “Learning internal representation from gray-scale images: An example of extensional programming.” In Proceedings of the Ninth Conference of the Cognitive Science Society, 1987, pp 461-473.
[2] R.D. Dony, S. Haykin, “Neural network approaches to image compression”, Proc. IEEE, proc. Vol. 83, No. 2, Feb. 1995, pp 288-303.
[3] A. Namphol, S. Chin, M. Arozullah, “Image compression with a hierarchical neural network”, IEEE Trans. Aerospace Electronic Systems, Vol 32, No.1, January 1996, pp 326-337.
[4] Christophe Amerijckx et.al, “Image Compression by Self-organized Kohonen maps”, IEEE Trans. on Neural Networks,Vol.9, No.3, May 1998. [5] J. Jiang, “Image Compression with neural networks – A survey”, Signal Processing: Image communication, Elsevier Science B.V., Vol.14,
1999, pp 737-760.
[6] Antonini, M.; Barlaud, M.; Mathieu, P.; Daubechies, I, “Image coding using wavelet transform” IEEE Trans. on Image processing Vol.2
,2002,pp 205-220.
[7] S. Anna Durai, E. Anna Saro, “Image Compression with Back-
Propagation Neural Network using Cumulative Distribution Function”, International Journal for Applied Science and Engg. Technology 2006.
[8] S.S.Panda et.al, “Image compression using back propagation neural
network”, IJESAT 2012 Vol 2.
[9] Ren-Jean Liou, et.al “Quadtree Image Compression Using Sub-Band
DCT Features and Kohonen Neural Networks by” ICALIP, pp 252-256
2008.
[10] Y. Linde, A. Buzo, and R. M. Gray, “An algorithm for vector quantizer design,” IEEE Trans. Commun., vol.COMM-28, pp. 84–95, Jan.
1980.
[11]Ivan Vilovic' “An Experience in Image Compression Using Neural Networks”, 48th International Symposium ELMAR-2006, 07-09 June 2006. [12] Amjan Shaik, et.al, “Empirical Analysis of Image Compression through Wave Transform and Neural Network”. IJCSIT Vol.2, pp 924-931
2011
[13] G.Boopathy.et.al, “Implementation of Vector Quantization for Image
Compression - A Survey” Global Journal of Computer Science and
Technology Vol. 10 Issue 3 April 2010.
[14] W. K. Yeo, et. al “A Feed Forward Neural Network Compression
with Near to Lossless Image Quality and Lossy Compression Ratio”, IEEE Student Conference on Research and Development ,pp-91-94 ,Dec.2010. [15] Robina Ashraf et.al “Adaptive Architecture Neural Nets for Medical Image Compression” IEEE Proceeding, 2006.
[16] Rafael C. Gonzalez, Richard E. Woods, Digital Image Processing,
Third Edition, Pearson Education 2008.
[17] G.Boopathi,“An Image Compression Approach using Wavelet
Transform and Modified Self Organizing Map”, IJCSI International
Journal of Computer Science Issues, Vol. 8, Issue 5, No 2, September 2011.
[18] Marta Mrak, et.al “Picture quality measures in image compression systems”. EUROCON, Ljuijana, Slovenia. 2003.
[19] A.K. Krishnamurthy et al., “Neural Networks for VQ of speech and
Images”, IEEE Jl. On selected areas in comm., Vol.8, No.8, Oct 1990.
[20] Y.Dandawate et al. "Neuro-Wavelet based vector quantizer design for image compression”, Indian Journal of Science and Technology Vol.2 No.
10 Oct 2009.