Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 1
ISS N 2229-5518
Churning Multiple Communication Sources in
Cooperative Control of a Mobile Robot
Chimpalthradi R. Ashokkumar
.
—————————— ——————————
Nomenclature:
a : Op en loop sy stem matrix.
A : Closed loop system matrix.
b : Control influence matrix.
C : Communication matrix elements.
c : Interconnections
f : Feed forward control.
k : Feedback controller.
N : Number of robots engaged in the formation.
p : Position.
p : Velocity .
![]()
r : Radius of a circle for coop eration.
t : Time instants.
T : Formation matrix.
u : Control inp ut.
x : State vector.
y : Communication vector.
: Coop erative control index indicatin g velo city directions.
Subscripts:
a : Lead er.
i, j, 1, 2 : Followers.
i : Follower who gives information to its associate j.
1 : Follower who gives information to its associate 2.
j : Follower receivin g information from a and i.
2 : Follower receivin g information from a and 1.
r : Lead er or follower.
Cooperative control of multi -vehicle s ys tems has been an active res earch area in recent years [1,2]. Higher level control is gene r- ally mixed with decis ion ma king polic ies [3,4]. Various lower level control methods for multi -vehicle s ys tems are dis cuss ed in the firs t paper [5] of the s pecial is s ue [1]. So me of the control methods are demons trated experimentally [6]. Such an exerc is e for an air vehic le or a mobile robot cooperating with mu ltiple s ys tems with multip le commun ication s ources require further understanding of churning [7]. Churn ing is a co mputational o p- tion to invite data hierarchically fro m mult iple s ources and process them at the centralized or decentralized p latform o n- board a system cooperating with thos e s ystems providing the data. In this paper, a decentralized a rchitecture for leader- follower fra mework is cons idered. All the fo llo wers are as s umed to be cooperating with the leader which is ass igned to s eek a target. The leader is pro viding its informat ion to all the fo llo w- ers . In addition, one of the follower s ystems further receives
———— ——— ——— ——— ———
informat ion fro m its ass ociate. While s eeking the target, this paper develops a cooperative control algorithm and inves t igates the cooperative behavior o f the follower s ys tem that receives informat ion fro m the mu ltiple s ources . It is s hown that churning s ignificantly affects performance. Further, the initia l conditions and the direction of the velocity vectors are critica l to develop a formation with cooperation among multiple co mmun ication s ources .
In leader-follower fra mework, the informat ion flow a mong the s ys tems is shown to be process ed at the feed forward path of the repres entative systems [8,9]. Thus , a feed forward gain propo r- tional to a communication pattern is required to cooperate with the s ys tems providing the information. In doing s o, s ince the informat ion s haring among the s ystems is fro m mu ltip le s ources , it is required to cons ider a s pecific co mmun ication pattern and determine gains of the feed forward controller. Thus , various options aris e to represent the communication pattern and churn the data for a cooperative performance. In this paper, the info r- mat ion for cooperation is as sumed to be available a lternatively. Accordingly, a control alg orith m fo r the follower that receives s uch informat ion is developed to s eek a target along with the leader. Un like a s warm which s eeks a moving target [10], in order to unders tand the effects of churning on coo peration, the
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 2
ISS N 2229-5518
target is as sumed to be fixed. A lthough cooperative performance deteriorates at the expens e of data churning, the sys tem with mu ltip le communication s ources is capable of performing a ce r- tain tas k ass igned to either one of the s ys tems s haring the info r- mat ion.
The paper is organized us ing an exa mp le that enhances the t u- torial va lue. Ma inly, an interco nnection in terms of the velocity vector direction for cooperation a mong the dis tributed s ystems is dis cus sed. Then, various iss ues to process multiple co mmunic a- tions at the local control s tru cture of the s ys tem are pres ented. In decentralized platform, for a followe r with mult iple co mmunic a-
move ments in Eq. (2). The circle c rite rion is further chos en to s tudy the influence of the changing velocity directions of the follower s ys tem with res pect to the leader. Cons ider a linear time-invariant feedback controller k j and define a two-degree of freedom control law,
u j (t) k j x j (t) f j (t) . (3) The clos ed loop dynamics becomes ,
x j (t 1) Aj x j (t) b j f j
Aj (a j b j k j ) ;
p j (0)
tion s ources , an algorith m for churning the data is developed and
e xa mples are illus trated. Co nclus ions and future directions in
x j (0) p
(0)
this res earch area are s umma rized.
In leader-follower fra mework, the pos ition ( pr ) and velocity
2
Each followe r s ys tem fro m its initia l condition xr(0) is driven to origin in a certain duration of time a long with their leader. The feed forward control input fj(t) is introduced to enhance coopera- tion between the leader and its followers . Given the leader in- formation, the feed forward control proportional to the leader informat ion is applied at the follower s ys tems . However, at the
follower s ys tem xj(t), the feed forward control is proportional to
( p r ) of a finite s et of mobile robots in R
are shown in Fig.1.
the leader as well as its as sociate inputs . The objective of this
The dynamics of each robot is ass umed as an integrator. The
dis crete-time model with s amp ling one time unit is ,
paper is determine s uch a feed forward control for the follower s ys tem xj(t) s uch that the cooperative constraint in Eq. (2) is
pr (t 1) 1
1 pr (t)
0.5
(1a)
met.
ur (t)
p r (t 1)
or,
0 1 p r (t)
1
2
The cooperation given by Eq. (2) is augmented in the s ys tems as
follows . An interconnection is developed by differentiat ing Eq. (2) with res pect to time.
xr (t 1) ar xr (t) br ur (t),
xr (t) R
(1b )
pa p a
p j p j
0 pa
p j
![]()
p j
p a
(4)
pi (0)
Eq.(4) leads to xa(t) – xj(t) interconnection as follo ws ,
p3 (0) R2
p i (0)
1
c (t)
0 pa (t)
a
0 p j (t)
(5)
p 3 (0)
j
pa (0)
0 a p a (t) 0
1 p j (t)
p a (0)
Ta Tb
p j (0)
Us ing the aggregate model dis cuss ed in Ref.11 and its interco n-
nections in Eq. (5), feed forward control at the followe r s ys tem
xi(t) is applied for a=1 and a= 1, res pectively. Further, Eq.(4)
p j (0)
Fig. 1. Fo llo wer xj(t) cooperating wit xa(t) and xi(t).
Here t refe rs the time units for the dis crete time mode l taking the values 0,1, . In Figure 1, the leader is denoted by the s ub
s cript a. Cons istent with the Fig. 1, the followe rs are denoted by the subs cripts i, j and 3, res pectively. The leader or fo llower s ys tem is denoted by r[a,1, ,j,N]. Sys tems xa(t), xi(t) and xj(t) are as sumed to be in a formation to s eek a target at the ori- gin. Leader xa(t) commun icates with its followers xi(t) and xj(t)
res pectively. In addition, xi(t) also communicates with its ass o-
ciate xj(t) for further cooperation. A cooperation is cons idered by an algebraic cons traint given by,
implies that when a=1, the follower s eeks the origin by coop e- rating with its leader in s uch a way the velocity co mponents are the same in both direction and magnitude. Fig.2a and Fig.2c for various initia l conditions in firs t and third quadrants depict this s ituation, where the follower s ystem attempts to align its elf with the leader us ing a feed forward control. Thus the initial cond i- tions (15,1) and (-15,-1) a re concluded as cooperative. In the abs ence of feed forward co ntrol, it is obs erved that the follower s ys tem becomes uncooperative to both the initia l conditions . The interconnections a= 1 in Fig.2b and Fig.2d draw the s ame conclus ions . However, the formations are diffe rent with the v e-
locity vectors of the leader and follower s ystems actin g in oppo- s ite directions .
If the des ign cons traints such as the s tate and control input s at u- ration limits are impos ed, majority of the inte rconnections for
comple x maneuvers become infeas ible. Cons ider the des ign
p 2 (t) p 2 r 2
(2)
a j a
cons traints ,
That is , the follower move ments are such that at each time in- s tant they s atis fy a circ le criterion with res pect to the leader
{25 pr (t) 25, 5 p r (t) 5} .
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 3
ISS N 2229-5518
Clearly, the initia l condition (15, 1) with a=1 is cooperative with feed forward control. But it becomes invalid becaus e the maneuver is comple x. In addition, if the s ys tem begins to coop e- rate with other ass ociate following the leader, cooperative pe r- formance with init ial conditions such as (15,1) may further det e- riorate. This as pect of the s tudy is formulated ne xt.
Problem Definition : A more comp le x p roble m is pos ed as fo l-
lows . In addition to the leader to followe r co mmunicat ion, let the followe r xj(t) receives information fro m its ass ociate xi(t) s uch that,
a) xj(t) cooperates with xi(t) and
b) Both xi(t) and xj(t) cooperate with xa(t).
In this cas e, the cooperative cons traints in terms of the two alg e-
braic cons traints are,
p 2 (t) p 2 r 2 and
a j a
p 2 (t) p 2 r 2 .
fro m both is pres ented. In the following s ections , a decentralized computational platform is ass umed to s tudy the problem.
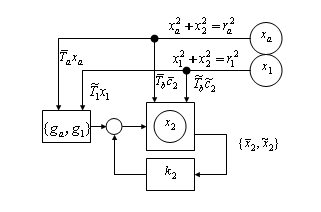
In the previous section, modeling of s patially dis tributed s ys tems with co mmunication fro m mu ltiple s ources is pres ented for a decentralized architecture. Depending upon the c ommunication s ources , a procedure to handle mult iple dyna mic mode ls pre- s ented in Eq. (9) becomes neces sary. This in turn pos es s ome computational is s ues in the feed forward path. Cons ider the fo r- mat ion of a leader xa(t) with two associates , namely x1(t) and x2(t). That is , the three systems , i =1 and j = 2 are cons idered. As a result, follower 2 receives informat ion fro m its leader xa(t) and its ass ociate x1(t). In Fig.3, a typical co mputational platform with feed back controlle r k 2 and reconfigurable feed fo rwa rd controllers {ga,g1} for the s ystem x2(t) is pres ented. The co m-
municat ions are accordingly received and process ed at the feed
i j i
Now, fo llo wer j s atis fies the follo wing t wo independent inte r- connections , one to cooperate with the leader and another to cooperate with its ass ociate,
forwa rd path.
1
0 pa (t)
a
0 p j (t)
c j (t)
p
(t)
(6)
0 a p a (t) 0
1 j
![]()
Ta
![]()
Tb
c~ t
1 0 pi (t)
i
0 p j (t)
j ( )
p
(t)
(7)
0 i p i (t) 0
1 j
~
Ta
~
Tb
![]()
![]()
![]()
Upon trans formation, the aggregate dynamics for the follower xj(t) that need to cooperate with both xa(t) and xi(t) is as follo ws : x j (t 1) Aj x j (t) xa (t) b j f j (t) , (8a)
![]()
![]()
![]()
![]()
![]()
1 1
Fig. 3. A Co mputational plat form for a fo llo wer s ystem receiv-
where,
Tb
Ta Aa AjTb
![]()
1
Ta .
ing information fro m mu ltip le co mmunication s ources .![]()
![]()
The trans formation
x j Tb
![]()
c j is with res pect to the fo rmation
![]()
matrix Tb . The leader co mmunication is denoted us ing a s tru c- tured matrix Ta . Similarly, the dynamics of xj(t) with res pect to
~
Suppos e a centralized architecture is required. The integrated
dynamics of the dis tributed s ys tems for the centralized archite c- ture is as follo ws :
its as sociate’s communication
Ti , is derived. The follower -
follower interconnection with respect to the trans fo rmation
xa (t 1)
aa 0
0 xa (t )
ba 0
0 ua (t)
~ 1
~x j Tb
c~j is given by,
x1 (t 1) 0 a1
0 x1 (t) 0 b1
0 u1 (t)
~x (t 1) A ~x (t) ~x (t) b
f (t) , (8b)
x2 (t 1)
0
0 a2 x2 (t)
0
0 b2 u2 (t)
j j j i j j
~ ~ 1 ~
~ 1 ~
(10a)
where, Tb
Ti Ai AjTb
Ti .
It can accommodate unlimited info rmation in a vector s imilar to
The feed forward controller at the followe r xj(t) with mu ltiple communicat ions becomes ,
the meas urement vector in conventional control, which is re-
ferred as a co mmunicat ion vector,
f j (t) ga (t)xa (t) (or)
Caa 0
0 xa
(t)
f j (t) gi (t)xi (t)
(9)
y(t) C1a
C
C11
C
0 x1 (t) . (10b)
C x (t)
Eq.(9) blends the information it rece ives fro m both xa(t) and
2a
21 22 2
xi(t). Accordingly, the feed forward gains
ga , gb
R12
are re-
The diagonal entries are the standard meas ured s ignals applic a-
ble for a conventional control sy stem. The off -diagonal entries
configured. Various poss ibilities do exis t to churn the data from
s ys tems xa(t) and xi(t). In the pres ence of trans mis s ion delay, the problem becomes comp le x. In order to avoid conges tion, a s im- ple procedure that accepts data from either xa(t) or xi(t) but not
indicate the communication s ources among the dis tributed s ys- tems . The triangular s tructure in Eq.(10b) has a s pecial reference to the decentralized architecture. The control law for this s pecif- ic co mmunicat ion vector will be of the fo rm,
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 4
ISS N 2229-5518
ua (t)
kaa 0
0 xa (t)
Case (a): x1(t) and x2(t) receive informat ion fro m xa(t) and coo-
perate with xa(t). This is the s tandard leader-fo llo wer control
u1 (t) k1a
k11
0 x1 (t) . (10c)
problem where each fo llo wer receives informat ion fro m s ingle
u2 (t)
k2a
k21
k22 x2 (t)
s ource, that is , the leader xa.
The output vector is given by,
c1 (t)
Ta Tb
0 xa (t)
Case (b): As in Cas e a. In addition, x2(t) begins to communicate
![]()
c (t)
![]()
0 T x
t . (10d)
with x1(t) to develop cooperation (may be to perform a d ifferent![]()
2 Ta
~ ~
1 ( )
tas k when x1(t) takes a leaders hip).
c~ (t)
0 T
T x2 (t)
Fig.5 s hows Cas e a, wherein, the followers x (t) and x (t) coope-
2 i b 2 1
Although the centralized platform is s uitable to accommodate communicat ion sources in the s tate-s pace model, it is difficu lt to synthes ize a s tructured controller as in Eq.(10c) . Fu rther, the output vector is not dimens ionally s table and its s tructure is e x- pected to vary. Thus the s tudy confines to the decentralized computing platform.
When a communicat ion delay is not pres ent, a communication pattern adopted to develop the cooperative control algorith m is s hown in Fig. 4. He re the s ystem rece iving informat ion fro m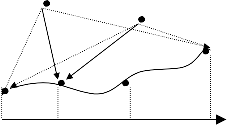
xa (t )
x1 (t )
rate with xa(t). The initial condition for each sys tem is cons i-
dered in the firs t quadrant as (10,2). The e ffect of in itia l cond i-
tions when followers are in third quadrant is illus trated in Fig. 2. The trajectories of the fo llowe rs cooperating with xa(t) s uggest that the cooperative co ntrol cons traint is s atis fied after a fin ite number of time s teps . The feed forward control input his tories (f1(t) at x1(t) and f2(t) at x2(t)) are also compared. In each of thes e s imulations , the interco nnection is defined us ing
a 1 1 . That is , the speed of each s ys tem does not exceed the s peed of the other system. In Fig.6, Cas e b is illus trated. Be- caus e x2(t) receives commun ication fro m both x1(t) and xa(t), it is trying to cooperate with both of them. Further, s a me in itia l co n- dition for each fo llo wer is as sumed. Thus , for the as sumed communicat ion pattern in Fig. 4, the type of cooperation exis ts between the s ystems x2(t) and x1(t), and between the s ys tems x2(t) and xa(t) does not change. When the initial conditions are
modified, the cooperation is s ignificantly mod ified as shown in
Sampling @ Processor
x2 (t )
t
Fig.7. As before, the interconnections are chos en us ing
a 1 1 . When multiple co mmunicat ion s ources are intro- duced, the initial cond itions s ignificantly affect the formations . The cooperative cons traints of s ys tem x2(t) with its leader xa(t)
Initial time Final time
Fig. 4. A co mmunicat ion pattern for cooperative control alg o-
and its associate x1(t) can be inferred. With the exis ting commu-
nication pattern, it is obs erved that x2(t) in Fig.7 is uncooperative to the initial condition (10,2). Although x2(t) is cooperative to
rith m
(10,2), the s peed cons traint with
a 1 1 becomes effect ive
more than one s ys tem is identified as x2(t). When informat ion fro m xa(t) is received, it is as sumed that no data fro m x1(t) is received. Thus no data conges tion occurs at s ys tem x2(t). The trans mis s ion time for this type of data trans fer is further a s- s umed twice the s ampling time of the process or at each homo- geneous s ys tem engaged in the format ion.
Als o, system x2(t) receives both pos ition and velocity informa- tion fro m xa(t) and x1(t), res pectively. The control s tructure at the feed forwa rd path is fixed as a proportional plus derivative co n- trolle r. An algorithm is developed to minimize the error b etween the leader trajectory and the followe r tra jectory. The feed fo r- ward gains for the co mmunication pattern in Fig. 4 a re acco r- dingly determined. If x2(t) makes an attempt to cooperate with
and churning occurs as it approaches the ta rget.
Control of s patially dis tributed s ys tems with mu ltip le commun i- cation s ources pres ents major challenges . This paper focus es on mu ltip le models res ulting fro m mult iple co mmun ication s ources . Unlike d is tributed s ys tems with s ingle communication s ource as in a s tandard leader-fo llo wer fra me work, when more than one communicat ion s ource is introduced, churning inevitably occurs and cooperative performance deteriorates . Us ing an a commun i- cation pattern, multip le models among the dis tributed s ys tems are us ed to develop a cooperative control algorithm. Various e xa mples with in itia l condition uncertainty are illu s trated. It is
concluded that format ion is s ens itive to initial conditions and is![]()
xa(t), then interconnection c2
becomes effective with gain ga(t).
difficult to achieve es pecially when mult iple co mmun ication
Similarly, if x2(t) ma kes an attempt to cooperate with x1(t), then
~
s ources are present. However, such sys tems can cooperate with
the interconnection c2
becomes effective with gain g1(t). The
either one of the s ystem provid ing the informat ion a nd perform
cooperative control algorith m is compared in t he fo llo wing t wo cas es :
diffe rent tas ks . Currently, churning in s warms is under inves t i-
gation.
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 5
ISS N 2229-5518
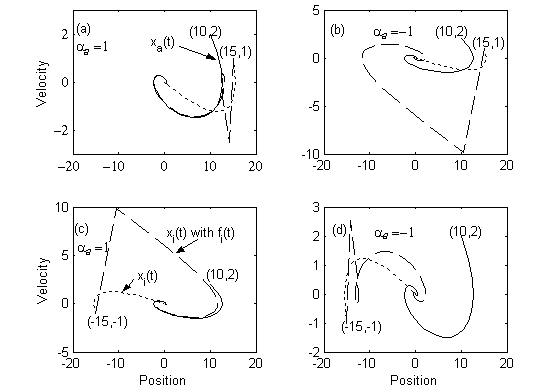
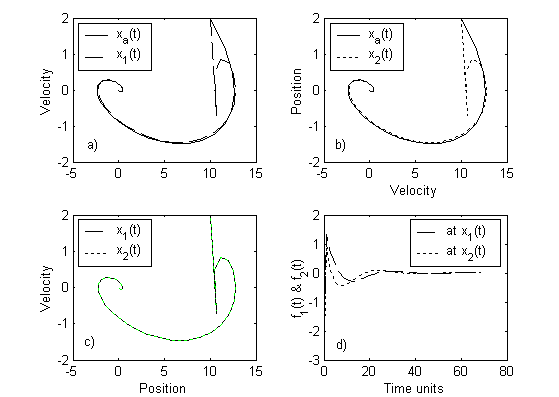
Fig. 2. Fo llo wer xi(t) cooperating with the leader xa(t)
Fig. 5. Cooperative s ys tems with s ingle co mmun ication s ource.
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 6
ISS N 2229-5518
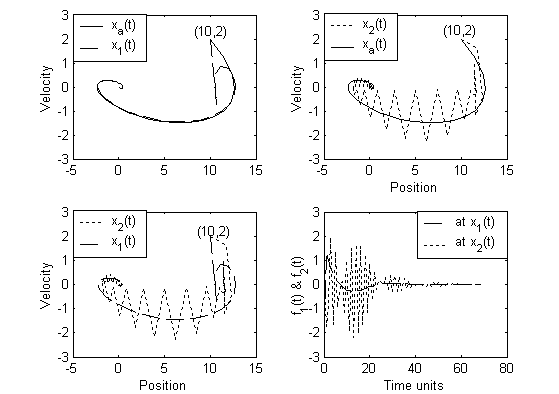
Fig. 6. Cooperative Sys tems With Multip le Co mmun ication Sources .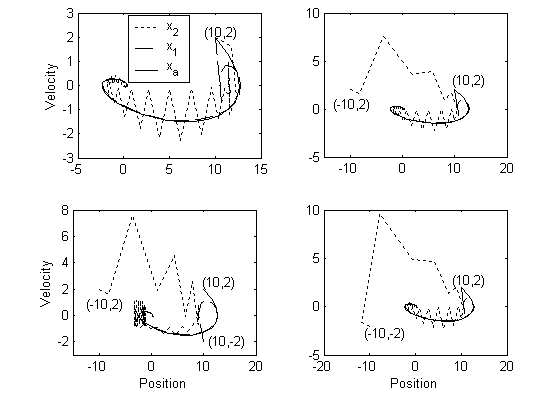
Fig. 7. In itia l Condition Effects on Cooperative Control.
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 7
ISS N 2229-5518
[1] Special Is s ue on Analys is and Control of Multi-Agent Dynamic Sys tems , Journal of Dynamic Systems, Measurement and Control, Vol 5, pp: 129, 2007.
[2] Special Is s ue on Cooperative Control Approaches for Multiple Autonomous Vehic les , International Journal of Systems Science, Vol. 37, No. 6, 2006.
[3] J. How, E. King, and Y. Ku wata, ―Flight De mons trations of Cooperative Control for UA V Tea ms ,‖ AIAA 3rd "Unmanned Unlimited" Technical Conference, Work shop and Exhibit 20 - 23 September 2004, Ch icago, Illinois , AIAA 2004-6490.
[4] G. Vachts evanos , L. Tang, G. Dro zes ki, and L. Gut ierrez,
―Intelligent Control of Unmanned Aerial Veh icles for Improved Autonomy and Relaib ility,‖ 5th IFAC/EUR ON Symposium on Intelligent Autonomous Vehicles, Instituto Superior Técn ico, Lis boa, Port ugal, July 5-7, 2004.
[5] R.M. Murray, ― Recent Res earch in Cooperative Control of
Multi-Vehic le Sys tems ,‖ Journal of Dynamic Systems, Measurement, and Control, Vo l. 129, No. 5, pp. 571-584,
2007
[6] E. King, Y. Kuwata, and J.P. How, ― Expe rimental
De mons tration of Coordinated Control of Multi-Vehic le
Teams ,‖ International Journal of Systems Science , Vol.
37, No. 6, pp. 385-398, 2006.
[7] W.J. Curt is , ―Churning: Repeated Optimization and Cooperative Ins tability,‖ In Recent Developments in Cooperative Control and Optimization . Sergiy Butenko, Robert Murphey and Panos Pardalos , Eds ., Kluver Academic Publis hers , Norwe ll, Mas s achus etts , pp: 105-
114, 2004.
[8] A.J. Fa x, and R.M. Murray, ― Graph Lap lacians and Stabilization of Vehicle Fo rmations ,‖ The 15th IFAC World Congress, June 2002.
[9] A.J. Fa x, and R.M. Murray, ―Information Flow and Cooperative Control of Veh icle Format ions ,‖ IEEE Transactions on Automatic Control, Vol. 49, No. 9, pp:
1465-1476, 2004.
[10] J. Yao, R. Ordóñez, and V. Ga zi, ― Swa rm T racking Us ing Artificia l Potentials and Sliding Mode Control,‖ Journal of Dynamic Systems, Measurement, and Control Vol. 129, No. 5, pp. 749-755, 2007.
[11] C.R. As hokku mar, and D.E. Je ffcoat, ―Cooperative
Systems Under Communication Delay,‖ AIAA Guidance, Control, and Navigation Conference, Aus tin, TX 11-13 Aug
2003.
IJSER © 2012