International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1179

ISSN 2229-5518

Chemical Reaction Effects on Heat and

Mass Transfer of Unsteady Flow over an Infinite Vertical Porous Plate Embedded in a Porous Medium with Heat Source

Dr.K.Balamurugan, Dr.S.Anuradha, Mr.R.Karthikeyan

Abstract:- The work reported herein estimates the eff ects of Chemic al reac tion on uns tead y free c on vection flow and mass transf er over an infinite vertic al porous plate whic h is embedded in porous medium with heat s ourc e. The basic governing equations of the problem ar e transf ormed into a s ystem of non dimens ional diff erential equations , whic h are then s olved an al ytic ally by us ing Perturbation tec hniques . T he dimensionless Veloc ity, temperature and c onc entration prof iles are dis played graphic ally showing the eff ec ts fluid flow f or the diff erent values of the param eters . It is interesting to note that an increas e of Grashof number,Permeability parameter and Chemic al reac tion param eter f or heat transf er acc elerates the trans ient vel oc ity of fluid.Further, it is obs erved that the temperature profile of the f luid f low decreas e while increasing of prandtl number.But increas e of permeability paramet er s hows the revers e proc ess.T he eff ect of inc reas ing Sc hmidt number is to dec reas e the c onc entration boundary layer thic kness of the f low field.Further, a growing

permeability param eter increasing the s kin friction at the wall and growing of permeability param eter (Kp≤ 1) leads to

inc reas e the magnitude of the rate of heat transf er at the wall.W hile Chemic al reac tion param eter increas e, shows th e

dec reas e eff ec ts of the rate of mass transf er at the wall.T he investigated res ults s howed graphic ally that the flow field is notably influenc ed by the c ons idering param eters .

Key words: Heat Transf er, Mass Transf er, Porous Medium, Chemic al eff ects , permeability param eter, Gras hof Number, Prandtl number, Skin fric tion.

1. Introduction

The phenomenon of hydrodynamics flow with heat and mass transfer past a porous plate
embedded in a porous medium has attracted the attention of a good number of investigators because of its varied applications in many engineering problems such as plasma studies, geothermal energy extractions and in the boundary layer control in the field of aerodynamics. The Chemical reaction plays a important role in numerous industrial applications such as polymer production, manufacturing of ceramics’ and food processing, evaporation at the surface of a water body, Generation of electricity is one in which electrical energy is extracted from the moving conducting fluid with chemical reaction plays important role in power industry. Several investigators reported such flows by involving various physical situations. Gersten K., Gross J.F. [1] discuss the nature of Flow and heat transfer along a plane wall with periodic suction. Yamamoto K.m Iwamura N[2] are studied the flow with convective acceleration through a porous medium. Bejan A and Khair K.R.[3] are deeply discussed the effects of Heat and mass transfer by natural convection in a porous medium. W.L.Cooper., V.W.Nee[4] were studied the Fluid Mechanics of oscillatory and modulated flows and associated applications in heat and mass transfer. Rapits A.A.[5] is studied the Flow through a porous medium in the presence of magnetic field. Balamurugan K.S., Varma S.V.K.,Ramakrishanaprasad K[6] deeply analyzsed the Thermo diffusion and chemical reaction effects on a three dimensional MHD Mixed convective flow along an infinite vertical porous plate with viscous and Joules dissipation.. C.Ceindreau and J.L. Auriault[7] analysed the Effect of Magnetic field on flow through porous medium. J. Prakash and A.Ogulu[8] were studied the Unsteady two dimensional flow of a radiating and chemically reacting MHD fluid wih time dependent suction Ling S.C. Nazar R., Pop.I[9] are studied the Steady mixed convection boundary layer flow over a vertical flat surface in a porous medium filled with water at 4 degree variable surface. R.Muthucumarasamy [10] is deeply discussed the Effects of heat and mass transfer on flow past an oscillatory vertical plate with variable temperature. R.Muthucumarasamy and B.Janakiraman [11] are studied the Mass transfer effects on isothermal vertical oscillating plate in the presence of chemical reaction. M.C.Raju,S.V.K. Verma, P.V.Reddy and S.Saha[12] analyzed the Soret Effect due to Natural convection between heated inclined plates with magnetic field. Balamuguran K.S., Varma S.V.K. and Iyengar N.ch.S.N [13] discussed the nature of the Chemcial reaction and thermo diffusion effects on MHD three dimensional free convection coquette flow with Heat Absorpton. N.Senapati and R.K.Dhal [14] discussed the nature of the Magnetic effect on mass and heat transfer of hydrodynamic flow past a vertical oscillating plate in the presence of chemical reaction.S.S. Das (et.al) [15] discussed the combined natural convection and mass transfer effects on unsteady flow past an infinite vertical

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1180

ISSN 2229-5518

porous plate embedded in a porous medium with heat source.

2. Formulation of the Problem

Considered a unsteady natural convective heat and mass transfer flow of a viscous incompressible fluid past an infinite vertical porous plate which is embedded in porous medium with heat source. The x’ axis is taken in vertically upward direction along the plate and y’ axis is chosen normal to it. Neglecting the Joulean heat dissipation and applying Boussinesq’s approximation the governing equations of the flow field are written as follows:

Continuity Equation:

′

∂y′ = 0 ; v

= −v′0 (Constant) (1)

Momentum Equation:

𝝏 𝒖

′ 𝝏𝒖′

𝝏 𝒖

′ ′ ∗ ′

′ 𝒗 ′

𝝏𝒕′ + 𝒗 𝝏𝒚′ = 𝒗 𝝏𝒚′𝟐 + 𝒈𝜷(𝑻 − 𝑻∞ ) + 𝒈𝜷

(𝑪

− 𝑪∞ ) − 𝑲′ 𝒖

(2)

Energy Equation:

′ ′ 𝟐 ′

′ 𝟐

𝒖′ 𝝏𝑻

+ 𝒗′ 𝝏𝑻

𝝏 𝑻

+ 𝝑

𝝏𝒖 �

+ 𝑺′ (𝑻′ − 𝑻

′ ) (3)

𝝏𝒕′

𝝏𝒚′ = 𝒌 𝝏𝒚′ 𝟐

𝑪𝒑 𝝏𝒚′ ∞

Concentration Equation:

𝝏 𝑪

′ 𝝏𝑪′

𝝏 𝑪 ′ ′

𝝏𝒕′ + 𝒗 𝝏𝒚′ = 𝑫 𝝏𝒚′𝟐 − 𝑲𝒓′(𝑪 − 𝑪∞ ) (4)

Boundary Conditions of the problem are:

′ ′ ′ ′

𝑢′ = 𝟎, 𝒗′ = −𝒗𝟎 ′ , 𝑻′ = 𝑻𝒘 ′ + 𝜺(𝑇𝒘 ′ − 𝑻∞ ′ )𝒆𝒊𝝎 𝒕 , 𝑪′ = 𝑪𝒘 ′ + 𝜺(𝐶𝒘 ′ − 𝐶∞ ′ )𝒆𝒊𝝎 𝒕

𝒂𝒕 𝑦′ = 𝟎

𝑢′ → 𝟎, 𝑻′ → 𝑻∞ ′ , 𝑪′ → 𝑪∞ ′ 𝒂𝒔 𝒚′ → ∞ (5)

Now, Introducing the following non- dimensional variables and parameters.

′ ′ ′ ′ 𝟐 ′ ′

′ 𝟐𝑲′ ′ ′ ′ ′

𝒚 = 𝒚 𝒗 𝟎 , 𝒕 = 𝒕 𝒗 𝟎 , 𝝎 = 𝟒𝝑𝝎 , 𝒖 = 𝒖

, 𝝑 = 𝜼𝟎 , 𝐾

= 𝒗 𝟎

,𝑇 = 𝑻 −𝑻∞

, 𝐶 = 𝑪 −𝑪∞

𝑃 = 𝝑,

𝝑 𝟒𝝑

𝒗′𝟎𝟐

𝒗′𝟎

𝝆 𝑝

𝝑𝟐

𝑻′𝒘−𝑻∞ ′

𝑪𝒘′−𝑪∞ ′ 𝒓 𝒌

′ ′ ′ ′

′ ′ 𝟐 ′

𝐺𝑟 = 𝜗𝑔𝛽 (𝑻 𝒘−𝑻∞ ) , 𝐺𝑐 = 𝜗𝑔𝛽(𝑻 𝒘−𝑻∞ ) , 𝑆𝑐 = 𝜗 , 𝑆 = 4𝑆 𝜗, 𝐸𝑐 = 𝒗 𝟎 , K = K ϑ

(6)

𝑣 ′03

𝐷 𝒗′ 𝟎𝟐

𝑪𝒑(𝑻′

𝒘−𝑻∞ ′) r

ϑ0 2

Where g , ρ, ϑ, β, β∗ ,ω, η0,k, T ′, T ′w , T ′∞ , C′, Cw ′ , C∞ ′, Cp, D, Pr, Sc, Gr, Gc, S, Kp , Ec and Kr are respectively the
acceleration due to gravity, density, coefficient of kinematic viscosity, volumetric coefficient of expansions for
heat transfer,volumetric coefficient of expansions for mass transfer, angular frequency,Coefficient of viscosity, thermal diffusivity, temperature, temperature at the plate, temperature at infinity,Concentration, Concentration at the plate, concentration at infinity, specific heat at constant pressure,molecular mass diffusivity,Prandtl number,Schmidt number, Grashof number for heat transfer, Grahof number for mass transfer, heat source parameter, permeability parameter, Eckert number and Chemical reaction parameter.
Substituting equation (6) in equations (2),(3), and (4) under boundary conditions (5) we get

1 𝜕𝑢 − 𝜕𝑢 = 𝜕 𝑢 + 𝐺𝑟𝑇 + 𝐺𝑐 − 1

𝑢 (7)

4 𝜕𝑡

𝜕𝑦

𝜕𝑦2

𝐾𝑝

1 𝜕𝑇 − 𝜕𝑇 = 1 𝜕2 𝑇 + 1

𝜕𝑢�

(8)

4 𝜕𝑡

𝜕𝑦

𝑃𝑟 𝜕𝑦2

𝑆𝑇 + 𝐸𝑐 �

4 𝜕𝑦

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1181

ISSN 2229-5518

1 𝜕𝐶 − 𝜕𝐶 = 1 𝜕2 𝐶

4 𝜕𝑡

𝜕𝑦

𝑆𝑐 𝜕𝑦2 − 𝐾𝑟𝑐 (9)

The Corresponding boundary conditions are:

𝑢 = 0, 𝑇 = 1 + 𝜀𝑒𝑖𝜔𝑡 , 𝐶 = 1 + 𝜀𝑒𝑖𝜔𝑡 𝑎𝑡 𝑦 = 0

𝑢 → 0, 𝑇 → 0, 𝐶 → 0 𝑎𝑠 𝑦 → ∞ (10)

3. Method of Solution
To solve equations (7), (8) and (9) , Assuming ε to be small so that one can express u, T and Cas a regular perturbation series interms ε as in the neighborhood of the plate as

𝑢(𝑦, 𝑡) = 𝑢0 (𝑦) + 𝜀𝑒𝑖𝜔𝑡 𝑢1 (𝑦) + 𝑂(𝜀2 ) (11)

𝑇(𝑦, 𝑡) = 𝑇0 (𝑦) + 𝜀𝑒𝑖𝜔𝑡 𝑇1 (𝑦) + 𝑂(𝜀2 ) (12)

𝐶(𝑦, 𝑡) = 𝐶0 (𝑦) + 𝜀𝑒𝑖𝜔𝑡 𝐶1 (𝑦) (13)

Substituting equations (11) – (13) in equations (7) –(9) respectively, equating harmonic and nonharmonic terms
and the neglecting the coefficients of ε2 then we get

𝑢0 ′′ + 𝑢0 ′ −

𝐾𝑝

𝑢0 = −𝐺𝑟𝑇0 − 𝐺𝑐𝐶0 (14)

𝑇0 ′′ + 𝑃𝑟𝑇0 ′ +

𝑃𝑟𝑆

𝑇0 = −𝑃𝑟𝐸𝑐 �

𝜕𝑢0 �2

𝜕𝑦

(15)

𝐶0 ′′ + 𝑆𝑐𝐶0 ′ − 𝑆𝑐𝐾𝑟 𝐶0 = 0 (16)

First Order:

𝑢1 ′′ + 𝑢1 ′ − �

𝑖𝜔

+ 1

𝐾𝑝

� 𝑢1 = −𝐺𝑟𝑇1 − 𝐺𝑐𝐶1 (17)

𝑇1 ′′ + 𝑃𝑟𝑇1 ′ −

𝑃𝑟

(𝑖𝜔 − 𝑆)𝑇1 = −2𝑃𝑟𝐸𝑐 �

𝜕𝑢0

𝜕𝑦

� �𝜕𝑢1

𝜕𝑦

� (18)

𝐶1 ′′ + 𝑆𝑐𝐶1 ′ − 𝑆𝑐 �

𝑖𝜔

+ 𝐾𝑟 � 𝐶1 = 0 (19)

The Corresponding boundary conditions are

𝑦 = 0: 𝑢0 = 0, 𝑇0 = 1, 𝐶0 = 1, 𝑢1 = 0, 𝑇1 = 1, 𝐶1 = 1

𝑦 → ∞: 𝑢0 = 0, 𝑇0 = 0, 𝐶0 = 0, 𝑢1 = 0, 𝑇1 = 0, 𝐶1 = 0 (20)

Solving equations (16) & (19) under the boundary condition (20), then we get

𝐶0 = 𝑒𝑀2 𝑦 (21)

𝐶1 = 𝑒 𝑀4 𝑦 (22)

Using Multi parameter perturbation technique and assuming Ec≪ 1, we take

𝑢0 (𝑦) = 𝑢00 (𝑦) + 𝐸𝑐𝑢01 (23)

𝑇0 = 𝑇00 + 𝐸𝑐𝑇01 (24)

𝑢1 = 𝑢10 + 𝐸𝑐𝑢11 (25)

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1182

ISSN 2229-5518

𝑇1 = 𝑇10 + 𝐸𝑐𝑇11 (26)

Now using equations (23) –(26) in equations (14),(15),(17) and (18) and equating the coefficients of like powers
of Ec neglecting of Ec 2, we get the following set of differential equations

Zeroth Order:

𝑢00 ′′ + 𝑢00 ′ − �

𝐾𝑝

� 𝑢00 = −𝐺𝑟𝑇00 − 𝐺𝑐𝐶0 (27)

𝑢10 ′′ + 𝑢10 ′ − �

𝑖𝜔 +

𝐾𝑝

� 𝑢10 = −𝐺𝑟𝑇10 − 𝐺𝑐𝐶1 (28)

𝑇00 ′′ + 𝑃𝑟𝑇00 ′ +

𝑃𝑟𝑆

𝑇00 = 0 (29)

𝑇10 ′′ + 𝑃𝑟𝑇10 ′ −

𝑃𝑟

(𝑖𝜔 − 𝑆)𝑇10 = 0 (30)

The Corresponding boundary conditions are

𝑦 = 0: 𝑢00 = 0, 𝑇00 = 1, 𝑈10 = 0, 𝑇10 = 1

𝑦 → ∞: 𝑢00 = 0, 𝑇00 = 0, 𝑈10 = 0, 𝑇10 = 1 (31)

First Order:

𝑢01 ′′ + 𝑢01 ′ − �

𝐾𝑝

� 𝑢01 = −𝐺𝑟𝑇01 (32)

𝑢11 ′′ + 𝑢11 ′ − �

𝑖𝜔 +

𝐾𝑝

� 𝑢11 = −𝐺𝑟𝑇11 (33)

𝑇01 ′′ + 𝑃𝑟𝑇01 ′ +

𝑃𝑟𝑆

𝑇01 = −𝑃𝑟(𝑢00 ′ )2 (34)

𝑇11 ′′ + 𝑃𝑟𝑇11 ′ −

𝑃𝑟

(𝑖𝜔 − 𝑆)𝑇11 = −2𝑃𝑟 �

𝜕𝑢00

𝜕𝑦

� �𝜕𝑢10

𝜕𝑦

� (35)

The Corresponding boundary conditions become,

𝑦 = 0: 𝑢01 = 0, 𝑇01 = 0, 𝑢11 = 0, 𝑇11 = 0

𝑦 → ∞: 𝑢01 = 0, 𝑇01 = 0, 𝑢11 = 0, 𝑇11 = 0 (36)

Solving equations (27)-(30) subject to the boundary conditions (31) we get

𝑢00 = 𝐴10 𝑒𝑀10 𝑦 + 𝐴11 𝑒 𝑀6 𝑦 + 𝐴12 𝑒𝑀2 𝑦 (37)

𝑇00 = 𝑒𝑀6 𝑦 (38)

𝑢10 = 𝐴14 𝑒𝑀12 𝑦 + 𝐴15 𝑒𝑀8 𝑦 + 𝐴16 𝑒𝑀4 𝑦 (39)

𝑇10 = 𝑒 𝑀8 𝑦 (40)

Solving equations (32)-(35) subject to boundary conditions (36) we get

𝑇01 = 𝐴18 𝑒𝑀14𝑦 + 𝐵1 𝑒2𝑀10𝑦 + 𝐵2 𝑒2𝑀6𝑦 + 𝐵3 𝑒2𝑀2𝑦 + 𝐵4 𝑒(𝑀6+𝑀10)𝑦 + 𝐵5 𝑒(𝑀1+𝑀6 )𝑦 + 𝐵6 𝑒(𝑀2 +𝑀10 )𝑦 (41)

𝑇11 = 𝐴20 𝑒𝑀16𝑦 + 𝐶1 𝑒(𝑀10+𝑀12 )𝑦 + 𝐶2 𝑒(𝑀8+𝑀10)𝑦 + 𝐶3 𝑒(𝑀4+𝑀10)𝑦 + 𝐶4 𝑒(𝑀6+𝑀12)𝑦 + 𝐶5 𝑒(𝑀6+𝑀8)𝑦 + 𝐶6 𝑒(𝑀4+𝑀6)𝑦

+ 𝐶7 𝑒(𝑀2+𝑀12)𝑦 + 𝐶8 𝑒(𝑀2+𝑀8)𝑦 + 𝐶9 𝑒(𝑀2+𝑀4)𝑦 (42)

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1183

ISSN 2229-5518

𝑢01 = 𝐴22 𝑒𝑀18𝑦 + 𝐷1 𝑒𝑀14𝑦 + 𝐷2 𝑒2𝑀10𝑦 + 𝐷3 𝑒2𝑀2𝑦 + 𝐷4 𝑒(𝑀6+𝑀10)𝑦 + 𝐷5 𝑒(𝑀2+𝑀6)𝑦 + 𝐷6 𝑒(𝑀2+𝑀10)𝑦

+ 𝐷7 𝑒2𝑀6𝑦 (43)

𝑢11 = 𝐴24 𝑒𝑀20𝑦 + 𝐸1 𝑒𝑀16𝑦 + 𝐸2 𝑒(𝑀10+𝑀12)𝑦 + 𝐸3 𝑒(𝑀8+𝑀10)𝑦 + 𝐸4 𝑒(𝑀4+𝑀10)𝑦 + 𝐸5 𝑒(𝑀6+𝑀12)𝑦 + 𝐸6 𝑒(𝑀6+𝑀8)𝑦

+ 𝐸7 𝑒(𝑀4+𝑀6)𝑦 + 𝐸8 𝑒(𝑀2+𝑀12)𝑦 + 𝐸9 𝑒(𝑀2+𝑀8)𝑦 + 𝐸10 𝑒(𝑀2+𝑀4)𝑦 (44)

Substituting the values of C0 and C1 from equations(21) and (22) in equation(13) the solution for concentration distribution of the flow field is given by

C== 𝑒𝑀2𝑦 + 𝜖𝑒𝑖𝜔𝑡+𝑀4𝑦 (45)

3.1 Skin friction: The wall shear stress i.e. the skin friction at the wall is given by

𝜏 𝜕𝑢

𝑤= � �

= A10M10 +A11 M6 +A12M2 +Ec(A22 M10 +D1M6 +2D2M10 +2D3M2 +(M6 +M10 )D4+(M6 +M2 )D5+(M10 +M2 )D6 +2M6D7)+𝜖Exp[𝐼𝜔𝑡](A14 M12 +A18 M87 +A16M4 +

𝜕𝑦 𝑦=0

𝜖Exp[𝐼𝜔𝑡]Ec�A24M12 +E1M8 +E2 (M10 +M12 )+E3 (M10 +M8 )+E4 (M4 +M6)+E5(M6 +M12 )+E6 (M8 +M6 )+E7(M6 +M4)+E8 (M2 +M12 )+E9 (M2 +M8)+E10 (M2 +M4)�

3.2 Heat flux: The rate of heat transfer i.e heat flux at the wall in terms of Nusselt Number Nu is given by

𝜕𝑇

𝑁𝑢 = � �

𝜕𝑦 𝑦=0

= M6 + Ec(A18M6 + 2B1M10 + 2B2M6 + 2B3M2 + B4(M6 + M10) + B5(M6 + M2) + B6(M2 + M10)) + 𝜖Exp[𝐼𝜔𝑡](M8Ec(A20M8 + C1 (M10

+ M12 ) + C2(M10 + M8) + C3(M4 + M10 ) + C4 (M6 + M12) + C5 (M6 + M8) + C6(M6 + M4) + C7 (M2 + M12) + C8 (M2 + M8) + C9 (M2

+ M4)))

3.3 Mass flux: The rate of Mass transfer i.e. mass flux at the wall in terms of Sherwood Number Sh is given by

𝜕𝐶

𝑆ℎ = � �

= 𝑀2 + 𝑀4𝜖Exp[𝐼𝜔𝑡]

𝜕𝑦 𝑦=0

4.Results and discussions:-

The effects of Chemical reaction parameter in heat and mass transfer on unsteady flow of a
viscous incompressible fluid past an infinite vertical porous plate embedded in a porous medium with heat
source has been studied. The effects of parameters in the fluid flow are thoroughly analyzed and given in the
form of graph to easily understand. The figure 1-5 shown velocity profile, 6,7 & 8 shown temperature profile
and 9 and 10 shown concentration profile.

Velocity field: The flow parameters affecting the velocity flow field are permeability parameter Kp., Grashof

number for both heat and mass transfer Gr, Gc, Schmidt Number Sc, Chemical reaction parameter Kr and Heat
source parameter s the accelerate affects on the transient velocity of the flow field while Increasing effects of
Grahsof number Gr, Grahsof number Gc, as shown in the figures 1,2 as well as inverse effects exists in the
transient velocity of the flow field while increasing Chemical Parameter(Kr)(i.e shows decrease effects the
velocity of the flow field in the figure .3). But increasing of Permeability parameter Kp and Heat source S
accelerate the transient velocity of the fluid flow as shown in the figure 4 and 5.

Temperature Field: Temperature profiles of the flow field with the effected parameters like Prandtl number, Grahsof number Gr are graphically shown its effects on the flow field. In the figures 6,7 indicates temperature profile goes on decrease while growing parameter Prandtl Number Pr and Grahsof number Gr .As well as figure 8 shown the increasing effects of temperature profile while growing parameter of heat source S

Concentration Field: Schmidt Number and Chemical reaction parameter plays important role in the concentration fluid flow field. The effects of these parameters on the fluid flow field graphically shown. While growing Schmidt number (Sc) decrease the concentration boundary layer thickness of the flow in similar way the effects of mass transfer are decrease while growing of Chemical reaction parameter (Kr)as shown in the

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1184

ISSN 2229-5518

figure 9 and figure 10.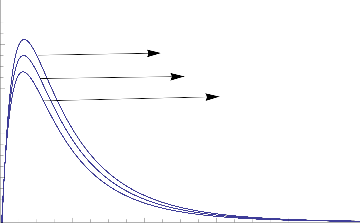

1.0
0.8
0.6
Gr =6
Gr =5
Gr =4
0.4
0.2
0.0
0 2 4 6 8 10
Fig.1 Transient Velocity for various values of Gr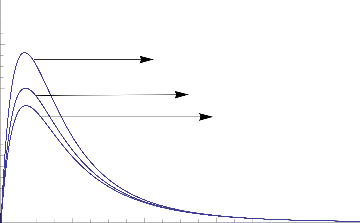

1.0
0.8
0.6
0.4
Gc=5
Gc= 3
Gc=2
0.2
0.0
0 2 4 6 8 10
Fig.2 Transient Velocity for various values of Gc

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1185

ISSN 2229-5518

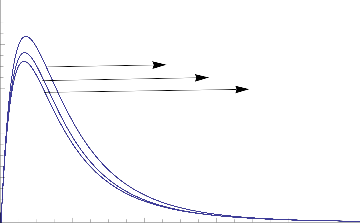
1.0
0.8
0.6
K=0.05
K= 0.35
K=0.65
0.4
0.2
0.0
0 2 4 6 8 10
Fig.3 Transient Velocity for various values of K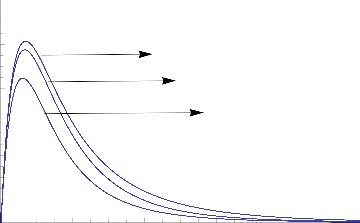

1.0
0.8
0.6
0.4
S=0.65
S=0.45
S=0.25
0.2
0.0
0 2 4 6 8 10
1.0

Fig.4 Transient Velocity for various values of S
0.8
Kp=0.25
0.6
Kp =0.15
0.4
0.2
Kp =0.05
0.0
0 2 4 6 8 10
Fig.5 Transient Velocity for various values of Kp

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1186

ISSN 2229-5518

1.0
0.8
0.6
Pr=0.71
0.4
Pr=5
0.2
Pr=7
0.0
0 2 4 6 8 10
Fig.6 Temperature Distribution for various values of Pr

1.0
0.8
0.6
0.4
Gr=15
Gr=20
Gr=25
0.2
0.0
0 2 4 6 8 10
1.0
Fig.7 Temperature Distribution for various values of Gr

0.8
0.6
0.4
S=0.65
S=0.51
S=0.25
0.2
0.0
0 2 4 6 8 10
Fig.8 Temperature Distribution for various values of S

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1187

ISSN 2229-5518

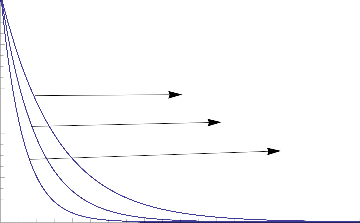
1.0
0.8
0.6
Sc=0.25
0.4
Sc=0.5
Sc=1.0
0.2
0.0
0 2 4 6 8 10
Fig.9 Concentration Distribution for various values of Sc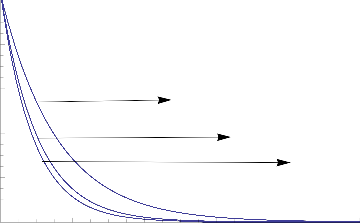

1.0
0.8
0.6
K=1.0
0.4
K=2.75
0.2
K=3.75
0.0
0 2 4 6 8 10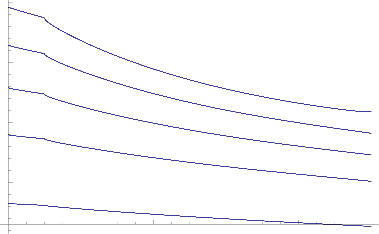

3.0
Fig.10 Concentration Distribution for various values of Kr
2.5
Kp=0.5
Kp=0.4
2.0
Kp=0.3
Kp=0.2
1.5
Kp=0.1
0.2 0.4 0.6 0.8 1.0
Fig.11 Skin friction for various values of Kp

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1188

ISSN 2229-5518

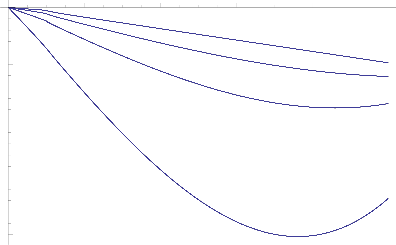
0.2 0.4 0.6 0.8 1.0

Kp=0.1

1 Kp=2.0

Kp=2.5

2

3

Kp=3.0

4

Fig.12 Heat Flux against various values of Kp

0.2 0.4 0.6 0.8 1.0

0.5

1.0

Kr=0.5

Kr=1.5

1.5

Kr=2.5

2.0

Kr=3.5

2.5

5.Conclusion

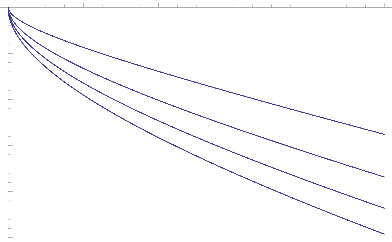
Fig.13 Mass Flux for various values of Kr
In this paper clearly shows effects of the parameters in the flow fluid. The velocity,
temperature and concentration profiles are shown graphically with various values of parameters.
Permeability parameter(Kp) accelerates the transient velocity for the small values of (Kp<1) but growing values
of Kp shows the reverse effects.
Growing of Grashof Number (Gr) accelerates the transient velocity of the fluid flow but growing Chemical
reaction parameter(Kr) retards the transient velocity.Permeability parameter (Kp) accelerates the temperature
profile of the fluid flow, but the reverse process exists if the growing parameter of Prandtl number.
The parameter of Chemical reaction (Kr) retards the concentration of mass while grown.The same effects exists in the concentration of mass while increasing of Schmidt Number(Sc)
The variation of skin friction at the wall against the different values of permeability parameter (Kp) and
Prandtl number (Pr) are shown in Fig.11.It observed the growing permeability parameter and Prandtl number
shows increasing effects of skin friction.
The rate of heat transfer at the wall for the different values of Prandtl number (Pr) and permeability parameter
(Kp) are shown in Fig.12. It is noted that the enchance of heat transfer while increasing effects of heat transfer
for Prandtl number and (Kp ≤ 1) but the reverse process of heat transfer exists while (Kp > 1)
While the rate of mass transfer at the wall decrease when increasing values of Schmidt Number (Sc) and
Chemical reaction parameter (Kr)

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1189

ISSN 2229-5518

Appendix:-

−𝑆𝑐 − �𝑆𝑐2 + 4𝑆𝑐𝐾𝑟

𝑀2 =

𝑀4 =

𝑀6 =

𝑀8 =

−𝑆𝑐 − �𝑆𝑐2 + 𝑆𝑐(4𝐾𝑟 + 𝑖𝜔)

−𝑃𝑟 − √𝑃𝑟2 − 𝑃𝑟𝑠

−𝑃𝑟 − �𝑃𝑟2 + Pr(𝑖𝜔 − 𝑠)

= −1 − �1 + 4

𝐾𝑝

𝑀10

−1−�1+ 4 +𝑖𝜔

𝐾𝑝

𝑀12 = 2

𝐴5 + 𝐴6 = 1 ,

−𝐺𝑟

𝐴11 =

𝑀6 2 + 𝑀6 −

𝐾𝑝

𝐴12 =

−𝐺𝑐

𝑀2 2 + 𝑀2 −

𝐾𝑝

𝐴10 = −(𝐴11 + 𝐴12 )

−𝐺𝑟

𝐴15 =

𝑖𝜔

𝑀 2 + 𝑀 − ( + )

𝐾𝑝 4

𝐴16 =

−𝐺𝑐

𝑖𝜔

𝑀 2 + 𝑀 − ( + )

𝐾𝑝 4

𝐴14 = −(𝐴15 + 𝐴16 )

𝐴18 = −(𝐵1 + 𝐵2 + 𝐵3 + 𝐵4 + 𝐵5 + 𝐵6 )

−𝑃𝑟𝑀10 2 𝐴10 2

𝐵1 =

4𝑀10 2 + 2𝑃𝑟𝑀10 +

𝑃𝑟𝑠

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1190

ISSN 2229-5518

−𝑃𝑟𝑀6 2 𝐴11 2

𝐵2 =

𝐵3 =

4𝑀6 2 + 2𝑃𝑟𝑀6 +

−𝑃𝑟𝑀2 2 𝐴12 2

4𝑀2 2 + 2𝑃𝑟𝑀2 +

𝑃𝑟𝑠

𝐵4 =

−2𝑃𝑟𝑀10 𝐴10 𝑀6 𝐴11

(𝑀6 + 𝑀10 )2 + 𝑃𝑟(𝑀6 + 𝑀10 ) +

−2𝑃𝑟𝑀2 𝐴12 𝑀6 𝐴11

𝑃𝑟𝑠

𝐵5 =

𝐵6 =

(𝑀6 + 𝑀2 )2 + 𝑃𝑟(𝑀6 + 𝑀2 ) +

−2𝑃𝑟𝑀2 𝐴10 𝑀10 𝐴12

𝑃𝑟𝑠

(𝑀10 + 𝑀2 )2 + 𝑃𝑟(𝑀10 + 𝑀2 ) + 4

𝐴20 = −(𝐶1 + 𝐶2 + 𝐶3 + 𝐶4 + 𝐶5 + 𝐶6 + 𝐶7 + 𝐶8 + 𝐶9 )

−2𝑃𝑟𝑀12 𝐴10 𝑀10 𝐴14

𝐶1 =

(𝑀10 + 𝑀12 )2 + 𝑃𝑟(𝑀10 + 𝑀12 ) −

−2𝑃𝑟𝑀8 𝐴10 𝑀10 𝐴15

𝑃𝑟 (𝑖𝜔 − 𝑠)

𝐶2 =

(𝑀10 + 𝑀8 )2 + 𝑃𝑟(𝑀10 + 𝑀8 ) −

−2𝑃𝑟𝑀4 𝐴10 𝑀10 𝐴16

𝑃𝑟 (𝑖𝜔 − 𝑠)

𝐶3 =

𝐶4 =

(𝑀10 + 𝑀4 )2 + 𝑃𝑟(𝑀10 + 𝑀4 ) −

−2𝑃𝑟𝑀6 𝐴11 𝑀12 𝐴14

(𝑀6 + 𝑀12 )2 + 𝑃𝑟(𝑀6 + 𝑀12 ) −

−2𝑃𝑟𝑀6 𝐴11 𝑀8 𝐴15

𝑃𝑟 (𝑖𝜔 − 𝑠)

𝐶5 =

𝐶6 =

(𝑀6 + 𝑀8 )2 + 𝑃𝑟(𝑀6 + 𝑀8 ) −

−2𝑃𝑟𝑀6 𝐴11 𝑀4 𝐴16

(𝑀6 + 𝑀4 )2 + 𝑃𝑟(𝑀6 + 𝑀4 ) −

𝑃𝑟 (𝑖𝜔 − 𝑠)

𝐶7 =

−2𝑃𝑟𝑀2 𝐴12 𝑀12 𝐴14

(𝑀2 + 𝑀12 )2 + 𝑃𝑟(𝑀2 + 𝑀12 ) −

−2𝑃𝑟𝑀2 𝐴12 𝑀8 𝐴15

𝑃𝑟 (𝑖𝜔 − 𝑠)

𝐶8 =

(𝑀2 + 𝑀8 )2 + 𝑃𝑟(𝑀2 + 𝑀8 ) −

𝑃𝑟 (𝑖𝜔 − 𝑠)

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1191

ISSN 2229-5518

𝐶9 =

−2𝑃𝑟𝑀2 𝐴12 𝑀4 𝐴16

(𝑀2 + 𝑀4 )2 + 𝑃𝑟(𝑀2 + 𝑀4 ) −

𝑃𝑟

4 (𝑖𝜔 − 𝑠)

𝐴22 = −(𝐷1 + 𝐷2 + 𝐷3 + 𝐷4 + 𝐷5 + 𝐷6 + 𝐷7 )

−𝐺𝑟𝐴18

𝐷1 =

𝑀6 2 + 𝑀6 −

𝐾𝑝

𝐷2 =

−𝐺𝑟𝐵1

4𝑀10 2 + 2𝑀10 −

−𝐺𝑟𝐵2

𝐾𝑝

𝐷3 =

4𝑀6 2 + 2𝑀6 −

−𝐺𝑟𝐵3

𝐾𝑝

𝐷4 =

4𝑀2 2 + 𝑀2 −

𝐾𝑝

𝐷5 =

−𝐺𝑟𝐵4

𝐷6 =

𝐷7 =

(𝑀6 + 𝑀10 )2 + (𝑀6 + 𝑀10 ) − 𝐾𝑝

−𝐺𝑟𝐵5

(𝑀 + 𝑀 )2 + (𝑀 + 𝑀 ) − 1

−𝐺𝑟𝐵6

(𝑀 + 𝑀 )2 + (𝑀 + 𝑀 ) − 1

𝐴24 = −(𝐸1 + 𝐸2 + 𝐸3 + 𝐸4 + 𝐸5 + 𝐸6 + 𝐸7 + 𝐸8 + 𝐸9 + 𝐸10 )

−𝐺𝑟𝐴20

𝐸1 =

𝑀8 2 + 𝑀8 − �

𝐾𝑝 +

𝑖𝜔

4 �

𝐸2 =

−𝐺𝑟𝐶1

𝑖𝜔

(𝑀10+ 𝑀12 )2 + (𝑀10+ 𝑀12 ) − �𝐾𝑝 + 4 �

−𝐺𝑟𝐶2

𝐸3 =

𝐸4 =

(𝑀 𝑀 )2 + (𝑀 𝑀 ) − � 1 +

𝐾𝑝

−𝐺𝑟𝐶3

(𝑀 𝑀 )2 + (𝑀 𝑀 ) − � 1 +

𝐾𝑝

𝑖𝜔

4 �

𝑖𝜔

4 �

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1192

ISSN 2229-5518

𝐸5 =

−𝐺𝑟𝐶4

𝑖𝜔

(𝑀12+ 𝑀6 )2 + (𝑀12+ 𝑀6 ) − �𝐾𝑝 + 4 �

−𝐺𝑟𝐶5

𝐸6 =

𝐸7 =

𝐸8 =

(𝑀 𝑀 )2 + (𝑀 𝑀 ) − � 1 +

𝐾𝑝

−𝐺𝑟𝐶6

(𝑀 𝑀 )2 + (𝑀 𝑀 ) − � 1 +

𝐾𝑝

−𝐺𝑟𝐶7

𝑖𝜔

4 �

𝑖𝜔

4 �

𝑖𝜔

(𝑀12+ 𝑀2 )2 + (𝑀12+ 𝑀2 ) − �𝐾𝑝 + 4 �

−𝐺𝑟𝐶8

𝐸9 =

(𝑀 𝑀 )2 + (𝑀 𝑀 ) − � 1 +

𝐾𝑝

−𝐺𝑟𝐶9

𝑖𝜔

4 �

𝐸10 =

(𝑀 𝑀 )2 + (𝑀 𝑀 ) − � 1 +

𝐾𝑝

𝑖𝜔

4 �

International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 1193

ISSN 2229-5518

Reference:

[1]Gersten K., Gross J.F. “Flow and heat transfer along a plane wall with periodic suction”.Z.Angew
Math.Phys.1974,25,399-408.
[2]Yamamoto K.m Iwamura N. “Flow with convective acceleration through a porous medium”.Engineering
Math.1976,10,41-54.
[3] Bejan A and Khair K.R. “Heat and mass transfer by natural convection in a porous medium”. International
Journal of Heat and Mass Transfer.1985,28,909-918.
[4]W.L.Cooper., V.W.Nee. “Fluid Mechanics of oscillatory and modulated flows and associated applications in
heat and mass transfer”. Journal of Energy Heat and Mass Transfer. 1993,15,1-19.
[5] Rapits A.A., “Flow through a porous medium in the presence of magnetic field”.International Journal of
Energy.1986,10,97-100.
[6] Balamurugan K.S., Varma S.V.K.,Ramakrishanaprasad K. “Thermo diffusion and chemical reaction effects
on a three dimensional MHD Mixed convective flow along an infinite vertical porous plate with viscous and
Joules dissipation”. International Journal of Advances in Science and Technology.2001.3,73-92.
[7]C.Ceindreau and J.L. Auriault. “Effect of Magnetic field on flow through porous medium”.Journal of Fluid
Mech. 2002,466,343-363.
[8] J. Prakash and A.Ogulu. “Unsteady two dimensional flow of a radiating and chemically reacting MHD fluid
wih time dependent suction”. Indian Journal of Pure and Applied Physics.2006,44,805-810.
[9] Ling S.C. Nazar R., Pop.I “Steady mixed convection boundary layer flow over a vertical flat surface in a
porous medium filled with water at 4 degree variable surface heat flux”.Transport in Porous Media.2007,3,307-
321.
[10]R.Muthucumarasamy. “Effects of heat and mass transfer on flow past an oscillatory vertical plate with variable temperature”. International Journal of Applied Math and Mech.2008,4,59-65.
[11]R.Muthucumarasamy and B.Janakiraman. “Mass transfer effects on isothermal vertical oscillating plate in the presence of chemical reaction”. International Journal of Applied math and Mech.2008,4,66-74
[12] M.C.Raju,S.V.K. Verma, P.V.Reddy and S.Saha.”Soret Effect due to Natural convection between heated
inclined plates with magnetic field”.International Journalof Mechanical Engineering,2008,39,65-70.
[13] Balamuguran K.S., Varma S.V.K. and Iyengar N.ch.S.N. “Chemcial reaction and thermo diffusion effects
on MHD three dimensional free convection coquette flow with Heat Absorpton”. International Journal of
Advances in Science and Technolgoy.2011.3,58-72.
[14] N.Senapati and R.K.Dhal . “Magnetic effect on mass and heat transfer of hydrodynamic flow past a vertical
oscillating plate in the presence of chemical reaction”.AMSE.2011,79,60-66.
[15] S.S. Das (et.al) “Discussed the combined natural convection and mass transfer effects on unsteady flow
past an infinite vertical porous plate embedded in a porous medium with heat source”.International Journal of
Energy and Environment.2012,3,591-604.

Dr.K.Balamurugan., Associate Professor, Department of Mathematics, Government Arts College, Tiruvannamalai, India. kaliyaperumalbalamurugan@yahoo.co.in

Key words: Heat Transf er, Mass Transf er, Porous Medium, Chemic al eff ects , permeability param eter, Gras hof Number, Prandtl number, Skin fric tion.

1. Introduction

2. Formulation of the Problem

Continuity Equation:

Momentum Equation:

Energy Equation:

Concentration Equation:

Boundary Conditions of the problem are:

Now, Introducing the following non- dimensional variables and parameters.

,𝑇 = 𝑻 −𝑻∞

The Corresponding boundary conditions are:

First Order:

The Corresponding boundary conditions are

Zeroth Order:

The Corresponding boundary conditions are

First Order:

The Corresponding boundary conditions become,

3.1 Skin friction: The wall shear stress i.e. the skin friction at the wall is given by

4.Results and discussions:-

Velocity field: The flow parameters affecting the velocity flow field are permeability parameter Kp., Grashof

5.Conclusion

Appendix:-

Reference:

Dr.K.Balamurugan., Associate Professor, Department of Mathematics, Government Arts College, Tiruvannamalai, India. kaliyaperumalbalamurugan@yahoo.co.in

Dr.S.Anuradha., Professor, Department of Mathematics, Hindustan College of Arts and Science, Coimbatore.

Mr.R.Karthikeyan., Assistant Professor, Department of Mathematics, Ganesh College of Engineering, Salem.E.Mail:- karthilib007@yahoo.com