International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 1
ISSN 2229-5518
Application of wavelet packet analysis for speech synthesis
Vaishali Jagrit, Subhra Debdas, Chinmay chandrakar
—————————— ——————————
avelets are functions that satisfy certain mathematical requirements and are used in representing data or other functions .The fundamental idea behind wavelets is to analyze[1,2] according to scale. Indeed, some researchers in the wavelet field feel that, by using wavelets, one is adopting a whole new mindset or perspective in processing data. Wave- lets are functions that satisfy certain mathematical require- ments and are used in representing data or other functions. This idea is not new. Approximation using superposition of functions has existed since the early 1800's, when Joseph Fourier discovered that he could superpose sines and cosines to represent other functions. However, in wavelet analysis, the scale that we use to look at data plays a special role. Wavelet algorithms process data at different scales or resolutions. If we look at a signal with a large \window," we would notice gross features. Similarly, if we look at a signal with a small
\window," we would notice small features. The result in wavelet analysis is to see both the forest and the trees, so to speak. This makes wavelets interesting and useful. For many decades, scientists have wanted more appropriate functions than the sines and cosines which comprise the bases of Fourier analysis, to approximate choppy signals . By their definition, these functions are non-local (and stretch out to in unity). They therefore do a very poor job in approximating sharp spikes. But with wavelet analysis, we can use approximating functions[3] that are contained neatly in finite domains. Wave- lets are well-suited for approximating data with sharp discon- tinuities. The wavelet analysis procedure is to adopt a wavelet prototype function[4,5], called an analyzing wavelet or mother wavelet. Temporal analysis is performed with a contracted, high-frequency version of the prototype wavelet, while fre- quency analysis is performed with a dilated, low-frequency version of the same wavelet Because the original signal or
————————————————
Co-Author name is currently pursuing masters degree program in electric power engineering in University, Country, PH-01123456789. E-mail: au-
(This information is optional; change it according to your need.)
function can be represented in terms of a wavelet expansion (using coefficients in a linear combination of the wavelet func- tions), data operations can be performed using just the corres- ponding[6] wavelet coefficients. And if you further choose the best wavelets adapted to your data, or truncate the coefficients below a threshold, your data is sparsely represented. This sparse coding[7,8] makes wavelets an excellent tool in the field of data compression. Other applied fields that are making use of wavelets include astronomy, acoustics, nuclear engineering, sub-band coding, signal and image processing, neurophysiol- ogy, music, magnetic resonance imaging, speech discrimina- tion, optics, fractals, turbulence, earthquake-prediction, radar, human vision, and pure mathematics applications such as solving partial differential equations.
Wavelets are functions that satisfy certain mathematical re- quirements and are used in representing data or other func- tions. The basic idea of the wavelet transform is to represent any arbitrary signal ‗X‘ as a superposition of a set of such wavelets or basis functions. These basis functions are ob- tained from a single photo type wavelet called the mother wavelet by dilation (scaling) and translation (shifts).
Low frequencies are examined with low temporal resolution
while high frequencies with more temporal resolution. A
wavelet transform combines both low pass and high pass fil-
tering in spectral decomposition of signals.
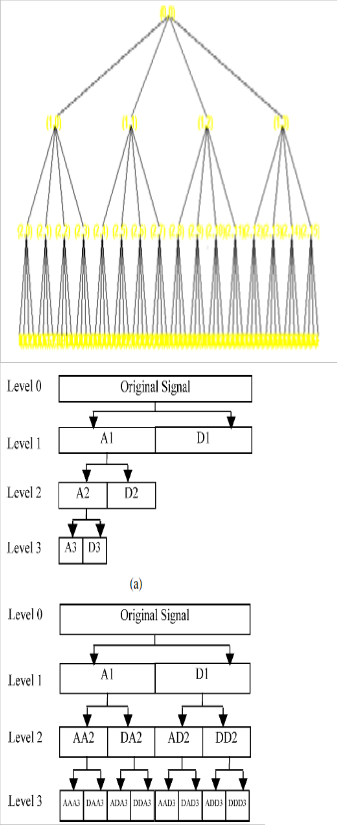
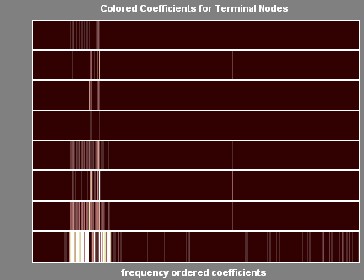
Ideas of wavelet packet is the same as wavelet, the only differ- ence is that wavelet packet offers a more complex and flexible analysis because in wavelet packet analysis the details as well as the approximation are splited. Wavelet packet decomposi- tion gives a lot of bases from which you can look for the best representation with respect to design objectives. The wavelet packet tree for 3-level decomposition is construct the
IJSER © 2012
International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 2

ISSN 2229-5518
Information content of decomposed component (approxi- mation and details) may be greater than the information con- tent of components, which has been decomposed. In this pa- per the sum of information of decomposed component (child node) is checked with information of component.
In wavelet analysis that every coefficient is associated with a function either a scaling function or a wavelet function de- pending on whether it is a ‗smooth‘ or ‗detail‘ coefficient. In the wavelet analysis the value are move from higher scale to lower scale and the basic function do not change. In this anal- ysis it can be split on detail coefficient lead to change in basis
set and these basis sets are called ‗wavelet packets‘.
The 8 data on the leaf nodes having 8 coefficients. These 8 coefficients are associated with 8 different functions. The func- tions associated with first two (on the left) are scaling and wavelet function with which started. All others are complex shaped function derived from wavelet function. This change in shape poses a problem in interpretation of the original sig- nal. Wavelet packet analysis leads to different basis function.
A sequence of function {W[k]}k=0k=+∞ from a given function
W[0] as follows:
W[0](t)=Ø(t), W[1](t)=ψ(t)
J=scale parameter and k= translation parameter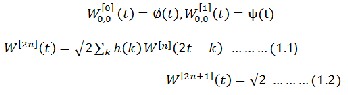
Wj,k[0](t) =Ø(2jt-k), Wj, [1](t)=ψ(2jt-k) This means
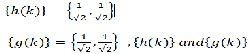
Let n=0, W[0] (t)= Haar scaling function Ø(t),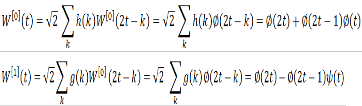
are Haar scaling and wavelet function filter coefficients.
best tree. Shannon entropy criteria find the information con-
tent of signal ‗S‘
Now let n=1 in eq. (1.1) and (1.2),![]()
IJSER © 2012
International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 3
ISSN 2229-5518
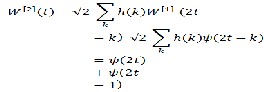
..…(1.3)![]()
![]()
The plot of the function W[2](t) and W[3](t). Now, let n=2 in eq.(1.1) and (1.2),
By equation (1.3),
…..(1.4)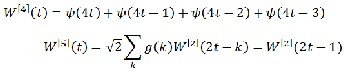
By equation (1.3),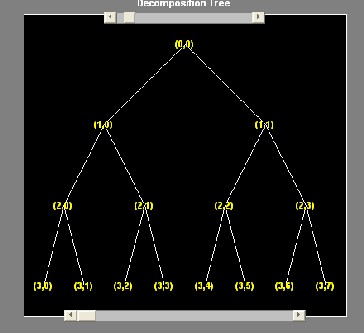
……(1.5)![]()
This process can be continued for n=∞.
..….(1.6)
For any orthogonal wavelet system some condition are apply:
(1)
are of same length and they are orthogonal.
(2) A particular W[n](t) and its integer translate W[n](t―k)
are orthogonal.
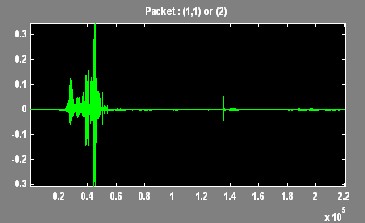
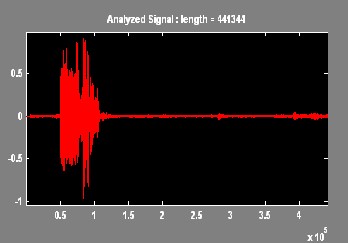
IJSER © 2012
International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 4
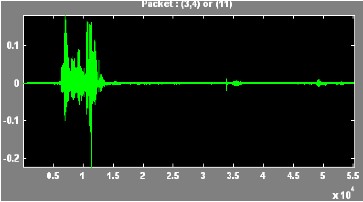
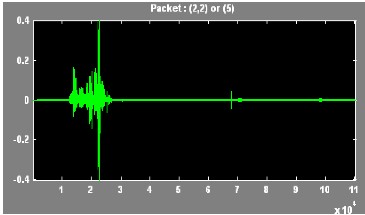
ISSN 2229-5518
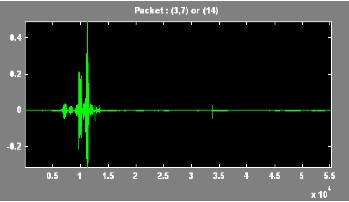
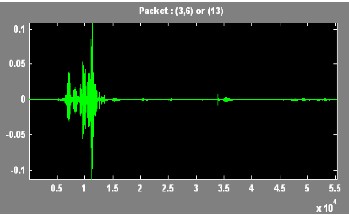
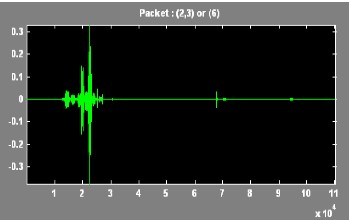
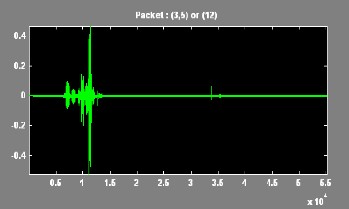
IJSER !b) 2012
International Journal of Scientific & Engineering Research, Volume 3, Issue 1, January-2012 5
ISSN 2229-5518
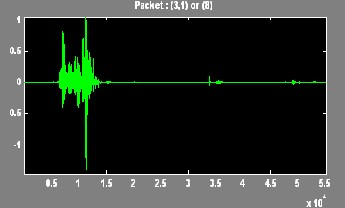
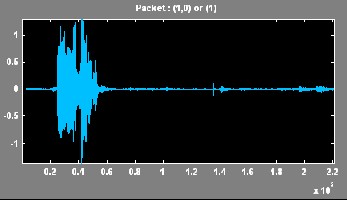
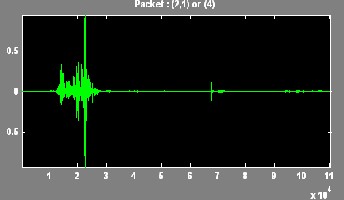
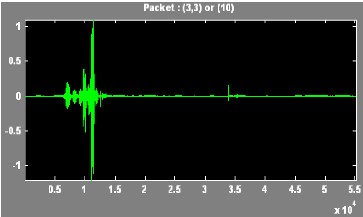
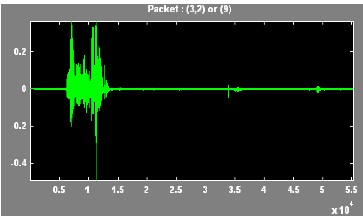
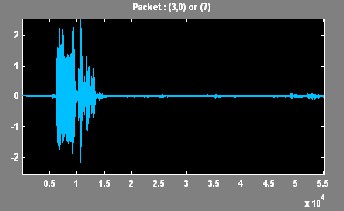
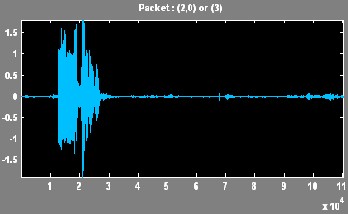
In this paper, the Wavelet Packet Best Tree using Shannon entropy has been presented. An extensive result has been tak- en on different voice signal. The results of discrete wavelet transform and the wavelet packet best tree are compared.
[1] M. Zimmermann and K. Dostert, ―Analysis and modeling of impulse noise in broadband power line communications,‖ IEEE Trans. Electro- magn. Compat., vol. 44, no. 1, pp. 249–258, Feb. 2002.
[2] J. Nguimbis, X. Jiang, and S. J. Cheng, ―Noise characteristics investiga- tion and utilization in low voltage powerline communication,‖ in Proc. IEEE Power Engineering Soc. Winter Meeting, vol. 3, Jan. 2000, pp. 2035–
2040.
[3] D. Cooper and T. Jeans, ―Narrowband, low data rate communications on the low voltages mains in the CENELES frequencies-Part I: Noise and attenuation,‖ IEEE Trans. Power Del., vol. 17, no. 3, pp. 718–723, Jul. 2002.
[4] C. J. Kim and M. F. Chouikha, ―Attenuation characteristic of high rate
home-networking PLC signal,‖ IEEE Trans. Power Del., vol. 17, no. 4, pp.
945–950, Oct. 2002.
[5] H. He, S. Cheng, Y. Zhang, and J. Nguimbis, ―Analysis of reflection of signal transmitted in low voltage power line with complex wavelet,‖
IEEE Trans. Power Del., vol. 19, no. 1, pp. 86–91, Jan. 2004
[6]Lokenath Debnath, ―Wavelet Transforms and Time- Frequency Signal
Analysis‖, Birkhauser, ISBN-0-8176-4104-1, 2001.
[7] Rudra Pratap, ― Getting Started with MATLAB‖ A quick introduction
for Scientists and Engineers, Oxford, ISBN-0-19-515014-7, 2003
[8] Howard L. Resnikoff, Raymond O. Wells, Jr., ―Wavelet Analysis‖ The
scalable Structure of Information, Springer, ISBN-0-387-98383-X, 1998
IJSER © 2012