A_Comparative_study_on_Breast_Cancer_Prediction_Using_RBF_and

International Journal of Scientific & Engineering Research, Volume 2, Issue 1, January-2011 1

ISSN 2229-5518

A Comparative study on Breast Cancer

Prediction Using RBF and MLP

J.Padmavathi

Lecturer, Dept. Of Computer Science, SRM University, Chennai

Abstract- In this article an attempt is made to study the applicability of a general purpose, supervised feed forward neural network with one hidden layer, namely. Radial Basis Function (RBF) neural network. It uses relatively smaller number of locally tuned units and is adaptive in nature. RBFs are suitable for pattern recognition and classification. Performance of the RBF neural network was also compared with the most commonly used Multilayer Perceptron network model and the classical logistic regression. W isconsin breast cancer data is used for the study.

Keywords - Artificial neural network, logistic regression, multilayer perceptron, radial basis function, supervised learning.

1.0 INTRODUCTION

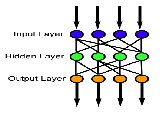
MULTILAYER Perceptron (MLP) network models are the popular network architectures used in most of the research applications in medicine, engineering, mathematical modeling, etc.1. In MLP, the weighted sum of the inputs and bias term are passed to activation level through a transfer function to produce the output, and the units are arranged in a layered feed-forward topology called Feed Forward Neural Network (FFNN). The schematic representation of FFNN with ‘n’ inputs, ‘m’ hidden units and one output unit along with the bias term of the input unit and hidden unitis given in Figure 1.

Figure 1. Feed forward neural network.

An artificial neural network (ANN) has three layers: input layer, hidden layer and output layer. The hidden layer vastly increases the learning power of the MLP. The transfer or activation function of the network modifies the input to give a desired output. The transfer function is chosen such that the algorithm requires a response function with a continuous, single-valued with first derivative existence. Choice of the number of the hidden layers, hidden nodes and type of activation function plays an important role in
model constructions[2-4]
Radial basis function (RBF) neural network is based on supervised learning. RBF networks were independently proposed by many researchers[5],[6],[7],[8],[9] and are a popular alternative to the MLP. RBF networks are also good at modeling nonlinear data and can be trained in one stage rather than using an iterative process as in MLP and also learn the given application quickly. They are useful in solving problems where the input data are corrupted with additive noise. The transformation functions used are based on a Gaussian distribution. If the error of the network is minimized appropriately, it will produce outputs that sum to unity, which will represent a probability for the outputs. The objective of this article is to study the applicability of RBF to diabetes data and compare the results with MLP and logistic regression.

2.0 RBF NETWORK MODEL

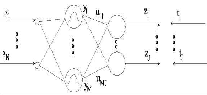
The RBF network has a feed forward structure consisting of a single hidden layer of J locally tuned units, which are fully interconnected to an output layer of L linear units. All hidden units simultaneously receive the n-dimensional real valued input vector X (Figure 2).

Figure 2. Radial basis function neural network.

The main difference from that of MLP is the absence of hidden-layer weights. The hidden-unit outputs are not calculated using the weighted-sum
mechanism/sigmoid activation; rather each

International Journal of Scientific & Engineering Research, Volume 2, Issue 1, January-2011 2

ISSN 2229-5518

hidden-unit output Zj is obtained by closeness of the input X to an n-dimensional parameter vector
µj associated with the jth hidden unit[10,11]. The response characteristics of the jth hidden unit ( j =
1, 2, @, J) is assumed as, 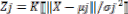eqn(1).
where K is a strictly positive radially symmetric function (kernel) with a unique maximum at its
‘centre’ mj and which drops off rapidly to zero
away from the centre. The parameter 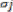is the width of the receptive field in the input space from unit j. This implies that Zj has an appreciable value
only when the distance is smaller than the
width 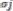. Given an input vector X, the output of the RBF network is the L-dimensional activity vector Y, whose lth component (l = 1, 2 @@L) is given by,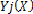 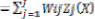eqn(2).
For l = 1, mapping of eqn. (1) is similar to a polynomial threshold gate. However, in the RBF network, a choice is made to use radially symmetric kernels as ‘hidden units’. RBF networks are best suited for approximating continuous or piecewise continuous real-valued mapping

f : Rn -7 RL, where n is sufficiently small. These

approximation problems include classification problems as a special case. From eqns (1) and (2), the RBF network can be viewed as approximating a desired function f (X) by superposition of non- orthogonal, bell-shaped basis functions. The degree of accuracy of these RBF networks can be controlled by three parameters: the number of basis functions used, their location and their width[10–13]. In the present work we have assumed a Gaussian basis function for the hidden units given as Zj for j = 1, 2, @@J, where

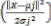eqn(3). and mj and sj are mean
and the standard deviation respectively, of the jth
unit receptive field and the norm is the Euclidean.

2.1 TRAINING OF RBF NEURAL NETWORKS

A training set is an m labelled pair {Xi, di} that represents associations of a given mapping or samples of a continuous multivariate function. The sum of squared error criterion function can be considered as an error function E to be minimized over the given training set. That is, to develop a training method that minimizes E by adaptively updating the free parameters of the RBF network.
These parameters are the receptive field centres mj
of the hidden layer Gaussian units, the receptive field widths , and the output layer weights (wij). Because of the differentiable nature of the RBF network transfer characteristics, one of the training methods considered here was a fully supervised gradient-descent method over E[7,9]. In particular,

µj,aj and wij are updated as follows:

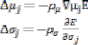
eqn(4). eqn(5).

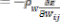
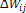eqn(6)

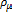
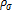
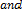
where , , are small positive constants. This method is capable of matching or exceeding
the performance of neural networks with back-
propagation algorithm, but gives training comparable with those of sigmoidal type of FFNN. The training of the RBF network is radically different from the classical training of standard FFNNs. In this
case, there is no changing of weights with the use of the gradient method aimed at function minimization. In RBF networks with the chosen type of radial basis function, training resolves itself into selecting the centres and dimensions of the functions and calculating the weights of the output neuron. The centre, distance scale and precise shape of the radial function are parameters of the model, all fixed if it is linear. Selection of the centres can be understood as defining the optimal number of basis functions and choosing the elements of the training set used in the solution. It was done according to the method of forward selection[15]. Heuristic operation on a given defined training set starts from an empty subset of the basis functions. Then the empty subset is filled with succeeding basis functions with their centres marked by the location of elements of the training set; which generally decreases the sum-squared error or the cost function. In this way, a model of the network constructed each time is being completed by the best element. Construction of the network is continued till the criterion demonstrating the quality of the model is fulfilled. The most commonly used method for estimating generalization error is the cross-validation
error.

2.2 FORMULATION OF NETWORK MODELS FOR WISCONSIN BREAST CANCER DATA

International Journal of Scientific & Engineering Research, Volume 2, Issue 1, January-2011 3

ISSN 2229-5518

The RBF neural network architecture considered for this application was a single hidden layer with Gaussian RBF. The basis function f is a real function of the distance (radius) r from the origin,
and the centre is c. The most common choice of f
includes thin-plate spline, Gaussian and multiquadric. Gaussian-type RBF was chosen here due to its similarity with the Euclidean distance and also since it gives better smoothing and interpolation properties[17].
The choice of nonlinear function is not usually a
major factor in network performance, unless there is an inherent special symmetry in the problem. Training of the RBF neural network involved two critical processes. First, the centres of each of the J Gaussian basis functions were fixed to represent the density function of the input space using a dynamic ‘k means clustering algorithm’. This was accomplished by first initializing the set of Gaussian centres µj to random values. Then, for any arbitrary input vector X(t) in the training set, the closest Gaussian centre, µj, is modified as:

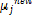
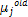= + a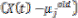 eqn(7).

where a is a learning rate that decreases over time. This phase of RBF network training places the weights of the radial basis function units in only those regions of the input space where significant data are present. The parameter aj is set for each Gaussian unit to equal the average distance to the two closest neighboring Gaussian basis units. If
µ1and µ 2 represent the two closest weight centres to Gaussian unit j, the intention was to size this parameter so that there were no gaps between basis functions and only minimal overlap between adjacent basis functions were allowed. After the Gaussian basis centres were fixed, the second step of the RBF network training process was to determine the weight vector W which would best
approximate the limited sample data X, thus
leading to a linear optimization problem that could be solved by ordinary least squares method. This avoids the problem of gradient descent methods and local minima characteristic of back propagation algorithm[18].
For MLP network architecture, a single hidden
layer with sigmoid activation function, which is optimal for the dichotomous outcome, is chosen. A back propagation algorithm based on conjugate
gradient optimization technique was used to
model MLP for the above data. A logistic regression model[22] was fitted using the same input vectors as in the neural networks and cancer status as the binary dependent variable. The efficiency of the constructed models was evaluated by comparing the sensitivity, specificity and overall correct predictions for both
datasets. Logistic regression was performed using logistic regression in SPSS package [22] and MLP and RBF were constructed using MATLAB.

3.0 RESULTS

Wisconsin data set with 580 records were used for the research. The MLP architecture had five input variables, one hidden layer with four hidden nodes and one output node. Total number of weights present in the model was 29. The best MLP was obtained at lowest root mean square of 0.2126. Sensitivity of the MLP model was 92.1%, specificity was 91.1% and percentage correct prediction was
91.3%. RBF neural networks performed best at ten
centres and maximum number of centres tried was
18. Root mean square error using the best centres was 0.3213. Sensitivity of the RBF neural network model was 97.3%, specificity was 96.8% and the percentage correct prediction was 97%. Execution time of RBF network is lesser than MLP and when compared.

Table 1. Comparative predictions of three models

Database Model	Sensitivity (%)	Specificity (%)	Correct prediction (%)
LOGISTIC REGRESSION	75.5	72.6	73.7
MLP	92.1	91.1	91.3
RBFNN	97.3	96.8	97.0

With logistic regression, neural networks take slightly higher time. Logistic regression performed on the external data gave sensitivity of 75.5%, specificity of 72.6% and the overall correct prediction of 73.7%. MLP model was 94.5%, specificity was 94.0% and percentage correct prediction was 94.3%. The RBF neural network performed best at eight centres and maximum number of centres tried was 13. Root mean square
The comparative results of all the models are

International Journal of Scientific & Engineering Research, Volume 2, Issue 1, January-2011 4

ISSN 2229-5518

presented in Table 1. The results indicate that the RBF network has a better performance than other models.

4.0 CONCLUSION

The sensitivity and specificity of both neural network models had a better predictive power compared to logistic regression. Even when compared on an external dataset, the neural network models performed better than the logistic regression. When comparing, RBF and MLP network models, we find that the former output forms the latter model both in test set and an external set. This study indicates the good predictive capabilities of RBF neural network. Also the time taken by RBF is less than that of MLP in our application. The limitation of the RBF neural network is that it is more sensitive to dimensionality and has greater difficulties if the number of units is large.
Here an independent evaluation is done using
external validation data and both the neural network models performed well, with the RBF model having better prediction. The predicting capabilities of RBF neural network had showed good results and more applications would bring out the efficiency of this model over other models. ANN may be particularly useful when the primary goal is classification and is important when interactions or complex nonlinearities exist in the dataset [23]. Logistic regression remains the clear choice when the primary goal of model development is to look for possible causal relationships between independent and dependent variables, and one wishes to easily understand the effect of predictor variables on the outcome.
There have been ingenious modifications and restrictions to the neural network model to broaden its range of applications. The bottleneck networks for nonlinear principle components and networks with duplicated weights to mimic autoregressive models are recent examples. When classification is the goal, the neural network model will often deliver close to the best fit. The case of missing data is to be continued.

References

1. Michie,D.Spiegelhalter,D.J., and Taylor. Machine learning, neural and statistical classification.

2. Cherkassky, V., Friedman, J.H., and Wechsler, H., eds. (1994), From Statistics to Neural Networks: Theory and Pattern Recognition Applications, Berlin: Springer-Verlag

3. Breast Cancer.org http://www.nationalbreastcancer.org

4. Vaibhav narayan Chunekar, Shivaji Manikarao Jadhav, Application of Backpropagation to detect Breast cancer BIST-2008, July,2008,180-181.

5. Kocur CM, Rogers SK, Myers LR, Burns T,Kabrisky M, Steppe J Using neural networks to select wavelet features for breast cancer diagnosis,IEEE Engineering in Medicine and Biology Magazine 1996:may/june;95-105.

6. Rumelhart, D. E., Hinton, G. E. and Williams, R. J., Learning representation by back-propagating errors. Nature, 1986, 323, 533–536.

7. Hecht-Nielsen, R., Neurocomputing, Addison-

Wesley, Reading, MA, 1990.

8. White, H., Artificial Neural Networks. Approximation and Learning Theory, Blackwell, Cambridge, MA,

1992.

9. White, H. and Gallant, A. R., On learning the derivatives of an unknown mapping with multilayer feedforward networks. Neural Networks., 1992, 5, 129–138.

10. Broomhead, D. S. and Lowe, D., Multivariate functional interpolation and adaptive networks. Complex Syst., 1988, 2, 321–355.

11. Niranjan, M. A., Robinson, A. J. and Fallside, F.,

Pattern recognition with potential functions in the context of neural networks.

12. Park, J. and Sandberg, I. W., Approximation and radial basis function networks. Neural Comput.,

1993, 5, 305–316.

13. Wettschereck, D. and Dietterich, T., Improving the performance of radial basis function networks by learning center locations.

14. In Advances in Neural Information Processing

Systems, Morgan Kaufman Publishers, 1992, vol. 4, pp. 1133–1140.

15. Orr, M. J., Regularisation in the selection of radial basis function centers. Neural Comput., 1995, 7,

606–623.

16. Bishop, C. M., Neural Networks for Pattern

Recognition, OxfordUniversity Press, New York,

1995.

17. Curry, B. and Morgan, P., Neural networks: a need for caution.Omega – Int. J. Manage. Sci., 1997, 25,

123–133.

18. Hornik, K., Multilayer feedforward networks are universal approximatorsNeural Networks, 1989, 2,

359–366.

19. Tu, J. V., Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes.

J. Clin. Epidemiol., 1996, 49, 1225–1231.

International Journal of Scientific & Engineering Research, Volume 2, Issue 1, January-2011 5

ISSN 2229-5518

20. Shepherd, A. J., Second-order methods for neural networks: Fast and reliable training methods for multi-layer perceptions. Perspectivesin Neural Computing Series, Springer, 1997.

21. Hosmer, D. W. and Lemeshow, S., Applied Logistic

Regression,John Weiley, New York, 1989.

MATLAB 5.0.

23. “Non-linear system identification based on RBFNN using improved particle swarm Optimization, Ji Zhao, Wei Chen Wenbo Xu, IEEE Computer Dociety,2009 pg-409-413.