International Journal of Scientific & Engineering Research Volume 2, Issue 12, December-2011 1

ISSN 2229-5518

A simple approach to fuzzy critical path analysis in project networks

Shakeela Sathish, K. Ganesan
Abstract— In this paper, we propose a new approach to critical path analysis in a project network whose activity times are uncertain. The uncertain parameters in the project network are represented by fuzzy numbers. We use fuzzy arithmetic and a fuzzy ranking method to determine the fuzzy critical path of the project network without converting the fuzzy activity times to classical numbers. The proposed method is compared with the existing method using examples.
Index Terms—Trapezoidal fuzzy numbers, Fuzzy arithmetic, Ranking, Project network, Critical path, Floats, Eearliest start, Eearliest finish, Latest start, Latest finish.

1 INTRODUCTION

—————————— • ——————————
a number of possible sources like: activities may take more or
CTIVITY networks are highly useful for the perform- ance evaluation of many types of projects. A con- structed network is an important tool in the planning
and control of actual project implementation. Project man- agement is divided in to different subjects like scheduling, control, time management, resource management and cost management among which time management is more signifi- cant.
Critical path method is a network-based method designed for planning and managing of complicated projects in real world applications. The main purpose of critical path method is to evaluating project performance and to identifying the critical activities on the critical path so that the available resources could be utilized on these activities in the project network in order to reduce project completion time. With the help of the critical path, the decision maker can adopt a better strategy of optimizing the time and the available resources to ensure the earlier completion and the quality of the project.
The successful implementation of critical path method re- quires the availability of clear determined time duration for each activity. However in real life situations, project activities are subject to considerable uncertainty that may lead to nu- merous schedule disruptions. This uncertainity may arise from
• Shakeela Sathish
Department of Mathematics,
Faculty of Engineering and Technology,
SRM University,
Ramapuram Campus, Chennai - 600 091, India
Email: shakeela_sathish@yahoo.co.in
• K. Ganesan
Department of Mathematics,
Faculty of Engineering and Technology,
SRM University,
Kattankulathur, Chennai - 603203, India
Email: gansan_k@yahoo.com
less time than originally estimated, resources may become unavailable, material may arrive behind schedule, due dates may have to be changed, new activities may have to be incor- porated or activities may have to be dropped due to changes in the project scope, weather conditions may cause severe de- lays, etc. A disrupted schedule incurs higher costs due to missed duedates and deadlines, resource idleness, higher work-in-process inventory and increased system nervousness due to frequent rescheduling. As a result, the conventional approaches, both deterministic and random process, tend to be less effective in conveying the imprecision or vagueness na- ture of the linguistic assessment. Consequently, the fuzzy set theory can play a significant role in this kind of decision mak- ing environment to tackle the unknown or the vagueness about the time duration of activities in a project network. To effectively deal with the ambiguities involved in the process of linguistic estimate times, the trapezoidal fuzzy numbers are used to characterize fuzzy measures of linguistic values.
Dubois et al [5] extended the fuzzy arithmetic operations to compute the latest starting time of each activity in a project network. Hapke et al. [7] used fuzzy arithmetic operations to compute the latest starting time of each activity in a project network. To find critical path in a fuzzy project network Yao et al. [11] used signed distance ranking of fuzzy numbers. Chen et al. [2] used defuzzification method to find possible critical paths in a fuzzy network.
Dubois et al [6] assigns a different level of importance to each activity on a critical path for a randomly chosen set of activi- ties. To deal with completion time management and the criti- cal degrees of all activities for a project network. C. T. Chen and S. F. Huang, applied fuzzy method for measuring critical- ity in project network. Ravi Shankar et al [10] proposed an analytical method for finding critical path in a fuzzy project network.

IJSER © 2011 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 2, Issue 12, December-2011 2

ISSN 2229-5518

(i). if
a1 = a3 , then a-
is known as a triangular fuzzy
In this paper, we propose a new method to find the critical
path in a project network with out defuzzifying the fuzzy ac- tivity durations. The proposed method is based upon a new
number.

(ii). if a1 = a2 , a3 = a4 , then a-

or an interval number.
is an interval fuzzy number
fuzzy arithmetic given in [3]. It makes project analysis in fuzzy
(iii). If

a2 - a1 = a4 - a3 , then a-

is known as a symmetric
environment more accurate. Finally illustrative numerical ex-
amples are given to demonstrate validity of the proposed me- thod. The rest of this paper is organized as follows: In section
2, we recall the basic concept of fuzzy numbers, ranking and
trapezoidal fuzzy number.
2.2 [3] Arithmetic operations on trapezoidal fuzzy numbers
other related results. In section 3, we introduce fuzzy critical
Let
a- = (a1 , a2 , a3 , a4 ) and
b- = (b , b , b , b ) be any two trape-
path analysis. In section 4 numerical examples are given to illustrate the theory.

2 PRELIMANARIES

The aim of this section is to present some notations, notions and results which are useful in our further consideration.
zoidal fuzzy numbers in F(R) . The arithmetic operations on
- and b- are defined as:
a- * b- = {a * b /a ∈ a- , b ∈ b- } , where ∗∈{+, −, i, ÷}
i i i i
In particular, for any two trapezoidal fuzzy numbers
a- = (a , a , a , a ) and b- = (b , b , b , b ) , we define
Definition 2.1
A fuzzy set a-
defined on the set of real numbers R is said to

1 2 3 4

Addition :

1 2 3 4

a- + b- = (a , a , a , a ) + (b , b , b , b )
be a fuzzy number if its membership function has the follow- ing characteristics:
= (a1 + b1 , a2 + b2 , a3 + b3 , a4 + b4 )
(i). a-
is convex, i.e.
Subtraction :
a- - b- = (a , a , a , a ) - (b , b , b , b )
a( λx1 + (1 - λ )x2 ) = minimum{ a(x1 ), a(x2 )}, for all x1 , x2 ∈R and λ ∈[0,1]
= (a1 - b1 , a2 - b2 , a3 - b3 , a4 - b4 )
2.3 Ranking of trapezoidal fuzzy numbers
An efficient approach for comparing the fuzzy numbers is by
(ii). a-
is normal i.e., there exists an
x 0 ∈ R
such that
the use of a ranking function
ℜ : F(R) → R , where F( R ) is a

a- (x 0 ) = 1

set of fuzzy numbers defined on set of real numbers, which
(iii).
a- is Piecewise continuous.
maps each fuzzy number into a real number, where a natural
order exists i.e.,
Definition 2.2
A fuzzy number a-
in R is said to be a trapezoidal fuzzy
For every a- = (a1 , a2 , a3 , a4 ) ∈ F(R) , the ranking function
number if its membership function lowing characteristics:

a- : R → [0,1]

has the fol-
ℜ : F(R) → R
defined as

 (x - a 1 ) , a

 (a 2 - a 1 )

1 ≤ x ≤ a 2

ℜ(a- ) =
 a1 + 2a2 + 2a3 + a4 

 

 1 , a 2 ≤ x ≤ a 3

 6 

a- = 

(x - a )

For any two trapezoidal fuzzy numbers

a- = (a1 ,a2 ,a3 ,a4 )

and

 4 , a

≤ x ≤ a

b- = (b ,b ,b ,b ) , we have the following comparison

 (a - a ) 3 4

1 2 3 4

 3 4

 0 , o t h e r w i s e

We denote this trapezoidal fuzzy number by
a- = (a1 , a2 , a3 , a4 )
a- > b-
a- ≺ b-
iff ℜ(a- ) > ℜ(b- )
iff ℜ(a- ) < ℜ(b- )
We use F(R) to denote the set of all trapezoidal fuzzy numbers.
a- ≈ b-
iff ℜ(a- ) = ℜ(b- )
For an interval a- = [a1 , a2 ] , define
a- : R → [0,1] as

A trapezoidal fuzzy number a- = (a1 , a2 , a3 , a4 ) is said to be posi- tive if ℜ(a- ) > 0

1, for all x ∈[a1 , a2 ]
a- (x) = 
0, otherwise
That is a- > 0-
if ℜ(a- ) > 0 . Also

a- ≈ 0- if

ℜ(a- ) = 0 and
Then a-

is a fuzzy number. That is an interval can be viewed
a- ≺ 0- if ℜ(a- ) < 0. If a- ≈ b- , then the trapezoidal fuzzy numbers

a- and b- are said to be equivalent.

as a fuzzy number whose membership function takes value 1
over the interval and 0 anywhere else. Hence every closed and bounded interval is a special type of fuzzy number.
In a trapezoidal fuzzy number,
3 FUZZY CRITICAL PATH ANALYSIS
A fuzzy project network is an acyclic digraph, where the ver- tices represent events, and the directed edges represent the

IJSER © 2010 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 2, Issue 12, December-2011 3

ISSN 2229-5518

activities, to be performed in a project. We denote this fuzzy

project network by N- = (V-, A- , T- ).

membership functions are piecewise continuous, hence the quantities such as earliest fuzzy event time E-S , the latest
Let V- = {v-1 ,v-2 ,v-3 , ...,v-n } be the set of fuzzy vertices (events),
fuzzy event time

L-S i and the floats T-

are also trapezoidal
where v-1
and v-n
are the tail and head events of the project,
fuzzy numbers for an event i respectively.
and each

v-i

belongs to some path from

v-1

tov-n . Let

A- ∈(V- ×× V× -)

be the set of directed edges
Step 1: Identify Fuzzy activities in a fuzzy project
A- = {a- ij = ( v- i , v- j )/ for v- i , v- j ∈ V- } , that represents the activities
to be performed in the project. Activity a- ij is then represented
Step 2: Establish precedence relationships of all fuzzy activities by applying a fuzzy ranking function.
by one, and only one, arrow with a tail event v-i
eventv- j . For each activity a- ij , a fuzzy number
and a head

tij ∈ T- is de-

Step 3: Construct the fuzzy project network with trapezoidal
fined as the fuzzy time required for the completion of a- ij . A
fuzzy numbers as fuzzy activity times
critical path is a longest path from the initial event v-1
to the
terminal event tov-n
of the project network, and an activity a- ij
on a critical path is called a critical activity.
Step 4: Let E-S1 be the earliest fuzzy event time and L-S1 be the
3.1 Notations
latest fuzzy event time for the initial event v-1
of the project
network and assume that

E-S1 = L-S1 = 0- . Compute the earliest

-tij : The fuzzy activity time of activity a-

E-S j : The earliest fuzzy time of event v- j

fuzzy event time E-S j
of the event v- j
by using the formula

L-S i : The latest fuzzy time of event v-i

E- S j = max {E- Si + t-ij } (1)

i∈N: i → j

- - Step 5: Let

E-S n

be the earliest fuzzy event time and L-S n be

Tij : The total float of fuzzy activity aij

Pi: The i-th path of the fuzzy project network.
P: The set of all paths in a fuzzy project network.
the latest fuzzy event time for the terminal event v-n of the fuzzy project network and assume that E-S n = L-S n . Compute the
CPM (Pk): The fuzzy completion time of path Pk in a fuzzy
latest fuzzy event time L-S i
by using the following equation
project network.

-

- - -

- - are two fuzzy activi-

L-S = min{L-S - t- }

i∈N

(2)
Property 1 If aij = (v i ,v j ), amn = (v m ,v n )
-

a- iff there is a

ties, activity

aij

is a predecessor of activity mn
Step 6: Compute the total float T- of each fuzzy activity a- by
chain from event j to event m in project network.

ij ij

using the following equation
Property 2 If
-

a- ij = (v- i , v- j ), a- mn = (v- m , v- n )

are two fuzzy activi-

a- iff

- - - -
ties, activity aij
is an immediate predecessor of activity mn

Tij = {LS j - ES i - t ij }

(3)
either j = m, or there exists a chain from event j to event m in
the project network consisting of dummy activities only.
Hence we can obtain the earliest fuzzy event time, latest fuzzy event time, and the total float of every fuzzy activity by using
Property 3

CPM (P )=

∑ T- , P ∈ P

equations (1), (2) and (3).

k ij K

1 ≤ i < j ≤ n i, j ∈Pk

Definition 3.1 Assume that there exists a path PC in a fuzzy project network such that CPM (PC) = min {CPM (Pi) | Pi ∈ P},
then the path PC is a fuzzy critical path.
Theorem 1 Assume that the fuzzy activity times of all activities in a project network are trapezoidal fuzzy numbers, then there exists fuzzy critical path in the project network
3.1 Algorithm for Fuzzy critical activity
Let E-S and L-S be the earliest fuzzy event time, and the latest
Step 7: If T- = 0- , then the activity a- is said to be a Fuzzy crit- ical activity. That is activities with zero total float are called

Fuzzy critical activities, and are always found on one or more

Fuzzy critical paths.

Step 8: The length of the longest Fuzzy critical path from the start of the fuzzy project to its finish is the minimum time re- quired to complete the Fuzzy Project. This (or these) Fuzzy critical path(s) determine the minimum fuzzy project duration.
4 NUMERICAL EXAMPLES

i i In this section fuzzy project network problems are presented

fuzzy event time for event i, respectively. Functions that define
the earliest starting times, latest starting times and floats in terms of fuzzy activity durations are convex, normal whose
to demonstrate the computational process of fuzzy critical path analysis proposed above.

IJSER © 2011 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 2, Issue 12, December-2011 4

ISSN 2229-5518

Example-1:
Suppose that there is a project network with the set of fuzzy
Table 2: Calculation of total float for each activity in a fuzzy project network and critical path
events
V- = {1, 2, 3, 4, 5}, the fuzzy activity time for each activity
is shown in Table 1. All the durations are in hours.
Table 1: Activity duration of each activity in a fuzzy project network

3
1 4
5
2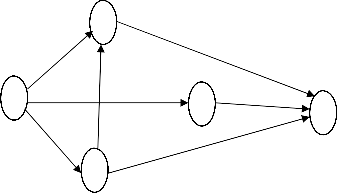

Figure 1: Fuzzy project network-I
Fuzzy critical path is 1 → 2 → 3 → 5
The minimum fuzzy project duration is the length of the fuzzy
critical path.
The fuzzy project duration is (100, 155, 205, 250) fuzzy hours.

IJSER © 2010 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 2, Issue 12, December-2011 5

ISSN 2229-5518

Example-2:
Suppose that there is a project network, as Figure 2, with the set of events V- = {1, 2, 3, 4, 5, 6}, the fuzzy activity time for each
activity as shown in Table 3. All the durations are in hours.
Table 4: Calculation of total float for each activity in a fuzzy project network and critical path
3
1 2 4 6
5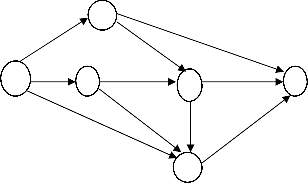

Figure 2: Fuzzy project network-II
Table 3: Fuzzy activity duration of each activity in Example 2.

Fuzzy critical path is 1 → 3 → 6
The minimum fuzzy project duration is the length of the fuzzy
critical path.
The fuzzy project duration is (9, 11, 14, 21) fuzzy hours.

IJSER © 2011 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 2, Issue 12, December-2011 6

ISSN 2229-5518

4 CONCLUSION
This paper proposes an algorithm to tackle the problem in fuzzy project analysis. The validity of the proposed me- thod is examined with numerical example.
REFERENCES
[1] S. Chanas, P. Zielinski, Critical path analysis in the network with fuzzy task times, Fuzzy sets and sys- tems, 122 (2001) 195-204.
[2] S.M. Chen and T.H. Chang, Finding Multiple Possible Critical Paths using Fuzzy PERT, IEEE Transactions on systems, man and cybernetics - PartA: systems and humans, Vol. 31, No.6., 2001.
[3] S.M. Chen, Fuzzy system reliability analysis using fuzzy number arithmetic operations, Fuzzy sets and systems, 64 (1994) 31-38.
[4] C.T. Chen and S.F. Huang, Applying fuzzy method for measuring criticality in project network, Information sciences, 177 (2007) 2448-2458.
[5] D. Dubois and H. Prade, Possibility Theory: An Ap- proach to Computerized Processing of Uncertainty, New York: Plenum, 1988.
[6] D.Dubois, H. Fargier, V.Galvagonon, On latest starting times and floats in task networks with ill-known dura- tions, European Journal of Operational Research 147 (2003) 266-280.
[7] M. Hapke and R. Slowinski, Fuzzy priority heuristics for project scheduling, Fuzzy sets and systems, 83(3) (1996) 291-299.
[8] G.J. Klir, B.Yuan, Fuzzy Sets and Fuzzy Logic: Theory and Applications, Prentice- Hall, International Inc.,
1995.
[9] D.L. Mon, C.H. Cheng, and H.C.Lu, “Application of fuzzy distribution on project management,” Fuzzy sets and systems, vol.73, no.3, pp.227-234, 1995.
[10] N. Ravi Shankar,V. Sireesha, P. Phani Booshan Rao, An analytical method for finding critical path in a fuzzy project network, Int.J.Contemp.Math.Sciences, 5(20) (2010) 953-962.
[11] S. Yao and F.T. Lin, Fuzzy Critical Path Method Based on Signed Distance ranking of fuzzy numbers, IEEE Transactions on systems, man and cybernetics-Part A: systems and humans, 30 (1) 2000.
[12] Zadeh, Fuzzy sets, Information and Control, 8 (1965)
338-353.

IJSER © 2010 http://www.ijser.org