International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 73

ISSN 2229-5518

A Survey paper on Secure AODV protocol in MANAET using RSA algorithm and Diffie-hellman algorithm

Prasad P. Lokulwar1 , Prof. Yogadhar Pandey2

Abstract:Mobile ad-hoc networks (MANTEs) are temporary networks that are built up momentarily in order to satisfy a certain emergency, for example, suppose that in an area of zero connectivity if there is a bomb blast then the local police would set up an ad-hoc network for communicating this emergency to the higher officials. Hence, this could save many lives. Ad-hoc networks are in a great demand now a days and have a lot of advantages like emergency control, short term connections for roaming subscribers, etc.But with this advantages there are disadvantages also, one such disadvantage is the security of MANETs which is very low as compared to the other permanent networks which is due to absence of central network database and due to absence of full network temporarily would also increase the cost of the system.W e have designed the Ad Hoc On Demand Routing Protocol (AODV) using RSA algorithm and diffie-hellman algorithm on platform NS. W hich is efficient as well as we have implemented the security technique so the we can prevent the data loss at the time of transmission and prevent from malicious node. W e also provide the security to public key and private key in network with the help of the diffie-hellman algorithm. This technique is help at the time of sending the private key to the destination node. After that the destination node create the secret key with the help of sender key and sender and destination node use the same key (secret key).

Keyword:, Aodv protocol, Diffie-hellman algorithm, MANET , NS2, private key, , public key, RSA ,secret key

1 INTRODUCTION:

WIRELESS ad hoc networks[6] are comprised of Mobile Nodes (MNs) that are self-organizing and cooperating to ensure routing of packets among themselves. They provide robust communication in a variety of hostile environments, such as communication for the military or in disaster recovery situations when all infrastructures are down.

• Prasad Lokulwar is currently pursuing masters degree program in computer science & engineering in RGT university, India, E-mail: prasadengg16@gmail.com
• Prof. Yogadhar Pandey is currently working as asst prof. in SIRT,Bhopal in RGTUniversity, India,
. E-mail: p_yogadhar@yahoo.co.in
Since the network topology of ad hoc networks is unstable and changes frequently with nodes mobility, traditional routing protocols in static networks are not efficient for ad hoc networks. Routing protocols for ad hoc networks can be
classified broadly as either proactive, reactive, or hybrid (combining both behaviors).
Proactive protocols continuously exchange network topology information so as to constantly monitor topology changes and use that knowledge for efficient, low latency data transmission. In their turn, proactive protocols can be classified into two categories: link state routing and distance vector routing. Common proactive routing protocols include Dynamic Destination-Sequenced Distance- Vector Routing (DSDV)[2], Optimized Link State Routing (OLSR), Multicast Optimized Link State Routing (MOLSR), etc.
Reactive protocols were introduced to remedy the above shortcomings. These adopt a lazy approach to communication requirements, where nodes reacts only on-demand to data transmission requests and perform path finding operations only when needed. Reactive protocols do effectively save channel and battery power usage as they generate fewer control packets when there is no demand for transmission. The most common reactive protocols include Ad Hoc On-Demand Distance Vector Routing (AODV)[3], Dynamic Source Routing (DSR), Source Routing-Based Multicast Protocol (SRMP), etc.

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 74

ISSN 2229-5518

2 ANALYSIS

2.1 AD HOC ON-DEMAND DISTANCE

VECTOR ROUTING PROTOCOL (AODV)

2.1.1 GENERAL WORKING OF AODV

Ad hoc On-Demand Distance Vector (AODV)
[3][9] routing is a routing protocol for mobile ad
hoc networks and other wireless ad-hoc networks.
It is jointly developed in Nokia Research Centre of
University of California, Santa Barbara and
University of Cincinnati by C. Perkins and S. Das.
It is an on-demand and distance-vector routing
protocol, meaning that a route is established by
AODV from a destination only on demand.AODV
is capable of both unicast and multicast routing. It
keeps these routes as long as they are desirable by
the sources. Additionally, AODV creates trees
which connect multicast group members. The trees
are composed of the group members and the nodes
needed to connect the members. The sequence
numbers are used by AODV to ensure the
freshness of routes. It is loop-free, self-starting, and
scales to large numbers of mobile nodes .AODV
define three types of control messages for route

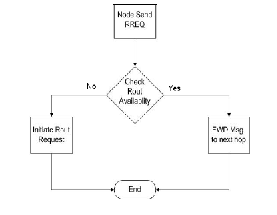
maintenance:

“Fig.(2.1)”: Basic AODV Protocol

2.2 Security AODV protocol USING RSA

Algorithm:

INTRODUCTION

Encryption is the act of encoding text so that others
not privy to the decryption mechanism (the "key")
cannot understand the content of the text.
Encryption has long been the domain of spies and
diplomats, but recently it has moved into the
public eye with the concern of the protection of
electronic transmissions and digitally stored data.
Standard encryption methods usually have two
basic flaws: A secure channel must be established
at some point so that the sender may exchange the
decoding key with the receiver; and There is no guarantee who sent a given message. Public key encryption has rapidly grown in popularity (and controversy, see, for example, discussions of the Clipper chip on the archives given below) because it offers a very secure encryption method that addresses these concerns. In a classic cryptosystem in order to make sure that nobody, except the intended recipient, deciphers the message, the people involved had to strive to keep the key secret. In a public-key cryptosystem. The public key cryptography solves one of the most vexing problems of all prior cryptography: the necessity of establishing a secure channel for the exchange of the key.
In cryptography, RSA (which stands for Rivest , Shamir and Adleman who first publicly described it) is an algorithm for public-key cryptography . It is the first algorithm known to be suitable for signing as well as encryption, and was one of the first great advances in public key cryptography. RSA is widely used in electronic commerce protocols, and is believed to be secure given sufficiently long keys and the use of up-to-date implementations.

OPERATION

The RSA algorithm involves three steps: key
generation, encryption and decryption.

Key generation

RSA involves a public key and a private key. The
public key can be known to everyone and is used
for encrypting messages. Messages encrypted with
the public key can only be decrypted using the
private key. The keys for the RSA algorithm are
generated the following way:
1. Choose two distinct prime numbers p and

o For security purposes, the

integers p and q should be chosen uniformly at
random and should be of similar bit-length. Prime
integers can be efficiently found using a primality
test.
2. Compute n = pq.

o n is used as the modulus for both

the public and private keys
3. Compute φ(pq) = (p − 1)(q − 1). (φ is Euler's
totient function).
4. Choose an integer e such that 1 < e < φ(pq),
and e and φ(pq) share no divisors other than 1 (i.e. e
and φ(pq) are coprime).

o e is released as the public key

exponent.

o e having a short bit-length and

small Hamming weight results in more efficient
encryption. However, small values of e (such as

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 75

ISSN 2229-5518

e = 3) have been shown to be less secure in some settings.

5. Determine d (using modular arithmetic)
gruence relation
.
o Stated differently, ed − 1 can be
evenly divided by the quotient (p − 1)(q − 1).

o This is often computed using the

extended Euclidean algorithm.

o d is kept as the private key

exponent.

The public key consists of the modulus n and the
public (or encryption) exponent e. The private key
consists of the private (or decryption) exponent d

which must be kept secret.

Encryption

Destination node transmits its public key (n,e) to
Source node and keeps the private key secret. then
source wants to send message M to Destination
It first turns M into an integer 0 < m < n by using an
agreed-upon reversible protocol known as a
padding scheme. It then computes the cipher text c
corresponding to:
This can be done quickly using the method of exponentiation by squaring. Source then transmits c to Destination.

Decryption

Destination can recover m from c by using her
private key exponent d by the following
Given m, Destination can recover the original message M by reversing the padding scheme. Example Of RSA Algorithm
Example of RSA with small numbers:

p = 47, q = 71, compute n = pq = 3337

Compute phi = 46 * 70 = 3220
Let e be 79, compute d = 79-1 mod 3220 = 1019
Public key is n and e, private key d, discard p and q.
Encrypt message m = 688, 68879 mod 3337 = 1570 =

Decrypt message c = 1570, 15701019 mod 3337 = 688

= m.

Thus RSA is very useful algorithm in order to obtain the security aware AODV protocol as it uses both the public key as well as the private key.

Diffie-hellman key exchange algorithm: Diffie- hellman key exchange is a public key algorithm .The purpose of the algorithm is to

enable two users to exchange a key securely thatcan then be used for subsequent encryption of message. The algorithm is limited to the exchange of keys. The diffie hellman algorithm depends for its effectiveness on the difficulty of computing discrete logarithms.
The steps for Diffie Hellman key exchange algorithm are:
Step 1 : GLOBAL PUBLIC ELEMENTS Select any prime no : 'q'
Calculate the primitive root of q : 'a' such that a<q
Step 2 : ASYMMETRIC KEY GENERATION BY USER 'A'
Select a random number as the private key XA
where XA < q
Calculate the public key YA where YA = aXA mod q
Step 3 : KEY GENERATION BY USER 'B' Select a random number as the private key XB where XB < q
Calculate the public key YB where YB = aXB mod q
Step 4 : Exchange the values of public key between
A & B
Step 5 : SYMMETRIC KEY (K) GENERATION BY USER 'A'
K= YB XA mod q
Step 6 : SYMMETRIC KEY (K) GENERATION BY USER 'B'
K= YA XB mod q
It can be easily be proved that the key K generated by this algorithm by both parties are the same.

CONCLUSION

In this paper, we design a security to the protocol
to provide reliable efficient data transfer. Here we
implement the Ad hoc On Demand Distance
Vector protocol and provide the security by using
Asymmetric technique. The AODV network
protocol establish at the time of broadcasting. To
prevent the data loss and misuse of data we have
implemented the security using Asymmetric
technique. The encryption and decryption are used
for the security in AODV protocol. The
Asymmetric technique uses the RSA algorithm
encryption method for the encoding of the data to
be sent. For more security reason we are using the
diffie helman algorithm for only the key exchange
at the sender and destination node. Thus with the
use of broadcasting methods of AODV the

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 76

ISSN 2229-5518

network is established and data packets are sent to the destination nodes.

REFERENCES

[1] Bingwen He, Joakin Hagglund, QingGu: Security in Ad hoc Network.http://www.cse.fau.edu/~jie/research/pub lications/Publication_files/SecureRouting.pdf.
[2] C. E. Perkins and P. Bhagwat, “Highly Dynamic Destination-Sequenced Distance-Vector Routing (DSDV) for Mobile Computers,” In Proc. Of SIGCOMM 1994.
[3] Charles E. Perkins and Elizabeth M. Royer, “Ad-Hoc On Demand Distance Vector Routing,” In Proc. 2nd IEEE Workshop on Mobile ComputingSystems and Applications, pages 90–100, IEEE Computer Society,February 1999.
[4] Cha, J.C., & Cheon, J.H. (2003). An identity- based signature from gap Diffie- Hellman groups. In Proceedings of Public Key Cryptography (pp. 18-
30).(Sym crypt)
[5] CMU Monarch Group, “CMU Monarch
extensions to the NS-2 simulator,
“http://monarch.cs.cmu.edu/cmu-ns.html.
[6] D. B. Johnson and D. A. Maltz, “Dynamic
Source Routing,” in Ad Hoc Wireless Networks,

Mobile Computing, T. Imielinski and H. Korth

(Eds.),Chapter 5, pp. 153–181, Kluwer Academic
Publishers, 1996.
[7] Hu, Y., Johnson, D., & Perrig, A. (2002). SEAD:
Secure Efficient Distance Vector Routing in Mobile
Wireless Ad-Hoc Networks. Proc. of the 4th IEEE

Workshop on Mobile Computing Systems and

Applications (WMCSA'02) (pp. 3-13).

[8] Hu, Y., Perrig, A., & Johnson, D. (2002).
Ariadne: A Secure On-Demand Routing for Ad
Hoc Networks.Proc. of MobiCom 2002, Atlanta.
[9] I. D. Chakeres and E. M. Belding-Royer, “The
Utility of Hello Messages for Determining Link
Connectivity,” in Proceedings of the International

Symposium on Wireless Personal Multimedia

Communications (WPMC), Honolulu, Hawaii,

October 2002, pp. 504–508.
[10] Gustav J. Simmons. Symmetric and
Asymmetric encryption. ACMComputing surveys
(CSUR). Volume 11, Issue 4 pp 305-330, Dec 1979.
[11] M. Zapata and N. Asokan, “Securing Ad-hoc
Routing Protocols,” in Proc. of ACM Workshop on

Wireless Security (WiSe), Atlanta, GA, Sept. 2002.

[12] M. F. Juwad, and H. S. Al-Raweshidy,
“Experimental Performance Comparisons between

SAODV & AODV”, IEEE Second Asia International

Conference on Modelling & Simulation,
2008
[13] Junaid Arshad and Mohammad Ajmal Azad, “Performance Evaluation of Secure on-Demand Routing Protocols for Mobile Ad-hoc Networks”,
1-4244-0626-9/06 © 2006 IEEE
[14] Davide Cerri and Alessandro Ghioni,
“Securing AODV: The A-SAODV Secure Routing

Communications Magazine, February 2008
www.cse.scu.edu/~tschwarz/coen350/diffiehellman .ht

ml - United States