Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 1
ISS N 2229-5518
A Novel Algorithm of Super-Spatial Structure Pre- diction for RGB Colourspace
C.S.Rawat, Seema G Bhateja, Dr. Sukadev Meher
—————————— ——————————
THE key in efficient image compr ession is to explor e sour ce corr elation so as to find a compact r epr esentation of im-
age data. Existing lossless image compr ession [1], [2] schemes attempt to pr edict image data using their spatial neighbor- hood [1]. A natural image often contains a lar ge number of structur e components, such as edges, contours, and textur es. These structur e components may r epeat themselves at various locations and scales. Ther efor e, ther e is a need to develop a mor e efficient image pr ediction scheme to exploit this type of image corr elation.
The idea of impr oving image pr ediction and coding effi- ciency by r elaxing the neighborhood constraint can be tr aced back to sequential data compr ession [4] and vector quantiza- tion for image compr ession. In sequential data compr ession, a substring of text is r epr esented by a displacement/length r ef- er ence to a substr ing pr eviously seen in the text. Stor er ex- tended the sequential data compr ession to lossless image compr ession. How ever, the algorithm is not competitive w ith the state-of-the-art such as context -based adaptive lossless image coding (CALIC)[1] in terms of coding efficiency. Dur ing vector quantization (VQ) for lossless image compr ession, the input image is processed as vector s of image pixels. The en- coder takes in a vector and finds the best match fr om its stor ed codebook. The addr ess of the best match, the r esidual betw een the or iginal vector and its best match ar e then transmitted to the decoder. The decoder uses the addr ess to access an iden- tical codebook, and obtains the r econstructed vector. Recently, r esearchers have extended the VQ method to visual pattern image coding (VPIC) and visual pattern vector quantization (VPVQ). The encoding per formance of VQ-based methods lar gely depends on the codebook design. These methods still
———— ——— ——— ——— ———
C.S.Rawat is pursuing Phd in ECE Dept., NIT Rourkela. E-
Dr. Sukadev Meher is currently working as Prof. and Head of ECE Dept,
NIT Rourkela.
suffer fr om low er coding efficiency, w hen compar ed w ith the
state-of-the-art image coding schemes.
In the intra pr ediction scheme pr oposed by Nokia, ther e
ar e ten possible pr ediction methods: DC pr ediction, dir ecti on- al extrapolations, and block matching. DC and dir ectional pr ediction methods ar e very similar with those of H.264 intra pr ediction [3]. The block matching tries to find the best match of the cur r ent block by sear ching w ithin a certain range of its neighbor ing blocks. This neighborhood constr aint will limit the image compr ession efficiency since image str uctur e com- ponents may r epeat themselves at var ious locations.
In fr actal image compr ession [4], the self-similarity b e-
tw een differ ent parts of an image is used for image compr es- sion based on contr active mapping fixed point theor em. How- ever , the fractal image compr ession focuses on contr active transfor m design, which makes it usually not suitable for loss- less image compr ession. Mor eover, it is extr emely computa- tionally expensive due to the sear ch of optimum tr ansfor ma- tions. Even w ith high complexity, most fractal-based schemes ar e not competitive w ith the curr ent state of the art [1].
An efficient image compr ession scheme based on super-
spatial str uctur e pr ediction of str uctur e units is pr esented her e. A natur al image can be often separ ated into two types of image r egions: str uctur e and non-str uctur e r egions. Nonstruc- tur e r egions, such as smooth image ar eas, can be efficiently r epr esented with conventional spatial transforms, such as KLT (Karhunen Lòeve transform), DCT (discr ete cosine transform) and DW T (discr ete wavelet transform). How ever , str uctur e r egions, which consist of high fr equency str uctur al comp o- nents and curvilinear featur es in images, such as edges, con- tours, and textur e r egions, cannot be efficiently r epr esented by these linear spatial transfor ms. They ar e often har d to com- pr ess and consume a majority of the total encoding bit rate.
Super-spatial str uctur e pr ediction br eaks the neighbor hood constr aint, attempting to find an optimal pr ediction of stru c- tur e components [5], [6] within the pr eviously encoded image r egions. It borr ows the idea of motion pr ediction fr om video coding, which pr edicts a block in the curr ent frame using its pr evious encoded frames. In order to “enj oy the b est of b oth wor lds”, a classification scheme is used to par tition an image into tw o types of r egions: structure regions (SRs) and nonstruc- ture regions (NSRs). Str uctur e r egions ar e encoded with super- spatial pr edict ion while NSRs can be efficiently encoded w ith conventional image compr ession methods, such as CALIC. It
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 2

ISS N 2229-5518
is also important to point out that no codebook is r equir ed in this compr ession scheme, since the best matches of str uctur e components ar e simply sear ched w ithin encoded image r e- gions.
This paper is or ganized as follows:
Section 2 expalins the algorithm used to pr edict the image us- ing dir ect pr ediction method wher ein an optimal pr ediction of structur e components is done within the pr eviously encoded image r egions. Also gives an explanation for differ ent modes
that can be used for pr ediction of image blocks. Section 3 ex- plains the r esidue encoding scheme used which helps in r e- tr ieving the lossless image at the decoder . Section 4 gives detail about compr essing the nonstr uctur al ar eas using CAL- IC. The block diagram of the complete algor ithm is given in next section and at the end simulation r esults in RGB Colorspace is given, w her e the algorithm was tested.
A r eal wor ld scene often consists of various physical ob-
j ects, such as buildings, tr ees, grassland, etc. Each phy sical
obj ect is constructed fr om a lar ge number of structur e comp o-
nents based upon some pr edeter mined obj ect character istics. These str uctur e components may r epeat themselves at various locations and scales Fig. 1. Ther efor e, it is important to exploit this type of data similar ity and r edundancy for efficient image coding.
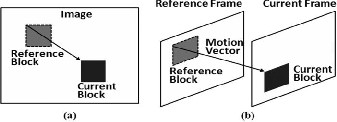
The Super Spatial Str uctur e Pr ediction borr ows its idea
fr om motion pr ediction [3] Fig.2 . In motion pr ediction Fig.
2(b), w e search an ar ea in the r efer ence frame to find the best
match of the curr ent block, based on some distortion metric.
The chosen r efer ence block becomes the pr edictor of the cur- r ent block. The pr ediction r esidual and the motion vector ar e then encoded and sent to the decoder. In similar str uctur e block pr ediction Fig.2(a), w e search within the pr eviously en- coded image r egion to find the pr ediction of an image block. The r efer ence block that r esults in the minimum block differ- ence is selected as the optimal pr ediction. For simplicity, we use the sum of absolute differ ence (SAD) to measur e the block differ ence.
(a) Barbara imag e. (b) Fo ur imag e bloc ks e xtrac te d fro m Barbara
Fig . 1 Example fo r S upe r-S patial S truc ture Block Re dundanc ie s
Fig .2. (a) S upe r-S patial struc ture pre dic tio n. (b) Mo tio n pre dic tio n in v ideo co ding .
As in video coding [3], w e need to encode the position infor- mation of the best matching r efer ence block. To this end, we simply encode the hor izontal and vertical offsets, between the coor dinates of the curr ent block and the r efer ence block using context-adaptive arithmetic encoder. The size of the pr ediction unit is an important par ameter in the similar str uctur e block pr ediction. When the unit size is small, the amount of pr edic- tion and coding over head will b ecome very lar ge. How ever, if we use a lar ger pr ediction unit, the overall pr ediction efficien- cy will decr ease. In this wor k, w e attempt to find a good tra- deoff between these tw o and pr opose to per form spatial image pr ediction on block basis.
A block-based image classification scheme is used her e. The image is par titioned into blocks of 8x8. We then classify these blocks into two categor ies: structur e and nonstr uctur e blocks. Structur e blocks ar e encoded with super-spatial pr edic- tion. Nonstr uctur e blocks ar e encoded with conventional loss- less image compr ession methods, such as CALIC.
2.2 Estimation of Threshold
The thr eshold is r equir ed while compar ing the curr ent block w ith the pr evious encoded r egion. This thr eshold value should be so decided that it w ill give best compr ession per- formance.
2.3 Prediction Modes
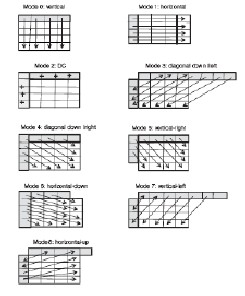
In this scheme using 4 × 4 blocks, nine modes of pr edi ction ar e suppor ted. A 4 × 4 b lock of pixels lab eled “a” thr ough “p” ar e pr edicted fr om a r ow of eight pixels lab eled “A” thr ough “H” ab ove the curr ent block and a col
umn of four pixels lab eled “I” thr ough “L” to the left of the
curr ent b lock as w ell as a cor ner pixel lab eled “M,” as shown
in Fig 3. The nine modes of 4 × 4 blocks ar e mode 0 (vertical pr ediction), mode 1 (hor izontal pr ediction), mode 2 (DC pr e- diction), mode 3 (diagonal down/left pr ediction), mode 4 (d i- agonal down/r ight pr ediction), mode 5 (vertical-r ight pr edic- tion), mode 6 (hor izontal-down pr ediction), mode 7 (ver tical- left pr ediction), and mode 8 (hor izontal-up pr ediction). Out of the nine modes the mode that r esults in minimum SAD is the chosen block.
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 3
ISS N 2229-5518
as a str uctur e block. Otherwise, it is classified as a nonstruc- tur e block.
Fig .3 Nine mo de s o f Pre dic tio n use d
The implemented image compr ession scheme is pur ely lossless, the r esidues need to be tr ansmitted along with the image. But this w ill incr ease the payload size and thus the compr ession will not be achieved successfully. The r esidues ar e encounter ed in two places: - The CALIC Algor ithm and the SAD r esidues. Ar ithmetic coding [7], [8] schemes ar e to be used to tr ansmit the r esidues to further r educe the size of the overhead data per block.
Ar ithmetic coding is especially useful when dealing with
sour ces w ith small alphabets, such as binary sour ces, and a l- phabets w ith highly skew ed pr obabilities. It is also a very us e- ful appr oach w hen, for various r easons, the modeling and coding aspects of lossless compr ession ar e to be kept separ ate. In arithmetic coding a unique identifier or tag is generated for the sequence to be encoded. This tag corr esponds to a binary fr action, w hich becomes the binary code for the s equence.
In or der to distinguish a sequence of symbols fr om an other
sequence of it has to be tagged w ith a unique identifier. One
possible set of tags for r epr esenting s equences of symbols ar e the numbers in the unit interval (0, 1). Because the number of
The Context Adaptive Lossless Image Codec (CALIC)
scheme, uses both context and pr ediction of the pixel values.
CALIC employs a two-step (pr ediction/r esidual) appr oach. In the pr ediction step, CALIC [1] employs a simple new gradient based non-linear pr ediction scheme called GAP (gradient- adj usted pr edictor ) w hich a dj usts pr ediction coefficients based on estimates of local gradients. Pr edictions then made context- sensitive and adaptive by modeling of pr ediction err or s and feedback of the expected err or conditioned on pr oper ly chosen modeling contexts. The modeling context is a combination of quantized local gradient and textur e pattern, two featur es that ar e indicative of the err or behavior. The net effect is a non- linear , context-based, adaptive pr ediction scheme that can cor- r ect itself by learning fr om its own past mistakes under differ- ent contexts.
CALIC encodes and decodes images in raster scan or der
with a single pass thr ough the image. The coding pr ocess uses
pr ediction templates that involve only the pr evious tw o scan lines of coded pixels. Consequently, the encoding and decod- ing algorithms r equir e a simple double buffer that holds two r ows of pixels that immediately pr ecede the curr ent pixel, hence facilitating sequential build-up of the image.
In the continuous-tone mode of CALIC, the system has four
major integrated components: -
Pr ediction
Context selection and quantization
Context modeling of pr ediction err ors
Entr opy coding of pr ediction err ors.
CALIC is a spatial pr ediction based scheme, in which GAP is used for adaptive image pr ediction [1].
Her e GAP pr ediction is per formed on the original image and
the pr ediction err or for each block is computed. If the pr edi c- tion error is lar ger than a given thr eshold, then it is consider ed
number s in the unit interval is infinite, it should be possibl e to
assign a unique tag to each distinct sequence of symbols. In or der to do this w e need a function that will map s equences of symbols into the unit interval. A function that maps random var iables, and sequences of r andom var iables, into the unit interval is the cumulative distribution function (cdf) of the random var iable associated with the source. This is the fun c- tion to be used in developing the ar ithmetic code.
The complete algor ithm used for this lossless image com- pr ession scheme can be categor ized into tw o main parts as listed below.
The or iginal image is subj ected to Similar Str uctur e Block Pr ediction Algor ithm. This pr oduces a Lossy Compr essed Image and a set of r esidues. The r esidues ar e then encoded using Ar ithmetic Coding. The Lossy Compr essed Image along w ith the encoded r esidues for ms the compr essed data as shown in Fig. 4.
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 4


ISS N 2229-5518
ORIGINAL IMAGE
SIMILAR STRUCTURE BLOCK PREDICTION
(Each R, G and B com-
ponent
RESIDUES
LOSSY COM- PRESSED IMAGE
ARITHMETIC
ENCODER COMPRESSED
DATA
Fig . 4 Pro po se d Enco de r

The compr essed data consisting of Lossy Compr essed Im- age and encoded r esidues is then given as inputs to the d e- coder. The encoded r esidues ar e given to the Ar ithmetic De- coder to obtain the or iginal set of r esidues which is then add- ed to the Lossy Compr essed Image to r econstruct the Final Image as shown in Fig. 5.
COMPRESSED DATA
ENCODED
Fig .6 S tandard RGB Colo rsapce Test Imag e s use d
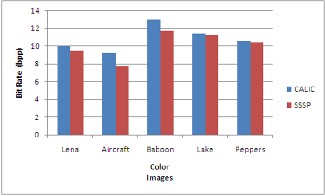
The RGB Colorspace images ar e first divided into each R, G and B component and individually the algor ithm is applied into each component. The bit rate for the compr essed color image is calculated and as shown in gr aph 1.
In graph 1, Bit rate of pr oposed algorithm is compar ed w ith
CALIC for each test images . From graph w e can ob serve that bit r ate saving is mor e for baboon which has mor e str uctural r egions.
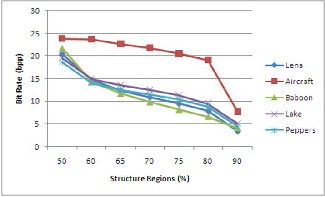
The graph 2 shows the var iation of bit rate for differ ent per-
centage of str uctural r egions for all test images. The r esult shown in gr aph 1 is the best case r esult when comparing w ith CALIC w hich has been obtained while changing the per cen- tage of structur e r egions as shown in gr aph 2.
LOSSY COM- PRESSED IMAGE
LOSSLESS RECON- STRUCTED IMAGE
RESIDUES
ARITHMETIC DECODER
DECODED RESIDUES
Fig . 5 Pro po se d Deco de r
All the simulations w er e done using MATLAB 7.11 (R2010b)
on RGB Color spaces on standard Images (Fig 6) size of
512x512 pixels like Lena, Air craft, Baboon, Lake and Pepper s.
Graph 1 Compression Performance comparison of SSSP with CALIC
Graph 2 Variation of Bit Rate with the percentage of Structure
Regions
In this endeavor a simple yet efficient lossless image compr es- sion algorithm based on structur e pr ediction has been success- fully designed and tested for RGB Colorspace. It is motivated by motion pr ediction in video coding, attempting to find an
IJSER © 2012
Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h, Vo lume 3, Issue 2, February -2012 5
ISS N 2229-5518
[14] Mauro Barni, “Doc ume nt and Imag e Co mpressio n”, Tay lo r and
Franc is, 2006.
[15] Rafae l Go nzale z & Ric hard Woo ds, “Dig ital Imag e Proce ssing using
MATLAB”, Tata McGraw Hill, 2010.
optimal pr ediction of a str uctur e components w ithin pr evious- ly encoded image r egions. Taking CALIC as the base code, the image was classified into various r egions and they w er e en- coded accor dingly. The extensive exper imental r esults demon- strate that the pr oposed hybr id scheme is very efficient in loss- less image compr ession, especially for images with significant structur e components.
[1] X. Wu and N. Memon, ― Context-based, adapt ive, lossless image coding,‖
IEEE Trans. Commun., vol. 45, no. 4, pp. 437–444, Apr. 1997.
[2] M. J. Weinberger, G. Seroussi, and G. Sapiro, ―The LOCO -I lossless image compression algorithm: Principles and standardization into JPEG-LS,‖ IEEE Trans. Image Process., vol. 9, no. 8, pp. 1309–1324, Aug. 2000.
[3] T. Wiegand, G. J. Sullivan, G. Bjntegaard, and A. Luthra, ―Overview
of the H.264/AVC video coding standard,‖ IEEE Trans. Circuits Syst. Video Technol., vol. 13, no. 7, Jun. 2003.
[4] B. Wohlberg and G. de Jager, ―A review of the fractal image coding literature,‖ IEEE Trans. Image Process., vol. 8, no. 12, pp. 1716–1729, Dec. 1999.
[5] Xiwen Zhao and Zhihai He,‖ Local Structure Learning and Predic-
tion for Efficient Lossless Image Compression‖, 2010 IEEE, pp. 1286-
1289.
[6] Xiwen OwenZhao, and Zhihai HenryHe,‖ Lossless Image Compres- sion Using Super-Spatial Structure Prediction‖, IEEE SIGNAL PROCESSING LETTERS, VOL. 17, NO. 4, APRIL 2010, pp. 383 -386.
[7] David Salomon, “Data Compression: A Complete Reference”,3rd Edi-
tion, Springer, 2007.
[8] Khalid Sayood, “Introduction to Data compression”, 3rd Edition, El- seiver Publications, 2006.
[9] X. Wu, “Lossless compression of continuous-tone images via context selec- tion, quantization, and modeling”, IEEE Trans. Image Processing,Vol.6, No.5 (pp.656-664) 1997.
[10] S till Imag e and V ideo Co mpre ssio n with Matlab, by K.S. Thy ag ara-
jan, a Jo hn Wiley & So ns, Inc , Public atio n.
[11] Hao Hu, “A S tudy o f CALIC”, A pape r submitte d to the Co mpute r Scie nce & Elec tric al Eng inee ring De partme nt at Univ e rsity o f Mary- land Balti mo re Co unty , Dece mbe r 2004.
[12] Grzego rz Ulac ha, and Ry szard S tasiński, “Effe c tive Co nte xt Lossle ss Imag e Co ding Appro ac h Base d o n Adaptiv e Pre dic tio n”, Wo rld Ac ade my o f Sc ie nce, Eng inee ring and Tec hno logy, 2009.
[13] F. Wu and X. S un, “Imag e co mpressio n by v isual patte rn vec to r
quantizatio n (VPVQ),” in Proc. IEEE Da ta Compression Conf.
(DCC’2008), pp. 123–131.
IJSER © 2012