International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 207
ISSN 2229-5518
A Case Study Of Non-Technical Instituions-DEA Approach
Dr.R.P.Sreedevi
Abstract— In this paper we apply DEA techniques to evaluate the comparative efficiency of 25 Non –Minority Technical Institutions Under JNTUH, Andhra Pra- desh. By using three inputs and two outputs at the institutional-level, we are able to identify the most technically efficient institutions that may work as benchmark in the sector. The results suggest that a great portion of institutions may be working inefficiently, contributing to a significant waste of resources. Technical Institutions are playing an important role in making India a knowledge hub of this century. There is still great diversity in their relative performance, which is matter of concern to the education planner. This article employs the method of data envelopment analysis (DEA) to compare the relative efficiency. The identification of the strongest and the weakest parameters of various Technical institutions could be very useful in improving their efficiency and performance. DEA is essentially an optimization algorithm, which develops efficiency scores for all DMUs on a scale of zero to 100%, with units receiving 100% efficiency score being called efficient.
Index Terms— DEA, DMUS,CCR Model, Technical Education,Technical Efficiency Score, Ranks, Peer count
—————————— ——————————
1 INTRODUCTION
The concept of efficiency is an essential part of the process of evaluating the performance of technical institutions which consist of three main components: efficiency, effectiveness and productiv- ity. The efficiency is an expression of the success of the production unit in tightening the relationship between resources used and outputs in an efficient manner designed to maximize output and reduce input. The efficiency is an expression of the success of the production unit in achieving its objectives through the compari- son between planned objectives and what has already been achieved. Hence, the concept of economic efficiency of higher education includes two types of efficiency: Technical Efficiency which means the ability of the institution to produce the maxi- mum amount of production using available inputs and the func- tional efficiency or allocative efficiency which refers to the ability of the institution to use the optimal mix of inputs, taking into ac- count the prices of these inputs and production techniques avail- able. Thus, the overall economic efficiency means the ability of educational institutions to achieve technical efficiency. There are other studies that add another type of efficiency, especially when analyzing the efficiency of institutions of higher education which is the dynamic efficiency and that relate to the ability of the insti- tution to innovate in production methods.
2. Back ground
Throughout the literature, it is well recognized that DEA is at- tributed to the seminal work of Charnes, et al. (1978) while SFA is jointly due to Aigner, et al. (1977) and Meeusen and van der Broech (1977). Contributions in further developing the approach- es since those beginnings are numerous and well documented elsewhere. That need not be repeated here. Rather, methodologi- cal advancements along with empirical applications and imple- mentation issues are provided by Cooper, et al. (2007) and Cook and Zhu (2008) for DEA and by Coelli, et al, (2005) and Kumbhakar and Lovell (2003) for SFA. These works are further supported by some 4000 published DEA research papers (Em-
rouznejad, et al., 2008). That volume of literature cannot be re- viewed here. Instead, the following presents an overview of the empirical literature pertaining to DEA and SFA comparative effi- ciency estimates. That subset of the literature appears to consist of eight studies only one of which is an application of both DEA and SFA to higher education. The studies are wide in variety and in- vestigate the operating efficiencies of Hawaiian swine farms (Sharma et al., 1997), Dutch dairy farms (Reinhard, et al., 1999), Bangladesh farms (Wadud and White, 2000), United Kingdom hospitals (Jacobs, 2001), English Channel fisheries (Tingley, et al.,
2005), Canadian universities (McMillan and Chan, 2006), Greek dairy farms (Theodoridis and Psychoudakis, 2008), and Indian leather companies (Bhandari and Maiti, 2011). These studies rely on the basic idea that efficiency is based on firms producing the maximum output for a given set of inputs. A corresponding pro- duction frontier exists. Efficiency scores range from zero to one with the latter referring to efficient firms resting on the frontier while inefficient firms lie below th frontier with scores below the value of one. In the Hawaiian swine farm study by Sharma, et al. (1997), mean efficiency estimates range from 0.64 under DEA es- timation to 0.75 under SFA estimation. In the evaluation of Dutch dairy farms, Reinhard, et al., (1999) develop models of both tech- nical and environmental efficiencies and find a mean efficiency range of 0.44 to 0.89. For Bangladesh farms, Wadud and White (2000) find that mean efficiencies vary between 0.79 using DEA and 0.86 using SFA. For UK hospitals, a host of different model specifications employed by Jacobs (2001) generated mean efficien- cies ranging from 0.65 under DEA to 0.88 under SFA. The Tingley, et al. (2005) investigation of three different fishing fleets results in DEA vs. SFA efficiency estimates ranging from 0.56 to 0.65, 0.63 to
0.76, and 0.61 to 0.79. McMillan and Chan (2006) evaluated the
operating efficiencies of 45 Canadian universities. In using differ- ent variables to define four DEA and four SFA models, the effi- ciency estimates range from an average of 0.91 to 0.98 under the DEA versions and from 0.89 to 0.95 under the SFA versions. The study by Theodoridis and Psychoudakis (2008) reports Greek dairy farm efficiencies on the order of 0.63 and 0.68 using DEA
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 208
ISSN 2229-5518
and 0.81 using SFA. A single comparative evaluation was not possible for the Bhandari and Maiti (2011) study of Indian leather companies. They present multiple specifications by year over sev- en years. Using an average of their 2002-03 results, there appears to be a 0.55 efficiency arising from DEA estimation and a 0.83 average efficiency derived from SFA estimation. In summary, the average estimated efficiencies range from a low of 0.44 under
DEA estimation to a high of 0.98 using a SFA model. The mini- mum efficiency difference was found to be 0.07 while the maxi- mum difference was more than six times greater at 0.45. The stud- ies by Reinhard, et al., (1999), Wadud and White (2000), and McMillan and Chan (2006) indicate that DEA relative to SFA technical efficiencies are somewhat greater. The remaining five studies find greater efficiency scores in using SFA as opposed to DEA. However, the results come from eight different industries housed in seven different countries. In addition, each study uses a different set of variables, employs different times, and performs the analysis under different model specifications.
3. Data Envelopment Analysis
The Data Envelopment Analysis (DEA) means by which efficiency of like institutions can be effectively ranked and ordered in terms of their relationship to a best practice standard. In the case of non- parametric technique, DEA, the best practice standard is the most efficient institution(s) in the group while with the parametric es- timation technique, a best practice (maximum output attainable) frontier is estimated. With DEA, there will always be some institu- tions that aredeemed to be on the frontier while with SFA, none of the institutions need to be on the frontier (Johnes, 2003).DEA does not allow hypothesis testing and assumes that every observation unit operates under the same technology. It treats individual dif- ferences as fixed, ignoring the possibility to be random (Horne and Hu,2005).With DEA, frontiers are constructed so that they can envelop the observed data points using a linear programming methodology. In this approach, the efficiency of a firm is meas- ured relative to the efficiency of all firms, subject the restriction that all firms are on or below the frontier (Cruz, 2003).Efficient points are defined to be the best-practice frontier. Nonetheless, points below the best-pra ctice frontier are the inefficient points. The distance of a point below the frontier reveals the inefficiency of that observation. With DEA, assumptions are made such that random influences are less of an issue, multiple -output produc- tion is important, prices are difficult to define and behavioral as- sumptions such as cost minimization or maximization are difficult to justify (see Coelli, Rao, Battese, 1998).
4. CCR Model
The CCR model which was initially proposed by Charnes, Cooper and Rhodes in 1978. Tools and ideas commonly used in DEA are also introduced and the concepts developed and extend- ed. There, for each DMU, we formed the virtual input and output by (yet unknown) weights {vi) and (ur)'
Virtual input = vixio-\- • • • -\- VmXmo
Virtual output = uiyio + • • • + Ugyso
Then we tried to determine the weight, using linear programming so as to maximize the ratio
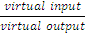
The optimal weights may (and generally will) vary from one DMU to another DMU. Thus, the "weights" in DEA are derived from the data instead of being fixed in advance. Each DMU is assigned a best set of weights with values that may vary from one DMU to another.
Suppose there are n DMUs: DMUi, DMU2,..., and DMU„. Some common input and output items for each of these j = l,...,n DMUs are selected as follows:
1. Numerical data are available for each input and output, with the data assumed to be positive for all DMUs.
2. The items (inputs, outputs and choice of DMUs) should reflect an analyst's or a manager's interest in the components that will enter into the relative efficiency evaluations of the DMUs.
3. In principle, smaller input amounts are preferable and larger
output amounts are preferable so the efficiency scores should reflect these principles.
4. The measurement units of the different inputs and outputs
need not be congruent. Some may involve number of persons, or areas of floor space,money expended, etc.
5. Emperical Investigation
The efficiency score of DMUS 2,9,10,11,12, 17, 18, 19 is 1.000. To measure over all input technical efficiency implicity we have assumed that environment is scale efficient and these are no non- performing assess, when these conditions are imposed, consequently the institutions arises with 100 percent of technical efficiency. The Efficiency score of DMU 1 is 0.978, It is nearer to attain 100 percent efficiency score. If returns to scale are constant it could have produced its current outputs 0.98 percent of inputs. It means 0.02 percent of inputs are freely disposed. DMU 13 had the least efficiency score is 0.705 ≈ 0.71, it attained only 71 percent of inputs to produce its current outputs and 19 percent of inputs are cost lessly disposed. DMUS
7(0.934),8(0.901),14(0.946),21(0.940),22(0.947),25(0.962) attained above 90% over all technical efficiency. Ranks will be allotted based on peer count. The Efficient DMUs will be awarded ranks based on their peer count. The Efficient DMU with highest peer count will be awarded first, the next highest will be second as it follows.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 209
ISSN 2229-5518
Table: Technical Efficiency Score
& Ranks of DMUS
DMUS | Technical Efficiency | Ranks |
1 | 0.978 | |
2 | 1.000 | 1 |
3 | 0.892 | |
4 | 0.769 | |
5 | 0.865 | |
6 | 0.830 | |
7 | 0.934 | |
8 | 0.901 | |
9 | 1.000 | 3 |
10 | 1.000 | |
11 | 1.000 | |
12 | 1.000 | 4 |
13 | 0.705 | |
14 | 0.946 | |
15 | 0.889 | |
16 | 0.885 | |
17 | 1.000 | |
18 | 1.000 | |
19 | 1.000 | 2 |
20 | 0.865 | |
21 | 0.940 | |
22 | 0.947 | |
23 | 0.962 | |
24 | 0.874 | |
25 | 0.905 | |
6. Conclusion
The core aim of the technical education policy in any country is establishing a competitive, qualitative higher education with effi- ciently operating institutions. The question of efficiency needs increased attention not only because of the decline of the state support but also the rapid rise of the student mass. In the educa- tion system, especially higher education, it’s not easy to measure its efficiency. The situation is more complicated since those insti- tutions have multiple inputs and outputs. In this case, a possible method of determining efficiency is Data Envelopment Analysis. In this paper I adopted the two stage efficiency analysis and used it to compare the efficiency of 25 Non-Minority Technical Institu- tions in JNTUH, Andhra Pradesh . And then I used the to bit re- gression to determine the most environmental factors that affect the efficiency of this institutes. The analysis shows that the most influential factors affecting efficiency are the growth rate, private share, and public expenditure on education. The main results of the model are the negative impact of technical education and eco- nomic growth on technical education efficiency, while there is positive relationship between government expenditure on educa- tion and technical education efficiency.
7. References
[1] Aigner, D. J., Lowell, C. A. K. & Schmidt, P. (1977). Formula- tion and estimation of stochastic frontier production function models. Journal of Econometrics, 6(1), 21-37.
[2] Banker, R. D., Charnes, A. & Cooper, W. W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30, 1078-1092.
[3] Battese, G. E. & Coelli, T. J. (1992). Frontier production func- tions, technical efficiency and panel data: with application to paddy farmers in India. Journal of Productivity Analysis, 3(1/2),
153-169.
[4] Bhandari, A. K. & Maiti, P. (2011). Efficiency of the Indian
leather firms, some results obtained using the two conventional methods. Journal of Productivity Analysis, 37(1), 73-93.
[5] Charnes, A., Cooper, W. W. & Rhodes, E. (1978). Measuring the efficiency of decision-making units. European Journal of Opera- tional Research, 2(6), 425-444.
[6] Coelli, T., Prasada, J. D., Rao, S., O’Donnell, C. J. & Battese, G. E. (2005). An Introduction to Efficiency and Productivity Analysis. Springer, New York.
Cook, W. D. & Zhu, J. (2008). Data Envelopment Analysis. Wade
D. Cook and Joe Zhu.
[7] Cooper, W., Seiford, L. & Tone, K. (2007). Data Envelopment
Analysis, Springer, New York. 452
Emrouznejad, A., Parker, B. R. & Tavares, G. (2008). Evaluation of
research in efficiency and productivity: A survey and analysis of the first 30 years of scholarly literature in DEA. Socio-Economic Planning Sciences, 42(3), 151-157.
[8] Jacobs, R. (2001). Alternative methods to examine hospital effi- ciency, Data envelopment analysis and stochastic frontier analy- sis. Health Care Management Science, 4(2), 103-115.
[9] Kumbhakar, S. C. & Lovell, C. A. K. (2003). Stochastic Frontier
Analysis. Cambridge University Press, Cambridge..
[10] Martin, J. C. & Roman, C. (2006). A benchmarking analysis of Spanish commercial airports. A comparison between SMOP and DEA ranking methods. Networks and Spatial Economics, 6(2 ), 111-
134.
[11] Meeusen, W. & van-den-Broech, J. (1977). Efficiency from Cobb-Douglas production functions with composed error. Interna- tional Economic Review, 18(2), 435-444.
[12] McMillan, M. L. & Chan, W. H. (2006). University efficiency, a comparison and consolidation of results from stochastic and non- stochastic methods. Education Economics, 14, 1-30.
[13] Reinhard, S., Knox Lovell, C. A. & Thijssen, G. (1999). Econ- ometric estimation of technical and environmental efficiency, an application to Dutch dairy farms. American Journal of Agricultural Economics, 81(1), 44-60.
[14] Sav, G. T. (2004). Higher education costs and scale and scope economies. Applied Economics, 36(6), 607-614.
[15] Sav, G. T. (2012). Managing operating efficiencies of publicly owned universities: American university stochastic frontier esti- mates using panel data. Advances in Applied Economics and Man- agement, 2(1), 1-23.
[16] Sharma, K. R., Leung, P. & Zaleski, H. M. (1997). Productive
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 210
ISSN 2229-5518
efficiency of the swine industry in Hawaii, Stochastic frontier vs. data envelopment analysis. Journal of Productivity Analysis, 8, 447-
459.
[18] Theodoridis, A. M. & Psychoudakis, A. (2008). Efficiency
measurement in Greek dairy farms, Stochastic Frontier vs. data envelopment analysis. International Journal of Economic Sciences and Applied Research, 1(2), 53-67.
[19] Tingley, D., Pascoe, S. & Coglan, L. (2005). Factors affecting technical efficiency in fisheries, stochastic production frontier versus data envelopment analysis approaches. Fisheries Research
73, 363-376.
[20] Wadud, A. & White, B. (2000). Farm household efficiency in Bangladesh, a comparison of stochastic frontier and DEA meth- ods. Applied Economics, 32(13), 1665-1673.
IJSER © 2013 http://www.ijser.org