International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 11

ISSN 2229-5518

Visco-Elastic MHD Fluid Flow Over a Vertical

Plate with Dufour and Soret Effects

Rita Choudhury and Sajal Kumar Das

Abstract—An analysis of free convective MHD visco-elastic fluid flow with heat and mass transfer over a vertical plate moving with a constant velocity in presence of Dufour and Soret effects has been presented. The fluid is considered to be non-Newtonian characterized by W alters liquid (Model B′). The surface temperature is assumed to oscillate with small amplitude about a non-uniform mean temperature. The system representation is such that

the 𝑥-axis is taken along the plate and 𝑦�-axis is normal to the plate. The equations governing the fluid flow, heat and mass transfer are solved by

perturbation technique. Analytical expressions for velocity, temperature and concentration fields, non-dimensional skin friction coefficient are obtained.

The first-order velocity profile and skin friction coefficient are obtained numerically and illustrated graphically to observe the visco-elastic effects in combination of other flow parameters involved in the solution. It is observed that the flow field is significantly affected by the visco-elastic parameter in comparison with Newtonian fluid flow phenomena. Possible applications of the present study include engineering science and applied mathematics in the context of aerodynamics, geophysics and aeronautics.

Keywords: Dufour and Soret effects, Grashof number, MHD, perturbation technique, Prandtl number, Schmidt number, skin friction, visco-elastic.

——————————  ——————————

1 Introduction

HE investigation of visco-elastic fluid flows over a vertical plate in presence of magnetic field has attracted the researchers for its application in various fields like geophysics, engineering

sciences, astrophysics, biological system, soil physics,
aerodynamics and aeronautics. The study of heat and mass transfer is important because of its wide applications in geothermal and oil reservoir engineering studies. Stokes [1] has studied the effects of internal friction of fluids in the motion of pendulum. Raptis and Kafousis [2] have studied the free convective MHD flow with mass transfer in porous medium with constant heat flux. Jha and Singh [3] have analyzed the Soret effect on free convection with mass transfer in the Stokes problem for an infinite vertical plate. Dursunkaya and Worek [4] have studied the diffusion thermo and thermal-diffusion effects in transient and natural convection and Kafousis and Williams [5] have continued the same for temperature dependant forced convection with mass transfer. Anghel et al. [6] has investigated the Dufour and Soret effects on free convection boundary layer over a vertical surface in porous medium. Aboeldahab and Elbarbary [7] have studied the Hall current effect on MHD free convection past a semi-infinite vertical plate with mass transfer. Megahead et al. [8] have studied the similarity analysis MHD effect on free convection with mass transfer past a semi-infinite vertical plate. Postelincus [9] has analyzed the effect of magnetic field on heat and mass transfer for free convection from vertical surface in porous media with Dufour and Soret effects. Sedeek [10] has investigated the diffusion thermo and thermal diffusion effects on mixed convection with mass transfer in presence of suction and blowing. Chen [11]
has analyzed heat and mass transfer in MHD free convection from a permeable inclined surface with variable temperature. Alam and Rahman [12] have studied the Dufour and Soret effects in MHD free convection with heat and mass transfer past vertical plate in porous medium. Nazmul and Mahmud [13] have studied the Dufour and Soret effects on steady MHD free convection with mass transfer through a porous medium in a rotating system.
Ibrahim et al. [14] have studied the effects of chemical reaction and radiation absorption on the unsteady MHD free convection past a semi-infinite permeable moving plate in presence of heat source. Ananda et al. [15] have investigated the thermal diffusion and chemical effects with simultaneous heat and mass transfer in MHD mixed convection with Ohming heating. Beg and Ghosh [16] have presented an analytical study of MHD radiation convection with surface oscillation and secondary flow effects. Uwanta et al. [17] have studied the radiative convection flow with chemical reaction. Uwanta et al. [18] have also analyzed the MHD free convection over a vertical plate with Dufour and soret effect. Mansour et al. [19] have investigated the effect of chemical reaction and thermal stratification on MHD free convection with heat and mass transfer over a vertical stretching surface in a porous medium in presence of Dufour and Soret effects. Oladapo [20] has studied the Dufour and Soret effects of transient free convection with radiation past a flat moving plate.
In this paper, we have studied the free convective
MHD flow with heat and mass transfer over a vertical plate in presence of Dufour and Soret effect and observe the visco-elastic effects on the fluid flow field along with other flow parameters. The visco-elastic fluid flow is characterized by Walters liquid (Model B′).
The constitutive equation for Walters liquid (Model B′) is

International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 12

ISSN 2229-5518

𝜎𝑖𝑘 = −𝑝𝑔𝑖𝑘 + 𝜎𝑖𝑘 ′, 𝜎′ = 2𝜂 𝑒

𝑖𝑘

− 2𝐾0 𝑒

′𝑖𝑘

(1)
temperature of the fluid, 𝑇𝑚 is the mean temperature of the
where 𝜎𝑖𝑘 is the stress tensor, p is isotropic pressure, 𝑔𝑖𝑘 is
fluid, 𝑇�
is the temperature of fluid at infinity, 𝑇�
is the
the metric tensor of a fixed co-ordinate system xi, vi is the
velocity vector, the contravariant form of e′ik is given by

𝑖𝑘

temperature of the plate, 𝐾𝑟 is the thermal diffusion, 𝐶𝑝 is the specific heat at constant pressure, 𝐶𝑠 is the concentration

𝑒′𝑖𝑘 = 𝜕𝑒

𝜕𝑡

+ 𝑣 𝑚 𝑒𝑖𝑘 ,𝑚
− 𝑣 𝑖 ,𝑚
𝑒𝑖𝑚 − 𝑣 𝑖 ,𝑚
𝑒𝑚𝑘 (2)
susceptibility, 𝐶 is the mass concentration, 𝐶𝑤 is the
It is the convected derivative of the deformation rate tensor
eik defined by
2eik = vi,k +vk,i (3) Here η0 is the limiting viscosity at the small rate of shear which is given by
concentration at the plate surface, C� ∞ is the concentration in
fluid far away from plate, 𝐷 is the molecular diffusivity,
𝐷𝑚 is the coefficient of mass diffusivity and κ is the thermal
conductivity.
The initial boundary conditions are

∞ ∞

𝜂0 = ∫0 𝑁(𝜏)𝑑𝜏 𝑎𝑛𝑑 𝑘0 = ∫0 𝜏𝑁(𝜏)𝑑𝜏
(4)
𝑦� = 0: 𝑢� = 𝑈, 𝑇� = 𝑇�

𝑖𝜔� 𝑡

N(τ) being the relaxation spectrum as introduced by

𝑤 + 𝜀𝑒

(𝑇� �
Walters [21, 22]. This idealized model is a valid approximation of Walters liquid (Model B′) taking very short memories into account so that terms involving
∫∞ 𝜏𝑛 𝑁(𝜏)𝑑𝜏, 𝑛 ≥ 2 (5)
𝑤 − 𝑇∞ ),
𝐶 = 𝐶𝑤 + 𝜀𝑒𝑖𝜔� 𝑡 (𝐶𝑤 − 𝐶∞ )
𝑦� → ∞ ∶ 𝑢� → 0, 𝑇� → 0, 𝐶 → 0 (9)
We introduce the dimensionless quantities

2 � �

0 𝑢 = 𝑢� , 𝑦 = 𝑦�𝑈 , 𝑡 = 𝑡𝑈

, 𝐺

= 𝑔𝛽𝜈(𝑇𝑤−𝑇∞)

have been neglected.

𝑈 𝜈

𝑔𝛽′𝜈(𝐶𝑤−𝐶∞)

𝜈 𝑟

𝜎𝐵0 2 𝜈

𝑈 3 ,

𝜇𝐶𝑝

𝐺𝑚 =

𝑈 3

, 𝑀 =

𝜌𝑈 2

, 𝑃 = ,

𝜅

16𝑎𝜎∗𝜈2 𝑇� 3

𝐷 𝐾 (𝐶 −𝐶 )

𝐷 𝐾 (𝑇� −𝑇� )

2 Mathematical formulation

𝐾2 = ∞

𝑚 𝑟 𝑤 ∞ , 𝑆𝑟 = 𝑚 𝑟 𝑤 ∞

𝜅 𝑈 2 , 𝐷𝑢 = 𝐶 𝐶 𝜈(𝑇� −𝑇� )

𝑇 𝜈(𝐶 −𝐶 )

𝜈 𝜔 � 𝜈

𝑠 𝑝 𝑤

𝑇� −𝑇�∞

∞

𝐶 −𝐶∞

𝑚 𝑤 ∞

The region of unsteady free convective MHD flow of a
𝑆 = , 𝜔 = , 𝜃 =

𝐷 𝑈 2 𝑇�

� , 𝐶 =

. (10)

𝑤−𝑇∞

𝐶𝑤−𝐶∞

visco-elastic electrically conducting fluid characterized by
Walters liquid (Model B′) with heat and mass transfer over
a semi-infinite region perpendicular to a vertical plate,
moving with a constant velocity U, in the presence of
Dufour and Soret effects is considered. The 𝑥-axis is taken along the length of the porous plate and 𝑦�-axis is perpendicular to it. Let 𝑢� be the velocity of the fluid along
𝑥 direction. The surface temperature is assumed to oscillate
with small amplitude about a non-uniform mean
where 𝐺𝑟 is the thermal Grashof number, 𝐺𝑚 is the mass

Grashof number, M is the Hartmann number, 𝐾1 = 0 is
the visco-elastic parameter, 𝐾2 is the thermal radiation
conduction number, 𝑆𝑐 is the Schmidt number, 𝑃𝑟 is the
Prandtl number, 𝑆𝑟 is the Soret number, 𝐷𝑢 is the Dufour
number, 𝜈 is the kinematic viscosity, θ is the dimensionless
temperature, C is the dimensionless concentration.
The thermal radiation flux gradient may be expressed as

𝜕𝑞𝑟

∗ 4 − 𝑇 4 � (11)

temperature. The variation of density with temperature and concentration is considered only in the body force term so that under the above assumption, all the physical quantities
are functions of 𝑦� and �𝑡. The governing equations for the
fluid flow are as follows:

− = 4𝑎𝜎 �𝑇� �

𝜕𝑦

where, q r is the radiative heat flux, 𝑎 is the absorption
coefficient of the fluid and 𝜎* is the Stefan-Boltzmann
constant.
By Taylor’s expansion, we get
𝑇� 4 = 4𝑇� 3𝑇� − 3𝑇� 4 (12)

∞ ∞

momemtum equation:
Using (10) to (12) in (6) to (8), we get

𝜕𝑢 = 𝜕2 𝑢

𝜕3 𝑢

+ 𝐺 𝜃 − 𝑀𝑢 + 𝐺
𝐶 (13)

𝜕𝑢� = 𝜈 𝜕2 𝑢�

𝐾0

𝜕3 𝑢�

𝜎𝐵0 2 𝑢�

𝜕𝑡

𝜕𝑦2 − 𝐾1 𝜕𝑡𝜕𝑦2 𝑟 𝑚

𝜕𝑡

𝜕𝑦�2 − 𝜌 𝜕𝑡𝜕𝑦�2 + 𝑔𝛽(𝑇� − 𝑇� 𝜌

+ 𝛽(𝐶 − 𝐶∞ ) (6)

𝜕𝜃 = 1 𝜕 𝜃

𝜕2 𝐶

𝜕𝑡

𝑃 𝜕𝑦2 − 𝐾2 𝜃 + 𝐷𝑢 𝜕𝑦2 (14)

𝜕𝐶

1 𝜕2 𝐶

𝜕2 𝜃

energy equation:

= + 𝑆 (15)

𝜕𝑡 𝑆𝑐 𝜕𝑦2 𝜕𝑦2

The relevant boundary conditions are

𝜕𝑇� = 𝜅

𝜕2 𝑇�

1 𝜕𝑞𝑟

𝐷𝑚 𝐾𝑟 𝜕2 𝐶

𝑦 = 0: 𝑢 = 1 , 𝐶 = 1 + 𝜀𝑒𝑖𝜔𝑡 , 𝜃 = 1 + 𝜀𝑒𝑖𝜔𝑡

𝜕𝑡

𝜌𝐶𝑝 𝜕𝑦�2 − 𝜌𝐶𝑝 𝜕𝑦� + 𝐶𝑠 𝐶𝑝 𝜕𝑦�2 (7)

𝑦 → ∞
∶ 𝑢 → 0, 𝜃 → 0 , 𝐶 → 0.
(16)
concentration equation:

3 Method of solution

𝜕𝐶 = 𝐷 𝜕 𝐶

𝐷𝑚 𝐾𝑟 𝜕2 𝑇�

For 𝜀 ≪ 1, we apply the perturbation scheme

𝜕𝑡

𝜕𝑦�2 + 𝑇

𝜕𝑦�2 (8)

(𝑦, 𝑡) = 𝑓 (𝑦) + 𝜀𝑒𝑖𝜔𝑡 𝑓 (𝑦) + 𝑜(𝜀2 ) (17)

𝑚 𝑓 0 1

where, β is the volumetric co-efficient of expansion for heat
transfer, 𝛽 is the volumetric co-efficient of expansion for the
to equations (13) to (15) where 𝑓 represents 𝑢, 𝜃 and 𝐶.
Comparing the coefficients of various powers of 𝜀 and
fluid, 𝐵0 is the magnetic field,
�𝑡
is the time, 𝑇� is the

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 13

ISSN 2229-5518

neglecting those of second and higher powers of 𝜀, we get
the following equations.

3.1 Zeroth order equations

𝑑𝑦2 − 𝑀𝑢0 = −𝐺𝑟 𝜃0 − 𝐺𝑚 𝐶0 (18)

The visco-elastic effect is exhibited through the non zero values of the non-dimensional parameter K1 . The Newtonian fluid flow mechanism can be illustrated throughout the study by considering K1 =0 and it is worth mentioning that these results show conformity with that of Uwanta et al. [18].

𝑑2 𝜃0 − 𝐾 𝑃 𝜃

= −𝑃 𝐷

𝑑2 𝐶0

(19)
To understand the physics of the problem the first order

𝑑𝑦2

2 𝑟 0

𝑟 𝑢 𝑑𝑦2

velocity 𝑢1 is depicted against y in the figures 1 and 2. The

1 𝑑2 𝐶0

𝑑2 𝜃0

behavior of skin-friction coefficient 𝜎
against M, S , S , D

𝑆𝑐 𝑑𝑦2 + 𝑆𝑟 𝑑 𝑦2 = 0 (20)

3.2 First order equations

0 c r u

and Pr on the plate y=0 is illustrated in the figures 3 to 12.
The numerical calculations are to be carried out for K=.1,

𝜋

𝐾2=.2, 𝜔𝑡 =

, 𝜔 = 1, 𝜀=.001 throughout the discussion.

(1 − 𝑖𝜔𝐾1 )

𝑑2 𝑢1

𝑑𝑦2

− (𝑀 + 𝑖𝜔)𝑢1 = −𝐺𝑟 𝜃1 − 𝐺𝑚 𝐶1 (21)
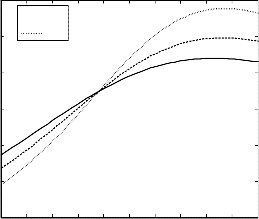
For externally cooled plate (𝐺𝑟 > 0), the first order velocity
profile u1 (figure 1) exhibits an accelerating trend with the

𝑑2 𝜃1 − 𝑃 (𝐾

+ 𝑖𝜔)𝜃
= −𝑃 𝐷

𝑑2 𝐶1

(22)
growing effect of visco-elasticity. It is also observed that the

𝑑𝑦2

𝑟 2

1 𝑟

𝑢 𝑑𝑦2

𝑑2 𝐶1 − 𝑖𝜔𝑆 𝐶

= −𝑆 𝑆 𝑑 𝜃1
(23)
velocity field enhances near the plate y=0 and then

𝑑𝑦2

𝑐 1

𝑟 𝑐 𝑑 𝑦2

diminishes with the increasing values of y.
The modified boundary conditions are
𝑦 = 0 ∶ 𝑢0 = 1, 𝜃0 = 1 , 𝐶0 = 1 , 𝑢1 = 0, 𝜃1 = 1,
𝐶1 = 1.
𝑦 → ∞ ∶ 𝑢0 → 0, 𝜃0 → 0, 𝐶0 → 0 , 𝑢1 → 0,
𝜃1 → 0, 𝐶1 → 0. (24)
Solutions of the equations (18) to (23) are obtained as
follows:

𝑢0 = 𝑏1𝑒−√𝑀𝑦 + 𝑏2 𝑒−𝐷2 𝑦 (25)

𝜃0 = 𝑒−𝐷2 𝑦 (26)

𝐶0 = 𝑒−𝐷2 𝑦 (27)

𝑢1 = 𝑏7𝑒−𝐿𝑦 + 𝑏8𝑒−𝐻1 𝑦 + 𝑏9 𝑒−𝐻2 𝑦 + 𝑏10 𝑒−𝐺1 𝑦 + 𝑏11 𝑒−𝐺2 𝑦 (28)

𝜃1 = 𝑏5𝑒−𝐻1 𝑦 + 𝑏6𝑒−𝐻2 𝑦 (29)

𝐶1 = 𝑏3 𝑒−𝐺1 𝑦 + 𝑏4𝑒−𝐺2 𝑦 (30)

The velocity profile u is given by
𝑢 = 𝑢0 + 𝜀𝑒𝑖𝜔𝑡 𝑢1 (31)
For externally heated plate (𝐺𝑟 < 0), the first order velocity
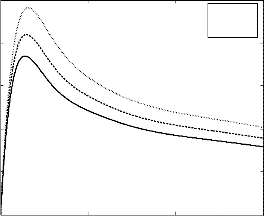
profile u1 (figure 2) reveals a decelerating trend with the
growing effect of visco-elasticity. Also the velocity field
decreases near the plate y=0 and then rises with the increasing values of y.
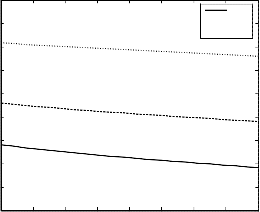
Figure 3 depicts that the skin friction coefficient 𝜎0 against
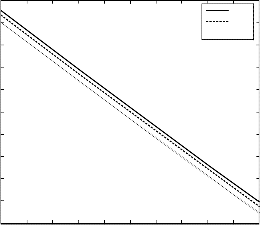
the magnetic parameter M decreases with the growing
effect of the visco-elastic parameter K1 and the magnetic
parameter M as well for externally cooled plate (𝐺𝑟 > 0) .
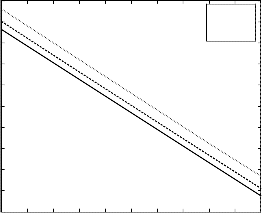
From figure 4, it is observed that the skin friction coefficient
decreases with the enhancement of the magnetic parameter
M but increases with the growth of the visco-elastic
parameter K1 for externally heated plate (𝐺𝑟 < 0).
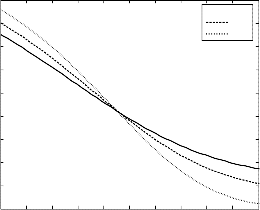
The behavior of the skin friction coefficient against Schmidt
number is illustrated in figures 5 and 6. It is observed from
The non-dimensional skin friction coefficient 𝜎0 on the plate
y=0 is given by
figure 5 that for externally cooled plate (𝐺𝑟
> 0), the skin

𝜎0 = �

𝜕𝑢

− 𝐾1

𝜕2 𝑢 �

={𝑢0 ′ + 𝜀𝑒𝑖𝜔𝑡 (𝑢1 ′ − 𝑖 𝜔𝐾1 𝑢1′)}𝑦=0 (32)
friction coefficient increases up to S c =.85 and then
decreases with the growing effect of the visco-elastic

𝜕𝑦

𝜕𝑡𝜕𝑦 𝑦=0

The non-dimensional rate of heat transfer in terms of
Nusselt number Nu is given by,

𝜕𝑇

parameter K1. It is also found that the skin friction
coefficient decreases with the increasing values of Schmidt
number Sc .

𝑁𝑢 = �
�

𝜕𝑦 𝑦=0

= (𝑇0 ′ + 𝜀𝑒𝑖𝜔𝑡 𝑇1 ′)𝑦=0 (33)
An opposite nature in the behavior of the skin friction
The non-dimensional rate of mass transfer in terms of
Sherwood number 𝑆ℎ is given by

𝜕𝐶

coefficient against Sc is observed from figure 6 for
externally heated plate (𝐺𝑟 < 0).

𝑆ℎ = �
�

𝜕𝑦 𝑦=0

= (𝐶0 ′ + 𝜀𝑒𝑖𝜔𝑡 𝐶1 ′)𝑦=0 (34)
Figure 7 illustrates that the skin friction coefficient against
where dash denotes differentiation w.r.t. y.
The constants are obtained but not given here due to
brevity.

4 Results and discussion

The object of the present paper is to study the effects of visco-elasticity on the free convective MHD flow with heat and mass transfer over a vertical plate in presence of Dufour and Soret effects along with other flow parameters.
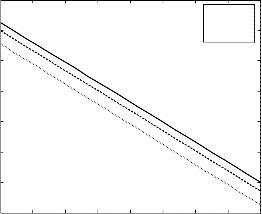
Soret number Sr diminishes with the growing effect of the
visco-elastic parameter K1 and the Soret number Sr as well
for externally cooled plate (𝐺𝑟 > 0).
Figure 8 depicts that the skin friction coefficient against
Soret number Sr enhances with the growing effect of the
visco-elastic parameter K1 for externally heated plate
(𝐺𝑟 < 0) but it decelerates with the rise of Soret number Sr .
Figure 9 shows that the skin friction coefficient against
Dufour number Du diminishes with the growing effect of the visco-elastic parameter K1 and the Dufour number Du
as well for externally cooled plate (𝐺𝑟 > 0).

International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 14

ISSN 2229-5518

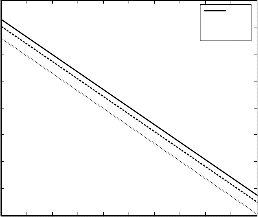
Figure 10 exhibits that the skin friction coefficient against Dufour number Du accelerates with the growing effect of the visco-elastic parameter K1 for externally heated plate
(𝐺𝑟 < 0) but it decelerates with the rise of Dufour number
Du .
It is observed from figure 11 that the skin friction coefficient
against Prandtl number Pr decelerates with the rising effect
of the visco-elastic parameter K1 and the Prandtl number Pr
as well for externally cooled plate (𝐺𝑟 > 0).
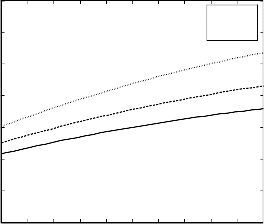
Figure 12 reveals an accelerating trend of the skin friction
coefficient against Prandtl number Pr with the growth of
the visco-elastic parameter K1 and Prandtl number Pr as
well for externally heated plate (𝐺𝑟 < 0).

-2

-4

-6

-8

-10

-12

-14

-16

x 10

K1 .1

K1 .2

The temperature and concentration fields are not affected
by the growth of visco-elastic parameter.

0 5 10 15 y

Fig 2: First order velocity profile u1 against y for M=1, D u =.1, P r =.2, Gr =-3, G m =3, S c =1, Sr =.1

7.12

7.11

7.1

x 10

K =0

K =.1

K =.2

7.09

2.5

x 10

K =0

K1 .1

K1 .2

7.08

7.07

7.06

7.05

7.04

1.5

7.03

0.5

7.02

0.4 0.401 0.402 0.403 0.404 0.405 0.406 0.407 0.408 0.409

Figure 3: Skin friction coefficient σ 0 against M for D u =.1, P r =.2, G r =3, G m =3, Sc =1, S r =.1

0 5 10 15

-6.3

-6.31

-6.32

x 10

K =0

K =.1

K =.2

Fig 1: First order velocity profile u1 against y for M=1, D u =.1, P r =.2, G r = 3, G m = 3, Sc =1, Sr =.1

-6.33

-6.34

-6.35

-6.36

-6.37

-6.38

-6.39

-6.4

0.4 0.401 0.402 0.403 0.404 0.405 0.406 0.407 0.408 0.409

Figure 4: Skin friction coefficient σ 0 against M for D u =.1, P r =.2, G r =-3, G m =3, Sc =1, S r =.1

International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 15

ISSN 2229-5518

4.258

4.2575

4.257

x 10

K =0

K =.1

K =.2

-9.9946

-9.9948

-9.995

x 10

K =.1

=.2

4.2565

-9.9952

4.256

-9.9954

4.2555

4.255

4.2545

-9.9956

-9.9958

-9.996

4.254

-9.9962

4.2535

0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4

Figure 5: Skin friction coefficient σ 0 against S c for D u =.1, M=1, Pr =.2, G r =3, G m =3, S r =.1

-9.9964

0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

Figure 8: Skin friction coefficient σ 0 against Sr for D u =.1, M=1, P r =.2, G r =-3, G m =3, S c =1

-9.994

-9.995

x 10

K =0

K =.1

K1 .2

4.2555

4.255

x 10

K =0

K =.1

K =.2

-9.996

4.2545

-9.997

-9.998

4.254

4.2535

4.253

-9.999

4.2525

-10

0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4

Figure 6: Skin friction coefficient σ 0 against Sc for D u =.1, M=1, Pr =.2, G r =-3, G m =3, S r =.1

4.252

0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

Figure 9: Skin friction coefficient σ 0 against D u for Sr =.1, M=1, P r =.2, Gr =3, G m =3, S c =1

4.2555

4.255

4.2545

x 10

K =0

K =.1

K =.2

-9.9946

-9.9948

-9.995

-9.9952

x 10

K =0

K =.1

=.2

4.254

-9.9954

4.2535

4.253

-9.9956

-9.9958

-9.996

4.2525

-9.9962

4.252

0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

Figure 7: Skin friction coefficient σ 0 against Sr for D u =.1, M=1, P r =.2, Gr =3, G m =3, S c =1

-9.9964

0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

Figure 10: Skin friction coefficient σ0 against D u for S r =.1, M=1, Pr =.2,

International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 16

ISSN 2229-5518

x 10

4.2555

4.255

K =.1

K =.2

 The temperature and concentration fields are not affected by the growth of visco-elasticity.

REFERENCES

4.2545

4.254

4.2535 4.253

4.2525

4.252

4.2515

0.2 0.2002 0.2004 0.2006 0.2008 0.201 0.2012 0.2014 0.2016 0.2018 0.202

Figure 11: Skin friction coefficient σ 0 against P r for D u =.1, M=1, G r =3, G m =3, Sr =.1, Sc =1.

x 10

K =0

K1 .1

[1] G.G. Stokes, “On the effects of internal friction of fluids

on the motion of pendulum,” Thammasat Int. J. of Sci. and Tech., vol. 9, pp. 8-106, 1856.

[2] A. Raptis and N.G. Kafousias, “MHD free convection

flow and mass transfer through porous medium bounded by an infinite vertical porous plate with constant heat flux,” Cambridge J. Phys., vol. 60, pp. 1725-1729, 1982.

[3] B. K. Jha and A.K. Singh, “Soret Effect on free convection

and mass transfer flow in the Stokes problem for an infinite vertical plate,” Astrophys. and Space Sci., vol. 173, pp. 251-255,

1990.

[4] Z. Dursunkaya and W.M. Worek, “Diffusion thermo and

thermal-diffusion effects in transient and steady natural convection from vertical surface,” Int. J. Heat and Mass Trans., vol.

35, no. 8, pp. 2060-2065, 1992.

[5] N.G. Kafoussias and E.M. Williams, “Thermal-diffusion

and diffusion-thermo effects on mixed free forced convective and mass transfer boundary layer flow with temperature dependent,” Int. J. of Engg. Sci., vol. 33, no. 9, pp. 1369-1384, 1995.

-9.992

-9.993

-9.994

-9.995

-9.996

-9.997

-9.998

=.2

[6] M. Anghel, H.S.Takhar and I. Pop, “Dufour and Soret

effects on free convection boundary layer over a vertical surface embedded in a porous medium,” J. of Heat and Mass Trans., vol.

43, pp. 1265-1274, 2000.

[7] E. M. Aboeldahab and E. M. Elbarbary, “Hall Current

Effect on Magnetohydrodynamic free convection flow past a semi infinite vertical plate with mass transfer,” Int. J. of Engg. Sci., vol.

39, pp. 1641-1652, 2001.

[8] A. A. Megahead, S. R. Komy and A. A. Afify, “Similarity

Analysis in MHD effects on free convection flow and mass transfer past a semi-infinite vertical plate,” Int. J. Non-linear media, vol.

38, pp. 513-520, 2003.

[9] A. Postelincus, “Influence of a magnetic field on heat and

mass transfer by a natural convection from vertical surfaces in

0.2 0.22 0.24 0.26 0.28 0.3 0.32 0.34 0.36 0.38 0.4

Figure 12: Skin friction coefficient σ 0 against P r for D u =.1, M=1, G r =-3, G m =3, Sr =.1, Sc =1.

5 Conclusion

An analysis of free convective MHD flow of a visco-elastic fluid with heat and mass transfer over a vertical plate in presence of Dufour and Soret effects is presented.
From this study, we make the following conclusions:

 The velocity field is considerably affected by the visco-

elastic parameter along with other flow parameters at all points of the fluid flow region.

 The first order velocity profile exhibits an accelerating trend with the growing effect of visco-elasticity for externally cooled plate but an opposite trend is observed for externally heated plate.

 The skin friction coefficient on the plate is significantly

affected by the visco-elastic parameter along with other flow parameters.

porous media considering Soret and Dufour effects,” Int. J. Heat and Mass Trans., vol. 47, no. 6-7, pp. 1467-1472, 2004.

[10] M. A. Sedeek, “Thermal-diffusion and diffusion-thermo

effects on mixed free- forced convective flow and mass transfer over accelerating surface with a heat source in the presence of suction and blowing in the case of variable viscosity, Acta Mechanica, vol. 172, pp. 83-94, 2004.

[11] C. H. Chen, “Heat and Mass transfer in MHD flow by

natural convection from a permeable, inclined surface with variable wall temperature and convection,” Acta Mechanica, vol.

22, pp. 219-235, 2004.

[12] M. S. Alam and M. M. Rahman, “Dufour and Soret

effects on MHD free convective heat and mass transfer flow past a vertical flat plate embedded in porous medium,” J. Naval Arch. and Marine Engg., vol. 2, no. 1, pp. 55-65, 2005.

[13] I. Nazmul and A. Mahmud, “Dufour and Soret effects

on steady MHD free convection and mass transfer fluid flow through a porous medium in a rotating system,” J. of Naval Arch. and Marine Engg., vol. 4, no. 1, pp. 43-55, 2007.

[14]F. S. Ibrahim, A. M. Elaiw and A. A. Bakr, “Effects of the

chemical reactions and radiations absorption on the unsteady MHD free convection flow past a semi-infinite vertical permeable moving plate with heat source and suction,” Cambridge J. Phys., vol. 78, pp. 255-270, 2008.

International Journal of Scientific & Engineering Research, Volume 4, Issue 7, July-2013 17

ISSN 2229-5518

[15]R. N. Ananda, V. K. Varma and M. C. Raju, “Thermal

diffusion and chemical effects with simultaneous thermal and mass diffusion in MHD mixed convection flow with ohmic heating,” J. of Naval Arch. and Marine Engg., vol. 6, pp. 84-93,

2009.

[16]O. A. Beg and S. K. Ghosh, “Analytical study of magnetohydrodynamic radiation convection with surface temperature oscillation and secondary flow effects,” Int. J. of Appl. Math. and Mech., vol. 6, no. 6, pp.1-22, 2010.

[17] I. J. Uwanta , B. Y. Isah and M.O. Ibrahim, “Radiative convection flow with chemical reaction,” Int. J. of Computer applications, vol.

36, no. 2, pp. 25-32, 2011.

[18]I. J. Uwanta, K. K. Asogwa and U. A. Ali, “MHD fluid flow over a vertical plate with Dafour and Soret effects,” Int. J. of Computer Applications, vol. 45, no.2, pp. 8-16, 2008.

[19]M. A. Mansour, N. F. El-Anssary, A. M. Aly, “Effect of chemical reaction and thermal stratification on MHD free convective heat and mass transfer over a vertical stretching surface embedded in a porous media considering Soret and Dufour number,” Chem. Engg. J., vol. 145, pp. 340 – 345, 2008.

[20]P. O. Oladapo, “Dufour and Soret effects of a transient free

convective flow with radiative heat transfer past a flat plate moving through a binary mixture,” Pacific J. of Sci. and Tech., vol.11, no.1, pp. 163-172, 2010.

[21] K. Walters, “The motion of an elastico-viscous liquid contained

• Rita Choudhury is HOD and professor, Department of

Mathematics, Gauhati University, Guwahati-781 014, Assam, India

Email: rchoudhury66@yahoo.in

• Sajal Kumar Das is Associate Professor, Department of Mathematics, Bajali College, Pathsala, Barpeta, Assam, India. Email: sajall2003@yahoo.co.in

between co-axial cylinders (II),” Quart. J. Mech. Appl. Math., vol.

13, pp. 444-461, 1960.

[22] K. Walters, “The solution of flow problems in the case of materials with memories,” J. Mecanique, vol.1, pp. 473-478, 1962.