International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1159

ISSN 2229-5518

Two-Point Resolution capabilities for an optical system with parabolic filters as functions of the degree of coherence of illumination Part-II

P. Thirupathi* , T.RamakrishnaGoud**

Abstract-Definition and determination of an image quality criterion has long been and still is a major one in the field of image evaluation and assessment. In this paper the two-point resolution capabilities have been investigated for an optical system with parabolic filters. The Rayleigh and the Sparrow resolution limits are computed and studied as functions of the incoherent, coherent and partially coherent illumination and the ratio of the normalized intensity of the two point objects. The ‘coded imaging (CI)’ technique a two step process has been used to overcome the limitations of the conventional methods involving the cases of sources of short wavelength radiations, due to their high penetrating power and rectilinear propagation during the imaging. Any criterion of resolution is not a law of physics and the resolving power depends on a three-fold combination of energy of the source, instrument and its energy distribution capabilities and receiver and its sensitivity characteristics, irrespective of the arbitrariness of these criteria, they still serve the purpose of comparison of the performance of the imaging systems and yield useful rules of thumb for engineering practice. The results of the investigations carried out on the problem of two–point resolution under various imaging situations have been presented and discussed. Two object points of equal as

wγell as unequal intensities ( ) for different object separations (Z0β) have been considered for various values of the coherence parameter (

) of illumination for a fixed value of the apodisation parameter ( )

Key words: Two-Point Resolution, Image Intensity Distribution, Fourier Optics, Coherence Parameter, Rayleigh Criterion, Sparrow Criterion

* Department of Mathematics, University College of Engineering, Osmania University, Hyderabad-500 007, INDIA

** Department of Mathematics, University College of Science Saifabad,

Osmania University, Hyderabad-500 007, INDI

1. Introduction

The two-point resolution capabilities have been investigated for an optical system with parabolic filters. The Rayleigh and the Sparrow resolution limits are computed and studied as functions of the degree of coherence of illumination, (Incoherent, coherent and partially coherent) and the ratio of the intensity of the two point objects. The problem of the definition and determination of an image quality criterion has long been and still is a major one in the field of image evaluation and assessment.
The intensity distribution in the image was obtained such that it satisfied the requirement of the criteria chosen. The limiting separation thus determined gave the imaging system’s response in terms of two-point resolution. Coded Imaging (CI) techniques have been employed in determining the source location and the source distribution as it accounts for the sources of short wave length radiations such as X- rays, gamma rays or sub-atomic particles, thus overcoming the shortcomings in the usage of the conventional methods of ray bending i.e., reflection, refraction and diffraction, which cannot be used for imaging due to their high penetrating power and
rectilinear propagation. According to them “CI”, when reduced to the basics, is a two step process.
In the first step, the source information is recorded or encoded by geometrical shadow casting through a coded aperture (no ray bending is involved). In the second step, the image is matched to the coded aperture design. Though the two-point resolution is one of the simplest criterion to assess the performance of optical imaging systems, it has its inherent complexity owing to the fact that the limit of resolution is sensitive to a large number of factors via., nature of the optical system, nature of illumination, object point separation, intensity ratio of the object points degree of coherence, resolution criterion used, etc. The methodology employed in this paper has flexibility in the exact quantitative definition of the limiting resolving power achievable. It may be noted that the resolving power of an imaging system as determined by the Rayleigh criterion which is not the property of the system alone but also of the pair of objects and the coherence condition of illumination has its advantages over the optical transfer function which involves non-linearities for optical systems operating in partially coherent illumination, if the

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1160

ISSN 2229-5518

detection step is also included in the imaging system. Due to the non-linearity associated with the partially coherent imaging systems, the systems become object-dependent and cannot be completely characterized by a system transfer function as in the linear case.

2. Various Resolution Criteria

As the subject of two-point resolution is sensitive to a wide variety of factors, a criterion of resolution is required in order to determine the limit of resolution. Several criteria have been proposed from time to time. It should be mentioned that all criteria of resolution are arbitrary and as BARAKAT [1] has mentioned, any criterion of resolution is not a law of physics. It may be pointed out that none of these criteria either determines or sets an absolute limit on the limit of resolution. Therefore, it is meaningless to talk about the absolute resolving- power of an imaging system. The resolving-power, as RONCHI [2] opined, depends on a three-fold combination of

• The source and its energy,

• The instrument and its energy distribution

capacities and

• The receiver and its sensitivity characteristics

These criteria serve the purpose of comparison of the performances of various imaging systems. They “yield useful rules of thumb for engineering practice”. The Rayleigh and Sparrow criteria of resolution used in the present study are explained in more details. The subject of two-point resolution starts with the celebrated Rayleigh criterion. Lord RAYLEIGH [3] developed the first resolution criterion, which now bears his name. Rayleigh recognized the arbitrariness of the criterion. In his own words, “This rule is convenient on account of its simplicity and it is sufficiently accurate in view of the necessary uncertainty as to what is meant by resolution”. Rayleigh criterion, through arbitrary, has the virtue of being particularly uncomplicated.
SPARROW gave the alternate criterion which he called “undulation condition”. ASAKURA [4] recognizing that the case of object points having equal intensity is rare in actual imaging situations, introduced the “modified Sparrow criterion” to suit actual imaging situations and studied the problem of two-point resolution of unequally bright points under partially coherent illumination. BHATNAGAR, SIROHI and SHARMA [5] proposed a criterion for the case of unequally bright points.
Rayleigh and the Sparrow criteria have been the most extensively used criteria in the field of image science. It may be mentioned that these criteria are based, directly or indirectly, on the (PSF). The reasons for choosing these two criteria for the present dissertation are given below.

• In the field of image science, both the Rayleigh

and Sparrow criteria have been and are still being used extensively in the assessment performance of optical imaging systems.

• Several workers have modified these criteria to

suit various imaging situations for the purpose of comparing and assessing the performance of optical systems.

• As the Rayleigh criterion has limited

applicability, we have chosen the Sparrow criterion also. The Sparrow criterion is sensitive to various parameters such as intensity ratio of object points, non-uniform transmission of the aperture, degree of coherence of illumination of the object points. The Sparrow criterion is amenable to quantitative calculations

• It has been empirically found that the effects of

noise limitations on the two-point resolution correlate well with these two criteria.
A vast amount of literature has been reported by several authors on this subject. The papers of CESINI et. al. [6], BARAKAT [7], and MILLS and THOMPSON [8] provide a very good review of the studies on this subject.
The survey of the literature reveals that both the Rayleigh and Sparrow criteria were modified to suit various imaging situations, CHATURVEDI and SODHA [9], ASAKURA [4], JAISWAL and BHOGRA [10], BHATNAGAR, SIROHI and SHARMA [5], etc. CARSWELL and RICHARD [11] suggested a criterion for coherent system as an extension of Rayleigh criterion. The two-point resolution studies for one- dimensional systems have been made by ROJAK [12] for intermediate states of coherence NYYSSONEN and THOMPSON [13] have plotted and studied the actual intensity distribution in the image for the coherent and actual intensity distribution in the image for the coherent and incoherent extremes. GRIMES and THOMPSON [14] discussed the two- point resolution with partially coherent light for equally bright object points. They have studied the relation between the measurable and the real separations of the two object points and also verified it experimentally. GUPTA, SIROHI and NAYYAR [15] used the Sparrow criterion and derived an expression to obtain the limit of resolution or an annular aperture in partially coherent light. They have also studied the variation of the critical resolution for various obscuration ratios and found a near linear relation. A few studies have also been reported on the problem of two- point resolution in microscopes. BASURAY [16] has studied the two-point resolution of phase objects in partially coherent light in ordinary microscopes. BHATNAGAR and SIROHI [17] have studied the effect of a centrally obstructed condenser on resolution of a microscope. MEHTA [18] employed Sparrow criterion and investigated the dependence of the critical resolution of coherent properties of the point’s sources taking into account non-uniformity of illumination. He found that the non- uniform illumination has increased the just resolvable separation. MEHTA, VIRDI and NAYYAR [19] studied the two-point resolution by a circular aperture employing non- uniform and non-symmetric illumination. SODHA and AGARWAL [20] discussed the dependence of the limit of resolution of telescopes on various factors like the intensity

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1161

ISSN 2229-5518

ratio, background intensity and the ratio of the minimum to the lower maximum of the resultant intensity pattern of the two objects. BHATNAGAR, SIROHI and SHARMA [5] made use of the modified Rayleigh criterion and investigated the dependence of the limit of resolution, on the intensity ratio and the background intensity in partially coherent light.
The literature is rich in the studies on the effect of apodisation on the two-point Resolution of imaging systems. BARAKAT and LEVIN [21] used apodization to increase the two-point resolution in terms of the Sparrow criterion, for both coherent and incoherent cases. ASAKURA and UENO [48] also employed apodisation to increase two-point resolution and obtained the required pupil function by solving the homogeneous Freehold integral equations. SHANKARAIAH et.al. [23] used Gaussian apodisation and studied the resolution of two unequally bright points in partially coherent illumination. NAYYAR and VERMA [24] have discussed the partially coherent two-point resolution of a Gaussian aperture making use of several resolution criteria. MAGIERA and MAGIERA [25] study the partially coherent two-point resolution by Walsh-type apertures using the Sparrow criterion.
GRUBER and THOMPSON [26] have discussed the effect of apodisation in coherent imaging systems. SURENDAR et al [27] have used Lanczos’ filters and studied the resolution of unequally bright points in partially coherent illumination. THOMPSON [28] has investigated the diffraction by annular apertures with semi-transparent central regions that add a uniform phase and found an improved two-point resolution. NAYYAR [29] has discussed two-point resolution employing both the Rayleigh and Sparrow criteria for the
semi-transparent π -phase annular apertures and for the
annulus in partially coherent illumination. NAYYAR and
VERMA [24] have investigated the effect of non-uniform and non-symmetric illumination on the two-point resolution of a
microscope using a semi-transparent π -phase annular
aperture.
There have been a few studies NAYYAR [29] Mc KECHNIE [30] on the two-point resolution for two anti – phase coherent point objects with a theoretical prediction of an
will behave more like a coherent situation. The influence of partially coherent illumination and spherical aberration on microscopic resolution has been studied by SOM [31]. The difference between the actual and measured separation (peak- to peak distance in the image plane) of the two object points has been called “mensuration error” MILLS and THOMPSON [8].

3. The Resolution Criterion

A) The Rayleigh Criterion

It states that “the two point sources are just resolved if the maximum of one irradiance pattern coincides with the first minimum of the other”. This means that two closely spaced points can be considered as just resolved if we are able to distinguish the resultant PSF in the image as being due to two objects instead of one. It may be pointed out the Rayleigh proposed his criterion to be used for line spectra in Spectroscopy. But it can be equally applied for images of point objects as well. In its original form, the Rayleigh criterion is applicable to two equally bright points under incoherent illumination. The Rayleigh criterion implies a pronounced central dip (minimum) in the resultant image intensity distribution curve of the equally bright and incoherent object points. This dip or the ‘saddle point’ is midway between the two PSF peaks. For circular apertures, the dip-point intensity is
73.5% of the maximum intensity. This implies a drop of 36.5%
in intensity.
The coherent Rayleigh limit for two dimensional
systems is 5,146 dimensionless diffraction units for point objects of equal intensity. In the resultant image intensity distribution curve a smaller drop in intensity is associated with a smaller limit of resolution. Several researchers, to suit various imaging situations, modified the Rayleigh criterion. To suit the case of object points of unequal intensities TOLANSKY [32], CHATURVEDI and SODHA [33] modified the Raleigh criterion. In the redefined Rayleigh criterion, the two objects points are said to be just resolved, if the contrast between the
infinite degree of resolution which has been exploited in holographic spectroscopy. MILLS and THOMPSON [8] have
lower intensity peak

I LP

and the dip (saddle point) point of
combined apodisation and aberration and examined the Sparrow limit for spherical aberration, coma and defocus, both with and without apodisation. They employed Gaussian
minimum intensity Dip is given by,

I Dip = 0.735

LLP − I Dip

= 0.265

apodisers Mc KECHNIE [30].In this case, the value of γ is
neither 0 (incoherent Illumination) nor 1 (Perfectly Coherent

……………(2)
or LP
Illumination), as γ can assume any value in the range of 0 < γ <

1 the equation (3) to be discussed in the later sections will

remain unchanged.
BHATNAGAR, SIROHI and SHARMA [5] have employed the above modified Rayleigh criterion for case of unequally bright object points. The corresponding value for

I ( Z ) = G ( Z − B )2 + α G ( Z + B )2 + 2

……………(1)

α .γ ( Z0

) G ( Z − B )tGwo( Zlin+es Bis)0 .19.

B) The Sparrow Criterion

Obviously, the values of γ close to 0 will behave more like an incoherent situation, whereas, the values of γ close to 1
Sparrow recognized the limitations and the arbitrariness involved in the Rayleigh criterion, (Viz. for

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1162

ISSN 2229-5518

intensity spread functions having non-zero minima or coherent systems or for unequally bright point objects) and observed that “as originality proposed, the Rayleigh criterion was not intended as a measure of the actual limit of resolution, but rather as an index of the relative merit of different instruments”. Sparrow proposed an alternate criterion of resolution, which he is called “the undulation condition. According to this criterion, two object points can just be resolved when the second derivative of the total intensity distribution in the diffraction image of the two object points, vanishes at a point midway between the respective Gaussian image points. When this condition is satisfied, the distance between the two object points gives the Sparrow Limit of resolution(SL),. According to this criterion, two object points are said to be just resolved if in the resultant intensity distribution curve, the central dip just vanishes. The separation between the object points under these conditions gives the Sparrow Limit (SL).
The Sparrow criterion was applied to incoherent illumination; the immediate generalization to coherent illumination is due to LUNEBERG[34]. In the holographic image formation under partially coherent illumination and in the defocused image of two points in partially coherent or coherent illumination, the object points are of unequal intensities. Realizing this aspect, ASAKURA [4] introduced the “modified Sparrow criterion” to suit the situation of actual object points which are unequally bright. This modified Sparrow criterion is relevant in such practical imaging systems.
The “modified Sparrow criterion” states that, “the
resolution is retained, when the second derivative of the image intensity distribution vanishes at a certain point (Z= Z0 ’) between two Gaussian image points, with the condition that this point Z0 ’ should be a solution for the first derivative of the image intensity distribution becoming zero”. The modified Sparrow criterion can be mathematically written as,

∂2 I ( z )

Two objects points of equal as well as unequal intensities have been considered along with the effects of degree of coherence and the intensity ratio of object points on image intensity distribution.
Primarily it can be concluded from the distribution
curves that the actual separation between two object points assumed to be of equal brightness, has been larger than the critical limit (SL), the dip in the resultant intensity distribution curve is at the midpoint between the two Gaussian image points.
As the actual separation between the object points is decreased, the dip-point decreases in its upward concavity and it just vanishes at a particular separation of the two object points.
The separation between the object points under this

condition of the vanishing dip gives the Sparrow limit of resolution Z 0 ’. The Rayleigh criterion implies a finite contrast in the image while Sparrow criterion leads to the limiting case of vanishingly small contrast “In its original context.

When the two object points are of equal intensities
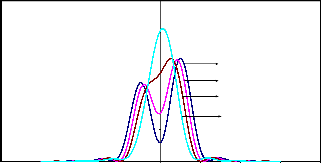
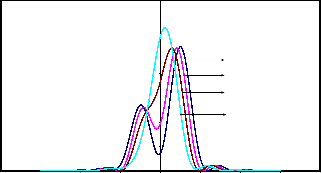
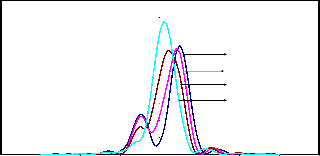
and very well separated, in the resultant intensity distribution curve, there will be a very well pronounced dip point, which is located at the centre between the Gaussian image points. When the two object points are of unequal intensities, it is noticed that the dip point in the resultant intensity distribution curve is not located midway between the two Gaussian image points.
It is also observed that as the difference between the
intensities of the object points increases, the dip point is found to shift towards lower peak in the intensity distribution curve.
As the two object points come closer, the dip
disappears at a certain separation. This vanishing dip-point becomes a point of inflection which is no longer a minimum or maximum point.
At this point, both the first and the second derivatives of the resultant intensity distribution become zero, thus satisfying the condition of the critical limit (SL).
When , it implies that there is only one point

∂Z 2

and

∂2 I ( z )

∂Z 2

atz = z0′ = 0

……………(3)
object in the object plane, by shifting the only point object in the transverse plane, we could verify the shift theorem of Fourier transforms. Further, as far as the two-point resolution in incoherent illumination is concerned, we find that the limit of resolution is 3.84 diffraction units which agrees perfectly well with the Rayleigh criterion of resolution.
When there are two-point objects (≠) the
lateral shift in the position of the resultant intensity
(35)

4. Formulation of the problem

We discussed about formulation in previous paper

5. Results an Discussions

5.1 Two Point Resolution (TPR)

The results of the investigations carried out on the
distributions are different from the corresponding values of shift for a particular value of the lateral shift of the positions of the two-point objects in the object plane. It means that the shifting theory of Fourier transform is not valid. This can be accounted for by remembering that an optical system operating in partially coherent illumination is a non-linear system. Thus, the theorems of Fourier transform which hold good for in linear systems only. Further, the lateral shift in the position of the resultant intensity distributions go on
problem of two–point resolution under various imaging situations have been presented and discussed.
diminishing with increasing values of 

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1163

ISSN 2229-5518

5.2 TPR In Incoherent Illumination( γ = 0)

2.5

In figures 5.2 (a) to 5.2 (d) we have presented the resultant intensity distributions in the images of two point
objects of unequal intensities α =0, 0.25, 0.50&0.75 for different
objects separations Z 0 =2.0, 3.0, 4.0 & 5.0. Identically, the effects of β , the apodization parameter on the intensity distributions
are, by now, well understood from the discussions made in the

I(z)

1.5

z0=5 z0=4

previous two chapters of the present dissertations. That is why we have kept the value β fixed ( β = 1.0 ) in all the cases.

1 z0=3

z0=2

Further, α = 0
signifies that there is only one point object in

0.5

-20 -15 -10 -5 0 5 10 15 20

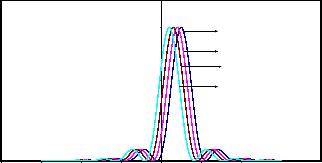
the object plane. It is observed from the figure 5.2 (a) , that
there are four single peaks shifted from the I(z) axis corresponding to four different values of the object separations

z

Fig.5.2 (d) :Resultant Intensity Distributions in Incoherent illumination (g=0) for two point objects (a=0.75)

given by

z0 = 2.0, 3.0, 4.0 & 5.0 .As each individual curve

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

0.3

0.25

z0=5

0.2 z0=4 z0=3

represents the point–spread function for an amount of shift indicated by the value of z0 . This result obviously serves as an example of the shift-theorem of Fourier transforms. Considering the figures 5.2 (b), 5.2(c) & 5.2(d), it is evident

I(z)

0.15

z0=2

from the figures that for the values of

z0 chosen, the two

0.1

object points are well resolved as the two peaks can be seen
distinctly even for z0

0.05

-20 -15 -10 -5 0 5 10 15 20

z

Fig.5.2 (a) : Intensity Distributions in Incoherent illumination (g=0) for a single point object (a=0)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

1.4

1.2

5.3 TPR in Partially Coherent Illumination ( γ =0.5)

z0=5

I(z)

0.8

0.6

z0=4 z0=3

0.9

0.8

0.4

z0=2

0.7

0.6

z0=5

0.2

-20 -15 -10 -5 0 5 10 15 20

z

Fig.5.2 (c) :Resultant Intensity Distributions in Incoherent illumination (g=0) for two point objects (a=0.50)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

I(z)

0.5

0.4

0.3

0.2

z0=4 z0=3

z0=2

0.7

0.1

0.6

0.5

z0=5

-20 -15 -10 -5 0 5 10 15 20

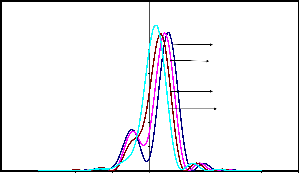
Fig.5.3 (b) :Resultant Intensity Distributions in partially z oherent illumination (g=0.5) for two point objects (a=0.25)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

z0=4

0.3

0.4

I(z)

0.3

z0=3

0.25

z0=5

0.2

z0=2

0.2

z0=4

z0=3

0.1

I(z)

0.15

z0=2

-20 -15 -10 -5 0 5 10 15 20

z

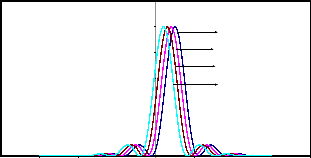
Fig.5.2 (b) : Resultant Intensity Distributions in Incoherent illumination (g=0) for two point objects (a=0.25)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

0.1

0.05

-20 -15 -10 -5 0 5 10 15 20

z

Fig.5.3 (a) : Intensity Distributions in partially coherent illumination (g=0.5) for a single point object (a=0)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1164

ISSN 2229-5518

1.8

5.4 TPR in Coherent Illumination ( γ =1):

1.6

1.4

0.3

I(z)

1.2

0.8

z0=5 z0=4

z0=3

0.25

0.2

z0=5 z0=4

z0=3

0.6

z0=2

I(z)

0.15

z0=2

0.4

0.2

0.1

-20 -15 -10 -5 0 5 10 15 20

z

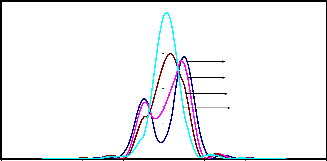
Fig.5.3 (c) :Resultant Intensity Distributions in partially coherent illumination (g=0.5) for two point objects (a=0.50)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

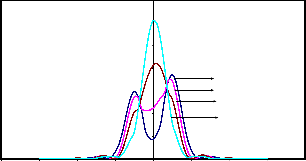
3.5

0.05

-20 -15 -10 -5 0 5 10 15 20

Fig.5.4(a) : Intensity Distributions in coherent illumination (g=1) for a single point object (a=0)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

2.5

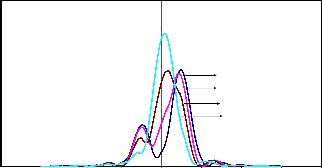
1.2

I(z)

z0=5

1.5

z0=4

z0=3

0.8

0.5

z0=2

I(z)

0.6

z0=5 z0=4

-20 -15 -10 -5 0 5 10 15 20

z

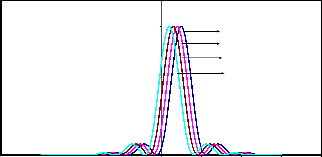
Fig.5.3 (d) :Resultant Intensity Distributions in partially coherent illumination (g=0.5) for two point objects (a=0.75)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

0.4

0.2

z0=3 z0=2

In the figures 5.3 (a) to 5.3(d) we have presented the intensity distributions in partially coherent illumination for a single point object ( α = 0 ) shifted by z0 = 2.0, 3.0, 4.0 & 5.0 on either side of I (z) axis for β = 1.0 . It is observed from the figures that the lateral shift in the position of the PSF for a single point objects ( α = 0 ).

-20 -15 -10 -5 0 5 10 15 20

z

Fig.5.4(b) :Resultant Intensity Distributions in coherent illumination (g=1) for two point objects (a=0.25)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

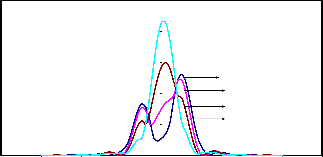
2.5

This means, irrespective of the value of

z0 , the linear shifting-

1.5

property of Fourier transforms is not violated even in partially coherent illumination. However, when there are two point-

I(z)

z0=5

1 z0=4 z0=3

objects (

α ≠ 0 ), the lateral shift in the position of the

0.5

z0=2

resultant intensity distributions are different from the
corresponding values of the shift for a particular value of

z0 .

-20 -15 -10 -5 0 5 10 15 20

Another interesting point to be observed is that this lateral shift in the positions of the resultant intensity distributions
goes on diminishing with increasing values of α . Further, for
well resolved curves, the two unequal peaks corresponding to

z

Fig.5.4(c) :Resultant Intensity Distributions in coherent illumination (g=1) for two point objects (a=0.50)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

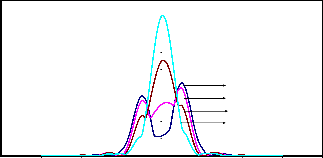
4.5

3.5

the two unequal intensity object-points (

α ≠ 0 ) for each 3

value of

z0 . However, with increasing values of

z0 , the

I(z)

2.5

z0=5

individual peak intensity values go on increasing maintaining,
of course the same intensity ratio as indicated by the value of

α .

1.5

z0=4 z0=3

z0=2

0.5

-20 -15 -10 -5 0 5 10 15 20

z

Fig.5.4(d) :Resultant Intensity Distributions in coherent illumination (g=1) for two point objects (a=0.75)

shifted by z0=2,3,4 & 5 on the either side of the I(z) axes ; b =1.0

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1165

ISSN 2229-5518

In the figures 5.4 (a) to 5.4(d), we have presented the curves for the resultant intensity distributions in the images of two point-objects in coherent illumination ( γ =1). The
discussions made in the previous section for well-resolved
[18] MEHTA, B.L., Appl. Opt., vol.13, 1974.
[19] MEHTA, B.L., VIRDI, S.P.S. and NAYYAR, V.P., Atti. Fond.G. Ronchi, vol.26,1971.
[20] SODHA, M.S. and AGARWAL, A . K., Optik,
object-points for all values of α and

z0 also hold well in

vol.24, 1967.
coherent illumination also, the only difference is in the
absolute value of intensities in all these cases.

6. References

[1] BARAKAT, R., opt. Acta., vol.17, 1969.
[2] RONCHI, V., et.al., Atti. Fond. G. Ranchi., vol.35,
1980.
[3] LORD. RAYLEIGH, Collected papers (Cambridge
Univ. Press, Cambridge), Vol.3, 1902.
[4] ASAKURA,T., Nouv, Rev.opt., vol.5, 1974
[5] BHATNAGAR, G.S., SIROHI, R.S. and SHARMA, S.K., opt. commun., vol.3, 1971.
[6] CESNI, G., et.al., J. optics (paris), vol.10, 1979. [7] BARAKAT, R., J. opt. Soc. Am., vol.52, 1962.
[8] MILLS, J.P. and THOMPSON, B.J., J. Opt.Soc. Am.A., vol. 3, 1986.
[9] CHATURVEDI, K.C. and SODHA, M.S., Indian J. Phys., vol.30, 1956.
[10] JAISWAL, A.K. and BHOGRA, R.K., optica. Acta.,
vol.21, 1974.
[11] CARSWELL, A.I. and RICHARD, C., Appl. Opt., vol.4, 1965.
[12] ROJAK, F., M.S. THESIS, “Two point Resolution with partially coherent Light”, Lowel
Technological Institute, Lowell, mass., 1961.
[13] NYYSSONEN, D. and THOMPSON, B.J., J. opt. Soc. Am., vol.57, 1967.
[14] GRIMES, D.N. and THOMPSON, B.J., J. opt. soc.
Am. vol. 57, 1967.
[15] GUPTA, B.N., SIROHI, R.S. and NAYYAR, V.P., Phys.Letters.,vol.33A,1970.
[16] BASURAY, A., J. opt. India, vol.1, 1972.
[17] BHATNAGAR, G.S. and SIROHI. R.S., optica. Acta., vol.18, 1971.
[21] BARAKAT, R. and LEVIN, E., J. opt. Soc. Am., vol.
53, 1963.
[22] ASAKURA and UENO [48].
[23] SHANKARAIAH, M., et.al., Atti. Fond. G. Ronchi., vol.37, 1982.
[24] NAYYAR, V.P. and VERMA, N.K., Appl. Opt., vol.17,
1978.
[25] MAGIERA, A. and MAGIERA, L.Optica.Applicata., vol.14, 1984.
[26] GRUBER, L.S. and THOMPSON, B.G., opt. Eng.,
vol.13, 1974.
[27] SURENDAR, K., et.al., opt. India, vol.22, 1993.
[28] THOMPSON, B.J., “Image assessment and
Specification” (Ed. D. Dutton,
Proc. SPIE, California), vol.46, 1974.
[29] NAYYAR, V.P., Nouv. Rev. opt., vol.5, 1974.
[30] Mc KECHINIE, T.S., Optica. Acta., vol.20, 1973. [31] SOM, S.C., opt. Acta., vol.18, 1971.
[32] TOLANSKY, S.C. “High Resolution Spectro Scopy
(Mathuen & Co., Landon, 1947.
[33] CHATURVEDI, K.C. and SODHA, M.S., Indian J. Phys., vol.30, 1956.
[34] LUNEBERG, R.K., In “Mathematical theory of optics”. (Brown University,
Providence, Rhode Island), 1944.
[35] P. Thirupathi “Trade-Off between Detection and Resolution of Two Point Objects Under Various Conditions of Imaging Situations: Part-I: Mathematical Formulation of the Problem”, IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-

5728,p-ISSN: 2319-765X, Volume 6, Issue 5 (May. - Jun. 2013), PP

45-55.