International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 569
ISSN 2229-5518
The zero divisor graph of the ring Zpqr
Nazar H. Shuker1, Payman A. Rashed2
1College of computer Science and Mathematics, University of Mosul, Iraq
2 College of Basic Educations, University of Salahaddin, Iraq
Abstract- In this paper we construct a star zero divisor graph from the zero divisor graph of the ring Zy, y=pqr, where p, q, and r are prime number. The construction of the star zero divisor graph is results by removing some vertices from the zero divisor graph Γ(Zy), in different way, we used the simple way to get star zero divisor graph SΓ(Zy) by removing the zero divisors of the form nr, n from 1 to pq-1, except n=q. The aim of this work is to construct a star graph from the zero divisor graph of the ring Zy. Finally we proved that the zero divisor graph Γ(Zy) is three partite with girth three, while the diameter is less or equal 3.
Keywords- Commutative ring, zero divisor graphs, star zero divisor graph, girth.
—————————— ——————————
1- Introduction
Let R be a commutative ring with identity and let Z(R) be the set of zero- divisor of R. We associate a simple graph Γ(R) to R with vertices Z*(R)=Z( R)-{0} the set of non-zero zero divisors of R, and for distinct x, y 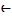 Z*( R), the vertices x and y are adjacent if and only if xy = 0 as a zero divisor elements. Note that Γ(R) is empty if and only if R is an integral domain, and the zero divisor graph is always simple undirected connected graph.
Z*( R), the vertices x and y are adjacent if and only if xy = 0 as a zero divisor elements. Note that Γ(R) is empty if and only if R is an integral domain, and the zero divisor graph is always simple undirected connected graph.
The concept of a zero divisor graph was first introduced by
Beck [3] in (1988), further studied by many authors like [1, 2, 3,
5, 8, 9] and [10]. In this work we consider the ring Zpqr, where p is prime and n is positive integer, and we construct a zero divisor star graph which will denoted by SΓ( R), where R 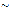 Zpqr .
Zpqr .
2-The zero divisor graph of the ring Z, y=2qr, where p=2, and q, r are primes.
The zero divisor graph of the ring Zy=Z2qr, where q,r are prime numbers, with 2 < q< r , q≠ r ( this condition is to avoid repeting rings of the same order) and the set of all non-zero zero devisers is defined as follow:
Z*(Zpqr ) ={p, 2p, 4p,….. (qr-1)p, q, 3q, 5q, ….. ,(pr-1)q, r, 3r, 5r,
…., (pq-1)} = ={2, 4, 6,….. 2(qr-1), q, 3q, 5q, ….. ,(2r-1)q, r, 3r, 5r,
…., (2q-1)}, with center C= 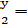 qr.
qr.
The zero divisor graph of this ring Zy denoted by Г(ZRyR),
y=2qr has the following five type of vertices of different degree.
1) The vertices vi, with deg(vi) = p-1 = 2-1 =1, are end vertices and they are (q-1) (r-1) vertices.
2) The vertices vj, with deg(vj) = q-1, they are (r-1) vertices for all j.
3) The vertices vk, with deg(vk)= r-1, they are (q-1) vertices for
all k.
4) The vertices vƖ, with deg(vƖ) = pq-1=2q-1, they are (r-1)
vertices for all l.
5) The vertices vm, with deg(vm) = 2r -1, they are (q-1) vertices
for all m.
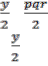
With center C= = =qr, deg(C) =qr-1 which is the greatest
degree vertex, ∆= – 1.
Next we shall give the following example.
Example-1: Consider p=2, q = 3, r =7, then the ring Zy = Z2.3.7 =
Z42, and the set of all zero divisors is Z*(ZR42R) = { 2, 4, 6, 8, 10, 12,
14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 3, 9, 15, 21, 27,
33, 39, 7, 14, 35}, with center C= 21 and they are exactly 30
vertices of five types.
vi= {2, 4, 8, 10, 16, 20, 22, 26, 32, 34, 38, 40}, are (q-1)(r-1) =(3-1)(7-
1) = 12 vertices, all of degree one ( they are end vertices adjacent
with the center C only), i.e. deg(vi) =1 for all i= 1, 2, …, 12.
vj={3, 9, 15, 27, 33, 39}, are (r-1)=(7-1)=6 vertices each of degree two, i.e. deg(vj) =(q-1) =(3-1) =2, since they are adjacent with the vertices of the partite set vm.
vk= { 7, 35} are (q-1) =2 vertices and they are adjacent with the vertices of partite set vƖ only, then deg(vk)= (r-1) =6 , and they are non adjacent with the center C. vƖ={6, 12, 18, 24, 30, 36} are (r-1) =2 vertices of degree pq-1 =2.3-1=5, i.e. deg(vƖ)=5, since they are adjacent with the vertices of the partite sets vƖ, vm and adjacent with the center C.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 570
ISSN 2229-5518

vm ={14, 28} they q-1 =2 vertices of degree 2r-1 =14-1 =13, i.e. deg(vm) =13 since they are adjacent with the ertices vj, vƖ rather than the center C, each zero divisor graph of the ring
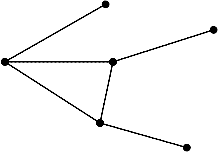
has those type of vertices with the similar degree as shown in the fighure (1) .
2-1 Construction of star zero divisor graph from the zero
divisor graph Г(Z2qr ).
This type of graph has only one center C= qr, thus the construction of star zero divisor graph from the basic graph Г(Z2qr ) is not difficult as the following example shows.
Example-2: The star zero divisor graph constructed from the zero divisor graph Г(Z y)= Г(Z2.3.7 )= Г(Z42 ) is shown in the figure (2) bellow after removing the vertices of vm={14,28}, where deg(14)=deg(28) =pr-1=13 and removing the vertices in vertex partite set vk={7, 35}, deg(7) =deg(35) =r-1 =6 . i.e. removing the vertices of the form nr, n from 1 to 5,(2q-1) except n=3, since center C=3r=21.
Theorem 2-1-1: The zero divisor graph Г(Z2qr ) is star graph by removing the vertices of the form vm and vk. i.e. vertices of degree 2r-1 and r-1, where vm is the partite set of vertices of greatest degree.
Proof: The vertices in the partite set vm are 2r-1 vertices the vertices with greatest degree, deg(vm) = 2r-1 they are (2r-1) vertices adjacent with the vertices in the partite sets vj and vƖ.
Clearly the vertices in vj are r-1 vertices of degree q-1 and they are non adjacent with center C but adjacent only with vertices in vm, so they falling (deleting) by removing the vertex partite set vm. While the vertices in the vertex partite set vƖ are r-1 vertices of degree 2q-1, after removing the vertex set vm, we remove most of the edges connect the vertices in vƖ with the general graph and other vertices are removed when we remove the vertex set vk which is adjacent with it except one edges represented the adjacency with the center. Thus we remove exactly q-1 vertices in each case, thus we get star zero divisor graph S1,m, m=deg(C) –(q-1)=deg(C )-q+1= C-1-q+1 = C-q and star graph is S1,C-1 .
Theorem 2-1-2:The zero divisor graph Г(Z2qr ) is 3-partite graph.
Proof: Up to the adjacency between the vertices in the given partite sets of different degree , we can divide the vertices in three partite sets such that V1 = C 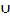 vj
vj 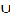 vk = { q, 3q, …, 3(pq-1), r, 3r,…, qr, (2q-1)r} , V2 = vi
vk = { q, 3q, …, 3(pq-1), r, 3r,…, qr, (2q-1)r} , V2 = vi 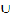 vƖ and V3 = vm , where the
vƖ and V3 = vm , where the
vertices in each partite vertex set Vi, i=1, 2, 3 are non adjacent
but there is connected vertices by an edge between the given
sets, so the graph is three partite graph.
3- The zero divisor graph of the ring Zy, y=3qr, where p=3 and q,r are primes.
C=21

2 4 6 8
10 12
16
18
20
22
24
26
30
32
The zero divisor graph of the ring Zy is Г(Z3qr), where p=3 and q, r>p, q≠ r. The zero divisor graph of the ring Z3qr is the same as the zero divisor graph Г(Z2qr ) for p=2, but has two centers C1 =qr and C2 =2qr, as shown in the following example.
Example-1: The zero divisor graph of the ring Zy =Zpqr, where p=3, q=5, and r=7 is denoted by Г(Z3.5.7 ) = Г(Z105 ), and has non- zero zero divisor elements in the zero divisor set Z*(Z105), as follow Z*(Z105) ={ 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42,
45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99,
34
40 38 36
Fig-2- star zero divisor S1,18
The vertices {3, 9, 15, 27, 33, 39} are of degree 2 and they are non adjacent with the center C and the vertices {7, 35} also non adjacent with center C, since 7.C=7.21=147 not divide 42, thus we remove only two edges from the center, then the degree of the center is decreases two and we get the star zero divisor S1,m=S1,18 , where m =deg(C)-2=20-2=18.
102, 5, 10, 20, 25,35, 40, 50, 55, 65, 70, 80, 85, 95, 100, 7, 14, 28, 49,
56, 77, 84, 91, 98}, they are 56 vertices of different degree with
centers C1 = qr =5.7 =35, and C2 = 2qr= 70.
In general the zero divisor set of the zero divisor elements of the ring Z3.qr is defined as follow:
Z*( Z3.qr) ={ 3, 6, …., 3( qr-1), q, 2q, 3q, ……, (3r-1)q, r, 2r, 3r, …, (3q-1)}, then up to the degree of the zero divisor vertices of the zero divisor set Z*, we can classify the vertices in Z* to the following partite sets as follow:
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 571
ISSN 2229-5518
1-The partite set V1 contains the vertices of the form np or 3n, n is positive integer from 1 to (qr-1) or multiple of 3 from 3 to y-3 except the vertices n(3q) , n from 1 to (r-1) and n(3r) , n from 1 to (q-1), all the vertices of degree two, since they are adjacent with the centers C1 and C2 only.
2- The partite set V2 contains the vertices of the form nq, n from
1 to (3r-1), except the vertices of multiple q and r, all the vertices
of degree (q-1).
(2q-2) vertices of degree (r-1) and they are adjacent only with the vertices in the partite set V4 ( the vertices of the form 3q), since nr.3q=3nqr and its divide 3qr. Removing this type of vertices dose not effect to the degree of the center C2 , so not effect to the degree of construction star graph since this type of vertices not adjacent with center, nr.2qr =2nqr2 not divide 2qr for n≠ multiple of 3. But we must remove these vertices to change the vertices in partite set V4 to the end vertices.
ii- The vertices nr , n is multiple of (3) till 3(q-1), ( the vertices
in V5 ) they are (q-1) vertices of degree (3r-1) and they are
3- The partite set V3 contains the vertices of the form nr, n from
adjacent with the centers C1
and C 2 , V4
and the vertices in
1 to (3q-1), except the vertices of the multiple 3 and q, they are 8
vertices of degree (r-1).
4- The partite set V4 contains the vertices of the form npq, {the reminder vertices in V1 (exception vertices fro V1) , where they are of the form n(3q), n from 1 to (r-1)}, they are (r-1) vertices of degree 2r or (3q-1).
5- The partite set V5 contains the vertices of the form npr, { the
partite set V2 , by removing these vertices all the remind vertices changed to end vertex ( vertex of degree one) thus we remove exactly (q-1) vertices from the center C2 , clearly the star graph is S1,m , m= deg(C) –(q-1) =C-1-q+1=C-q and S1,m=S1,C-q.
Theorem 3-1-2: The zero divisor graph Г(Z3qr ) is 3-partite graph.
Proof: Up to the adjacency of the vertices in the zero divisor
remind vertices of the partite set V2 , n(3r) , n from 1 to (q-1),,
graph Г(Z
3qr
) the vertices are divided in to three partite sets V i ,
they are (3r-1) vertices of degree (3r-1). With the centers C1 = qr,
V and V , and since the centers C
and C
are adjacent with the
j k 1 2
C2 = 2qr.
vertices in the partite sets V1 , V4
and V5 , then it may not be in
if p=3, then the ring is Z3.qr , q≠ r, and the zero divisor graph of this ring is denoted by Г(Z3.qr ).
3-1 Construction star zero divisor from the zero divisor graph
Г(Z3qr ).
Since this zero divisor graph is contains two centers, so to get the star zero divisor we must delete one of them and since they are have the same properties about the adjacency with the vertices are the degree, then the way deletion does not affect the quality of the star graph.
Now we can construct the star zero divisor graph S1,m from the zero divisor graph Г(Z y )=Г(Z3.qr ) by more than one way, first by removing the vertices of the form nr, n from 1 to (3q-1) except n = 2q , since 2qr = C2 , where they are (3q-2) vertices exactly. Second way by removing the vertices of the form nq, n from 1 to (3r-1) except n= 2q, since 2qr=C2 (the center), and they are (3r-2) vertices. But r ˃ q, means if we used the second way , we must remove more vertices from the zero divisor graph Г(Z3.qr ) to get the star zero divisor graph, then the best way for
the same part with the vertices in the above sets. We can
partition the vertices in the zero divisor set in to V i

= {C1 , C2 } 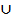 V2
V2 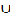 V3 , Vj = V1
V3 , Vj = V1 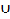 V4 and Vk = V5 such that the vertices in each vertex set are non adjacent but the vertices between the sets are adjacent. Clearly the zero divisor graph Г(Z3.qr ) is three partite graph as shown in the figure (3) below.
V4 and Vk = V5 such that the vertices in each vertex set are non adjacent but the vertices between the sets are adjacent. Clearly the zero divisor graph Г(Z3.qr ) is three partite graph as shown in the figure (3) below.
C1
V1
Vj
C2
V4 Vi
V2
V3
V5
Vk
getting the star zero divisor graph with greatest cardinality we
have the following theorem.
Theorem 3-1-1: The zero divisor graph Г(Z3qr ) is star graph S1,C- q by removing the vertices of the form nr, n =1,…, (3q-1) except
Fig-3, three partite zero divisor graph of Z3.qr
Theorem 3-1-3: The girth of the zero divisor graph Г(Z
three.
3.qr
) is
n= 3r.
Proof: The vertices nr = { r, 2r, …., (3q-1)r} which contains two kind of vertices with respect to the degree vertices they are in the partite sets V3 and V5 respectively:
i- The vertices nr, n is positive integer from 1 to (3q-1) except
the multiple of (3), i.e. the vertices in the partite set V3 , they are
Proof: As shown in figure (3) above , its seen that any cycle in the zero divisor graph when its constructed between two partite sets say V i and Vj its of the form V1 , C2 , V4 , C1 , V2 , it’s a cycle of length 4, but the cycle which is constructed between three partite sets is of the form V4 , C2, V5 , which is of the length
3, and by the definition of the girth the length of the smallest
cycle is a girth when its of length three, thus the girth is three.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 572
ISSN 2229-5518
Theorem 3-1-4: The diameter of the zero divisor graph is less than or equal 3. i.e. diam (Г(Z3.qr )) ≤ 3.
Proof: Since the diameter of any graph is the maximum distance between two vertices, and up to the zero divisor graph as shown in the figure (3) above, the distance of the different vertices in the different partite sets V i, Vj and V k is one or two if the vertices in two partite set, let x and y be two vertices in Vi and Vj respectively, then the shortest path between x and y is of length one or two, so diam(x,y)=1, or diam(x,y)=2. if x is a vertex in V1 in partite set Vj and y be a vertex inV3 in partite set Vj, then the shortest path between x and y is three and diam( x, y) =3, so diam(x,y) ≤ 3, for all x and y in the zero divisor graph.
(pr-1), where they are adjacent with the vertices in V2 , V4 and V6 .
6- V6 = { qr, 2qr, ..., (p-1)qr} or the vertices of the form nqr n from 1 to (p-1), they are (p-1) vertices of greatest degree (qr-1). They are called the centers of the zero divisor graph Г(Zpqr ),
Ci, i=1,2, …, (p-1). i.e. degree (C1 -1) = qr-1, where they are (p-1) vertices which are adjacent with the vertices in V1 , V4 and V5 . Clearly the union of these partite sets is the zero divisor graph Г(Zpqr ) , V1 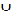 V2
V2 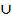 V3
V3 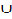 V4
V4 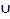 V5
V5 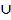 V6 = Z*(Zpqr) =V(Г(Zpqr )), the set of all vertices of the zero divisor graph Г(Zpqr ) and
V6 = Z*(Zpqr) =V(Г(Zpqr )), the set of all vertices of the zero divisor graph Г(Zpqr ) and
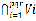
= Ø .where the adjacency relation between the partite set
4- The zero divisor graph Г(Zpqr ) For p prime, p˃ 3, p˂ q,r and
p≠ q ≠ r
of the zero divisor graph Г(Z
diagram bellow.
5.7.11
V1
) = Г(Z
385
) is shown in the
In general this type of zero divisor graph for p, q, and r prime has (p-1) centers and the zero divisor set of the zero divisor graph of the ring Zy, y =pqr is defined as follow:
Z*( Zy)= { p, 2p, 3p, …, (qr-1)p, q, 2q, …, (pr-1)q, r, 2r, 3r, …., (pq-1)r} with (p-1) centers such that Ci = nqr, n from 1 to (p-1) of greatest degree , all of degree (C1 -1). The vertices of this type of graph with respect to the degree of vertices are divided in to six partite sets (since the centers in the general form is (p-1) vertices we may put them in a partite set alone, but the center in the special case it was one or two, for this we didn’t put the centers
60 vertices of deg(4)
Ci
4 vertices of deg(76)
V5
6 vertices of deg(54)
24 vertices of deg(10) V3
V4
10 vertices of deg(54)
V2
40 vertices of deg(6)
in a partite set alone) as follow:
1- V1 = { p, 2p, 3p, …, (qr-1)p } or the vertices of the form np, n from 1 to (qr-1), except the vertices of multiple (pq) till (r-1)pq, and except the vertices of the form pr till (q-1)pr. The degree of these vertices is equal (p-1), since they are adjacent with the (p-1) centers of the zero divisor graph. And they are (pq-1)-(q-1)-(r-1) = (r-
1)(q-1) vertices.
2- V2 = { q, 2q, 3q, …., (pr-1)q} or the vertices of the form
nq, n from 1 to (pr-1) except the vertices of multiple p and r (except the vertices contained in the partite set V4 and V6). They are (p-1)(r-1) vertices of degree (q-1), they are adjacent only with the vertices in the partite set V5 , where they are (q-1) vertices exactly.
3- V3 = { r, 2r, 3r, …, (pq-1)r} or the vertices of the form nr n from 1 to (pq-1) except the multiple of p and q or except the centers C1 , …, Cp-1 vertices in V6 and the vertices in the partite set V5. They are (q-1)(p-1) vertices of degree (r-1), they are adjacent with only the vertices in the partite set V4 .
4- V4 = { pq, 2pq, …, (r-1)pq} or the vertices of the form
npq, n from 1 to (r-1), they are (r-1) vertices of degree
(pq-1) where they are adjacent with the vertices in the
The diagram of Г(Zpqr) = Г(Z5.7.11)
4-1 Construction of the star graph from the zero divisor graph

Г(Zpqr ).
This type of the zero divisor graph have (p-1) centers of greatest degree, in order to construct the star zero divisor graph, we take one of the centers in the zero divisor graph to be the center of the star graph. But when we take one of the centers say C1 , we must remove all the other centers to get the star graph. Since the centers are non adjacent so removing them, does not effect the degree of the center and so not effect the degree of the star graph. We have more than one way to get the star graph but we will choose the best way that is removing the smallest number of vertices from the zero divisor graphs as shown in the following theorem.

Theorem 4-1-1: the zero divisor graph Г(Zpqr ) is star graph S1,C-q
,by removing the vertices in the form in the partite sets V3 , V5 , and centers (p-2). i.e. the vertices of the form nr , r =1, …, (pq-1) except C1 ( the vertices nr included the centers too).
Proof: In this proof we depend on the diagram above, as in the
partite sets V3 , V5 and adjacent with the centers.
diagram the vertices in the partite set V3
are non adjacent with
5- V5 ={ pr, 2pr, …, (q-1)pr } or the vertices of the form
the center C1
, where the vertices in V3 is of the form nr, and
npr, n from 1 to (q-1), they are (q-1) vertices of degree
center C1 is qr, so nr.qr = nqr2 which is not divide the order of
the zero divisor graph, thus they are non adjacent. But after removing the vertices in the partite set V3 , the degree of the
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 573
ISSN 2229-5518
vertices in the partite set V4 decreases by (r-1). While the vertices in the partite set V5 are adjacent with the vertices in V2 , V4 and the centers Ci , and they are (q-1) vertices, then after removing the vertices in partite set V5 , the vertices in V2 will be fallen, and the degree of vertices of the set V4 decreases by (q-
1), by the number of vertices in the partite set V5 . Thus all other
vertices in remind sets changed to the end vertices, so we get star zero divisor graph S 1,m . But since we remove exactly (q-1) vertices from the center C1 ( the number of vertices in V5 is (q-
and y , and xz = yz =0, then the length of the path x─ y─ z is two . And so the vertices x, z and y, z may be in different partite sets, thus to connect the vertices to get the cycle, we have x─ y
─ z ─x is the cycle of length three, and by the definition of the
girth, implies that the girth of this graph is three.
And as in the diagram the smallest cycle in the zero divisor graph is of length 3, then the girth is three.
1)), then m=deg(C1 ) – (q-1) =C1 -1-q+1 =C1 -q and S1,m =S1,C1-q
Theorem 4-1-2:The zero divisor graph Г(Zpqr ) is 3- partite
Theorem 4-1- 4: The diameter of the zero divisor graph Г(Z
≤ 3.
pqr )
graph.
Proof: Depending on the partite sets given in the diagram above, and since the centers Ci, i=1, 2, .., (p-1) are non adjacent to gether, we can divided the zero divisor graph in to three partite sets such that the partite sets contains the vertices which are non adjacent as follow:
Vi = V1 + V4 = { p, 2p, 3p, …, (qr-1)p, pq, 2pq, …, (r-1)pq} = np, n
from 1 to qr-1 except the vertices of multiple of r.
Vj = V2 + V6 = { q, 2q, 3q, ……., (pr-1)q, qr, 2qr, …, (p-1)rq} =
nq, n from 1 to (pr-1) except the vertices of multiple of p.
Vk = V3 +V5 ={ r, 2r, 3r, …, (pq-1)r, pr, 2pr, …, (q-1)pr} = nr, n from 1 to (pq-1) except the vertices of multiple of q.
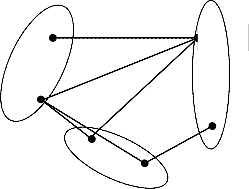
From the diagram bellow the vertices in the partite set are non adjacent , but there is adjacency vertices between the different partite sets. Up to the definition of the n-partite graph and the connection relationship between the vertices in the partite sets Vi, Vj, and Vk, the zero divisor graph Г(Zpqr ) is 3- partite graph as shown in the figure (4).
V1 C i
Vi
V4 Vj
V2
V5
Vk V3
Fig-4, Three partite zero divisor graph Г(Zpqr)
Theorem 4-1-3: The girth of the zero divisor graph Г(Zpqr ) is 3.
Proof: let x and y be two vertices in the graph Г(Zpqr ), if xy =0, then they are adjacent , since the graph is 3-partite , then x and y must be in different partite sets, and if xy≠ o, it means they are in the same partite set and there is no edge connect them
.suppose there exist z in the third partite set different from x
Proof: It's obvious, since the distance between the vertices in
different partite sets is one, two or three as shown in figure (4), then diam(x, y) ≤ 3.
References:
[1] S. Akbari , H. R. Maimani and S. Yassemi, " When Zero Divisor Graph is Planner or A Complete r-Partite Graph", J. of Algebra ,Vol.270, No.1 , pp. 169-180, (2003).
[2] D. F. Anderson , A. Frazier , A. Laune and P. S. Livingston "The Zero Divisor Graph of A Commutative Ring Π" Lecture note in pure and applied Mathematics , Dekker, Newyork, 220 , (2001).
[3] D.D. Anderson and P. S. Livingston, "The zero divisor graph of a commutative ring" . J. Algebra 217 (1999), pp. 434-
447.
[4] I. Beck, "coloring of commutative ring". J. Algebra 116
(1988), pp. 208 -226.
[5] V. K. Bhat and R. Raina, "A note on Zero Divisor graph Over Rings", International Journal Contemp. Math. Sci. ,Vol. 2, No.14, pp.667-671,(2007).
[6] F.Buckley and F. Harary. "Distance in Graphs". Addison- Wesley Publishing
Company Advanced Book Program, Redwood City, CA, 1990.
[ 7] J. A. Bondy and U. S. R. Murty " Graph theory and application" north – Holland, New York. Amsterdam, Oxford (2013).
[8] J. Coykendall, S.S. Wagstaff, L. Sheppardon and S. Spiroff, " On zero divisor graph". J. commutative Algebra 2(2012), pp.241-299.
[9] A. Duane, "Proper coloring and p- partite structures of the zero divisor graph" Rose Holman Undergraduate Math Journal
7, 2006.
[10] F. Harary, "Graph theory" Addison-Wesley publishing company, 1969.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 574
ISSN 2229-5518
[11] R. S. Gupta "The graph Γ2 (R) over a ring R" I. J.of Pure and
Applied Mathematics, 2013),Volume 86 No. 6,pp. 893-904.
[12] A. Ramin, " The total graph of a finite commutative ring"
Turk. J. Math 37 (2013), pp. 391-397.
[13] N. H. Shuker, H.Q. Mohammad and A.M. Ali, "The zero divisor graph of Zpnq" J. Algebra 6 (2012), pp. 1049-1055.
IJSER © 2015 http://www.ijser.org




