International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 1
ISSN 2229-5518
Study of Ion Sound Propagation Waves in
Thermal Plasma
Ghoutia Naima Sabri1*
Abstract— Plasma can support a great variety of wave motion. Both high frequency and low frequency, electromagnetic and electrostatic waves may propagate in plasma. The primary emphasis has been placed on the study of electrostatic waves because the ease with which such waves may be excited and detected and because the collisionless damping of waves predicted by Landau can be conveniently studied. In this paper we will discuss the propagation of ion sound waves in the collisionless thermal plasma by calculating the dispersion relation using fluid theory. The kinetic treatment shows clear that these waves are subject of strong Landau damping for weak temperature of ions compared to the one of electrons. The interest of this study can be applied to some astrophysical phenomena more precisely in the study of the generation of these waves in the topside ionosphere at low latitude sunrise and sunset.
Index Terms— Ion sound waves, thermal plasma, dispersion, fluid, kinetic, Landau, damping, temperature.
—————————— ——————————
N Plasmas, there are a variety of waves which propagate with a variety of nonlinear dispersion relations. We will ex-
The state of ionization of plasma is related to its temperature T
and density n and the degree of ionization which is defined by
amine one type of these waves and the approximations
needed to find its dispersion relation. Ion sound wave is a lon- gitudinal electrostatic wave in unmagnetized plasma arises from the motion of the ions by assuming that the frequency is low enough that ion can participate in motion. For small wave number k, it has the linear form of a normal sound wave. In this study we will discuss the propagation of these waves in non-collisional plasma, taking into account thermal effects. Thermal changes in wave propagation are not well described by fluid equations. To do this we will use the kinetic descrip- tion of plasma and the appropriate equation is the Vlasov equa-
tion.
In hot plasma, the dispersion function and its derivatives have
a wide range of applications in the descriptions of waves of small amplitude. It is also widely used in the description of polarization strongly inhomogeneous media. Accurate as- sessment of this function is important in various fields of science. Fried and Conte (1961) have presented interesting work on the main properties of the dispersion function of hot plas- ma.
IONISATION, SAHA LAW
In thermal plasmas, collisions between particles can cause io- nization if the energy difference between the particles is enough large (of the order of a few eV), or the recombination, if the energy difference is quite low.
As in the same ionized gas, the two forms of collisions can occur, a balance can be established. Just to maintain this bal- ance that the plasma is hot enough. It must even have a tem- perature of several tens of thousands of degrees [1], [2] eg stars and nuclear explosions.
(1) Where is the electron density, the ion density and neu- tral density. Because of collisions, atoms, molecules, or ions in the plasma can be ionized if the temperature is such that
(2)
is the ionization potential. If plasma is in thermodynamic equi- librium, the ionization is balanced by recombination. This balance is described by the Saha equation [3]. 
(3) Where is the neutral density, the density of ions et
is the balance between the ionization rate (depending on T) and the rate of recombination (depending on density) is Planck's constant (
) and corres- pond to the thermal wavelength of an electron ).
The term that contributes the most is
- If 
low ionisation, (industrial plasmas and ionosphere).
- If 
high ionisation, 
(thermonuclear plasmas and stellar).
Typically, begins to be meaningful when 
and allows distinguishing between weakly and strongly ionized plas- mas.
————————————————
*Ghoutia Naima Sabri is doctor in science physic, lecturer in University of
Bechar, Algeria, PH-0213773146965. E-mail: sabri_nm@yahoo.fr
IJSER © 2012 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 2
ISSN 2229-5518
50
0
-50
-100
-150
-200
-250
-300
0 0.2 0.4 0.6 0.8 1 1.2 1.4
Température
(8) The system consists of the Vlasov equations (4) and Max- well (5) - (8) is closed and called Vlasov-Maxwell system. In the absence of magnetic field applied from outside, the field 
will be zero (non relativistic case), the isotropic medium is called electrostatic and Lorentz force is reduced to an electrical force 
) and the system of Vlasov- Poisson [6] and the equation is written 
(9)
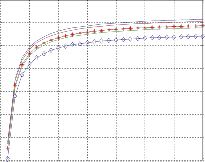
Fig.1. (a) The ionization of a fraction of hydrogen ( 
) in function of temperature and density (log scale).
It is easy to see that, according to an appropriate scale vari- able as the dispersion relation for electrostatic waves is ex- pressed by the dispersion function Z: 
(10)
Moreover, Z ( ) is the Hilbert transform of a Gaussian
[7],[8]. With 
and 
and
25
20
15
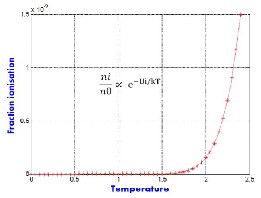
Fig. 1. (b) The ionization of a fraction of hydrogen (
) for a
constant density (Saha law). 10
Real(Z) Im(Z)
5
The analysis of the behaviour of particles moving in a hot plasma is based on the Boltzmann equation of the function of distribution
), also known as the Vlasov equation [4], [5]. This equation characterizes the evolution in time and space distribution of particles of non-collisional plasma in ki- netic description. For the species s, we can write a kinetic equ- ation of Vlasov in the form
(4)
This latter which is coupled to the Maxwell equations al- lows to describe the evolution of electric and magnetic fields. In the presence of electromagnetic field 
, Maxwell's equations are
(5) (6)
(7)
0
-5
-10
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Paramerter 
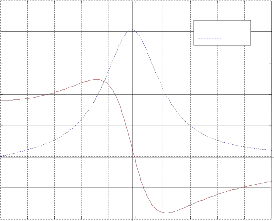
Fig. 2. Real (full curve) and imaginary (dashed curve) parts of plasma dispersion function Z ( )
As is shown on the figure 2, for Im( ) > 0, this function is defined in the upper half complex plane, the analytic con- tinuation in the lower half-plane is obtained by writing
(11)
and therefore the dispersion relation becomes
(12) With [8] 
. And the expression of Landau damping is given by:
IJSER © 2012 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 3
ISSN 2229-5518
10
(13) Ti
9 Te
8
6
The general kinetic dispersion relation for electrostatic waves
takes the form 3
2
1
w /k
(14)
And the Landau Damping is given by: Where
(15) (16)
0
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2
velocity (m/s)
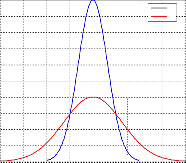
Fig. 3. Ion and electron distribution function f(v) with 
In fact, if 
then the wave phase velocity can lie on almost flat portions of the ion and electron distribution functions, as shown in Fig. 2, implying that the wave is subject to very little Landau damping. Indeed, an ion sound wave can only propagate a distance of order its wave-length without being strongly
The wave with a phase velocity, 
, is much less than the electron thermal velocity, but much greater than the ion ther- mal velocity. We may assume that 
for the ion term. It follows that, to lowest order, this term reduces to −
. Conversely, we may assume that 
for the electron
term. Thus, to lowest order we may neglect in the velocity
damped provided that is at least five to ten times greater than
.
Of course, it is possible to obtain the ion sound wave disper-
space integral. Assuming e to be a Maxwellian with tem-
sion relation, ω2/k2
= T2/mi, using fluid theory. The kinetic
perature , the electron term reduces to
(17)
treatment used here is an improvement on the fluid theory to
the extent that no equation of state is assumed, and it makes it
clear to us that ion sound waves are subject to strong Landau
damping (i.e., they cannot be considered normal modes of the
With λD is the Debye length [9] and ωpe the electron plasma frequency. Thus, to a first approximation, the dispersion rela- tion can be written
(18)
plasma) unless .
If we perturb and linearize the momentum equation and the con- tinuity equation for field free plasma [10], we get: 
(20) And
(19) For 
, we have 
, a dispersion rela- tion which is like that of an ordinary sound wave, with the pressure provided by the electrons, and the inertia by the ions. As the wave-length is reduced towards the Debye length, the frequency levels off and approaches the ion plasma fre- quency.
In the long wave-length limit, we see that the wave phase velocity is indeed much less than the electron thermal velocity
[by a factor ], but that it is only much greater than the ion thermal velocity if the ion temperature, , is much less than the electron temperature, .
(21)
Dotting the first equation (23) with 
and substituting into the second (24), we get:
(22)
and the dispersion relation is
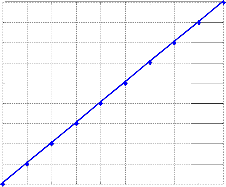
(23) With . This relation is shown on the Fig. 4. as a line which passed by the origin makes into account the pro-
portionality between ω and cs.
IJSER © 2012 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 4
ISSN 2229-5518
5
4.5
4
3.5
3
x 10-4
(28) while the electrons respond rapidly to the electric field, and so follow the Boltzman relation:
Thus
(29)
2.5
2
1.5
Rearranging, we get:
(30)
1
0.5
1 2 3 4 5 6 7 8 9 10
(31)
Wave vector k
Fig. 4. The dispersion relation 
Even if collisions are unimportant, sound waves, being longitu- dinal waves, generate density fluctuations which in turn generate electric fields that can provide the necessary restoring force.
When ion motion is involved, we know that the waves must be
low frequency, so we can use the plasma approximation, ne ≈ ni≈
n0. We are still assuming that there is no magnetic field [9], [10].
(24)
Thus if the ion and electron velocities differ, the densities will become different too. Thus the plasma approximation also
requires
(25)
1. It is essentially identical to the result for fluid sound waves even though at a microscopic level there are pro- found differences. The coupling here is electrostatic non collisional.
2. The electrons move very rapidly, and the distribution may
be assumed to be isothermal, γe = 1.
3. The electron mass is negligible compared with the ion
mass in the denominator.
However, Vlasov theory (a detailed study of the effect of the par- ticle velocity distributions) shows that the wave is strongly damped unless the electron temperature greatly exceeds the ion temperature. Thus the ion sound speed is determined by the elec- tron temperature and the ion mass.
(26)
We may now consider the electric field necessary to affect the
coupling. Poisson’s equation is:
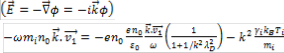
We should recognize the second term in the parentheses as 
. Now we rewrite the momentum equation for the ions, substitut- ing this expression for in the electric field term
.
(32)
(33)
where 
pi is the ion plasma frequency. The numerator in the second term is:
(34) Thus the new result is identical to the previous one except for the
denominator 
.
Thus the correction is necessary only when 
is not small, that
is when the wavelength is less than or equal to the Debye length. The full wavelength is within the region where we would expect the plasma approximation to fail. When 
we find 
and we have oscillations at the ion plasma frequency.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
(27) Now we allow for small differences between the electron and ion
densities. The ion density is given by the continuity equation:
0
0 0.5 1 1.5 2 2.5 3 3.5 4
kxdebye lenth (kxλD)
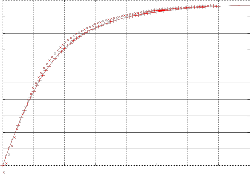
Fig 5: Dispersion relation for ion sound
IJSER © 2012 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 3, Issue 4, April-2012 5
ISSN 2229-5518
The wave reduces to plasma oscillations of the ions for which we obtain a graph of the dispersion relation as is shown on the Fig.5. similar to that of the Langmuir wave dispersion relation.
We have studied the ion-sound waves under the condition of
, in a hot, isotropic, and unmagnetized plasma modeled with the generalized 
distribution function. We have derived the dispersion relations for the ion-sound waves. It is possible to obtain the ion sound wave dispersion relation, 
, using fluid theory. The ki- netic treatment used here is an improvement on the fluid theory to the extent that no equation of state is assumed, and it makes it clear to us that ion sound waves are subject to strong Landau damping unless 
. For this condition the elec- trons are hot and an electrostatic wave in which ions do play a major role is found at lower frequencies. These waves are cha- racterized by phase velocities lying between the thermal veloc- ities of ions and that of the electrons and propagate only when ω
.
The present work can extended to study the generation of ion sound waves in the topside low latitude ionosphere at sunrise and sunset.
All praises and thanks are for Almighty ALLAH Who is the source of all knowledge and wisdom endowed to mankind and to the Holy prophet Muhammad (peace be upon him) who showed light of knowledge to the humanity as a whole.
[1] F. Mottez, “Equations plasmiques pour amateurs de machin-choses compliqués”, cour, 11 janvier 2008.
[2] N.G.Sabri, T.Benouaz, “Study of the Propagation of an electromagnetic wave in a Tokamak Plasma-Wave Plasma Interaction“.
"PhD Thesis, U. T, 200 pages, 2010.
[3] M.Moncuquet, “Cours Méthodes numériques de DESS, Laboratoire
d’Etudes Spatiales et d’Instrumentation en Astrophysique (LESIA), Paris
2001.
[4] P.Bertrand, “Description cinétique de la turbulence dans un plasma de Tokamak”, Ecole d’Aquitaine onde & matière, Maubuisson 2004.
[5] E.Sonnendrücker, “Approximation numérique des équations de Vla- sov-Maxwell”, Notes du cours de M2 ,2010.
[6] R. Fitzpatrick, “Course of the Physics of Plasmas”, the University of
Texas at Austin, 19-12, 2008.
[7] Westerhof, “Kinetic theory of plasma waves- homogenous plasma” ;
Transaction of fusion science and technology, Vol 49, Feb. 2006.
[8] J. Jiménez-Mier, “An aproximation to the plasma dispersion func-
tion”, Journal of quantitative Sectroscopy & Radiative Transfer 70 (2001) 273-
284.
[9] I.Weston, M.Stracey, Fusion plasma physics, WILEY-VCH, pp. 133-
134, 2005, ISBN-13:978-3-527-40586-2. (Book style)
[10] S.M.Lea, “Plasma Waves”, course; January 2007, unpublished.
IJSER © 2012 http://www.ijser.org