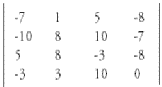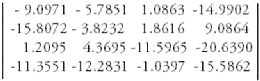International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1160

ISSN 2229-5518

Speech Signal Compression Using 2D Matrix

Decomposition Technique

Sharmiladevi.G, Jeyakumar.S

Abstract— Speech compression is a field concerned with obtaining compact digital representation of voice signals for the purpose of efficient transmission or storage. This paper develops the method of speech signal compression using matrix decomposition. The range of speech signals usually contains positive, negative and zero values. But for decomposition based compression, the samples should be nonnegative and nonzero values. This could be done by DC shifting. Assuming a sampling rate of 8000 samples per sec and processing window of 1ms, we have to deal with the set of 8 samples. The most negative value in this set will decide the amount of DC shift. 8 such consecutive 1ms windows are placed one below the other forming 8 row vectors of each 8 elements. This will lead to 8×8 samples represented in the matrix form. If we could find 1×8 row matrix multiplying with 8×1 column matrix, whose product of 8×8=64 values match

8×8 matrix of voice samples, then by simply transmitting the 8 elements of the column matrix and 8 of row matrix, we could recreate 64

product values at receiving end. The values of 8 elements of the column vector and 8 elements of row vector are obtained by iteration process. The RMSE and quality of recreated data are estimated in comparison with original data.

Index Terms— Matrix decomposition, DC shifting, Iteration method, Compression Factor, Quality analysis.

——————————  ——————————

1 INTRODUCTION

HE formal tools of signal processing emerged in the mid
20th century when electronics gave us the ability to ma-
nipulate signals – time-varying measurements – to extract
or rearrange various aspects of interest to us i.e. the infor- mation in the signal. The core of traditional signal processing is a way of looking at the signals in terms of sinusoidal com- ponents of differing frequencies (the Fourier domain), and a
set of techniques for modifying signals that are most naturally described in that domain i.e. filtering.
Although originally developed using analog electron- ics, since the 1970s signal processing has more and more been implemented on computers in the digital domain. Many tech- niques are used to compress the speech signal data such as run length encoding, Huffman coding [1], Lempel ziv encoding [2], etc. One dimensional compression methods are simpler than two dimensional methods. But compared with one di- mensional processing, two dimensional processing will give more compression. Matrix decomposition refers to the factori- zation of a given matrix into a row and column matrix form [3]. The outer product of row and column matrices is the given matrix. Matrix decomposition is a fundamental theme in linear algebra and applied statistics which has both scientific and engineering significance. The purposes of matrix decomposi- tion typically involve two aspects: computational convenience and analytic simplicity.
In the real world, it is not feasible for most of the ma- trix computations to be calculated in an optimal explicit way, such as matrix inversion, matrix determinant, solving

-------------------------------------------

• Sharmiladevi.G is currently pursuing Masters degree program in

Communication Systems in B.S.Abdur Rahman University, India, PH-

919677945516. E-mail: sharmi_gr@ymail.com

• Jeyakumar.S is currently pursuing Masters degree program in

Commnication Systems in B.S.Abdur Rahman University, India, PH-

919003065460. E-mail: jeymagnetron@gmail.com
linear system and least square fitting, thus to convert a diffi- cult matrix computation problem into several easier tasks such as solving triangular or diagonal system will greatly facilitate the calculations. Data matrices representing some numerical observations such as proximity matrix or correlation matrix are often huge and hard to analyze, therefore to decompose the data matrices into some lower-order or lower-rank canoni- cal forms will reveal the inherent characteristic and structure of the matrices and help to interpret their meaning readily [4], [5].
The fundamental matrix decomposition methods are
SVD, LU, QR and Eigen decomposition [6], [7] and [8].

2 PROCEDURAL ANALYSIS

The range of speech signals contain both positive, negative as well as zero samples. For decomposition method of com- pression the samples should be non negative and non zeros. This could be done by DC shifting by adding a significant val- ue to all elements to make them into positive values. At transmitter side, the audio signal is given as input to the sys- tem. These signals contain the samples. Then we form a square matrix by placing these samples row by row.
Fig.1 shows the audio signal containing both positive and negative samples.

International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1161

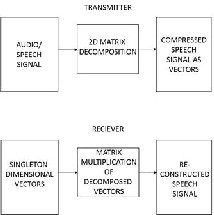
ISSN 2229-5518

The results are:
4x1 column matrix

1X4 row matrix

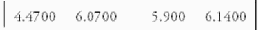
Fig.2 demonstrates the process of our proposed matrix de- composition method.
For example, if the most negative value is -50, then we have to add 51 to all samples to make all numbers into positive and avoid zeros. Then factorize the matrix by iteration method and find the row and column values which will give the most recre- ated matrix by multiplication. At receiver, undo the DC shifting by subtracting all elements by 51. All compression methods have inherent errors. These errors are squared, summed up and divided by total number of elements to find the MSE.

3 EXPERIMENTATION AND CALCULATIONS

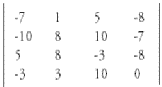
Consider a 4x4 random matrix. In the following ma- trix, samples are taken between negative 10 to positive 10.
.
Here, -10 is the most negative number. To make all samples into positive, add 11 to all samples.

After doing iteration process for above matrix we can get 1X4 row and 4X1 column factors. In transmission instead of sending 16 values of 4X4 matrix, we can send these row and column matrices which are only 8 values.
These are the matrices which will give the compressed val- ues. By multiplying these two matrices, we will get the recre- ated matrix at receiver side, which is,

At receiver side, undo the dc shifting by subtracting 11 from all samples. But we cannot get the exact original matrix. To find the error, we founnd the difference between recreated matrix and the original matrix, summed it, squared it and was divided by the total number of elements. This is called Mean Squared Error (MSE). Square root of the result gives Root Mean Squared Error (RMSE) [9].

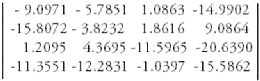
RMSE of the above matrix is 2.0610.
This is the simple example of matrix decomposition. Subse- quently, we have taken arbitrary random generated sampled data forming 32X32 matrix (1024 elements). It contains posi- tive, negative and zero samples. To make all samples into pos- itive, we do the DC shifting. And split the full 32X32 matrix into 64 matrices size of 4X4 matrix. We did the iteration pro- cess for all 64 matrices and found the MSE for the all matrices.
For cases when DC shifting are to be avoided, we can em- ploy non-negative matrix factorisations as like in [10], [11], and [12]

International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1162

ISSN 2229-5518

3 INFERENCES AND RESULTS

Adding MSE’s of all 64 matrices of 4X4 size and dividing by 64 will give us the overall MSE. Square root of the overall MSE gives the RMSE for entire 32X32 matrix. RMSE for 32X32 matrix in range between -10 to 10 is 1.5168.
The % RMSE is calculated as

=1.5168/ (10-(-10)) X 100
= .07584 X 100
=7.584%.
Generally for audio signal 10% is maximum acceptable er- ror and therefore, anything beyond 10% error cannot be effi- ciently reconstructed.

The compression factor is N/2 = 4/2 = 2. Therefore, we define the quality factor as,
= (2/7.58) x 100
=0.2637 X 100
= 26.37
When compression factor increases, quality will get poorer.

4 CONCLUSION

The proposed method of converting 1D data to 2D for factorization and compression can also be applied to other types of data like seismic data and SONAR data which can achieve better compression with the cost of error. However, methods like linear prediction can be employed in the areas of increased error to rectify it. The complexity of the proposed algorithm is that a signicant data indicating the type of data transformation to the receiver has to be transmitted along with the vector data which resists us from retaining a high Com- pression factor. Corresponding Truth tables at the receiver end can however reduce this complexity eventually.

ACKNOWLEDGMENT

The authors wish to acknowledge with thanks the help rendered by Dr. N. Nithiyanandam (guide), Dr. S. Kaja Mohideen, Dr. C. Tharini, Dr. P.K. Jawahar, Ms. A. Sumathi, Mr. H. Hasan Babu, Ms.Nallathai, Ms.Ayshathul Fouzia, and all others of School of Electrical & Communication Sciences, B.S.Abdur Rahman University, Chennai.

REFERENCES

[1] Khalid Sayood, “Introduction to Data Compression”, Morgan Kaufmann publishers, Elsevier Inc, pp 41-65, 2006.

[2] Khalid Sayood, “Introduction to Data Compression”, Morgan Kaufmann publishers, Elsevier Inc, pp 121-133, 2006.

[3] T. Kolda and B. Bader, “Tensor decompositions and applications,” SIAM Rev., vol. 51, no. 3, pp. 455–500, Sep. 2009.

[4] Siep Weiland and Femke van Belzen, “Singular Value Decompositions and Low Rank Approximations of Tensors”, IEEE Transactions on Signal Processing, Vol. 58, No. 3, March 2010.

[5] J. B. Kruskal, “Rank, Decomposition, and Uniqueness for 3-way and N-way arrays”, Elsevier Science Publishers, 1989.

[6] Misha Elena Kilmer and Carla D. Moravitz Martin, “Decomposing a Tensor”, workshop notes supported by AIM and the National Science Foundation,

2004.

[7] Carla D. Moravitz Martin, “Tensor Decompositions Workshop Discussion

Notes”, AIM, 2004.

[8] Brett W. Bader & Tamara G. Kolda, “Tensor Decompositions, the MATLAB Tensor Toolbox, and Applications to Data Analysis, Sandia National Laboratories, 2007.

[9] A.Beck and A. Ben-Tal, A global solution for the structured total least squares problem with block circulant matrices, SIAM J. Matrix Anal. Appl., 27 (2005), pp. 238–255.

[10] André Holzapfel and Yannis Stylianou, Musical Genre Classification Using Nonnegative Matrix Factorization-Based Features, IEEE Transactions on Audio, Speech, and Language Processing, Vol. 16, No. 2, February 2008

[11] P. Smaragdis, “Non-negative matrix factor deconvolution; extraction of multiple sound sources from monophonic inputs,” in Proc. 5th Int. Conf. Independent Compon. Anal. Blind Signal Separation, Granada, Spain, 2004, pp. 494–499.

[12] P. O. Hoyer, “Non-negative matrix factorization with sparseness constraints,” J. Mach. Learn. Res., vol. 5, pp. 1457–1469, 2004.