International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 1
ISSN 2229-5518
Sp-Separation Axioms
Alias B. Khalaf, Hardi A. Shareef
Abstract— In this paper Sp-open sets are used to define some new types of separation axioms in topological spaces. The implications of these separation axioms among themselves with some other separation axioms are obtained. Also their basic properties and characterizations are investigated.
Index Terms— Sp-open sets, pre separation axioms, semi-separation axioms.
—————————— ——————————
1 INTRODUCTION
he notion of semi-open sets which was introduced by Lev- ine in 1963 [5] is one of the well-known notion of general-
ized open sets. Several types of generalized open sets were introduced such as preopen sets [7] which was introduced by Mashhour et al in 1982. The notion of Sp-open sets [9] intro- duced by Shareef in 2007. In [6] Maheshwari and Prasad have defined the concept of semi-Ti, (i=0, 1, 2) spaces also in [3] Kar and Bhattacharyya defined new weak types of separation axi- oms via preopen sets called pre-Ti spaces for i=0, 1, 2 and in [4] Khalaf introduced strongly semi-separation axioms by us- ing special types of semi open sets.
In this paper we define new types of separation axioms called Sp-Ti spaces which are stronger than semi-Ti spaces and weak- er than strongly semi-Ti spaces (i=0,1,2).
2 PRELIMINARIES
Throughout this paper 
and 
will always denote topological spaces and 
will denote a function from a space 
into a space 
. If 
is a subset of , then the closure and interior of 
in 
are denoted by cl(
) and int(
) respectively. while Spcl(
) and Spint(
) denote the Sp-closure and Sp-interior of 
in 
re- spectively.
Definitions 2.1: A subset A of a space X is called:
1. semi-open [5], if 
⊆ cl(int(
)),
2. preopen [7], if 
⊆ int(cl(
)).
3. regular closed [11], if 
= cl(int(
)).
4. 
-semi-open [8], if for each 
, there exists a semi-open set 
such that 
cl(
)
.
5. Sp-open [9], if 
is semi-open and for each 
, there exists
a preclosed set 
such that 
.
————————————————
Author name: is currently one of the staff members of Department of
Mathematics, Faculty of Science, University of Duhok, Iraq
. E-mail: aliasbkhalaf@gmail.com
Co-Author name is currently pursuing Ph.D. degree program in Mathe-
matics Department, Faculty of Science, University of Sulaimani, Iraq.
E-mail: hardimath1980@gmail.com
The complement of a semi-open, preopen and Sp-open set is called semi-closed, preclosed and Sp-closed set respectively.
The family of all semi-open, preopen and Sp-open sets in a space 
is denoted by SO(
), PO(
) and SpO(
) respectively, while SC(
), PC(
) and SpC(
) denote the family of semi- closed, preclosed and Sp-closed sets in a space 
respectively.
Definition 2.2: A space 
is said to be:
1) Semi-T0 [6], (resp., pre-T0 [3], strongly semi-T0 [4] and
T0 [11]) space if for each two distinct points 
and
in 
, there exists a semi-open (resp., preopen, - semi-open and open) set containing one of them but does not contain the other.
2) Semi-T1 [6], (resp., pre-T1 [3], strongly semi-T1 [4] and
T1 [11]) space if for each two distinct points and 
in 
, there exist semi-open (resp., preopen, -semi- open and open) sets and containing 
and 
re- spectively, such that and 
3) semi-T2 [6] (resp., pre-T2 [3], strongly semi-T2 [4] and
T2 [11]) space if for each two distinct points 
and 
in 
, there exist two disjoint semi-open (resp., preo- pen, -semi-open and open) sets 
and 
containing 
and respectively.
Definition 2.3: [2] A function 
is said to be s- continuous or (strongly semi-continuous) if the inverse image of each semi-open set in 
is an open set in 
.
The following definitions and results are from [9].
Definition 2.4: Let 
be a space and let 
, then a subset 
of 
is said to be Sp-neighborhood of 
if there exists Sp-open set 
in 
such that 
.
Lemma 2.5: If a space 
is preT1-space, then SO(
) = SpO(
).
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 2
ISSN 2229-5518
Lemma 2.6: Every -semi-open set of 
is Sp-open set.
Theorem 2.7: Let 
be a space and 
. If 
, then
Spcl(
)⊆Spcl(
).
Lemma 2.8: The set 
is Sp-open in the space 
if and only if
for each 
, there exists an Sp-open set 
such that
.
Lemma 2.9: For any subset 
of a space 
, Spcl (
)=
SpD (
), where SpD(
) stands for the set of all Sp-limit points of 
in 
.
Theorem 2.10: Let 
be a regular closed subset of 
. If 
is an
Sp-open subset of 
, then 
is Sp-open in 
.
Theorem 2.11: Let f: 
be a homeomorphism. If 
SpO(
), then f ( ) SpO( ).
Theorem 2.12: A function f: 
is Sp-continuous if and only if for every open subset 
of 
, 
(
) is Sp-open in 
.
Theorem 2.13: Let f: 
be continuous and open function, then ( ) SpO( ) for any SpO( ).
Theorem 2.14: [5] Let 
and 
be two spaces and 
be the product space. If 
SO(
) and 
SO(
), then 
SO(
).
Theorem 2.15: [1] For any spaces 
and 
, if 
and 
, then 
(
.
3 SP-SEPARATION AXIOMS
Definition 3.1: A space 
is said to be:
1) Sp-To space if for each pair of distinct points in 
, there exists an Sp-open set in 
containing one of them and not the other.
2) Sp-T1 space if for each pair of distinct points and in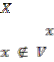
, there exists two Sp-open sets 
and in con- taining and 
respectively such that and
.
3) Sp-T2 space if for each pair of distinct points 
and 
in 
, there exists two disjoint Sp-open sets 
and 
in 
such that 
and 
.
Remark 3.2: From the above definition and Definition 2.2, it is clear that every Sp-Ti space is semi-Ti , for i=0, 1, 2. But the con- verse is not true in general as it is shown by the following ex- amples:
Example 3.3: Let 
and 
. Then SO(
) = 
and SpO(
) = 
. This implies that 
is semi-T0 space but not Sp-T0 .
Example 3.4: Let
and
. Then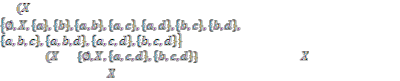
SO )=
and SpO ) = | . Hence, the space | is semi- |
T1 but not Sp-T1 also | is semi-T2 but not Sp-T2. | |
Remark 3.5: It is clear that every Sp-T2 space is Sp-T1 space and every Sp-T1 space if Sp-T0 space but the converse is not true in general as it is shown in the following examples.
Example 3.6: Let 
and 
. Hence
SO(
)
, and PC(
)
also
SpO(
) 
. Then 
is Sp-T0, but not Sp-T1 .
Example 3.7: Let 
be any infinite set equipped with the co- finite topology. Then 
is T1-space, so by Lemma 2.5, SO(
= SpO(
) and every infinite subset of 
is semi-open set. Hence 
is both semi-T1 and Sp-T1. But it is obvious that 
is not Sp-T2 space.
Lemma 3.8: Every strongly semi-Ti space is Sp-Ti space, for i=0,
1, 2.
Proof: Let 
be strongly semi-T0 space and let 
such that 
. Then there exists a 
-semi-open set 
containing one of them but not the other and since by Lemma 2.6, 
is Sp-open set containing one of them but not the other. This im- plies that 
is Sp-T0.
Similarly we can prove for i=1 and 2.
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 3
ISSN 2229-5518
The convers of Lemma 3.8 is not true in general as it is
shown in the example below:
Example 3.9: Let 
and 
, then SO(
) = 
, 
SO(
) = 
and SpO(
) = 
. Therefor, 
is Sp-T0 but not strong- ly semi-T0 space.
Proposition 3.10: If a space 
is Sp-T1 , then it is pre-T1 .
Proof: Let 
be an Sp-T1 space and let 
such that 
, so there exist two Sp-open sets 
and 
such that 
, 
and 
, 
. This implies that by Definition 2.1, there exist two preclosed sets 
such that 
and 
. Hence, 
and 
are preopen sets such that 
, 
and 
, 
. Therefore, by Definition 2.2, 
is pre-T1 .
The converse of Proposition 3.8 is not true in general as it is seen in the example below:
Examples 3.11: Let 
and
. Then
PO(
) =
and SpO(
) = 
. It can be checked that 
is pre-T1 but not Sp-T1.
The property of a space being Sp-T0 space is not hereditary property as it is shown in the following example :
Example 3.12: Let 
and 
,
then 
is Sp-T0 space and let 
and 
, then
SpO(
)=
. The subspace 
is not Sp-T0 subspace.
Proposition 3.13: The property of a space being Sp-Ti (for i=0,1,2) is a topological property.
Proof: Let 
be a homeomorphism and let 
be Sp-T0.
Suppose that 
such that 
. Since 
is onto so, there exist 
such that 
and 
and 
. Since 
is Sp-T0, so there exists an Sp-open set 
of 
containing one of the points 
and not the other. Since 
is homeomorphism, so by Theorem 2.11, 
is also Sp-open in 
and containing one of the points 
and not the other. Thus 
is also Sp-T0 space.
The proof for the space being Sp-T1 and Sp-T2 is similar.
Theorem 3.14: A space 
is Sp-T0 if and only if the Sp-closure of distinct points are distinct.
Proof: Let 
be Sp-T0 and 
such that 
. Since 
and 
is Sp-T0 , so there exists an Sp-open set 
contains one of them, say 
, and not the other. Then 
is Sp-closed set in 
contains 
but not 
, but Spcl(
) 
and since 
implies that 
Spcl(
), so Spcl(
) 
Spcl(
).
Conversely: To show that 
is Sp-T0 space, let 
such that 
. So by hypothesis, Spcl(
) 
Spcl(
), then there exist at least one point 
of 
which belongs to one of them, say Spcl(
) and does not belongs to Spcl(
). If 
Spcl(
), then 
Spcl(
) . This implies that, by Theorem 2.7, Spcl(
)
Spcl(
) which is a contradiction to the fact that Spcl(
) but 
Spcl(
), so 
Spcl(
). Hence, 
\Spcl(
) and 
\Spcl(
) is Sp-open set containing 
but not 
. Thus, 
is Sp-T0 space.
Theorem 3.15: A space 
is Sp-T1 space if and only if every sin- gleton subset of 
is Sp-closed .
Proof: Let 
be Sp-T1 space and 
. Let 
implies
that 
and since 
is Sp-T1 space so there exist two Sp-open sets 
and 
such that 
and 
, 
. This implies that 
, so by Lemma 2.8, 
is an Sp- open set . Hence, 
is Sp-closed .
Conversely: Let 
such that 
implies that 
are two Sp-closed sets in 
. Then 
and 
are two Sp- open sets and 
contains 
but not 
also 
contains 
but not 
this implies that 
is Sp-T1 space.
Theorem 3.16: For any space 
the following statements are equivalent:
1. 
is Sp-T1 space.
2. Each subset of 
is the intersection of all Sp-open sets containing it.
3. The intersection of all Sp-open sets containing the point
is the set 
.
Proof: (1) 
(2). Let 
be Sp-T1 and 
. Then for each 
, there exists a set 
such that 
and by Theorem
3.15, the set 
is Sp-open for every
. This implies that
so the intersection of all Sp-open sets containing 
is 
itself.
(2)
(3). Let 
, then 
so by (2), the intersection of
all Sp-open sets containing 
is 
itself. Hence the intersec- tion of all Sp-open sets containing 
is 
.
(3) 
(1). Let 
such that 
implies that by (3), the
intersection of all Sp-open sets containing 
and 
are 
and 
respectively, then for each 
there exists an Sp-open set
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 4
ISSN 2229-5518
such that 
and 
. Similarly for 
there exists
an Sp-open set 
such that 
and 
this implies that 
is Sp-T1 space.
Theorem 3.17: A space 
is Sp-T1 if and only if SpD(
) 
for each 
.
Proof: Let 
be Sp-T1 space and 
. If possible suppose that
SpD(
) 
implies that there exists 
SpD(
) and 
and since 
is Sp-T1, so there exists an Sp-open set 
in 
such that 
and 
implies that 
, then SpD(
) which is a contradiction. Thus SpD(
) 
for
each 
.
Conversely: Let SpD(
) 
for each 
, then by Lemma
2.9, Spcl(
)=
which is Sp-closed set in 
. This implies that each singleton set in 
is Sp-closed. Thus by Theorem 3.15, 
is an Sp-T1 space.
Lemma 3.18: If every finite subset of a space 
is Sp-closed , then 
is Sp-T1 space.
Proof: Let 
such that 
. Then by hypothesis, 
and 
are Sp-closed sets which implies that 
and 
are Sp-open sets such that 
and 
. Hence 
is Sp-T1 space.
Theorem 3.19: If 
is Sp-T0 space, then Spint(Spcl(
))
Spint(Spcl(
)) 
for each pair of distinct points 
and 
in 
.
Proof: Let 
be Sp-T0 and 
such that 
. Then there
exist an Sp-open set 
containing one of the point, say 
, and not the other implies that 
and 
, then 
and 
is Sp-closed . Now Spint(
)
Spint(Spcl(
))
this implies that 
Spint(Spcl(
))
, then 
Spint(Spcl(
)). But 
Spint(Spcl(
)), then Spcl(
)
Spint(Spcl(
)) this implies that Spint(Spcl(
))
Spcl(
)
Spint(Spcl(
)). Therefore, Spint(Spcl(
))
Spint(Spcl(
)) 
.
Theorem 3.20: If for each 
, there exists a regular closed set 
containing 
such that 
is Sp-T0 subspace of 
, then the space 
is Sp-T0.
Proof: Let 
be two distinct points in 
, then by hypothesis
there exists regular closed sets 
and 
such that 
, 
and 
, 
are Sp-T0 subspaces. Now if 
then the proof is complete but if 
and since 
is Sp-T0 subspace, so there exists an Sp-open set 
in 
such that 
and 
and since 
is regular closed set so by Theorem 2.10, 
is an
Sp-open set in 
containing 
. Thus 
is Sp-T0 .
Similar to Theorem 3.20, we can prove the following result. Theorem 3.21: If for each 
, there exists a regular closed set 
containing 
such that 
is Sp-T1 subspace of 
, then the space 
is Sp-T1.
Theorem 3.22: For a space 
the following statements are equivalent:
1. is Sp-T2 space.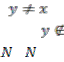
2. If , then for each there exists an Sp- neighborhood of such that Spcl(
).
3. For each , Spcl( ): is Sp-neighborhood of
.
Proof: (1) 
(2). Let 
be an Sp-T2 space and let 
, then for each 
there exist two disjoint Sp-open sets 
and 
such that 
and 
. This implies that 
, so by Definition 2.4, 
is an Sp-neighborhood of 
which is Sp- closed set in 
and 
implies that 
Spcl(
).
(2) 
(1). Let 
such that 
, then by hypothesis,
there exists an Sp-neighborhood 
of 
such that 
Spcl(
) implies that 
Spcl(
) and 
Spcl(
). But 
Spcl(
) is Sp-open set also since 
is Sp-neighborhood of 
, then there exists an Sp-open set 
of 
such that 
this implies that 
Spcl(
))
. Hence 
is Sp-T2 .
(2) 
(3). Let 
. If 
Spcl(
): 
is Sp-neighborhood of
, then there exists 
Spcl(
): 
is Sp-neighborhood of 
such that 
so by (2), there exists an Sp- neighborhood 
of 
such that 
Spcl(
) which is contradic- tion to the fact that 
Spcl(
): 
is Sp-neighborhood of 
. Thus 
Spcl(
): 
is Sp-neighborhood of 
(3) 
(2). Let 
so by hypothesis, we have 
Spcl(
): 
is
Sp-neighborhood of 
. Now if 
, then 
Spcl(
): 
is Sp-neighborhood of 
and hence there exists an Sp-neighborhood 
of 
such that 
Spcl(
).
Lemma 3.23: Let 
be a regular closed subset of the space, then any Sp-neighborhood of the point 
in 
is an Sp- neighborhood of 
in 
.
Proof: Let 
be any Sp-neighborhood of 
this implies that
by Definition 2.4, there exists an Sp-open set 
in 
such that
. Since 
is regular closed set in 
, so by Theorem
2.10, 
is an Sp-open set in 
which implies that 
is an Sp- neighborhood of 
in 
.
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 5
ISSN 2229-5518
Lemma 3.24: Let Y be a regular closed subspace of the space X
and A Y, then Spcl(A) Spcly(A).
Sp-open sets and 
. This implies that 
is
Sp-T2 space.
Proof: Let
x Spcly(A) implies that there exists an Sp-open
Theorem 3.28: For a space 
the following statements are
equivalent:
set U in Y containing x such that U A = . Since Y
is regular closed set in X then by Theorem 2.10, U is Sp-open
1. 
is Sp-T2 space.
2. The intersection of all Sp-clopen sets of each point in
set in X implies that
x Spcl(A), so Spcl(A) Spcly(A).
is singleton.
3. For a finite number of distinct points ( ),
Theorem 3.25: If for each point of a space there exists a
regular closed subset 
containing 
and 
is Sp-T2 subspace of
, then 
is Sp-T2 space.
Proof: Let 
, then by hypothesis, there exists a regular
Proof:
there exists an Sp-open set 
such that
( ) are pairwise disjoint.
closed set 
containing 
and 
is Sp-T2 subspace. Hence, by Theorem 3.22, we have 
SpclA(
): 
is Sp-neighborhood of 
in 
and since 
is regular closed set in 
, so by Lemma
3.24, Spcl(
)
SpclA(
) and by Lemma 3.23, 
is Sp- neighborhood of 
in 
, so 
Spcl(
): 
is Sp-neighborhood of 
in 
. Therefore by Theorem 3.22, 
is Sp-T2 .
Theorem 3.26: A space 
is Sp-T2 if and only if for each pair of distinct points 
, there exists an Sp-clopen set 
contain- ing one of them but not the other.
Proof: Let 
be Sp-T2 space and 
such that 
implies
that there exists two disjoint Sp-open sets 
and 
such that 
and 
. Now since 
and 
is Sp-open set implies that 
and 
is Sp-closed set, since 
is Sp-T2 space so for each 
there exists an Sp-open set 
such that 
, then by Lemma 2.8, 
is Sp-open set. Thus 
is Sp-clopen set.
Conversely: Let for each pair of distinct points 
, there exists an Sp-clopen set 
containing 
but not 
implies that 
is also Sp-open set and 
, since 
so 
is Sp-T2 space.
(1) (2). Let be Sp-T2 space and . To show is Sp-
clopen and 
. If 
is Sp-clopen and 
where 
. Then since 
is Sp-T2 space so there exists two disjoint Sp-open sets 
and 
such that 
and 
, implies that 
so by Lemma 2.8, 
is Sp-open set and also it is Sp-closed set this implies that 
is Sp-clopen containing 
but not 
which is a contradiction. Thus the intersection of all Sp-clopen sets containing 
is 
.
(2) 
(3). Let 
be a finite number of distinct
points of 
, then by (2), 
is Sp-clopen set and 
for 
. Since 
, for 
and 
, so there exists an Sp-clopen set 
such that 
and 
for 
, (
) implies that 
, where 
is also Sp-clopen set and 
. Therefore 
is Sp-open set containing 
, that is for each 
there exist pair- wise disjoint Sp-open sets 
for 
(
).
(3) 
(1). Obvious
Lemma 3.29: Let 
and 
be two spaces and 
be a product space. If 
SpO(
) and 
SpO(
), then 
SpO(
).
Proof: Let 
S O(
) and 
S O(
) implies that 
p p
Theorem 3.27: A space 
is Sp-T2 space if for any pair of dis- tinct points 
, there exists an Sp-continuous function 
of 
into a T2-space 
such that 
Proof: Let 
and 
be any two distinct points in 
. Then by
hypothesis there exists an Sp-continuous function 
from 
into a T2-space 
such that 
. But 
and since 
is T2-space so there exists two dis- joint open sets 
and 
such that 
and 
implies that 
and 
and since 
is Sp- continuous function, so by Theorem 2.12, 
are
SO(
) and 
SO(
), then by Theorem 2.14, 
SO(
). And now let 
, then 
and 
, but 
SpO(
) and 
SpO(
) so there exists pre- closed sets 
PC(
) and 
PC(
) such that 
and 
implies that 
and 
is preclosed set in the product space 
because by Theorem 2.15, 
(
)
(
) = 
(
). Thus 
SpO(
).
Theorem 3.30: Let 
be any finite family of
IJSER © 2012
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 6
ISSN 2229-5518
spaces. If 
is an Sp-T2 space for each 
, then the
product space 
is Sp-T2 .
Proof: Let 
and 
be any two distinct points in 
, then 
for some 
. Suppose that 
and since 
is Sp-T2 space for each 
, so there exist two disjoint Sp-open sets 
and 
in 
such that 
and 
. Then by Lemma 3.29, 
and 
are Sp-open sets in 
such that 
, 
and 
= 
. Hence
borhood of each of it’s points, so 
is open set. Thus 
is
closed set in 
.
Corollary 3.33: If 
and 
are s-continuous (or strongly semi- continuous) functions on a space 
into an Sp-T2 space 
and the set of all points 
in 
such that 
is dense in 
,
is closed in 
, that is = cl( ) and from the hypothesis is dense implies that cl( ) =
. Therefore, for all 
. Hence .
is Sp-T2 .
Theorem 3.31: Let 
be an open continuous function. If 
is an Sp-T2 space, then the set 
is an Sp-closed set in the product space 
.
Proof: Let 
. It is enough to show
is an Sp-open set, so let 
, then 
. But 
and 
is Sp-T2 space, so there exist two disjoint Sp-open sets 
and 
such that 
and 
implies that 
and 
and since 
is open and continuous function, so by Theorem 2.13, 
and 
are disjoint Sp-open sets in 
, then by Lemma 3.29, 
is an Sp-open set in 
. Hence, 
and therefore by Lemma 2.8, 
is an Sp-open set in 
. This implies that 
is an Sp-closed set in 
.
Theorem 3.32: If 
and 
are s-continuous (or strongly semi- continuous) functions on a space 
into an Sp-T2 space 
, then the set of all point 
in 
such that 
is closed set in
.
Proof: Let 
. It is enough to show that 
is an open set in 
. So let 
, then 
and 
, but 
is Sp-T2 space, hence, there exist two dis- joint Sp-open sets 
and 
in 
such that 
and 
. Since 
and 
are s-continuous functions and 
, 
are semi-open sets, so by Definition 2.3, we obtain that 
and 
are open sets containing 
. This implies that 
and 
is open set also. Now let 
then we must show that 
. If possible, suppose that there exists one point 
but 
, then 
. Therefore, 
and since 
, then 
and 
. This implies that 
and 
, but 
so 
which is
contradiction. Thus 
implies that 
is a neigh-
REFERENCES
[1] N. K. Ahmed, On some types of separation axioms, M. Sc. Thesis, Sala- haddin University, 1990.
[2] S. Jafari and T. Noiri, Decompositions of S-continuity, Far East J. Math. Sci.
Special Volume (1997), Part II, 253-256.
[3] A. Kar and P. Bhattacharyya, Some weak separation axioms, Bull. Cal.
Math. Soc., 82 (1990), 415-422.
[4] A. B. Khalaf, On some strong types of separation axioms, J. Dohuk Univ., Vol. 3, No. 2, 76-79, 2000.
[5] N. Levine, Semi-open sets and semi-continuity in topological spaces, Amer.
Math. Monthly, 70 (1963), 36-41.
[6] S. N. Maheshwari and R. Prasad, Some new separation axioms, Ann. Soc.
Sci. Bruxelles, 89 (1975), 395-402.
[7] A. S. Mashhour, M. E., Abd El-Monsef and S. N. El-Deeb, On pre- continuous and weak precontinuousm appings, Proc. Math. and Phys. Soc. Egypt , 51 (1982), 47-53.
[8] T. Noiri, On S-closed and S-perfect functions, Atti della Acad. Delle Sci.
Torino, (1986), 71-79.
[9] H. A. Shareef, Sp-open sets, Sp-continuity and Sp-compactness in topologi- cal spaces, M. Sc. Thesis, Sulaimani University 2007.
[10] L.A. Steen and J. A. Seebach, Counterexamples in Topology, Holt, Rinehart and Winston, Inc., New York, 1970.
[11] S. WILLARD, General Topology, Addlson-Wesley Publishing Company,
1970.
IJSER © 2012
http://www.ijser.org