International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 173

ISSN 2229-5518

Some Aspects of Chess Game Relating to Knot

Theory

S. I. Nada & A. I. Elrokh

Abstract— In this paper we present an analysis for the movement of chess pieces and explain how it relates to the theory of knots. We show that for each piece in the chess except pawns, one can form a sequence of steps to construct a specific knot.

Index Terms— Knots, Cyclic graph, Chess.

1 INTRODUCTION

——————————  ——————————
HESS is a game with deep historical origins dating back as far as the 6th century AD, and first version of the game emerged in India under the name of Chaturanga.
Then the game quickly spread to Persia and subsequently the Arab world. Eventually spread to Europe. Although the game is thought to have differed widely from the game we play to- day, around the end of the 15th century many of the chessmen developed their modern powers, enhancing the speed and dynamics of the game and creating the game we play now. At the beginning of each game the chessboard is set up in the initial position. Each player begins with 8 pieces (1 King, 1
Queen, 2 Rooks, 2 Bishops and 2 Knights) and 8 pawns which are located in their respective positions.
Knot theory deals with knots, links, braids, and related ob- jects. It is a branch of algebraic topology which started in the late 1880’s. The scotch mathematician, Lord William Thom- son( 1824-1907), proposed that different elements consists of different configurations of knots. He described atoms to be knots in the fabric of this ether. This theory led many Scientists to believe that we could understand the chemical elements by simply studying different types of knots and thus this led to a completely new field of study in Mathematics .One of the most important applications of the knot theory arises in study of DNA[4]. It was discovered in 1953 by James Watson and Francis Crick that the basic structure of DNA molecules con- sists of two stands which are twisted together in a right- hounded helix. The geometric of DNA can exist in linear form or in closed circular form. It is known that the circular form of DNA can be knotted and two or more circular DNA forms can be linked together. Many other application of Knot theoryin particle physics can be found in [7], [8], statistical mechanics [6], Islamic and Pharaohs Arts[1], and more. [9], [10], [11].The Feynman relativistic chessboard model provides a representa- tion of the solution to Dirc equation in (1+1)-dimension space

————————————————

• Mathematics Department, Faculty of Science, Menoufia University, Egypt.

time of quantum mechanics[ ]. A reformulation of the Feyn- man chessboard model has been made by Ord [ ]. Also, there is a relation between this model and stochastic model of the Telegraph equation[ ]. It is proved that this mode l was em- bedded in correlations stochastic model [ ].

2 BASIC DEFINITIONS AND TERMINOLOGY

A knot K is a subspace of the three dimensional Euclidean
space ℝ3, which is a topological image of the circle s1 ( as an embedding ) k ∶ s1 → ℝ3 of the circle s1 into three dimen- sional Euclidean space ℝ3. Some examples are illustrated

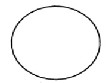
down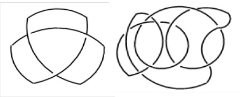
Circle s1 (unknot) trefoil knot some more complicated knot
A knot can be taken with or without orientation. In the fol-

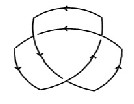
lowing ,we mainly consider oriented knots as seen below
Oriented s oriented trefoil
A link graph, or shortly link, L is an embedding of a topologi-
cal sum of finitely many copies of a circle s1 into ℝ3, L: s1 ∪
s1 … ∪ s1 → ℝ3. The restriction of L to one of the copies of s1

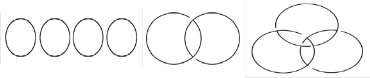
is called a component of L, see the attached figure.
n-unlink (s1 ∪ s1 ∪ … ∪ s1 )2-chain Borromean rings
A diagram of a knot or link is a projection of the latter into a
plane with marking of each crossing (under-crossing or over
crossing) in the image of the projection. That means a knot
diagram is picture of a projection of knot onto a plane, a dia-

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 174

ISSN 2229-5518

gram in ℝ2 is made up of a number of arcs and crossing . At
a crossing, one arc is over pass and the other is under pass,

and it is not allowed the following cases :

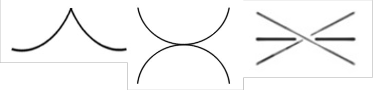
Graph of a diagram of a knot or link is the graph consisting of the crossings as the vertices of the graphs and the edges are the arcs between two each crossings. In other words: A graph 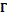is a link graph (knot-graph) if there is a link 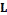(knot 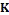) such that suitable projection of 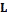(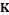) which gives 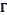. It is de-
noted by Γ(L)�Γ(K)�.

Two graphs 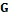and H are said to be isomorphic (written G
H) if there are two bijections θ: v(G) → v(H) and φ: E(G) → E(H) such that ψ(G(e)) = uv if and only if ψH �φ(e)� − θ(u) θ(v); such a pair (θ, φ) of mappings is called an isomor- phism between 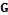and H. A knot K0 is equivalent to a knot Kn if there exists a sequence of knots K1 , K2, … , Kn−1 such that Ki is an elementary deformation of Ki−1 for 1 ≤ i ≤ n. A
prim knot is a knot that is indecomposable. Specifically, it is a
non-trivial knot which cannot be written as the knot sum of
two non-trivial knots [17]. Knots that are prime are said to be
composite. Finally, a prime link is a link that cannot be repre-
sented as a knot sum of other link [15], [16].

MAIN RESULTS

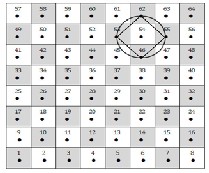
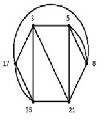
The movement of the king (one step only in any direction) is as seen in Fig. (1) , from square (vertex) 4 to 12, then to 3 and next back to 4 . Repeating these movements give the at- tached graph which is isomorphic to a cycle and in return rep-

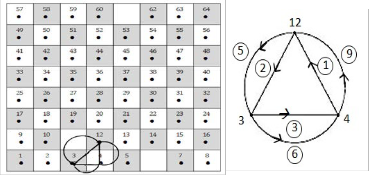
resents the trefoil knot 31 .
Fig. (1)
Fig. (2)
The knot 41 is represented by a sequence of the king move-
ment:
4 → 12 11 → 4 → 3 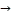12 → 11 → 34 , and then repeating these

movements once; see Fig. (3).
Fig. (3)
This is a cyclic graph that is isomorphic to knot 41 .
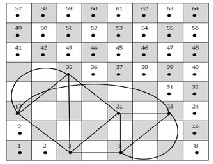
For knots 52 one can have the sequence of the king move-
ments:
60 → 53 44 → 45 → 53 60 → 52 → 45 → 44 → 52 → 60 ,

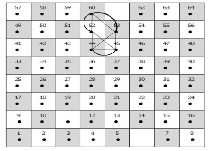
andthen repeating these movements; see Fig. (4).

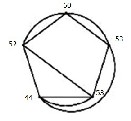
Fig. (4)
The knot 63 can be represented by the sequence of the king
movements:
4 → 12 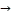13 → 21 → 20 13 → 4 → 11 → 20 → 21 → 12 → 11
→ 4, and then repeating these movements; see Fig. (5).
Another knot namely 42

can induced from the following:
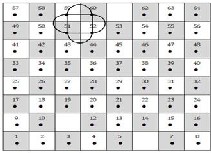
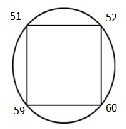
King movements: 60 → 52 → 51→ 59 ⟶ 60 . Repeating these
movements we will gain a cyclic graph which is isomorphic to
knot 42. See in Fig .(2)
Fig. (5)

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 175

ISSN 2229-5518

It should be noticed that if n = 2 i.e, the king moves from one
square to neighbor square and return back to the original
square will gain a link graph with two components. In case
≥ 3, we get the following :

THEOREM (1) :

A link graph corresponding to a knot with n-gone , n ≥ 3 can
be obtained from a sequence of king’s movement.

PROOF :

First of all, it should be mentioned that for n = 1,2 we don’t
have any knot. The simplest closed path for the king move-
ments is 3 steps, vertical, horizontal and 45° direction in any
order and then by repeating this sequence we get 3-gone link
graph corresponding to trefoil knot. Suppose that, closed path
for the king movement with (n-1) steps give an (n-1) gone
knot. It clear that one step movement for the (n-1) gone knot
contain at least one step direction45° . In this case to add an-
other movement, we must delete one of the previous move-
ment first and then add two movements one of them at least
with 45° direction and that gives us an n- closed path and by
returning back we get the required n- gone. This completes
our proof.
Fig. (6)
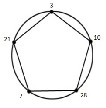
Another way of movement for the Bishop is the following:
7 → 28 10 → 3 → 21 7 → 21 → 3 → 10 → 28 → 7.Repeat this once more to get a cyclic graph which is isomorphic to 51 ; See
Fig. (7).

THEOREM (2):

3 3

Any link graph without multiples (61 , 818 , 10123, 121 , … ) can-
not be obtain from any sequence of the king movement.

PROOF :

Fig. (7)
Now, let us study some models for the Rook:
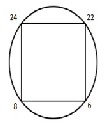
Let us have the following consecutive movements: 8 → 6 22
→ 24 → 8. Repeat them once more to gain the cyclic graphic

3 3 2

It is well known that {61 , 121 , … } forms link graphs with three
components and no multiples [18], and the rest of knots which
are 818 , 10123, … are with one component and no multiples. In
either case any given closed path will contain at least two ver-
tices with degree less than 4. We assert that these two vertices
are not located in two adjacent square in the chess, otherwise
by connecting them will get a multiple which is not allowed. If
the two vertices are not located in two adjacent squares, then
the king has no authority to make one movement to connect
them. Thus the theorem is proved.
For the movement of Bishop(moves with angle 45° only) and
Rook (moves horizontally or vertically only).
Let us first discuss the Bishop movements models:
Suppose the sequence of its movements are as follows:
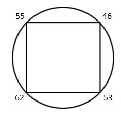
62 → 53 46 → 55 62.Repeating these movements we will gain a cyclic graph which is isomorphic to knot 42. See in Fig.
(6).

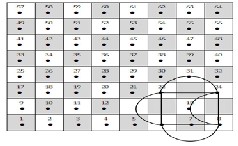
which is isomorphic to41 ; See Fig. (8).
Fig. (8)
Another sequence of movement for the Rook is the following:
7 → 28 10 → 3 → 21 7. Repeating these movement we will gain a cyclic graph which is isomorphic to knot 51; see Fig. (9).

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 176

ISSN 2229-5518

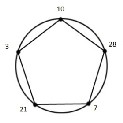
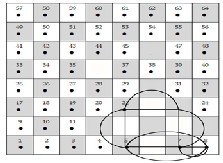
Fig. (9)
square to closed one. Then its next movement is from what closed, not the beginning closed square. This shows that we need another two steps to return to the original square.
For the Queen's movement, we demonstrate twelve move- ments’ models corresponding to different kinds of knots.
The first model is the following sequence:
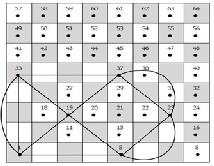
5 → 14 13 → 5 , and by repeating these one again to have a cyclic graph that is isomorphic to knot 31 ; see Fig. (11).

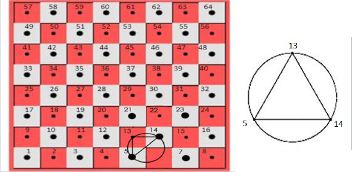
THEOREM (3) :

Any link graph with n-gone corresponds to the Rook’s move-
ment or the Rook’s movements is constructed if ≥ 4.

PROOF:

It a clear that any shortest closed path can be constructed from the Rook’s movements or Bishop’s movements by four steps (square or rhombus) then to make a knot from any of them it needs to return it back and consequently this will construct a knot with 4- gone. This completes the proof.
For the Knight movement, It is known that its movement takes the form of letter L, this means that if Knight is in the white square, then its next move will be in a black square. So, the horse's movement will get several black and white squares.
Some of its movements were analyzed as follows: 7 → 24 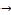30
→ 13 → 7. And by repeating these movements we will have a

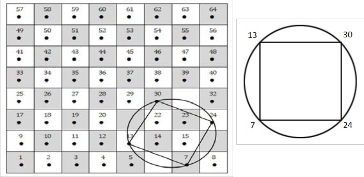
cyclic graph which is isomorphic to knot 42 ; see Fig (10) .
Fig. (10) Thus we come to the following :

THEOREM(4):

Any knot with n-gone associated with the knight’s movements is constructed only if n is even.

PROOF :

Since the behavior of the knight’s movement takes the shape of the letter L, the first move of the knight goes from a white square to a black square or vise verse. Whiteout any loss of generality, let us suppose that its first movement from a white
Fig. (11) The second model is the following:
5 → 14 21 → 12 → 5. Then repeat these movement again to get a cyclic graph that is isomorphic to knot 41 ; see Fig .(12).

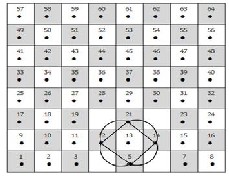
Fig. (12)
The third model is the following sequence of movements:
5 → 7 21 → 23 → 7 5 → 23 21 → 5. The induced cyclic graph will be isomorphic to knot 41; see Fig. (13).

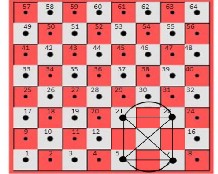
Fig. (13)
The fourth model is the following sequence of movements:
5 → 14 30 → 28 → 19 5 . Then repeating these one again to have a cyclic graph that is isomorphic to knot 51; see Fig .(14).

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 177

ISSN 2229-5518

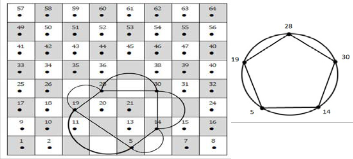
Fig. (14)
The fifth model is the following sequence of movement:
5 → 12 21 → 19 → 21 5 → 3→ 12 19 → 3 5, and then

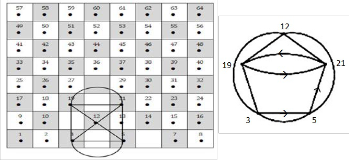
repeating these movement ; see Fig. (15).
Fig. (15)
This a cyclic graph which isomorphic to knot 52 .

The sixth model is the following sequence of the movement:
5 → 32 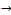53 → 32 → 5 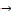29 → 53→ 26 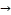29 → 26 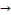5, and this
repeating these movements; see Fig. (16).

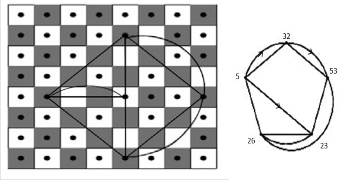
Fig. (16)
This a cyclic graph which isomorphic to knot S2 .
The seventh model is the following sequence of the move-
ment:
5 → 21 23 → 5 → 3 35 → 21→ 3 17 → 35 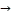17 → 23→ 5 ,
and then repeating these movements; see Fig. (17).
Fig. (17)
This is a cyclic graph which isomorphic to knot 63.
The eighth model is the following sequence of the movements:
5 → 23 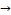47 → 29 → 47 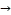23 → 5→ 2 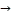29 → 26 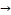2 → 26→ 5,

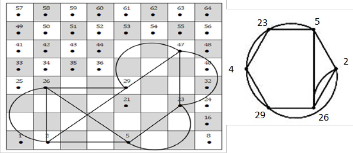
and then repeating these movements; see Fig. (18).
Fig. (18)
This a cyclic graph which isomorphic to knot 61.
The ninth model is the following sequence of the movements:
5 → 23 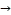37 → 23 → 5 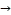19 → 37→ 33 1 → 33 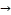19 → 1→ 5,

and then repeating these movements; see Fig. (19).

Fig. (19)
This a cyclic graph which is isomorphic to knot 63 .
The tenth model is the following sequence of the movements:
5 → 23 39 → 23 → 5 3 → 39→ 53 35 → 3 35 → 53→ 5,

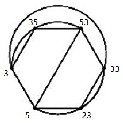
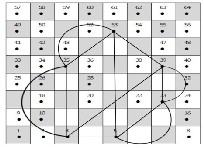
and this repeating these movements; see Fig .(20).
Fig. (20)

This a cyclic graph which isomorphic to knot 62 .

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 178

ISSN 2229-5518

The eleventh model is the following sequence of the move- ments:
5 → 14 30 → 23 → 21 12 → 30→ 21 5 → 12 14 → 23→ 5,
and this repeating these movements; see Fig. (21).

Fig. (21)
This a cyclic graph which isomorphic to knot 63.

The last model is the following sequence of the movements:

5 → 23 37 → 19 → 12 30→ 21 14 → 5 37 → 6→ 14
23 → 19 21 → 12→ 5, and this repeating these movements;
see Fig. (22).

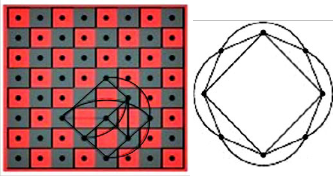
Fig. (22)
This is a cyclic graph which is isomorphic to knot 818.
Any single movement by any piece of the chessboard ,except
the knight, can also be done by a single movement of the queen. One movement for the knight can be reached by two steps queen’ movements to reach same position. Taking into consideration all what we have previously discussed, one can conclude the following

THEOREM (5):

Any knot can be represented by a sequence of the queen’
movements.

CONCLUSION AND SUGGESTION:

For each piece in the chess except pawns ,one can form a se- quence of steps to construct a particular knot. The Feynman relativistic chessboard model provides a representation of the solution to Dirc equation in (1+1)-dimension space time of
quantum mechanics[ ]. A reformulation of the Feynman
chessboard model has been made by Ord [ ]. The Chessboard model to a fully four-dimensional space-time of the high ener- gy physics [ ] is still to be studied. This is extremely a new field relating the chessboard and knot theory with quantum filed theory.

REFERENCES

[1] A. I. Elrokh, Graph, knots and links. Ph. D. Thesis. Uni. Ernst- Mortiz- Arndt

Greifswald Germany ,2004.

[2] J. A. Bondy, U.S.R. Murty, 1982, Graph theory with applications, New York.

Amsterdam. Oxford 5th printing..

[3] B. Sanderson, Lecture in knot theory, 1997.

[4] K. Murasugi , Knot theory and its applications, Boston[u.a]: Birkhuser, 1996.

[5] W. B. RtaymondLickorich, An introduction to knot theory, Springer-verlage,

1997.

[6] R.J. Baxter, Exactly solved Models in Statistical Mechanics, Acadmic press,

1982.

[7] T. P. Cheng and L. F. Li., Gauge theory of elementary particle Physics, Clar- endon Press-Oxford, 1988.

[8] H. Jehle, Flux quantization and particle Physics, Phys. D. vol. 6, no. 2,pp. 441-

457, 1972.

[9] L. H. Ryder, Quantum field theory, Cambridge Uni. Press, 1985.

[10] D. W. Sumners, Untangling DNA, Math. Intelligencer, Vol. 12,no. 3,pp. 71-

80.1990,

[11] P. A. M. Dirac, The principles of quantum Mechanics, Oxford Uni. Press, 1958. [12] L. K. Kuffmann, On knots, Annals of Mathematics Studies 115, Princeton Uni.

Press, 1987.

[13] J. W. Alexander, G. B. Briggs, On types of knotted curves, Ann. Of Math. (2)

28(192627), no. 1-4, 562-586.

[14] K. Reidemeister, Elementare begruendung der knot en theorie, Abh. Math.

Sem. Uni. Hamburg 5 (1926), 24-32.

[15] H. Doll, and J. Hoste, A tabulation of oriented link, Math. Comput. 57, 747-

761, 1991.

[16] D. Rolfsen, Knots and Links, Wilmington, DE: Publish or Perish press ,1976. [17] H. Schubert, Die eindeutige Zerlegbarkeit eines Knotens in Primknoten, S. B.

Heidel-bergerAkad. Wiss. Math. Nat. Kl. (1949), 57-104. [18] The Rolfsen knot table” katlas.org/wiki/main_page

Our idea is not far from this direction
R. P. Feynman, Space-time approach to non-relativistic quan- tum mechanics, Rev. Mod. Physics, 20, 1948
M. Kac, A stochastic model related to the telegrapher's equa- tion, Rocky Mountain Journal of Mathematics, 4, 497-509, 1974
A reformulation of the Feynman chessboard model, » Journal of Statistical Physics , » Volume 66, Issue 1-2 , pp 647-659 , G. N. Ord ,1992.
M. S. El Naschie, “A Review of E-Infinity and the mass Spec-
trum of High Energy Particle Physics,” Chaos, Soli- tons & Fractals, Vol. 19, No. 1, 2004, pp. 209-236