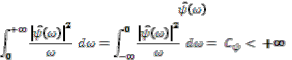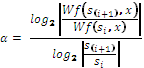International Journal of Scientific & Engineering Research,Volume 3, Issue 6, June-2012 1

ISSN 2229-5518

Performance analysis of life time efficiency of Machines using Wavelet Transform Modulus Maxima

Dr.P.Venkatakrishnan, S.Sangeetha, M.Muthukumaran

Abstract.Machinery health monitoring is a key step in the implementation of maintenance in industry. A remarkable property of the wavelet transform is its ability to characterize the local regularity of machines. In mathematics, this local regularity is often measured with Lipschitz exponents (LE). The singularity, by means of a Lipschitz exponent of a function, is measured by taking a slope of a log- log plot of scales and wavelet coefficients along modulus maxima lines of a wavelet transform [1]. In this paper, we applied singularity analysis with wavelet for data processing and a new concept, Lipschitz exponent function, was proposed based on wavelet transform. The results show that objective based LE demonstrates excellent performance.

Keywords:Singularity analysis; Wavelet and Lipschitz exponent

————————————————————

1 INTRODUCTION

Singularities and irregular structures often carry the most important information in machines health. Because singularity often carries the most important information contained in a machine, singularity analysis has emerged as a multiple-area problem solving method in recent years [2], [3], [4], [5], [6] and [7]. In mathematics, the singularity is usually measured with Lipschitz exponent (LE). It is a real number that can characterize the local regularity or smoothness in a signal. The definition of LE is given in [1]. Thesignal

singularity refers to the intermittent points or discontinuous derivative of the signal. In mathematics, the sharpness of an edge can be described with Lipschitz Exponent. Local lipschitz can be efficiently measured by wavelet transform. The relationship between the modulus of wavelet transform and lipschitz exponent can be described as theorem 1.The WTMM representation of a signal records the values and locations of local maxima of its wavelet transform modulus. They proved that the local lipschitz exponent of a signal can be estimated by tracing the evaluation of its WTMM across scales. From the estimated lipschitz exponent and with some other a priori information of the signal, an effective denoiseing method can be developed. Although the WTMM based algorithms give a promising performance in many aspects, the irregular sampling nature of the WTMM complicates the reconstruction process. This paper is organized as follows. The wavelet transform and a tutorial review on lipschitz exponent are briefly introduced in section II. The Lipschitz exponent measuring with WTMM is presented in section III. In section IV, we present the experiment procedure to measure the LE from WTMM and result analysis is presented in section V. Finally, section VI gives some concluding remarks.

2. Fundamental Concepts:

A. Continuous Wavelet Transform (CWT):

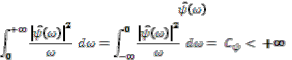
The formalism of the continuous wavelet transform was first introduced by Morlet and Grossman [8]. Let ψ (t) be a com- plex valued function. The function ψ (t) is said to be a wavelet
if and only if its Fourier transform satisfies

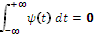
(1) This condition implies that
(2) The continuous wavelet transform of a function f(t)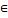

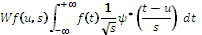
L2(R) with respect to the wavelet ψ (t) is defined as
(3)
where ψ* denotes the complex conjugate of ψ.
A wavelet ψ (t) is said to have n vanishing moments if

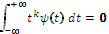
and only if for all positive integers k < n, it satisfies,
(4) A popular wavelet in practice is the nth derivation of
the Gaussian function

(5) When performing wavelet singularity analysis, the number of vanishing moments is very important, as it provides an upper bound measurement for singularity characterization.

B. Singularity detection with wavelet:

Lipschitz exponent is a measurement of the strength of a singularity. Mallat and Hwang [1] showed that the LE can

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research,Volume 3, Issue 6, June-2012 2

ISSN 2229-5518

be computed by WTMM of signals.

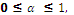
Singular exponent: A function f(x) is said to be lipschitz α, for
at a point x0, if and only if there exists a constant
A such that for all points x in a neighborhood of x0

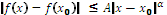
(6) The function f(x) is uniformly lipschitz α for any x0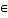(a,b) and x 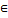(a, b). We say that f(x) is singular in x0 if it is not Lipschitz 1 in x0. If a function is Lipschitzα , for α > 0, then it is conti- nuous in x0. If f(x) is discontinuous in x0 and bounded in a neighborhood of x0, then it is lipschitz 0 in x0. If f(x) is conti- nuously differentiable then it is lipschitz 1 and thus not singu- lar.
We suppose that the ψ (t) has a compact support, is n times continuously differentiable and is the nth derivatives of a smoothing function. The theorem 4 of [1] can be rewritten as: Theorem 1:
Let f(x) be a tempered distribution whose wavelet
transform is well defined over (a, b), and let x0 Є (a, b). We suppose that there exists a scale s0> 0, and a constant C, such that for x Є (a, b) and s < s0, all the modulus maxima of Wf(s, x) belong to a cone defined by

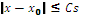
(7) Then, at all points x1 Є(a, b), x1 ≠ x0 ,f(x) is uniformly Lipschitz n in a neighborhood of x1. Let
α < n be a non-integer. The function f(x) is lipschitz α at x0 , if
and only is there exists a constant A such that at each modulus
maxima (s, x) belong to a cone defined by (7)


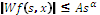
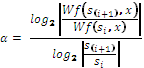
(8) By substituting Si and Si+1 into equation (9), throughout simple derivation, lipschitz exponents can be expressed in the follow- ing form
(9)

3. LE Measuring with WTMM:

Based on theorem 1, there are some existing methods used to estimate LE [1][4][12][14]. Equations (6) and (8) imply that
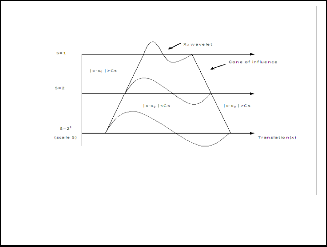
|Wf(s, x)| ≤ O(sα) inside a cone |x-x0| ≤ Cs [1], where C is the support of the mother wavelet. This cone is the so-called “cone of influence” (COI), as shown in Fig.1. Mallat and Hwang furthered [1, Th.4] and proposed to estimate the lip- schitz exponent of a singularity by tracing its WTMM curves across scales inside the COI. They showed that the local regu- larity of certain types of non-isolated singularities in the signal can be characterized by using the WTMM. They also showed that the decay of the expected WTMM value of a wide noise
across scales is proportional to 1/2j , where s=2j .This means that the WTMM curve of noise are expected to decay across scales at least at a rate of 1/2j or even not propagate to coarser
scales .This is not the case for regular signals and edges .Since signals edges possess zero lipschitz exponents and regular signals possess positive lipschitz exponent , the corresponding WTMM will be the same, if it does not increase , when scale increase. Equ(8) is equivalent to


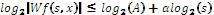
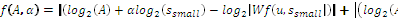
(10) (11)

If the wavelet transform maxima satisfy the cone distribution imposed by theorem 4,in[1],(10) proves that the lipschitz regu- larity at x0 ,is the maximum slope of straight lines that remain above log |Wf(s, x)|,on a logarithmic scale. The fact that all modulus maxima remain in a cone that points to x0 also im- plies that f(x) is lipschitz n at all points x Є +a, b*, x≠ x0x)

Figure. 1. “cone of influence”(s, x) plane of the wavelet function (

C )in different scales.

4. Lipschitz exponent (α) measurement proce- dure:

From the Theorem.1, we can measure the Lipschitz exponent
using the following algorithm:
1. Compute straight line l(log2(s)) connecting (log2(s small), log2|Wf(u ,s small)|) and (log2(sma x), log2|Wf(u, s max)|). If l(log2(s)) ≥ log2|Wf(u, s)|, return the intercept log2(A) and slope α of l(log2(s)), go to 7),otherwise, go to 2).
2. Let s=smax and f(A,α) = C, where C is a constant large
enough.
3. Compute tangent l(log2(s)) at (log2(s), log2|Wf(u,s)|).
If l(log2(s)) ≥ log2|Wf(u,s)|, go to 4). Otherwise go to
6).

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research,Volume 3, Issue 6, June-2012 3

ISSN 2229-5518

4. Compute (11), record the result f of (11) and the in- tercept log2(A) and slope α of l(log2(s)). If f <f(A,α), f(A,α) = f and LE = α.
5. If s = smin, go to 7). Otherwise go to 6).
6. s =s-Δlog2(s), go to 3
7. Output LE = α.

5. Result Analysis:

Theorem 1 proves that the wavelet transform is par- ticularly well adopted to estimate the local regularity of func- tion. When a function is approximated at a finite resolution, strictly speaking, it is not meaningful to speak about singulari- ties, discontinuities and Lipschitz exponents. This is illu- strated by the fact that we cannot compute the asymptotic de- cay of the wavelet transform amplitude at scales smaller than one. In this work we used the function f(x) shown in Fig.2 will be used for testing the capabilities of the wavelet to determine the regularity.
accurate value. Because we use the appropriate known edge of α, algorithm searches the optimal result along log2|Wf(u,s)| curve only, and the problem of initialization of A and α can be

avoided. The adopted wavelet ψ(x) is the second derivative of a Gaussian function. We denote Ssmall=2 Smax=64 and Δlog2s=0.0326, and for this method we adopt the initial func- tion values A=2 and α=1.


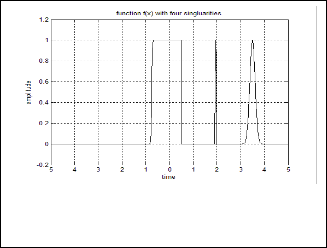
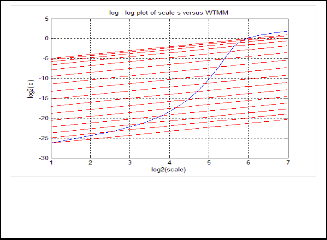
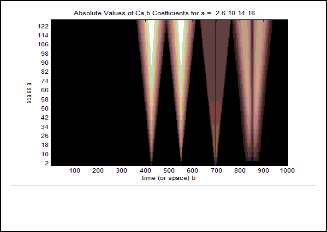
Figure 3. Continuous Wavelet transform of function f(x)
Figure.2. Function f(x) with four singularities

at abscissa 413, 551, 696, and 802.
Figure 4.log - log plot of scale s versus WTMM with tangent line
Continuous Wavelet transform of function f(x) shown
in Fig.3. In Fig.3, the discontinuity appears clearly from the fact that |Wf(s, x)| remains approximately constant over a large range of scales, in the neighborhood of the abscissa 551. A negative lipschitz exponent corresponds to sharp irregulari- ties where the wavelet transform modulus increases at fine scales. At the abscissa 696, the signal of Fig.2 has such a dis- crete Dirac. The wavelet transform maxima increase propor- tionally to s-1, over a large range of scales in the corresponding neighborhood.
The log-log plot of scale s versus WTMM shown in
Fig.4, then to find the slope of corresponding scale and coeffi- cient line using lipschitz exponent (α) measurement proce- dure. We determined lipschitz exponent function (α) and compared refer Table.1. LE with objective function is more
Fig.5. Mechanical diagnostic test bed.

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research,Volume 3, Issue 6, June-2012 4

ISSN 2229-5518

TABLE 1

COMPARISON OF LE (Α ) WITH HAWANG AND OBJECTIVE

FUNCTION.

6. Conclusion:

We proved that the wavelet transform modulus maxima detect all the singularities of a function and we described strategies to measure their Lipschitz regularity. This mathematical study provides algorithm for characterizing singularities of irregular structures such as the multiracial structures observed in phys- ics and mechanical systems. In this paper, we applied a new signal processing technique, singularity analysis with wavelet, to determine the Lipschitz exponent function using wavelet transform. In future work shown in Fig.5, we apply Lipschitz exponent function into machinery health monitoring process using cumulant based health index (CHI). This information can also be used for machine remaining life prediction, which is an important area that has been investigated by many re- searchers.

REFERENCES

[1] s. Mallat and W. L. Hwang, "Singularity detection and processing with wavelets," IEEE Trans. Inf Theory, vol. 38, no. 2, pp. 617-643,Mar. 1992

[2] A. Arneodo, E. Bacry, and J. F. Muzy, "The themodynamics of fractals revisited with wavelets," Phys.A., vol. 213, pp. 232-275, Jan.1995

[3] H. Asada and M. Brady, "The curvature primal sketch," IEEE Trans.Pattern Anal. Mach. Intell., vol. 8 no. 1, pp. 2-14, Jan. 1986

[4] C. L.Tu and W. L. Hwang,"Analysis of singularities from modulus maxima of complex wavelets," IEEE Trans. Inf: Theory, vol. 51, no. 3, pp.

1049-1062, Mar. 2005

[5] S. Mallat, A Wavelet Tour of Signal Processing. San Diego, CA: Aca- demic, 1999

[6] S. Mallat and S. Zhong, "Characterization of signals from multiscale edges," IEEE Trans. Pattern Anal. Mach. Intell., vol. 14, no. 7, pp. 710 -732, Jul. 1992

[7] J. Zhang and C. X. Zheng, "Extracting evoked potentials with the sin- gularity detection technique," IEEE Trans. Biomed. Eng., vol. 16, no.5 ,pp.

155-161, sep 1997.

[8] E. Chassande-Mottin and P. Flandrin, "On the time-frequency detection of chirps," Appl. Compute. Harmonic Anal., vol. 6, pp. 252- 281, 1999

[9] H. B. Nugraha and A. Z. R. Langi, "A procedure for singularity mea- surement using wavelet," in Proc. IEEE Int. Conf Circuits and Systems. Bali, Indonesia, Oct. 2002.

*10+. K. Berkner and R. Wells, “A new hierarchical scheme for approximat- ing the continuous wavelet transform with applications to Edge dete c- tion”, IEEE Signal processing letters., vol.6, no.8, Aug.1999.

Dr. P.Venkatakrishnan currently working as Head of the department in electronics and communication engineering in Vickram College of Engi- neering, Enathi-630 561, Tamilnadu, India PH-+91-9003775807. E-mail: venkatakrishnan@vickramce.org

Mrs.S.Sangeetha currently working as Assistant Professor in Electrical

and Electronics Engineering Department, Kamaraj College of Engineerng

and Technology, Virdhunagar, Tamilnadu.PH-9003775808. E-mail: vick- ee_geetha@yahoo.com

K.Muthukumaran currently working as Assistant Professor in electronics and communication engineering in Vickram College of Engineering, Ena- thi-630 561, Tamilnadu, IndiaPH-+91-9791812341. E-mail: muthukuma- ran@vickramce.org

IJSER © 2012

http://www.ijser.org