INTRODUCTION
Wormholes are handles or tunnels in the spacetime topology connecting two separate and distinct regions
of spacetime. These regions may be part of our Universe or of different Universes. The static and spherically symmetric traversable wormhole was first introduced by Morris and Thorne in their classic paper [1]. From the stand point of cosmology,the cosmological constant Λ, served to create a kind of repulsive pressure to yield a stationary Universe. Zel’dovich [2] identified Λ with the vacuum energy density due to quantum fluctuations. Morris-Thorne wormholes with a cosmological constant Λ have been studied extensively, even allowing Λ to be replaced by a space variable scalar field. These wormholes cannot exist, however, if Λ are both space and time dependent. Such a Λ will therefore act as a topological censor.
In this article, we introduce an exact black hole solution of the Einstein field equations in four dimensions
with a positive cosmological constant to electromagnetic and conformally coupled scalar fields. This solution is often called a Martinez-Troncoso-Zanelli (MTZ) black hole solution. In agreement with recent observations [3], this black hole only exists for a positive cosmological constant Λ, and if a quartic self-interaction coupling is considered. Static scalar field configurations such as those presented here, which are regular both at the horizon as well as outside, are unexpected in view of the no-hair conjecture [4]. The conformal coupling for the scalar field is the unique prescription that guarantees the validity of the equivalence principle in curved spacetime [5]. In the literature, a number of traversable wormhole solutions with cosmological constant are available [6-21]. A general class of wormhole geometries with a cosmological constant and junction conditions was analyzed by De Benedictis and Das [9], and further explored in higher dimensions [10]. It is of interest to study a positive cosmological constant, as the inflationary phase of the ultra-early universe demands it, and in addition, recent astronomical observations point to Λ > 0 . Lobo [12], with the intension of minimizing the exotic matter used, matched a static and spherically symmetric wormhole solution to an exterior vacuum solution with a cosmological constant, and he calculate the surface stresses of the resulting shell and the total amount of exotic matter using a volume integral quantifier [13]. The construction of traversable wormhole solutions by matching an interior wormhole spacetime to an exterior solution, at a junction surface, was analyzed in [13-15]. A thin-shell traversable wormhole, with a zero surface energy density was analyzed in [15], and with generic surface stresses in [14]. A general class of wormhole geometries with a cosmological constant and junction conditions was explored in [9], and a linearized stability analysis for the plane symmetric case with a negative cosmological constant is done in [17].
Morris-Thorne wormholes, with Λ = 0, have two asymptotically flat regions spacetime. By adding a positive cosmological constant Λ > 0 , the wormholes have two asymptotically de-Sitter regions, and by adding a
negative cosmological constant,
Λ < 0 , the wormholes have two asymptotically anti-de Sitter regions. We
analyze asymptotically flat and static traversable Morris-Thorne wormholes in the presence of a cosmological
construct. An equation connecting the radial tension at the mouth with the tangential surface pressure of the thin- shell is derived. The structure as well as several physical properties and characteristics of traversable wormholes due to the effects of the cosmological term are studied.
This article is organized as follows: In Sec. II we studied Einstein’s field equations and total stress-energy with a cosmological constant Λ. In Sec. III, we introduce an exact black hole solution with electromagnetic and conformally coupled scalar fields. The junction conditions and the surface tangential pressure are discussed in Sec.
IV. Specific construction of wormhole with generic cosmological constant is discussed in Sec. V. Finally, conclusion of the results is given in Sec. VI.
EINSTEIN’S FIELD EQUATIONS AND SURFACE STRESSES WITH A COSMOLOGICAL CONSTANT Λ
Form of the Spacetime Metric
The interior spacetime metric for the wormhole in the static and spherically symmetric isotropic coordinate ( t, r,θ ,φ ), is given by [1]
ds 2
= −e2Φ (r ) dt 2 +
dr 2

+ r 2 (dθ 2 + sin 2 θdφ 2 ) , (1)
1 −
b(r )
r
where Φ(r) is denoted as the redshift function, for it is related to the gravitational redshift and
b(r) is called the
form function, as it determines the shape of the wormhole; both are functions of the radial coordinate. For the traversable wormhole, one must demand that there are no horizons present, which are identified as the surfaces with
e−2Φ
→ 0 , so the
Φ(r)
must be finite everywhere. The radial coordinate has a range that increases from a
minimum value at
r0 , corresponding to the wormhole throat to a . Maximum value of a corresponding to the
mouth at r0 one has to join smoothly this spherical volume to another one copy with r ranging again from r0 to a . In addition, one has then to join each copy to the external spacetime from a to ∞ , as will be done.
The details of subsequent mathematics and of physical interpretations will be simplified using a set of
orthonormal basis vectors as the proper reference frame, the observers remain at rest in this coordinate system ( t, r,θ ,φ ), with ( r,θ , φ ) constant. The basis vectors in this coordinate system are denoted by et , er , eθ , eφ . The
transformation of these basis vectors from the proper reference frame to a boosted frame is as follows:
−φ
et = e
et ,
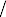
erˆ = (1 − b
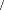
r
r )1 2 e
e
= r
e
−1
θˆ θ
and
φˆ
e = (r sin θ )−1
eφ . (2)
In this basis the metric coefficients assume on their standard, special relativity forms are given by
gµˆνˆ = eµˆ .eνˆ = ηµˆνˆ = diag (−1,1,1,1). (3)
In the orthonormal reference frame, the Einstein field equation with a generic cosmological constant can be written as
Gµˆνˆ + Ληµˆνˆ = 8πG Tµˆνˆ . (4)
The Total Stress-Energy Tensor with a Cosmological Constant
One may write the Einstein field equation with a cosmological constant in the following manner;
Gµˆνˆ
= 8πG (Tµˆνˆ
µˆνˆ
+ T (vac ) ), (5)
T
(vac )
where µˆνˆ
![]()
= −gµˆνˆ (Λ
(8πG)), is the stress-energy tensor associates with the vacuum, and in the orthonormal
reference frame is given by
µˆνˆ
T (vac ) = diag [Λ![]() (8πG)− Λ
(8πG)− Λ![]() (8πG)− Λ
(8πG)− Λ![]() (8πG)Λ
(8πG)Λ![]() (8πG)]. (6)
(8πG)]. (6)
For the metric (1), the non-zero components of the Einstein tensor in the orthonormal reference frame can be written as [1]
Gtˆtˆ
b′
![]()
= , (7)
r 2
![]()
G = − b +
21 −
b Φ′
![]()
![]()
, (8)
rˆr
r 3
r r
G ˆ ˆ
= G ˆ ˆ
= 1−
b
![]()
Φ′ −
b′r − b
![]()
![]()
Φ′ + (Φ′)2 + Φ′ −
b′r − b
![]()
. (9)
θθ φφ
r
2r(r
b)
r 2r 2 (r
b)
Using the Einstein field equations with a non-zero cosmological constant in an orthonormal reference frame, we obtain the following stress-energy scenario
τ (r) =
− 21 −
Φ′
![]()
![]()
− Λ , (11)
1 b b
![]()
3
8πG r
( ) 1
b
r r
2 b′r − b
b′r − b
Φ′
p r = 1 − Φ′ + (Φ′)
8πG r
− Φ′ − +
2r(r − b) 2r 2 (r − b)
r + Λ , (12)
where
ρ (r)
is the energy density,
τ (r)
is the radial tension,
p(r)
is the pressure measured in the lateral
directions, orthonormal to the radial direction.
We obtain the equation for τ ′ by taking the derivative of Eq. (11) with respect to the radial coordinate r
and eliminating b′ and Φ′ , given in Eqs. (10) and (12), respectively,
![]()
τ ′ = (ρc2 − τ )Φ′ − 2 (ρ + τ ). (13)
r
Equation (13) is known as the relativistic Euler equation or the hydrostatic equilibrium equation for the material
threading the wormhole. This equation can also be obtained using the conservation of the stress-energy tensor
;
T µˆνˆ =
0 , putting
µ′ = r . The conservation of the stress-energy tensor can also be deduced from the Bianchi
;νˆ
identities, which are equivalent to Gµˆνˆ = 0 .
EXTERIOR SOLUTION WITH GENERIC Λext
The exterior vacuum solution of Einstein field equations is given by
ds2 = −−
ext
GM
dt 2 + −
ext
Λ | r 2 + 1 − | 2 | Λ | r 2 + 1 − | GM | | |||
3 | | r | | 3 | | r | | ||
1
2
−
dr 2 + r 2 (dθ 2 + sin2 θdϕ 2 )
(14)
where
0 ≤ r < ∞ . This is the solution of de-Sitter black hole with a conformally coupled scalar field and also
known as MTZ solution. The scalar field is given by
φ(r) =
3 GM
![]()
4π r − GM
. (15)
![]()
The MTZ solution exists only for a dimensionless constant, α = − 2 πΛG , and describe a static and
9
spherically symmetric black hole with a positive cosmological constant Λ. The mass of the black hole satisfies
0 > GM > l / 4 , where l is the cosmological radius and is given by l =
cosmological horizon satisfies 0 < r− < GM < r+ < l / 2 < rc < l , where
![]()
3/ Λext . The inner, event and
![]()
r = l (−1+
− 2
![]()
![]()
r = l (1−
+ 2
![]()
![]()
r = l (1+
![]()
1+ 4GM / l ), (16)
1− 4GM / l ), (17)
1− 4GM / l ). (18)
++ 2
The solution (14) have singularities at the radii
![]()
r = l (±1
± 2
![]()
1− 4GM / l ).
r = r+
= rb
can be
considered as the event horizon of the vacuum black hole solution, but since the wormhole matter will fill region up
to a wormhole radius a superior than rb . This radius does not enter into the problem. For the same reason, r = r− ,
the inner event horizon of the black hole is not considered in the present problem. So r = r++ = rc
can be regarded
as the position of the cosmological event horizon of the de-Sitter spacetime. Keeping Λext fixed, if one increases M,
−1
r = r+
will increase and r = r++
will decrease. For the maximum allowed value of the mass, M = l(4G)
, the
black hole event horizon and cosmological horizon are same i.e.,
r+ = r++ = l / 2 . In the case of vanishing
cosmological constant Λext = 0, the geometry of the extreme Reissner-Nordström metric
2
ds2 = −1 − GM
−2
dt 2 + 1 − GM
dr 2 + r 2 (dθ 2 + sin 2 θ dφ 2 ), (19)
![]()
r
![]()
r
which has coalesced inner and event horizons at
r+ = r− = GM . For the massless case,
M = 0 , the black hole
geometry in de-Sitter spacetime and the metric takes a simple form
![]()
−
ds2 = 1− Λ
dt +
ext r 2 2
dr 2
![]()
+ r 2 (dθ 2 + sin 2 θ dφ 2 ). (20)
− Λ
3
1 ext r 2
3
For Λext → 0 , the de-Sitter metric tends to the Minkowskian spacetime.
JUNCTION CONDITIONS
In order to match the interior and exterior matrices, one needs the boundary surface S that connects them.
The first condition is that the metric must be continuous at S , i.e.,
g
int
µν
![]()
![]()
= g
ext
S µν
S . This condition is not sufficient
to join different spacetimes. The second condition for making the match can be done directly with the field equation, due to the spherically symmetric. We can use the Einstein field equations, Eqs. (7), (8) and (9), to determine the energy density and stresses of the surface necessary to have a match between the interior and exterior solutions. When there is null stress-energy terms at S, we can say that the junction is a boundary surface. On the other hand, if surface stress-energy terms are present, the junction is called the thin-shell.
Since both the inside and outside matrices are spherically symmetric, the components Gθθ
and Gφφ
are
already continuous, and therefore one is left with imposing the continuity
Gtt
and
Grr , these can be written as
![]()
g
int
tt
![]()
= g
ext
r =a tt
r =a
![]()
rr
and g int
![]()
= g
ext
r =a rr
r =a . At r = a , with
g
int
tt
rr
and g int
being the metric components for the
interior region at r = a , and g ext and g ext
the exterior metric components for the vacuum solution at r = a . We
tt rr
are considering the interior solution Eq. (1) and the MTZ exterior solution Eq. (14) matched at surface, S. The continuity of the matrices then give generically Φint (a) = Φext (a) and bint (a) = bext (a) . Now comparing Eqs.
and (14), the red shift and shape functions can be written as
2
Φ(a) = 1 ln− Λext a2 + 1− GM
, (21)
![]()
![]()
![]()
2 3
2 2
a
![]()
b(a) = 2GM − G M
a
![]()
+ Λext a3 . (22)
3
We consider a particular choice in which the static interior observer measures zero tidal forces, i.e., Φint = const.
and
Φ′int = 0 . Since the shell is infinitesimally thin in the radial direction, so there is no radial surface pressure.
Therefore we are left with a surface energy density σ and a surface tangential pressure P .
At the boundary S , the stress-energy tensor Tµˆνˆ is proportional to a Dirac delta function, so one can write
Tµˆνˆ = tµˆνˆ δ (rˆ − aˆ). To find tµˆνˆ we then use
+
+
−
∫ Gµˆνˆ drˆ = 8πG∫tµˆνˆδ (rˆ − aˆ)drˆ , (23)
+
where ∫
−
−
means an infinitesimal integral through the shell. Now using the property of the δ function
+
![]()
δ ( f (x)) = [1/ f ′(x) ]δ (x), and
∫ g(x)δ (x − x0
−
) = g(x0
), we find
1 +
![]()
−
tµˆνˆ = 8πG ∫Gµˆνˆ drˆ . (24)
b′
We see that
![]()
Gtˆtˆ = r 2
only depends on the first derivative of the metric, which are continuous for interior and
exterior solutions. Thus, since the integral gives the value of the metric on the exterior side (b+ , say)
value of the metric on the interior side (b− , say) , it gives zero, and one finds σ = 0 .
minus the
In Eq. (9) we see that
Gθˆθˆ has an important term
[1 − (b / r )]Φ′ , the other terms in this equation
depend at most on the first derivative and do not contribute to the integral. From Eq. (23), we obtain
8πG / p =
![]()
−
1 − b(a)/ a Φ+ . Now
Φ
−
+ = 0
is taken before and
GM
Φ + =
G 2 M 2
−
![]()
3
− Λ ext a
![]()
(1 − b(a)/ a). Therefore, the surface tangential pressure can be
![]()
![]()
a
a
2 3
obtained as
2 2
GM − G M − Λext a2
![]()
![]()
![]()
P = 1 a
8πGa
a2 3
1 − b(a)/ a
. (25)
This equation can be written more explicitly as
2 2
![]()
GM − G M − Λ ext a 2
![]()
P = 1
8πGa
![]()
![]()

a
1 −
a 2
2
GM
3
− Λ ext r 2
. (26)
a 3
One can obtain the matching equation of the radial pressure across the junction boundary of the thin-shell. This is done by considering two general solutions of Eq. (1), and an interior and exterior solutions matched at the junction surface. The radial component of the Einstein Eq. (11), provides us
bint
![]()
= 8π G τ
(r) + Λ
+ 21 − bint Φ′int ,
(27)
r 3 int
int
![]()
![]()
r r
![]()
bext
= 8π G τ
(r) + Λ
+ 21 −
bext Φ′ext
![]()
![]()
.
(28)
r 3 ext
ext
r r
At the junction boundary, one has obtained
Φint (a) = Φ ext (a)
and
bint (a) = bext (a) . For simplicity, we are
considering Φ′int (a) = 0 . From Eq. (21) we have
GM
G2 M 2 Λ
![]()
2
−
![]()
Φ′(r ) = r
![]()
![]()
− ext
r3 3
2
r
. (29)
− GM
Λext 2
1
![]()
− r
r 3
Using Eqs. (29) and (26), we verify that Eqs. (27) and (28) provide us with an equation which governs the behavior of the radial tension at the boundary, namely
τ int
(a) +
1
![]()
8π G
Λint
= τ ext
(a) +
1
![]()
8π G
Λ ext
![]()
+ 2 PeΦ (a) , (30)
a
where we have put eΦ (a) =
2
1 − GM
− Λext a2
. This equation relates the radial tension at the surface with
![]()
![]()
![]()
a 3
the tangential pressure of the thin-shell.