International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 338
ISSN 2229-5518
Geometrical modeling of a composite folded membrane by a developable membrane with parabolic guidelines of any order
E.T. Olodo, E.C. Adjovi , S.N. Krivoshapko
—————————— ——————————
The twisted membranes belong to the family of developable surfaces whose principal advantage as one knows it resides in their capacity to be spread on a plan without distortion lengths, tearing and crumpling. The applications of developable surfaces in industrial circle are varied. Indeed, the structures whose surface is developable are simply manufactured by folding of their developed form, cut out in a sheet of material. This process is used for example in shipbuilding for the manufacture of the hulls of boat [1]. In the field of the civil engineering and architecture, developable surfaces are generally regarded as a technical method for realization of complex forms. However, the study suggested in [2] show that they can be used like aesthetic tools with whole share.
The current evolution of technology brings to carry out increasingly complex projects, expensive and subjected to increasingly severe constraints of safety. The thin hull belongs to the family of structural surfaces which includes the membranes, folded surfaces and hulls. The hulls with simple or S curve are of everyday usage in structural engineering (engineering mechanical, civil, shipbuilding, aeronautical, etc).Vis-a-vis the geometrical complication of the majority of the structures membrane, the recourse to models more innovating, robust and fulfilling the requirements of reliable simulation as well as possible, proves to be paramount. The recourse to the material concrete to build 3D surfaces a little lost today with the profit of other materials the such composites. In addition, a complete modeling 3D with voluminal finite elements causes costs of prohibitory calculations as well as numerical problems of blockings for the mean structures.
An alternative resides in the development of a macroscopic model which consists in replacing a
developable composite membrane by a system of plane quadrilateral elements i.e. a curved membrane by a folded surface. This approach is justified especially for developable surfaces bus by definition they are made of a mono parametric family of tangent plans on these surfaces according to the right generatrixes.
In this work, one proposes a macroscopic model allowing the simulation of working of a composite on a macroscopic scale by using a geometrical modeling much simpler than those of the literature like that proposed in [3].This model suggested is based on a method of approximation of a composite folded membrane by a twisted surface with parabolic guidelines of any order.
The modeling of developable surfaces is a complicated problem, especially if one does not force the
surface to be regular of class ∁². Developable surfaces are
isometric surfaces in the plan. The theorem of Minding
states that two surfaces having even constant Gaussian curve are isometric. In this case, the theorem egregium indicates that the curve of Gauss of a developable surface is inevitably null in any point.
In general, it is more convenient to define a developable surface by a vector equation set of the shape:
r⃗ = r⃗ (u ,v) = x (u ,v) ⃗ +y(u ,v)/⃗+z(u ,v)k-⃗, (1)
or by parameterized form: x=x(u,v), y=y(u,v), z=z(u,v) which
may be one of the types:
z = z (u , v), (2) M(x, y, z) =0, (3)
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 339
ISSN 2229-5518
The expression (2) defines the coordinate z as a direct parameterization and (3) as a dual parameterization where not all the plans are parallel and the family of plans does not form a beam, that is, there is not a right common to
all these plans.
construction of its developed and that of the folded surface built starting from twisted surface [11].
For considered twisted surface, when m=n, we obtain the equation of the cusp edge in the form:
Discretization: There is not discrete equivalent of the Gaussian curve, several expressions were proposed besides “[4],[6]”. Consequently, there is not single solution to
discretize a developable surface. The method described in [7]
z 0,
y 0,
![]()
x l ,
(1 n1 a b )
for example is based on the representation of tangent developable surfaces. The cuspidal edge is discretized and
becomes a polygon.
I.e. we have a cone if a≠b or a cylinder if a=b.
When m ≠ n, we obtain the equation of the cuspidal edge by the resolution of the following system:
Another solution consists in defining a developable surface as a surface being able to be put flat without being stretched. While following this step, the models of the type
M 0,
![]()
M 0,
2 M
![]()
2
0 ,
“band” were proposed. They consist of an articulated assembly of plane elementary forms forming a band. In [8],
For example for m=2, n=4 we find:
the elementary forms are triangles. It is then possible to obtain developable approximations of surfaces which are not it. Same manner one can choose plane quadrilaterals to compose a band. This process is used for example in [9].![]()
x bl ,
b 6a 2
y
2a² 6
![]()
,
b 6a ²
z
4a 3
![]()
b 6a ²
. (7)
Limiting surface obtained is then developable.
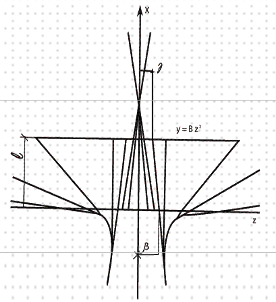
Let us consider a twisted surface whose curved generatrixes are plane parabolas of order m and n:
Let’s assume that: a=0.5; b=1; l=5; m=2; n=4. The formula
(2) will take the following form:
M (2 6 3 4 ) x 10 y 20 3 z 15 4 0 ,
and of (6) we will have 3 .
(8)
x 0 ,
y a z n
and
x l ,
y bzm .
(4)
The twisted surface with parabolic guidelines of
In this case, the parametric mono equation of the family of the plans will have the following form:
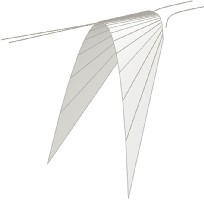
order m=2, n=4 and its corresponding cuspidal edge are shown in fig.1a and fig. 1b. From (7) one can determine the coordinates of the remarkable point for (not of![]()
M (n1)(l x)n nn1(x zl) 1 (lybx m) 0, (5)
a
return): 0,
x l,
y z 0;
![]()
for b 6a
Where β=z, parameter of the parabola of the plan x=0 and y=z, parameter of the other parabola. The parameters β and γ are bound by the following relation [10]:
an n1
there is a rupture of the cuspidal edge.
y bz 2
y az 4
![]()
m 1
bm
![]()
. (6)
By introducing (6) into (5) we will have:
M M ( x, y, z, ) 0.
The right generatrix of the twist passes by the point β=z of parabola of order n and by the corresponding point γ =z of parabola of order m.
A twisted surface is completely given by its cuspidal edge whose definition is sufficient for the
Fig. 1a.Twisted surface with parabolic guidelines
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 340
ISSN 2229-5518
M ( 0.5) 0.15625x 10 y 2.5z 0.9375 0,
M ( 1) x 10 y 20z 15 0,
x 5,
B (x, y, z) = B (5; 0.12 ; 0.56)
M ( 1) x 10 y 20z 15 0,
M ( 1.5) 7.59 x 10 y 67.5 z 75.94 0,
x 0,
C (0 ; 1.04 ; 1.28)
C(x, y, z)
M( 1) 0; M( 1.5) 0;
x 5,
C (5;3.32; 2.18).
Fig. 1b.Surface with corresponding cuspidal edge
The algorithm of construction of the folded surface on the basis of given twisted surface is studied in [12]. Let us build the developed of the folded surface (fig. 2), tangent to the given twist according to the right generatrix when
0; 0.5; 1; 1.5.
We obtain the coordinates of the angular points of the folded surface as being the components of the points of intersection of three plans. Two plans will be given by two sides close to the folded surface which one can obtain by the mono parametric equation of the family
of the plans (5) by fixing two parameters .The third
plan will be that to which belongs the corresponding curved guideline of the twist, for example the plan x=0 or the plan x=l=5. So, we shall have:
M ( 0) 10 y 0,
M ( 0.5) 0.15625x 10 y 2.5 z 0.9375 0,
x 0,
A(x, y, z)=A(0 ; 0 ; 0.375),
M ( 0) 10 y 0,
M ( 0.5) 0.15625x 10 y 2.5 z 0.9375 0,
x 5,
A (x, y, z) = A (5 ; 0 ; 0.062),
M ( 0.5) 0.15625x 10 y 2.5 z 0.9375 0,
M ( 1) x 10 y 20 z 15 0,
x 0,
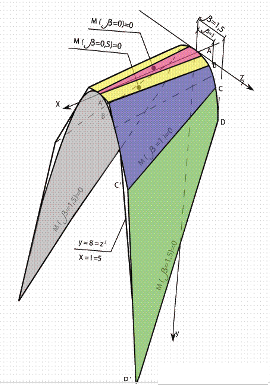
Fig. 2.Folded surface obtained from developable surface
B(x, y, z) = B (0 ; 0.107 ; 0.8)
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 341
ISSN 2229-5518
1- Developed of the twist
2- Developed of the folded surface
In fig. 2 one shows obtained folded surface. The side DD’
is formed by the right generatrix of the twist when
Let us build considered developed twist by the method suggested in [11]. Knowing that the vectorial
equation of a twisted surface is written in the following
1.5 ,
3 3.375, thus coordinates of the
form:
point D’ will be D(5; 11.39; 3.375) and those of the
point D will be D(0; 2.53; 1.5).
r (u, ) xi yj zk u
xi yj z k
![]()
, with
Having determined the coordinates of the
x² y ² z²
angular points of folded surface, it is easy to calculate the linear and angular values necessary to construction of developed folded surface (fig. 3).
x x( ) , y y ), z z ( ) - parametric equation of the
cuspidal edge (4) and u, - curvilinear coordinates of the twist, ![]() u
u![]() -the distance between the cuspidal edge and any point parallel to taken the tangent with the cuspidal edge, we
-the distance between the cuspidal edge and any point parallel to taken the tangent with the cuspidal edge, we
obtain the equations of the guideline parabolas: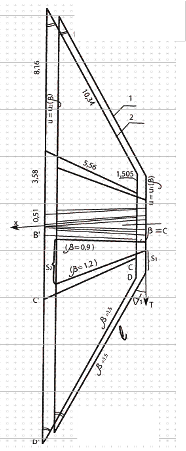
u1
![]()
1
b 6a ²
b²l ² (ab 4 4a² 6 )² (b 2a 3 )² ,
u2
1
![]()
b 6a ²
36a²l ² 4 (6a² 6 24a b
3 )² (6a 3 12a² )²
b
Where u1 u1 ( ) -equation of the parabola of order n=4,
u 2 u2 ( ) - equation of the parabola of order m=2.
The length of the right generatrix between the guideline parabolas is determined by the following formula:
t u2 u1 .
The angle formed by the parabola and the right generator can be calculated by the following formula:
cos i
![]()
F ui
u ² 2Fu B 2 12 with i=1;2.
i i i
The lengths of the extreme curves between the corresponding right generators are determined by the![]()
2
formula: Si
1
u ² 2Fu B 2 d ,
with i= 1 ; 2. In the
two last formulas expressions![]()
![]()
F ru r ,
![]()
![]()
B² r r
[11]
Fig. 3.Developed folded surface
are the coefficients of the first quadratic form of a surface.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 342
ISSN 2229-5518
The subscripts of B indicate that these coefficients must be taken with u ui (I=1 ; 2).
Let us build developed twisted surface for which the mono parametric equation of the family of the plans is obtained in the form (8). The values of t, αi, Si will be given in the interval 0≤β≤1.5 with spacing ∆β=0.3. It is easy to execute these calculations on computer. The
results of calculations are reported to table 1.
Developed twisted surface is shown in figure 3.One can notice that for the determination lengths of the extreme curves between the corresponding right generatrixes, one uses the following formula of analytical geometry [13]:![]()
z z
membranes’ modeling is a complicated problem and sometimes inextricable therefore that it does not impose on the surface to be of certain regularity. So, the possibility of the replacement of a developable composite surface by a folded surface lets you extend the fields of application of these membranes because with the increase in the number of edges (boundaries), one could get a folded structure identical to the expandable membrane of reference. This offers new perspectives to the design of a new variety of folded composite structures.
The theory concerning working of the composite structures with developable form was the subject of a number of studies for example in [14]. In a general way, concerning the composites, for the production of
developable forms one often uses thermohardening resins
S
z
1 ( dy )² dz ,
dz
whose reinforcements are presented in the form of continuous chechmates i.e. distributed tablecloths in a
one-way way. Indeed, the composite membrane object of
For our case where n=4, m=2 (see formula (4)), it takes the
form:![]()
z1 z1
our study is reinforced resin polyester with one-way fiberglass bus today, only the macroscopic approaches make it possible to simulate working of the composite
S1
z
![]()
z
1 16a² z 6
dz ,
1
z1 , (n 4)
![]()
![]()
1
z2 z2
membranes of this class. The lower scale models make it
possible as for them studied the behavior of a reinforcement starting from the assembly of its elementary components. However, the macroscopic scale
S 2
1 4b² z²
2
(m=2).![]()
8b²
ln z
2b
1 4b² z ²
z2
considers the reinforcement as a continuous material
whose behavior is closely related to its internal structure but this one does not appear in an explicit way in
modeling. The majority of the digital simulations on this
TABLE 1
1 2 1
scale use a continue approach “[15],[16]”.
2
In this work we can retain the following:
It’s proceeded to the study of developable composite membrane with parabolic guidelines as two plan parables of order m and n: x=0, y=azn and x=l, y=bzm. This developable membrane, it is established the mono parametric equation of family plans and the equation of the cuspidal edge. The cuspidal edge of the developable surface with parabolic guidelines of order n=4, m=2![]()
presents a singular point (x=l, y=z=0).When z=.Jb/6a , it
has a break from the cuspidal edge.
It is built the developed of the folded membrane tangent to the developable membrane following four
straight generatrixes (fig. 2; fig. 3).
The results obtained show that the method of approximation proposed as part of this work can be used to get a complete and relevant solution with a time of calculation on computer, by far much lower than the
finite element method. Developable composite
A method for the construction of the developed of the twisted membrane is developed. Through this approach, we see that with the increase in the number of edges of the folded surface, the dimensions of its developed approximately are very close to those of the corresponding developable membrane. This offers a considerable interest of practical application for the
formatting of folded composite membranes.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 343
ISSN 2229-5518
[1] C. Chu and J.T. Chen, “Characterizing degrees of freedom for geometric design of developable composite Bezier surfaces,” Rob. and Computer- Integr. Manuf., vol. 23, pp. 116-125, 2007.
[2] G. Glaser, and F. Gruber,”Developable surfaces in contemporary architecture,” J. Math. and the Arts, vol. 01, pp.59-71, 2007.
[3] G. Hivet and P. Boisse, “Consistent 3Dgeometrical model of fabric elementary cell. Application to a meshing preprocessor for 3D finite element analysis,” Finite Element in Analysis and Design, vol.
42, n°1, pp.25-4, 2005.
[4] J.M. Sullivan, “Curvatures of smooth and discrete surfaces,” Springer, Discrete Differential Geometry, vol.
38, pp.175-188, 2008.
[5] C. Wang and K. Tang, “Achieving develop ability of polygonal surface by minimum deformation: a study of global and local optimization approaches,” The visual computer. Int. J. Comp. Graph., vol. 20, pp.521-539, 2004.
[6] H. Yamauchi, S. Gumhold, R. Zayer and H.P. Seidel, “Mesh segmentation driven by Gaussian curvature,” Visual Computer, vol. 21, pp.649-658, 2005.
[7] H. Pottmann and J.Wallner,”Computational line
Geometry,” Springer, ISBN 3-540-42058-4, pp.565,
2001.
[8] C. Wang and K. Tang, “Developable triangulations of strip,” Computer-Aid Design & App., vol. 2, pp.233-
242, 2005.
[9] Y. Liu, H. Pottmann, J.Wallner,Y.L. Yang and W.
Wang, “Geometric modeling with conical meshes and developable surfaces,” ACM Trans. Graph., vol.
25, pp.681-689, 2006.
[10] S.N. Krivoshapko, “Construction, calculation and application of the developed membranes in the thin- walled structures,” Calculation of the thin walled
structures, Edns. Russian Friendship University, pp.54-
66, 1982. (in Russian)
[11] S.N. Krivoshapko, “The application of developable surfaces in shipbuilding,” Shipbuilding, vol. 7, pp.5-7,
1983. (in Russian)
[12] S.N. Krivoshapko, A.G. Shtykov and V.P.
Shabanov, “Replacement of the twisted membranes by plane elements,” Bul. Mil. Eng., vol. 2, pp. 18-21,
1982.. (in Russian)
[13] G.C. Badjoria, “On a method of construction of the developed of a twisted surface,” Shipbuilding, vol. 9, pp. 37-38, 1984. (in Russian)
[14] A. Cheruet, ‘’Analyse et simulation de la mise en forme de composites
thermodurcissables,’’ Thèse de doctorat
Université d’Orléans, 2001.
[15] X.Q. Peng, J. Cao, “A continuum mechanics- based non orthogonal constitutive model for
woven composite fabrics,” Composites Part A, vol.
36, n°6, pp.859-874, 2005.
[16] R.H.W. Thije Ten., R. Akkerman and J. Huétink, “Large deformation simulation of anisotropic material using an update Lagrangian finite element method,” Computer Method in Applied
Mechanics and Engineering, vol. 196, n°33-34,
pp.3141-3150, 2007.
Author details:
E.T Olodo : Ecole Polytechnique d’Abomey-Calavi
(EPAC)/Université d’Abomey-Calavi (UAC), Benin
03BP1409 Cotonou, E-mail : olodoe@live.fr
E.C. Adjovi : Ecole Polytechnique d’Abomey-Calavi (EPAC)/Université d’Abomey-Calavi (UAC), Benin O1 BP 2009 Cotonou, E-mail : adjed2012@gmail.com
S.N. Krivoshapko: Peoples’ Friendship University of Russia,
6, Miklukho-Maklaya Str., 117198, Moscow,Russia
IJSER © 2013 http://www.ijser.org