International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 1

ISSN 2229-5518

Furtherance of Elliptic Curve Cryptography Algorithm in the field of GSM security Satarupa Chakraborty

Abstract-- Mobile Phones have totally changed the world; nowadays people can afford to forget their daily household needs but not their own mobile phones. This increasing popularity has sensed a huge growth in the acceptance of modern mobile phones. With the increasing number of features in mobile phones security has become the chief area of concern as it is apposite to all the authoritative applications throughout the world. Today as GSM accounts for 80% of the total mobile phone technologies in the market so lack of security measures can crumple resulting in hampering of its service. Some of these security issues have been sort out using 3GPP. In this pa per we will be centralizing our discussion on the operational methodology of RSA algorithm and elliptic curve cryptography algorithm and will be closely examining which of the above anticipates a secure method of encryption for GSM key generation.

Index Terms-- elliptic curve cryptography, RSA, GSM, security, cryptography, finite field, discrete logarithmic problem

——————————  ——————————
‘burst period’ and it lasts 15/26 ms (or approx. 0.577 ms).

1 INTODUCTION

The last few years have witnessed an unprecedented emergence in the wireless industry. The ever increasing demands of users have triggered an increasing involvement among researchers and industries to come up with a comprehensive manifestation for more upgraded mobile communication systems. Mobile phones are being used on daily basis by millions of users so privacy of user’s phone calls and text messages (data) need to be ensured and unauthorized use of the service needs to be prevented. It is highly mandatory to take sensible technological security measures. The risk of encroachment and eavesdropping has been increasing with gadgets becoming wireless and ubiquitous. As such it gives rise to an alarming issue with spectra of hackers/crackers bulking large [1] [2].The successful deployment of GSM over the last two to three decades has been noteworthy as it has been to corroborate most of world’s mobile phone networks. GSM has been dubbed the “Wireless Revolution” and it doesn’t take much to realize why. GSM provides a secure and confidential method of communication. Most GSM systems operate in the 900 MHz and 1.8 GHz frequency bands.GSM divides up the radio spectrum bandwidth by using a combination of Time- and Frequency Division Multiple Access (TDMA/FDMA) schemes on its 25 MHz wide frequency spectrum, dividing it into 124 carrier frequencies (spaced
200 KHz apart). Each frequency is then divided into eight
time slots using TDMA, and one or more carrier frequencies are assigned to each base station. The fundamental unit of time in this TDMA scheme is called a

————————————————

 Satarupa Chakraborty has completed her master’s degree (M.TECH) in computer science and engineering from Institute of Engineering and Management, India, E-mail: satarupa85@gmail.com

Therefore the eight ‘time slots’ are actually ‘burst periods’, which are grouped into a TDMA frame, which subsequently form the basic unit for the definition of logical channels. One physical channel is one burst period per TDMA frame [3]. GSM was designed to grow and meet the needs of new technologies. GSM is currently composed of GPRS, 3G, and EDGE. EDGE is a technology that allows improved data transmission rates as a backward compatible extension of GSM. GPSR is designed for web- browsing. 3GSM is the GSM running on third generation standards for multimedia services [4]. It allows full roaming from operator to operator if mutual bilateral agreements are in place [5]. For security of the transmit ion of sensitive information cryptography and security authentication protocols were devised to ensure confidentiality, authentication and integrity of communications. Security protocols like SSL [6] and SET [7] already exist. Encryption can be broadly categorized into two forms: Symmetric and asymmetric encryption techniques. Most of symmetric encryption is based on RSA public key cryptography. But asymmetric key cryptography using elliptic curve cryptography (ECC) is designed which has been able to maintain the security level set by other protocols [8].
In this paper Section 2 discusses about the importance of GSM and the requirements of GSM security. Section 3 discusses about RSA algorithm. Section 4 overview about ECC while 5 discusses its implementations. Section 6 discusses about the comparison of RSA and ECC.

2 GSM AND ITS SECURITY

GSM technology was introduced in the early 1980s by the European Telecommunications Standards Institute (ETSI). Global System for Mobile communications or GSM uses digital modulation to improve voice quality but the network offers limited data service. As demand drove

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 2

ISSN 2229-5518

uptake of cell phones, GSM continued to improve
transmission quality and coverage. GSM carriers also began
to offer additional services, such as paging, faxes, text messages and voicemail. Developed as a replacement for first generation (1G) analog cellular networks, the GSM standard originally described a digital, circuit switched network optimized for full duplex voice telephony. The standard was expanded over time to include first circuit switched data transport, then packet data transport via GPRS (General Packet Radio Services). Packet data transmission speeds were later increased via EDGE (Enhanced Data rates for GSM Evolution) referred as EGPRS. The GSM standard is more improved after the development of third generation (3G) UMTS standard developed by the 3GPP. GSM networks will evolve further as they begin to incorporate fourth generation (4G) LTE Advanced standards. GSM was designed to grow and meet the needs of new technologies.
The main advantages of GSM are:
1) Better voice quality and low-cost alternatives to making calls.
2) Ease for the network operators in deploying equipment from any vendors that implement the standard.
3) GSM allows network operators to offer roaming services so that subscribers can use their phones on GSM networks all over the world.
4) Delivering mobile data.
5) Offering greater network capacity.
6) Operating with existing second-generation technologies.
7) Enabling rich data applications such as VoIP, video telephony, mobile multimedia, interactive gaming and more.
Though GSM faces the disadvantages of having bandwidth limitations as multiple users uses the same bandwidth and it even causes electronic interference.
GSM was designed with security in mind. Older cellular systems were analog based and therefore very susceptible to security attacks. It was common for attackers to eavesdrop and intercept people’s conversations and data. Even worse yet, attackers were capable of stealing customer IDs to make fraudulent calls. GSM also beats out its competition by providing authentication, secure data transfer, and subscriber data transfer. GSM has many benefits over its predecessors in terms of security, capacity, clarity, and area coverage. A GSM network is composed of several functional entities, whose functions and interfaces are specified. Figure 1 shows the layout of a generic GSM network. The GSM network can be divided into three broad parts. The Mobile Station is carried by the subscriber. The
Base Station Subsystem controls the radio link with the
Mobile Station. The Network Subsystem, the main part of
which is the Mobile services Switching Center (MSC), performs the switching of calls between the mobile users, and between mobile and fixed network users. The MSC also handles the mobility management operations. Not shown is the Operations and Maintenance Center, which oversees the proper operation and setup of the network. The Mobile Station and the Base Station Subsystem communicate across the Um interface (represents the radio link), also known as the air interface or radio link. The Base Station Subsystem communicates with the Mobile services Switching Center across the A interface [9].

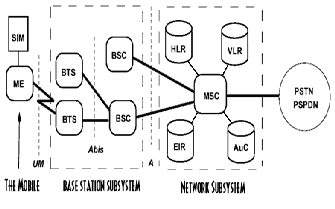
Figure 1: GSM architecture
The best way to appreciate security is by looking at how chaotic and dangerous a mobile communication system would be without security. At any given moment, anybody could eavesdrop into your conversation. Ones bank account information, daily schedule, and any other information that one may disclose on the phone would be at risk. Besides listening in, at any given moment, a hacker could impersonate user information to make calls that would later amount to thousands of dollars in service charges [4]. The security methods standardized for the GSM System make it the most secure cellular telecommunications standard currently available. Although the confidentiality of a call and anonymity of the GSM subscriber is only guaranteed on the radio channel, this is a major step in achieving end-to-end security. The subscriber’s anonymity is ensured through the use of temporary identification numbers. The confidentiality of the communication itself on the radio link is performed by the application of encryption algorithms and frequency hopping which could only be realized using digital systems and signaling. The security architecture of GSM was originally intended to provide security services such as anonymity, authentication and confidentiality of user data and signaling information [10].

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 3

ISSN 2229-5518

This substantial loss incurred by the operator due to GSM
fraud against a specific wireless carrier may include the
following:
1) Indirect financial loss resulting from decrease in the number of customers and increase in use of the system with no revenue.
2) Direct financial loss, where money is paid out to
others, such as other networks, carriers and operators of 'Value Added Networks' such as Premium Rate service lines.
3) Potential embarrassment, where customers may move to another service because of the lack of security.
Failure to meet legal and regulatory requirements, such as License conditions, Companies Acts or Data Protection Legislation. [11]
The security goals of GSM are as follows:
1) Confidentiality and Anonymity on the radio path.
2) Authentication of mobile users for the network.
3) Confidentiality of user data and signaling information even in competition pressure or accidentally.
4) Anonymity of subscriber’s identity.
5) Using SIM (Subscriber Identity Module) as a security module [10].
6) Keys are securely stored [4] [17].
GSM security design requirements must take into account environment and security measures as:
1) Must define security procedures for generation and distribution of keys.
2) Exchange information between operators.
3) Maintain confidentiality of algorithms.
4) Must be a cost effective scheme [12].
Whereas GSM security measures must not:
1) Increase the bandwidth of the channel.
2) Increase the error rate.
3) Increase error propagation.
4) Add expensive complexity to the system.
5) Increase the error rate.
6) Significantly add to the delay of initial call setup or
subsequent communication [12].
The GSM security architecture:
1) Each mobile subscriber is authenticated with a unique 128 bit secret key (Ki).
2) Ki is stored in Subscriber Identity Module (SIM)
which is inserted in the mobile phone.
3) Ki of each subscriber also gets scored in Authentication Center (AuC) associated with the HLR in the home network.
4) The SIM is designed as a tamper resistant smart
card to avoid extraction of the customer’s Ki (as if
the Ki would have been extracted then the subscription could be cloned and the subscriber’s calls could be eavesdropped and it would be impossible even for the subscriber to obtain the Ki).
The levels of GSM security: Level I:
1) The subscription is authenticated in the SIM.
2) The SIM is inserted in the phone.
3) The key of the subscriber gets stored in the AuC.
4) The owner gets authenticated and billed.
5) GSM checks for the validity of the subscription.
Level II:
1) The caller makes the call.
2) GSM identifies the location of the caller.
3) The receiver identifies the caller before accepting the call.
Level III:
1) Digital encryption is made to avoid other parties from listening to the conversation.
But practically such levels cannot be bifurcated properly due to their non-existence in vacuum.
Now for the key generation for the GSM security we consider the two algorithms: RSA algorithm and ECC algorithm.

3 OVERVIEW OF RSA ALGORITHM Cryptography not only protects data from theft or alteration but can also be used for user authentication. Within the context of any application-to-application communication some specific security requirements are authentication, privacy/confidentiality, integrity, non- repudiation. In general there are three types of cryptographic schemes typically used to accomplish these goals: secret key (or symmetric) cryptography, public-key (or asymmetric) cryptography, and hash functions. Public- key cryptography has been said to be the most significant new development in cryptography in the last 300-400 years. RSA, the first PKC implementation, has been named after the three MIT mathematicians who developed it — Ronald Rivest, Adi Shamir, and Leonard Adleman. RSA today is used in hundreds of software products and can be used for key exchange, digital signatures, or encryption of small blocks of data. RSA uses a variable size encryption block and a variable size key [13]. Public key cryptography is based on the creation of mathematical puzzles that are difficult to solve without certain knowledge about how

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 4

ISSN 2229-5518

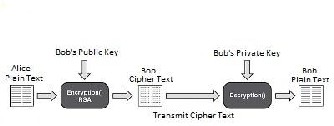
they were created. The creator keeps that knowledge secret (the private key) and publishes the puzzle (the public key). The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret [4]. Encryption and decryption are performed by identical modular exponentiation operations using a public and private key pair [10] [14]. The primary advantage of public-key cryptography is increased security and convenience: private keys never need to be transmitted or revealed to anyone. Another major advantage of public-key systems is that they can provide digital signatures that cannot be repudiated. Authentication via secret-key systems requires the sharing of some secret and sometimes requires trust of a third party as well. As a result, a sender can repudiate a previously authenticated message by claiming the shared secret was somehow compromised by one of the parties sharing the secret [15].
Figure 2: Working of RSA algorithm

3.1 The RSA algorithm [16] [17]:

The RSA algorithm uses two keys, d and e, which work in pairs, for decryption and encryption respectively.
1) Choose two distinct prime numbers, say p and q, such that p < > q.
2) Calculate n = p × q, n is used as modulus for both public and private keys.
3) Calculate ɸ (n) = (p-1) × (q-1), where ɸ (n) is Euler’s
totient function.
4) Consider an integer e, such that 1 < e < ɸ (n), so that gcd (e, ɸ (n)) = 1, i.e., e and ɸ (n) are co prime.
5) Determine d, as d × e mod ɸ (n) = 1, i.e. d is the multiplicative inverse of (e mod ɸ (n)).
6) Public Key consists of the modulus n and the
public (or encryption) exponent e, i.e., KPU = {n, e}.
7) Private Key consists of the modulus n and the private (or decryption) exponent d which must be kept secret, i.e., KPR = {d, n}.
The set: (p, q, and ɸ (n) must also be kept secret because
they can be used to calculate d.).

3.2 Encryption:

For plaintext block P < n, its cipher text C = Pe mod n

3.3 Decryption:

For cipher text block C, its plaintext is P = Cd mod n

3.4 Working Example:

1) Choose p = 17 and q = 23.
2) Calculate n = p × q = 17 * 23 = 391.
3) Calculate ɸ (n) = (p - 1) × (q - 1) = 16 * 22 = 352.
4) Choose e = 13 as e and n are co prime and
1 < e < ɸ (n).
5) Calculate d such that (d * e) mod ɸ (n) = 1.
One solution is d = 325 since [(325 × 13) % 352 = 1].
6) Public Key is (e, n) = {13, 391}.
7) Private Key is (d, n) = {325, 391}.
The encryption of plain text (P) = 127 to cipher text = C.
 Cipher text (C) = Pe mod n = 12713 mod 391 = 213. The decryption of cipher text (C) = 213 to plain text = P
 Plain text (P) = Cd mod n = 213325 mod 391 = 127.
RSA is not secure if the same message is encrypted to several receivers, to completely break RSA one needs to find the prime factors. A disadvantage of using public-key cryptography for encryption is speed. There are many secret-key encryption methods that are significantly faster than any currently available public-key encryption method. In practice, RSA has proved to be quite slow, especially for key generation algorithm. RSA is not well suited for limited environments like mobile phones and smart cards without RSA co-processors because it is hard to implement large integer modular arithmetic on such environments [18]. RSA algorithm encryption used in file encryption for small files, any file with asymmetric key encryption into its text can be more convenient to communicate and manage, and it has broad development prospects [19]. Public-key cryptography may be vulnerable to impersonation, even if users' private keys are not available. Public-key cryptography is usually not necessary in a single-user environment. For example, if you want to keep your personal files encrypted, you can do so with any secret key encryption algorithm using, say, your personal password as the secret key. In general, public-key cryptography is best suited for an open multi-user environment.

4 OVERVIEW OF ELLIPTIC CURVE

CRYPTOGRAPHY ALGORITHM

Elliptic curve cryptosystems appear to offer new opportunities for public-key cryptography. Elliptic curve cryptography relies on the believed difficulty of the elliptic curve discrete logarithm for its security. It was as an

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 5

ISSN 2229-5518

alternative mechanism for implementing public-key
cryptography designed in 1985 by N. Koblitz (University of
Washington) and V. Miller (IBM) and is becoming accepted as an alternative to cryptosystems such as RSA and ELGamal over finite fields. In public key cryptography each user or the device taking part in the communication generally have a pair of keys, a public key and a private key, and a set of operations associated with the keys to do the cryptographic operations [7] [20] [21] [22]. ECC is based on properties of a particular type of equation created from the mathematical group (a set of values for which operations can be performed on any two members of the group to produce a third member) derived from points where the line intersects the axes. Multiplying a point on the curve by a number will produce another point on the curve, but it is very difficult to find what number was used, even if you know the original point and the result. Equations based on elliptic curves have a characteristic that is very valuable for cryptography purposes: they are relatively easy to perform, and extremely difficult to reverse. Elliptic curves are also used in several integer factorization algorithms that have applications in cryptography [16]. For the purpose of cryptography, an elliptic curve can be thought of as being given by an affine equation of the form:
y2 = x3 + ax + b (1) Where, 4a3 + 27b2 ≠ 0 (2)
Where ‘a’ and ‘b’ comprises the elements of a finite field with pn elements, where p is a prime larger than 3. (The equation over binary and ternary fields looks slightly different.) The set of points on the curve is the collection of ordered pairs (x, y) with coordinates in the field and such that x and y satisfy the relation given by the equation defining the curve, plus an extra point that is said to be at infinity. The set of points on an elliptic curve with coordinates in a finite field also form a group and the operation is as follows: to add two points on the curve P and Q together, pass a straight line through them and look for the third point of intersection with the curve, R. Then reflect the point R over the x-axis to get –R, the sum of P and Q. Thus, P + Q = –R. The idea behind this group operation is that the three points P, Q, and R lie on a common straight line, and the points that form the intersection of a function with the curve are considered to add up to be zero [23]. The public key is obtained by multiplying the private key with the generator point G in the curve. The generator point G, the curve parameters ‘a’ and ‘b’, together with few more constants constitutes the domain parameter of elliptic curve cryptography [20].
The first step in setting up ECC is curve and field generation. The standard supports two types of fields:
bit length is one of eight possible values. The smallest
allowable field is of size 112 bits and the largest is of size
521 bits. The smallest field size provides a level of security comparable to a 56-bit symmetric key, while the largest field size provides a level of security comparable to a 256- bit symmetric key. When generating a field F2m the standard specifies a list of nine different fields. As before, the smallest field provides approximately 56-bit security. The largest field provides approximately 256-bit security. The list of nine possible fields was chosen so as to optimize efficiency. The listed fields have special properties that can be used to speed up ECC operations [24].
It also needs to establish the system parameters which are as follows:
 Selection of finite field and its element representation.
 Selection of elliptic curve and generator point, G,
on the curve.
 Generation of public, private key pairs consisting of a random, secret integer, k, which acts as the private key. The product of the generator point and the secret integer (k × G) acts as the primary key.
Now when after establishing the parameters if A wants send message to B then at first A chooses an elliptic curve and a point G on it which both A and B should be knowing. Then A encodes the message to be sent to the point Pm on the curve. B choose a random number (B's private key), and computes a × G (B's public key) and announces it. Then A chooses another random number k, and computes:
C = (Pm + k × (a × G), k × G). (3)
It then sends it to B. When B receives C, B computes to get Pm:
Pm = Pm – k × a × G – a × k × Q. (4)
B decodes Pm to the message. Because of the ECDLP, it is very hard for attackers to get Pm [24]. Mathematics used for elliptic curve cryptography is considerably more difficult than mathematics used for conventional cryptography resulting in its higher level of security thus making it very good for cryptographic purposes [17].

4.1 Selection of finite fields:

For performing ECC we also need to select any one suitable finite field GF (). Various finite fields admit the use of different algorithms for arithmetic. A field of a finite number of elements is denoted Fq or GF(q), where q is the number of elements. This is also known as a Galois Field. Let us consider two classes of Finite fields Fp (Prime Field, p
prime fields, denoted by Fp, and extensions of F2, denoted by F2m. When generating a field Fp one picks a prime whose
is a prime number) and

F2m (Binary finite field). The

number of elements in a finite field is always a prime or a

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 6

ISSN 2229-5518

prime power, i.e., q = p or q = pm, where the prime number
p is called the characteristic of the finite field. When q is a
prime number, i.e., q = p, the finite field GF (p) is called a prime field. The prime field GF (p) is the field of residue classes modulo p and its elements are represented by the integers in {0, 1, 2… p-1}. Following arithmetic operations defined over it:
 Addition: a, b  Fp, r  Fp, where r = (a + b) mod p
 Multiplication: a, b  Fp, s  Fp, where s = (a  b)
mod p
When q is a prime power, i.e. q = pm, the finite field GF (pm) is called an extension field. The extension field GF (pm) is generated by using an mth degree irreducible polynomial over GF (p) and it is the field of residue classes modulo the irreducible field generating polynomial. Hence, in polynomial representation the elements of GF (pm) are represented by polynomials of degree at most m - 1 with
field F , a point on that curve, P , and another point you
know to be an integer multiple of that point, Q , the
problem is to find the integer k such that k × P = Q . The problem is computationally difficult unless the curve has a “bad” number of points over the given field, where the term ``bad'' encompasses various collections of numbers of points which make the elliptic curve discrete logarithm problem breakable. For example, if the number of points on E over F is the same as the number of elements of F , then the curve is vulnerable to attack [20] [28] [29]. Hence the main operation involved in ECC is point multiplication i.e., multiplication of a scalar k with any point P on the curve to obtain another point Q on the curve.

POINT MULTIPLICATION:

Point multiplication operational deals with a point P on the elliptic curve being multiplied with a scalar number k to get another point Q on the same elliptic curve such that: k × P =
coefficients in GF (p) [26]. The finite field

F2m , called a Q.

characteristic two finite field or a binary finite field can be viewed as a vector space of m dimensions over F2, which consists of 2 elements 0 and 1. There exists m elements 0,
Point multiplication can be attained by two basic elliptic
curve operations namely:
 Point addition, which is roughly defined as addition of two point J and K to obtain another
1, 2, …, m-1 in

F2m such that each element  

F2m can

point L such that: L = J + K
be uniquely represented as

m 1

 =  a i α i , where ai  0, 1, 0  i  m.

i 0

Generally two kinds of basis are used to represent binary finite fields: polynomial basis and normal basis. Composite are binary fields of order 2m where m is a composite number. Because composite binary fields have non-trivial subfields, field arithmetic can be sped up by using lookup tables for performing subfield arithmetic. Composite binary fields are binary fields of order 2m where m is a composite number. Because composite binary fields have non-trivial subfields, field arithmetic can be sped up by using lookup tables for performing subfield arithmetic [27]. Generally two kinds of basis are used to represent binary finite fields: polynomial basis and normal basis.

4.2 Discrete Logarithm Problem (ECDLP):

The elliptic curve discrete logarithm problem is the cornerstone of much of present-day elliptic curve cryptography. It relies on the natural group law on a non- singular elliptic curve which allows one to add points on the curve together. Given an elliptic curve E over a finite
 Point doubling, which is roughly defined as addition of a point J to itself to obtain another point L such that : L = 2 × J
A small example citing point multiplication as a combination of point addition and point doubling is as follows:
Let P be a point on the elliptic curve and let k = 43 be a
scalar which is multiplied to attain another point Q on the curve by the formula Q = k × P.
As, k = 43 so, k × P = 43 × P = 2 × (2 × (2 × (2 × (2 ×P) + P)) + P)
+ P
Thus we see repetitive use of point addition and point doubling constitute the point multiplication. Other efficient methods for point multiplication are NAF (Non - Adjacent Form) and wNAF (windowed NAF) method for point multiplication [20] [28] [30].

POINT ADDITION [20] [28]:

As mentioned earlier point addition, which is roughly defined as addition of two point J and K on the elliptic curve to obtain another point L on the same elliptic curve such that: L = J + K.

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 7

ISSN 2229-5518

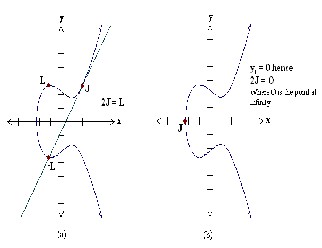
to obtain another point L on the same elliptic curve such that: L = 2 × J.
Figure 3: Point addition
 GEOMETRICAL EXPLANATION:
Take two points J and K on an elliptic curve
Two situations may occur:
1) As shown in figure (a), if we consider K ≠ -J then if we draw a line through the points J and K, it will obviously be intersecting the elliptic curve at exactly one more point -L. Now, the reflection of the point -L with respect to x-axis gives the point L, which is the result of addition of points J and K. Thus on an elliptic curve L = J + K.
2) As shown in figure (b), now if we consider
K = -J then the line drawn through this point intersect at a point at infinity O. Hence J + (-J) = O. O is the additive identity of the elliptic curve group A negative of a point is the reflection of that point with respect to x-axis
 ANALYTICAL EXPLANATION:
We start by considering two distinct points J and K such that J = (xJ, yJ) and K = (xK, yK)
Let L = J + K where L = (xL, yL), then xL = s2 - xJ - xK
yL = -yJ + s (xJ - xL)
s = (yJ - yK) / (xJ - xK), s is the slope of the line through J and
K.
If K = -J i.e. K = (xJ, -yJ) then J + K = O. where O is the point at infinity.
If K = J then J + K = 2J then point doubling equations are used.
Also J + K = K + J.

POINT DOUBLING [20] [28]:

As mentioned earlier point doubling, which is roughly defined as addition of a point J on the elliptic curve to itself
Figure 4: Point doubling
 GEOMETRICAL EXPLANATION: Take a point J on an elliptic curve.
Two situations may occur:
1) As shown in figure (a) if we double the point J to get L, i.e. to find L = 2J, then if we find that the y coordinate of the point J is not zero then the tangent line at J will intersect the elliptic curve at exactly one more point -L. The reflection of the point -L with respect to x-axis gives the point L, which is the result of doubling the point J. Thus L = 2J.
2) As shown in figure (b) if y coordinate of the point J is zero then the tangent at this point intersects at a point at infinity O. Hence 2J = O when yJ = 0.
 ANALYTICAL EXPLANATION:
We start by considering a point J such that J = (xJ, yJ), where yJ ≠ 0
Let L = 2J where L = (xL, yL), Then xL = s2 - 2xJ
yL = -yJ + s(xJ - xL)
s = (3xJ2 + a) / (2yJ), s is the tangent at point J and a is one of the parameters chosen with the elliptic curve If yJ = 0 then
2J = O, where O is the point at infinity.

4.3 Elliptic Curve Cryptography algorithm

1) Firstly we consider a curve of the form: Y2=X3+aX+b, where ‘a’ and ‘b’ constitute curve parameters.
2) Then choose a prime number.

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 8

ISSN 2229-5518

3) Computation of the points on the curve is done by implementing point adding and point doubling.
4) Selection of a generating point out of those points such that its order is large.
5) Considering a random number less than order of the generating point as a private number for each entity which acts as the secret key.
6) This entity will then generate its public key by multiplying the generating number with the secret number and will publish the point [16] [17].

5 IMPLEMENTATION OF ELLIPTIC CURVE

CRYPTOGRAPHY ALGORITHM

Interest in elliptic curve cryptosystems is fuelled by the appeal of basing a cryptosystem on a different hard problem and the fact that currently such a choice appears to lead to smaller system parameters and key sizes for the same level of security.ECC is particularly useful in applications where memory, bandwidth, and/or computational power is limited (e.g., a smartcard) and it is in this area that ECC use is expected to grow [13] [22].

5.1 Elliptic curve Diffie–Hellman (ECDH):

It is an anonymous key agreement protocol that allows two parties, each having an elliptic curve public-private key pair, to establish a shared secret over an insecure channel. This shared secret may be directly used as a key, or better yet, to derive another key which can then be used to encrypt subsequent communications using a symmetric key cipher. It is a variant of the Diffe-Hellman protocol using ECC. The Diffe-Hellman [14] [31] [32] protocol is the basic public-key cryptosystem proposed for secret key sharing.

5.2 EC Digital Signature Algorithms (ECDSA) [34]:

It is the elliptic curve analogue of the DSA. This protocol needs not only the elliptic curve operations, such as scalar multiplication, field multiplication and field inverse multiplication, but also integer multiplication, inverse operation, modular operation and a hash function [33]. As with ECC in general, the bit size of the public key believed to be needed for ECDSA is about twice the size of the security level, in bits. By comparison, at a security level of
80 bits, meaning an attacker requires about the equivalent of about 280 signature generations to find the private key, the size of a DSA public key is at least 1024 bits, whereas the size of an ECDSA public key would be 160 bits. On the other hand, the signature size is the same for both DSA and ECDSA: 4t bits, where t is the security level measured in bits, that is, about 320 bits for a security level of 80 bits.

6 COMPARISON OF RSA AND ELLIPTIC

CURVE CRYPTOGRAPHY ALGORITHM

Elliptic Curve Cryptography (ECC) is emerging as an attractive public-key cryptosystem for mobile/wireless environments. Compared to traditional cryptosystems like RSA, ECC offers equivalent security with smaller key sizes, which results in faster computations; lower power consumption, as well as memory and bandwidth savings. This is especially useful for mobile devices which are typically limited in terms of their CPU, power and network connectivity. The drawback to using ECC is that it is not as widely supported as RSA. As analyzed before, in the wireless condition, the equipment's recourse, power and compute capacity all are limited. So the encryption system in it must be low power and RAM consumption. But current the most popular algorithm RSA does not satisfy it. The elliptic curve cryptography is more effective than RSA. There are some comparisons between elliptic curve cryptography and RSA.

Table 1: The Key Size Ratio
There are a lot of differences between ECC and RSA. These differences become more and more pronounced as security levels increase (and, as a corollary, as hardware gets faster, and the recommended key sizes must be increased). A 384- bit ECC key matches a 7680-bit RSA key for security as shown in table 1. We can see the elliptic curve cryptography needs small key size but can achieve the same security level as a big key size of RSA [13] [35] [36].

Table 2: Energy cost of digital signature and key exchange computations [mJ].
Table 2 shows us the energy cost of RSA and ECDSA (a
signature algorithm of elliptic curve cryptography). From

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 9

ISSN 2229-5518

here we can clearly see that elliptic curve cryptography has
much better performance than RSA. The elliptic curve
cryptography can give a total solution for the security problems in the wireless communication, such as authentication, signature, and key exchange. The ECDSA is the elliptic curve analogue of DSA. It is a very important one of elliptic curve cryptography. The security of 322-bit ECDSA is equal to the 1024-bit RSA signature, and the length of ECDSA certification is 62 bytes, while that of RSA is 256 bytes, DSA is 168 bytes [25]. There is huge importance of shorter key lengths especially in applications having limited memory resources because shorter key length requires less memory for key storage purpose. Elliptic curve cryptosystems also require less hardware resources than conventional public-key cryptography. Now at the security level elliptic curve cryptography is more secure than RSA. RSA can be cracked successfully, uses 512 bits and for elliptic curve cryptography the number of bits is 97, respectively. It has been analyzed that the computation power required for cracking elliptic curve cryptography is approximately twice the power required for cracking RSA [28]. Elliptic curve cryptography provides higher level of security due to its complex mathematical operation. Mathematics used for elliptic curve cryptography is considerably more difficult and deeper than mathematics used for conventional cryptography. In fact this is the main reason, why elliptic curves are so good for cryptographic purposes, but it also means that in order to implement elliptic curve cryptography more understanding of mathematics is required [37].
Security is not the only attractive feature of elliptic curve cryptography. Elliptic curve cryptosystems also are more computationally efficient than the first generation public key systems, RSA and Diffe-Hellman. Although elliptic curve arithmetic is slightly more complex per bit than either RSA or DH arithmetic, the added strength per bit more than makes up for any extra computation time. The inverse operation of elliptic curve cryptography which known as the Elliptic Curve Discrete Logarithm Problem (ECDLP) gets harder, faster, against increasing key length than do the inverse operations in Diffe Hellman and RSA. As security requirements become more stringent and as processing power get cheaper and more available, elliptic curve cryptography becomes the more practical system for use. And as security requirements become more demanding, and processors become more powerful. This keeps elliptic curve cryptography implementations smaller and more efficient than other implementations. Elliptic curve cryptography can use a considerably shorter key and offer the same level of security as other asymmetric algorithms using much larger ones. Moreover, the difference between elliptic curve cryptography and its competitors in terms of key size required for a given level
of security becomes dramatically more pronounced, at
higher levels of security [17] [33].

7 CONCLUSION

This paper gives a vivid idea of GSM and its security measures. The paper also reflects on the substantiation value of elliptic curve cryptography for the possible implementation in the authentication protocol used in resource constrained mobile devices with reasonable performance compared to RSA. It gives a brief comparative study between elliptic curve cryptography and RSA. But as all the wireless communication protocols haven’t introduced elliptic curve cryptography, and as the elliptic curve cryptography’s fast hardware implementation is also being researched, the use of elliptic curve cryptography in wireless communication is more academic than in industry now.

REFERENCES

[1] REHAB EL NEMR, IMANE ALY SAROIT ISMAIL, S. H. AHMED: ACTION- TRIGGERED PUBLIC-KEY CRYPTOGRAPHY FOR GSM SYSTEMS WITH PHONE- DEPENDENT END-TO-END ENCRYPTION, VOL (5), ISSUE (2), JUNE 2006, WWW.ICGST.COM/CNIR/VOLUME5/ISSUE2/P1140626001.PDF

[2] JEREMY QUIRKE, “SECURITY IN THE GSM SYSTEM”, MAY

2004, WWW.IT.IITB.AC.IN/~KAVITA/GSM_SECURITY_PAPERS/SECU RITY IN THE GSM SYSTEM 01052004.PDF

[3] AUDREY SELIAN, LARA SRIVASTAVA: 3G MOBILE

LICENSING POLICY: FROM GSM TO IMT-2000 - A COMPARATIVE ANALYSIS.

[4] TUAN HUYNH AND HOANG NGUYEN: OVERVIEW OF GSM

AND GSM SECURITY DEPARTMENT OF ELECTRICAL ENGINEERING AND COMPUTER SCIENCE OREGON STATE UNIVERSITY JUNE 06, 2003,HTTP://WWW.D- CELL.COM/SETYOBUDIANTO/RESOURCES/GSM/OVERVIEW_ GSM_SECURITY.PDF

[5] BROOKSON, C, GSM MOU SECURITY RAPPORTEUR, BRITISH TELECOMMUN. PLC, LONDON: GSM SECURITY: A DESCRIPTION OF THE REASONS FOR SECURITY AND THE TECHNIQUES ISSUE DATE: 1994, ON PAGE(S): 2/1 - 2/4, DATE OF CURRENT VERSION: 06 AUGUST 2002

[6] THE SECURE SOCKETS LAYER (SSL) PROTOCOL VERSION 3.0, ISSN: 2070-1721, AUGUST 2011, TOOLS.IETF.ORG/HTML/RFC6101.

[7] SECURE ELECTRONIC TRANSACTION (SET) PROTOCOL, VOL.

6, WWW.ISACA.ORG/JOURNAL/PAST- ISSUES/2000/VOLUME-6/PAGES/SECURE-ELECTRONIC- TRANSACTION-SET-PROTOCOL.ASPX

[8] MRS. S. PRASANNA GANESAN: AN EFFICIENT PROTOCOL FOR RESOURCE CONSTRAINED PLATFORMS USING ECC, VOL.2 (1), 2009, PP. 89-91, WWW.ENGGJOURNALS.COM/IJCSE/DOC/IJCSE10-02-01-16.PDF

[9] HTTP://WWW.PRIVATELINE.COM/MT_GSMHISTORY/04_ARC HITECTURE_OF_THE_GSM_NETWORK/

International Journal Of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 10

ISSN 2229-5518

[10] MOHSEN TOORANI, ALI ASGHAR BEHESHTI SHIRAZI: SOLUTIONS TO THE GSM SECURITY WEAKNESSES, ISSUE DATE: 16-19 SEPT. 2008, PP. 576-581, DATE OF CURRENT VERSION: 20 JANUARY 2009, IEEEXPLORE.IEEE.ORG/STAMP/STAMP.JSP?TP=&ARNUMBER=

4756489

[11] THE GSM SECURITY TECHNICAL WHITEPAPER FOR 2002: HTTP://WWW.HACKCANADA.COM/BLACKCRAWL/CELL/GS M/GSM_SECURITY.HTML

[12] CHARLES BROOKSON: GSM (AND PCN) SECURITY AND ENCRYPTION, WWW.BROOKSON.COM/GSM/GSMDOC.PDF

[13] HTTP://WWW.GARYKESSLER.NET/LIBRARY/CRYPTO.HTML

[14] FRANCIS CROWE, ALAN DALY AND WILLIAM MARNANE: A SCALABLE DUAL MODE ARITHMETIC UNIT FOR PUBLIC KEYCRYPTOSYSTEMS, PROCEEDINGS OF THE INTERNATIONAL CONFERENCE ON INFORMATION TECHNOLOGY: CODING AND COMPUTING (ITCC’05) 0-7695-

2315-3/05, IEEEXPLORE.IEEE.ORG/STAMP/STAMP.JSP?ARNUMBER=01428

523

[15] RSA LABORATORIES: HTTP://WWW.RSA.COM/RSALABS/NODE.ASP?ID=2167

[16] VIVEK B.KUTE, P. R. PARADHI, G. R. BAMNOTE: A SOFTWARE COMPARISON OF RSA AND ECC, VOL. 2, NO. 1, MAY 2009, ISSN: 0974-1003, WWW.RESEARCHPUBLICATIONS.ORG/IJCSA/ISSUE4/2009- IJCSA-02-01-15.PDF

[17] SUKALYAN GOSWAMI, SATARUPA CHAKRABORTY, SUBARNA LAHA, ANKANA DHAR: ENHANCEMENT OF GSM SECUTITY USING ELLIPTIC CURVE CRYPTOGRAPHY, ISMS

2012, PUBLICATION YEAR: 2012, PAGE(S): 639 – 644

[18] SAMEER HASAN AL-BAKRI, M.L. MAT KIAH, A.A. ZAIDAN, B.B. ZAIDAN, GAZI MAHABUBUL ALAM: SECURING PEER- TO-PEER MOBILE COMMUNICATIONS USING PUBLIC KEY CRYPTOGRAPHY: NEW SECURITY STRATEGY, VOL.6(4), PP.

932-938, 18 FEBRUARY 2011

[19] WANG SULI, LIU GANLAI: FILE ENCRYPTION AND DECRYPTION SYSTEM BASED ON RSA ALGORITHM, ISSUE DATE: 21-23 OCT. 2011, PP. 797-800, DATE OF CURRENT VERSION: 28 NOVEMBER 2011, IEEEXPLORE.IEEE.ORG/STAMP/STAMP.JSP?TP=&ARNUMBER=

6086320

[20] ANOOP MS: ELLIPTIC CURVE CRYPTOGRAPHY, WWW.TATAELXSI.COM/WHITEPAPERS/ECC_TUT_V1_0.PDF?P DF_ID=PUBLIC_KEY_TEL.PDF

[21] THE CASE FOR ELLIPTIC CURVE CRYPTOGRAPHY-NSA/CSS,

15 JAN. 2009, WWW.NSA.GOV/BUSINESS/PROGRAMS/ELLIPTIC_CURVE.SH TML

[22] RSA LABORATORIES, OVERVIEW OF ELLIPTIC CURVE CRYPTOSYSTEMS, HTTP://WWW.RSA.COM/RSALABS/NODE.ASP?ID=2013

[23] KRISTIN LAUTER, MICROSOFT CORPORATION: THE

ADVANTAGES OF ELLIPTIC CURVE CRYPTOGRAPHY FOR WIRELESS SECURITY, HTTP://RESEARCH.MICROSOFT.COM/EN- US/UM/PEOPLE/KLAUTER/IEEEFINAL.PDF.

[24] DAN BONEH: REVIEW OF SEC1: ELLIPTIC CURVE CRYPTOGRAPHY, HTTP://WWW.SECG.ORG/COLLATERAL/SEC1REVIEW.PDF

[25] JIA XIANGYU WANG CHAO: THE APPLICATION OF ELLIPTIC CURVE CRYPTOSYSTEM IN WIRELESS COMMUNICATION,

2005 IEEE, AND

IEEEXPLORE.IEEE.ORG/STAMP/STAMP.JSP?TP=&ARNUMBER=

1618234

[26] SELCUK BAKTIR: FREQUENCY DOMAIN FINITE FIELD ARITHMETIC FOR ELLIPTIC CURVE CRYPTOGRAPHY

[27] ALFRED MENEZES: EVALUATION OF SECURITY LEVEL OF CRYPTOGRAPHY: THE ELLIPTIC CURVE DISCRETE LOGARITHM PROBLEM (ECDLP), DECEMBER 14, 2001

[28] HTTP://WWW.DKRYPT.COM/HOME/ECC#TOC-ELLIPTIC- CURVE-DOMAIN-PARAMETERS

[29] HTTP://PLANETMATH.ORG/ELLIPTICCURVEDISCRETELOGA RITHMPROBLEM.HTML

[30] DARREL HANKERSON, JULIO LOPEZ HERNANDEZ, ALFRED MENEZES, SOFTWARE IMPLEMENTATION OF ELLIPTIC CURVE CRYPTOGRAPHY OVER BINARY FIELDS, 2000, AVAILABLE AT HTTP://CITESEER.IST.PSU.EDU/HANKERSON00SOFTWARE.HT ML

[31] XU HUANG, PRITAM SHAH, AND DHARMENDRA SHARMA: FAST ALGORITHM IN ECC FOR WIRELESS SENSOR NETWORK, MARCH 17-19, 2010, PROCEEDINGS OF THE INTERNATIONAL MULTICONFERENCE OF ENGINEERS AND COMPUTER SCIENTISTS 2010 VOL II, IMECS 2010.

[32] HTTP://LIBRARY.THINKQUEST.ORG/C0126342/DH.HTM

[33] MONCEF AMARA AND AMAR SAID: ELLIPTIC CURVE CRYPTOGRAPHY AND ITS APPLICATIONS, ISSUE DATE: 9-11

MAY 2011, PP. 247-250, DATE OF CURRENT VERSION: 27 JUNE

2011

[34] DON JOHNSON AND ALFRED MENEZES AND SCOTT VANSTONE: THE ELLIPTIC CURVE DIGITAL SIGNATURE, HTTP://CS.UCSB.EDU/~KOC/CCS130H/NOTES/ECDSA- CERT.PDF

[35] ARUN KUMAR, DR. S.S. TYAGI, MANISHA RANA, NEHA AGGARWAL, PAWAN BHADANA: A COMPARATIVE STUDY OF PUBLIC KEY CRYPTOSYSTEM BASED ON ECC AND RSA, INTERNATIONAL JOURNAL ON COMPUTER SCIENCE AND ENGINEERING (IJCSE), ISSN: 0975-3397, VOL. 3 NO. 5 MAY 2011

[36] MASOOD HABIB, TAHIR MEHMOOD, FASEE ULLAH, AND MUHAMMAD IBRAHIM: PERFORMANCE OF WIMAX SECURITY ALGORITHM (THE COMPARATIVE STUDY OF RSA ENCRYPTION ALGORITHM WITH ECC ENCRYPTION ALGORITHM), 13-15TH NOV. 2009, VOL. 2, PP. 108-112, IEEEXPLORE.IEEE.ORG/STAMP/STAMP.JSP?TP=&ARNUMBER=

5360117

[37] AVANINDRA KUMAR LAL, SANDIP DUTTA: ECC BASED BIOMETRIC ENCRYPTION FOR NETWORK SECURITY, JOURNAL OF COMPUTING, VOLUME 3, ISSUE 6, JUNE 2011, ISSN 2151-9617