Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 1

ISS N 2229-5518

FPGA IMPLEMENTATIONS OF HIGH SPEED ELLIPTIC CURVE CRYPTOGRAPHY: A SURVEY

Shylashree N, Nagarjun Bhat, V Sridhar

Abs tr act:An explosive acceptance of Ellipt ic Curve Cryptography (ECC) has been attained in the industry and academics. Ellipt ic Curve cryptography is an approach to public -key cryptography based on the algebraic structure of elliptic curves over f inite f ields. The ECC is advantageous due to the provision of high level of security and the usage of small keys. In the f ield of Mobile, Wireless and Netw ork servers, to sustain the high throughput the imple mentations of high speed crypto-systems are needed. ECC has been extensively used f or hardw are imple mentation of FPGA and DedicatedASIC. Th is paper attempts to conduct a detailed survey on diff erent techniques f or imp lement ing FPGA using ECC to achieve high speed and f lexibility.

Ke ywords :ECC; FPGA; SKC; P KC; NIST ; NAF; Efficiency -Flexibility Tradeoffs; High Speed Hardware Implement at ion

——————————  ——————————

1. INTRODUCTION

Today Internet is inseparable part of our life and millions of people are using the Internet. Similarly, today there is proliferation of wireless networks based on technologies

such as Wi-Fi, Blue tooth, Wi-Max etc. unfortunately, the data going across the internet or via wireless media is not secure since their openness makes it relatively easy for intended attackers to spy on legitimate users and steal or modify the information. Hence, it is very essential to protect the information from eavesdroppers and hackers using Cryptographic techniques.
This paper is organized as follows: Section 2 gives a general
introduction to cryptography. Section 3 explains the Elliptic
curve system. Section 4 deals with the existing multiplication algorithms used in ECC. Section 5 presents a Choice of Coordinates; Section 6 reviews the related works on FPGA. Section 7 discusses the performancesummary and the conclusions arrived at, in Section 8.

2. CRYPTOGRAP HY

Cryptography is the science of using mathematics to encrypt and decrypt data. Which aims to provide some or all of the services known as Confidentiality, Integrity, and Availability: an additional Objective is Non -Repudiation[1].

2.1 Classi fication of Algorithm s in term s of Key

There are several ways of classifying cryptographic algorithms. They will be categorized based on the number of keys that are employed for encryption and decryption, and further defined by their application and use. The two types of algorithms that will be discussed are:

Symmetric Key Cryptography (SKC): Uses a single key for both encryption and decryption

Public Key Cryptography (PKC): Uses one key for encryption and another for decryption

Typically, several secret-key or symmetric Key algorithms pertaining to the class of block ciphers are used to encrypt one block of data at a time. Block ciphers ( like Twofish, Serpent, AES (Rijndael), Blowfish, CAST5, IDEA. DES, and TripleDES) transform an input block of n bits into an output block of n encrypted bits. Today, key lengths of about 128 bits and block lengths of 128 bits typically provide good security.
On the other hand, some functions such as Authentication
using digital signatures need Public-key encryption systems which use a private key that must be kept secret from unauthorized users and a public key that can be made public to anyone. The public key and the private key are mathematically linked; data encrypted with the public key can be decrypted only with the private key, and data signed with the private key can be verified only with the public key. The public key can be made available to anyone; it is used for encrypting data to be sent to the holder of the private key. Both keys are unique to the communication session. Public-key cryptographic algorithms are also known as asymmetric algorithms because one key is required to encrypt data while another is required to decrypt data.
Some examples of popular asymmetric algorithms include
RSA (Rivest-Shamir-Adleman) and elliptic curve based (ECC) cryptosystems. As far as the speed is concerned, asymmetric key algorithms are typically hundreds to thousands times slower than symmetric key algorithms due to the extremely large word lengths and c omplex

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 2

ISS N 2229-5518

operations like Modular exponentiation (ax mod n) etc.

2.2 Advantages o f ECC

The primary advantage is that ECC is based on either integer factorization or the discrete log problem in the multiplicative group of a finite field in the absence of a su b exponential-time algorithm. ECC uses smaller key size as compared to RSA. As a result it achieves greater speed and less storage.
There are various standard bodies guiding the implementation of security protocols for the industry. Some of the organizations involved in standard activities are the Internet Engineering Task Force (IETF), American Bankers Association, International Telecommunications Union, IEEE P1363[2], and National Institute of Standards and Technology (NIST)[3], ANSI X9.62[4], ISO 11770 -3 and ANSI X9.63.
The US National Institute for Standards and Technology has recommended up to 2010 that these 1024 -bit systems are sufficient [5] as shown in Table 1. After wards, NIST recommends key size should be upgraded for providing more security. ECC is becoming the mainstream cryptographic scheme in all mobile and wireless devices. ECC can be broadly divided in to four categories: the Internet, smart cards, PDAs and PCs [6 ].

TABLE 1

NIST RECOMMENDED KEY SIZES[5]

This paper focuses on Asymmetric algorithm using ECC. In
1985 Koblitz and V. Miller independently proposed using
the group of points on an elliptic curve defined over a finite field in discrete log cryptosystems.
This survey presents the current research in the high speed
hardware implementation of ECC. Note that the problem of side channel attacks and also Hyper Ellip tic Curve Cryptography are not within the scope of this study. The aim of this survey is to highlight the work carried out in implementing ECC on FPGA for desired level of efficiency and flexibility.

3. ELLIPTIC CUR VE SYSTEM [1] [7] [8] [9] [10] [11]

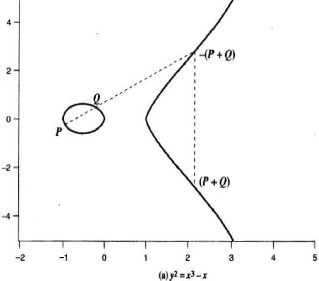
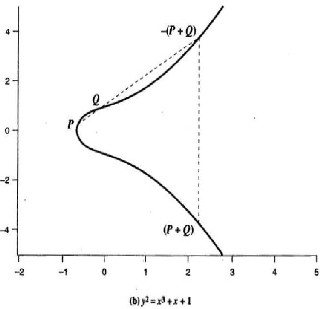
An elliptic curve is defined by an algebraic equation in two variables. For cryptography, the variables and the coefficients of the equation are restricted to elements in a finite field. This results in the definition of a finite Abelian group [12].This section presents, quick review about the background of elliptic curve system. For a thorough description of the topic, the reader is referred to the literature [12].

3.1 Elliptic Cu rve s over real numbers

Elliptic curves are not ellipses. They are so named because they are described by cubic equations;
In general, cubic equations for elliptic curves take the form y2+axy+by =x3+cx2+dx+e,
Where a, b, c, d and e are real numbers and x and y take on values in the real numbers.
It is sufficient to limit ourselves to equations of the form y2 =x3 +ax+b ----- (1)
Such equations are said to be cubic, or of degree 3, because
the highest exponent they
contain is a 3.Also included in the definition of an elliptic curve is a single elementdenotedo and called the point at
infinity or the zero point, To plot such a curve, we needto computeY =
For given values of a and b, the plot consists of positive and
negative values of y for
each value of x. Thus each curve is symmetric about y =0.
Figure 1 shows the two examples of elliptic curves [1].

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 3

ISS N 2229-5518

not negatives of each other,
the slope of the line l that joins them is
∆ = (y2- y1)/( x2– x1).
After some algebraic manipulation, we can express the sum
R = P + Q as follows:
xR = ∆2 –x1 – x2
yR = - y1 + ∆( x1- xR) ………………..(3)
We also need to be able to add a point to itself: P + P= 2P = R, when y1 = 0,
The expressions are
xR =( (3x21 + a)/(2y1))2 – 2x1
yR =((3x2
+ a)/(2y1)) (x1-xR) –y1 …………(4)

3.2 Elliptic Cu rve s over Zp

Two families of elliptic curves are used in cryptographic applications: prime curves over Zp and binary curves over GF(2m)
For a Elliptic Curve over Zp; we use a cubic equation in which the variables and coefficients all take on values in the set of integers from 0 through P -1 and in which calculations are performed modulo P.For elliptic curves over Zp, as with real numbers, coefficients and variables limited to Zp:
y2 mod P = (x3 + ax + b) mod P ..............(5)
Group can be defined ba sed on the set Ep( a, b) provided that (x3 + ax + b) mod P has no repeated factors. This equivalent to the condition
(4a3 +27b2) modP≠ 0 mod P……………(6)
Figure1. Examples of Elliptic Curves [1].
Group can be defined based on the set E(a,b) for specific values of a and b in equation (1), provided the following condition is met:
4a3 + 27b2 ≠ 0 …………………….(2)
Rules of addition over an elliptic curve are as follows: (a) P + 0 =0 + P = P for all P E.
(b) P + (-P) = 0 for all P  E.
(c) P + (Q + R) = (P + Q) + R for all P; Q; R  E.
(d) P + Q = Q + P for all P; Q  E.
With the preceding list of rules, it can be shown that the set
E(a, b) is an abelian group.
For two distinct points P = (x1, y1) and Q = (x2, y2) that are
The rules for addition over Ep (a, b) correspond to the algebraic technique described for
elliptic curves defined over real number. For all points P, Q
Є Ep (a, b):
1. P + 0= P
2. If P =(x1, y1), then P + (x1, -y1) = 0. The point (x1, -y1) is the negative of P,denoted as –P.
3. If P =(x1, y1) and Q = (x2, y2) with P≠ -Q,
then R = P + Q = (xR, yR) isdetermined by the following rules:
xR = (λ2 – x1 – x2) mod P
yR = (λ(x1 –xR) – y1) mod P Where

(y2 – y1)/(x2– x1) mod P if P≠ Q
λ=
((3x21 + a)/(2y1)) mod P if P= Q

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 4

ISS N 2229-5518

3. Multiplication is defined as repeated addition; for example, 4P = P + P + P + P.

3.3 Binary Curve over GF(2m)

For a binary curve defined over GF(2 m), the variables and coefficients all take on values
in GF( 2n) and in calculations are performed over GF(2 n).
A finite field GF(2m) consists of 2m elements, together with addition and multiplicationoperations that can be defined over polynomials. It turns out that the form of cubicequation appropriate for cryptographic applications for elliptic curves is somewhatdifferent for GF(2m) than for Zp. The form is
y2 + xy = x3 + ax2 + b ……(7)
The variables x and y and the coefficients a and b are elements of GF(2m) and thatcalculations are performed in GF(2m).
1. P + 0= P
2. If P = (x1, y1), then P + (x1, x1 + y1) = 0. The point (x1, x1 +
y1) is the negative ofP, denoted as –P.
3. If P = (x1, y1) and Q=(x2,y2) with P≠ - Q and P≠ Q, then R
= P + Q = (xR, yR) isdetermined by the following rules:
xR = λ2+ λ+ x1+ x2 + a yR= λ( x1+ xR )+ xR+y1
Where
λ = (( y2+ y1 )/ ( x2+ x1 ))
4. If P = ( x1, y1) then R = 2P = ( xR, yR ) is determined by the following rules:
xR= λ2+ λ+ a
yR = x21 +(λ + 1 )xR
where
λ = x1 + (y1/x1)

4. EX ISTING MULTIPLICATI ON ALGORITHMS IN ECC [13]

4.1 Binary Scalar Multiplication Algorithm s

Algorithm 1: Le ft-to-right binary algorithm

Input: P E( ), k=
Output: Q= [k]P
1.
2. for i=n-2 downto 0 do
3.
4. if then
5. end for
6. return

Algorithm 2: Right to le ft binary algorithm

Input: P E( ), k= Output: Q= [k]P
1.
2.
3.
4.
5.

6. return

The purpose is to select a simple but efficient multiplication algorithm. Hence we choose the best available one which is binary scalar multiplication which in the context of ECC is known as square and multiply algorithm or double-and- add algorithm. The binary algorithm processes a loop scanning the bits of the scalar and performing a point doubling, followed by a point addition whenever the current scalar bit equals 1.Two methods can be used in this case: left to right or the right to left direction

On an average both the algorithms involve n point doublings and n/2 additions. Using a signed representation for the exponent the number of point additions can be reduced by choosing a random number
The Non-Adjacent Form (NAF) which is a signed representation of the scalar has only n/3 signed bits. Hence the number of point additions falls to a much lower value of n/3.
This algorithm is fast and consumes low memory. If more
memory is available we can use window technique. In the
case of the above mentioned algorithm each loop focuses on a single bit whereas window technique focuses on a window of w bits. Every loop iteration in other words treats a scalar in the radix 2w. This variation of the Binary algorithm involving more memory is called Regular Signed Window Algorithm.

4.2The Montgomery Ladder Scalar Multiplication

Algorithm: Algorithm 3 :

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 5

ISS N 2229-5518

Input: P E( ), k= Output: Q= [k]P

1.

2.

3.

4.

5.

6.

In Montgomery Algorithm the condition R1 -R0=P is satisfied at the end of every iteration where R0 & R1 are the loop invariants [57]. This algorithm was initially proposed for a specific type of curves called Montgomery curves. Later however it was adapted to other elliptic curves. Since only X and Z coordinates are computed, the resources that would otherwise be lost on Y coordinates is saved thereby improving efficiency. It involves the computation of the sum of the coordinates whose difference is known, also known as the Differential addition.
Another feature that could be added to the benefit of Montgomery Algorithm is the use of (X,Y)-only co-Z arithmetic technique. The loop iterations of the Montgomery Algorithm can be rewritten to perform conjugate addition followed by regular addition as shown:

4.3 The Joye Double and Add Algorithm

Algorithm 4 :

Input:PE( ), k= Output: Q= [k]P
1.
2.
3.
4.
5.
6.
In Joye Algorithm the ith loop iteration yields R0+R1=[2 i]P. It hence produces a efficient regular scalar multiplication based on co-Z addition formulae along the lines of Montgomery ladder technique. The efficiency is akin to that of Montgomery technique.

4.4 Classical Multiplication Algorithm[14]

This algorithm is nothing but a direct translation of the regular multiplication technique. Consider the problem of multiplication of any two Polynomials of degree n:
We need to find all the coefficients of the polynomial
C(x)=A(x)B(x) For example :
Let us consider two general polynomials A(x) and B(x) of degree n and m respectively. Then the resultant polynomial C(x) is of degree m+n and the vector (C0,C1,…,Cm+n) is a convolution of vectors (a0,a1,..,an) and (b0,b1,…,bm).
Let and
Set
Then
Calculating these convolutions is a major problem in digital signal processing.Thus the cost calculation becomes vital. The cost of the Classic Multiplication Algorithm works out
to be Ɵ(n2).Also this type of multiplication requires n2 multiplications and (n-1)2 additions.A more subtle way of achieving this is carrying out the divide and conquer multiplication based on Karatsuba’s multiplication algorithm.

4.5 Karatsuba Multiplication Algorithm[14]

The Karatsuba algorithm is a fast multiplication algorithm published in 1962. It reduces the multiplication of two n - digit numbers to at most 3n log 3 3n1.585 single-digit multiplications in general (and exactly nlog 3 when n is a
power of 2). It is therefore faster than the classical
algorithm, which requires n 2 single-digit products.The application of Karatsuba’s Algorithm on multiplication of Polynomials is illustrated below:

The Divide Ste p: Define

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 6

ISS N 2229-5518

The coordinate systems are chosen to avoid costly final inversions. The following coordinate systems are available:

5.1Affine Coordinate System

Similarly we define and such that

Then

The Co nque r Ste p: Solve the four sub problems, i.e., computing

The Affine coordinate system is the conventional Cartesian coordinate system. Hence the equation of Elliptic curve in Affine Coordinate system is given by:
y2 + xy = ax2 + b (b≠0)
Point doubling and addition operations used in ECC require inversion operation and multiplication requires more inversions than adding and squaring. Division is implemented using inversion. Given two points P(x1,y1) and Q(x2,y2),a third point R(x3,y3) given by addition of P and Q, that is R=P+Q, then the coordinates of R are given by:



,
By recursively calling the algorithm 4 times.

The Co mbining Ste p: Adding the following four polynomials

This reduces the number of operations to (n)
Iterative Karatsuba’s Multiplication Algorithm (IKM) operates similar to Karatsuba’s Multiplication Algorithm in the sense that it splits the operands into parts but different in the aspect that the partial multiplications proceed iteratively instead of a single monolithic multiplication and the results are accumulated to the final result.
Today’s research concentrates on improving these primary
algorithms for better performance.

5. C HOICE OF COORDINATES [ 15, 16, 17, 18 ]

Requiring computation of two inversions, it becomes too costly in terms of hardware implementation. Hence we present the use of Projective coordinates.

5.2 Projective Coordinates

The Projective Coordinate system is a three coordinate system with X,Y Z coordinates used to represent a point. The equation of an elliptic curve in Projective Coordinates is given by :
Y2 + XYZ = X3Z + aX2Z2 + bZ4
Since selection of the proposed Projective Coordinates avoids the cost due to inversion, this coordinate system is highly favored.
The three currently popular projective coordinates are:
1. Homogenous Projective Coordinates
2. Jacobian Projective Coordinates

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 7

ISS N 2229-5518

(X, Y, Z) (X/Z2, X/Z3) in Affine
3. Lopez-Dahab Projective Coordinates
(X, Y, Z) (X/Z, X/Z2) in Affine
Among the three the computation cost of L-D system is lowest and hence most efficient system for Hardware implementation.A comparison between the above mentioned Coordinate systems in terms of cost is shown in table2:
Table 2

Final Inversion is however necessary to convert to Affine Coordinate system from the Projective coordinates at the end of the computation.

6. R ELATED WORK ON FPG A:

So far several papers on high-speed architecture for implementation of ECC operations have been published. In this section we review these implementations on FPGA.
Owing to the their re-configurability due to which accelerator can easily be changed to keep up with ever changing security requirements, FPGA’s are advantageous for implementing cryptographic hardware accelerators
.Implementations on FPGA have thus been selected for this.
We present the corresponding implementations on Xilinx Virtex FPGA in Table3.Related references can be found in [61,62]
A novel memory architecture was proposed [19],which was advantageous for distributed memory architecture, well-suited for different point addition and doubling algorithms over GF(p) implemented on FPGAs [19]. Point addition and point doubling operations in ECC are performed in Affine coordinates, implemented on FPGA .This work is secure against time and power analysis attacks[22].The results of paper [22] have been summarized in Table 3.
The proposed crypto-processor uses a Parallelized Modular Arithmetic Logic Unit(P-MALU) that exploits two types of different parallelism to accelerate modular operations. Multiple P-MALU instructions are processed in parallel and using Instruction -Level Parallelism(ILP) scalar multiplications areaccelerated. [20]. A GF(p) 160-bit ALU for encryption processors was proposed.[50].The results of which[50] is summarized in Table3. A unified arithmetic unit was proposed for dual field modular operations and an adder based on signed-digit number representation that provides for both carry-propagated and carry-
less operations was proposed [27] [53].The paper [27] [53]
also gives FPGA results in table 3.
FPGA implementations of the EC point multiplication over GF(2283) was proposed that can speed up by 31.6 times in comparison to previous approaches[28]. Flexible elliptic curve cryptography processors and their implementation on FPGA are described in [58] . The relevant results are
shown in table 3. This paper [55] presents FPGA
architecture which contribute to acceleration of ECC operations. The aim is primarily to reduce the latency of point multiplication operations in terms of number of required cycles. A processor architecture for Elliptic Curve Cryptography Computations over GF(p) was proposed using parallelism and selecting appropriate coordinate system the speed of computations was significantly enhanced. It was implemented on FPGA.[17]. A new architecture for cryptoprocessor is proposed which can compute point multiplication with arbitrary point over Elliptic curves over GF(p).[49].The results of which [49] have been tabulated in table 3.This paper[59] proposes a novel FPGA coprocessor for ECC that makes use of a partial reconfigurable methodology to deal with interoperability problems . This paper gives the result in table 3.
Different reconfigurable modular multiplication methods and modular reduction methods for software implementation on Intel IA-32 processor were compared and the point arithmetic was optimized by reduction sharing technique. [21]
The novel reduction algorithm presented in this paper supports seldom used curves and arbitrary curves unknown at the time of implementation and for several field degrees it permits software and hardware implementations [25]. Improved multiplier design is proposed over both named and generic curves which implements 256 bit modular field operations and results are discussed for 163-bit[37] as shown in table 3.

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 8

ISS N 2229-5518

An improved Montgomery multiplier based upon four-to two CSA was proposed to reduce path delay. A modified CSA based on single level carry-save logic is used here. The need for extra clock cycles for operands whose length was not a power of 2 was eliminated using reconfiguration of the design [26].
A novel partitioning and pipeline folding scheme to fit at least 512-bit modular multiplications on a single FPGA is achieved [40]. A customizable pipelined and parallelized ECC design for various field operations has been proposed [39.] The EC cryptographic processor proposed in this work has finite-field (FF) RISC cores and a main controller to achieve instruction level parallelism(ILP) for EC point multiplication [29].This paper[30] focuses on two different architectures based on parallelism to speed up the EC point multiplications in Affine coordinates. It also discusses the results in table 3 [30]. A high performance architecture for scalar multiplication over EC
GF(2m)has been proposed. A pseudo-pipelined word serial finite field multiplier with word size w, suitable for the scalar multiplication is also developed [45]This paper[45] discusses the result in table 3.
A new coordinate system and arithmetic implementations of ECC over GF(2n) was proposed [18].This coordinate system resulted in improved efficiency
and performance in terms of speed.
A micro-coded EC processor with low memory and computation requirements with a high degree of security is proposed [33].A high performance ECC processor based on Lopez-Dahab EC point multiplication was proposed.[31],[35].The paper[31] also gives FPGA results in table 3.
A hardware architecture for implementing scalar multiplication using polynomial basis was proposed.[47].The result is included in table 3 at reference [46,47] .A parallel architecture for scalar multiplication based on Karatsuba’s multiplication algorithm over
Hessian Curves in GF(2m) has been proposed[44].The results of this work[44] have been discussed. Point multiplication is the most crucial among the ECC operations. This architecture[56] uses the polynomial multiplication as the basis to compute the product over
GF(p) or GF(2m).
A novel high speed and low area, array and polynomial based architecture for field operations such as multiplication and squaring over GF(2 m) has been
proposed.[22]. Hardware implementation of an arithmetic
processor involving Montgomery modular multiplication
in a systolic array architecture is described [24].The corresponding result is included in table 3. The two new hardware architectures for Montgomery modular multiplication for radix-2 is proposed and compared with the previous architectures.[23].The implementation of Montgomery Multipliers using higher radix.(radix -2,4,8,64) is achieved[32].and the concurrent algorithm is discussed to speed up point multiplication[38]Higher radix EC cryptographic architecture is achieved by applying sliding window scalar multiplication algorithm as used[41], 1’s complement fast scalar multiplication[42]is used, a pipelined application specific instruction set processor(ASIP) is used[43], to achieve higher speed. The paper [43] gives the result in table 3.
A dual-mode Arithmetic Unit(AU) capable of performing field operations of both ECC and RSA schemes based on Montgomery Multiplication is proposed[46] An EC processor with a new multiplier architecture for high - radix multiplication has been proposed[48]. The results of which[48] have been presented in Table 3. This paper[54] proposes architecture based on Montgomery parallel multiplier. It is defined over GF(p). A dual field EC processor with projective coordinates adaptive to both binary and prime fields, implementing the scalar multiplication architecture was proposed. Better time, area performance and lower power consumption was observed [34][36].In this paper a new arithmetic unit is proposed that uses Polynomial modular multiplication of ECC over binary field. The result of this paper [60] has been presented in table 3.
A simple generator is proposed in[51] and the improved version is presented in [52].These two papers[51][52]mention the result in table 3.

7. PERFORM ANCE SUMM ARY

In an effort to showcase the works conducted so far in the relevant field , we have chosen only the most appropriate results in our opinion. These results aresummarized in the table 3. XCV devices are Xilinx Virtex FPGAs. LUTs are Look Up Tables, CLBs are Configurable Logic Blocks, LSD/MSD is Least/Most Significant Digit, D is Digit size of a serial/parallel multiplier, bRAMs is nothing but Block RAMs, DBLand ADD is Double and ADD, ASIP is Application Specific Instruction set Processor, CSA is Carry Save Adder and GNB is Gaussian
Normal Basis.

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 9

ISS N 2229-5518

Table3: Performance summary of state of the art

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 10

ISS N 2229-5518

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 11

ISS N 2229-5518

8. C ONCLUSION

Selecting a hardware architecture design for the ECC system presents a trade-off between flexibility and speed. Hardware accelerators used for high performances sacrifice flexibility. In any architecture , multiplication, terminal inversion to affine coordinates becomes primarily important and they tend to govern the speed and efficiency of the proposed architecture. The architecture must also be able to support various cryptosystems. Selection of an efficient coordinate system(Jacobian ,Affine, Lopez -Dahab etc) and a fast scalar multiplication algorithm (Montgomery, Karatsuba, Binary Scalar etc )are also significant. In our opinion the Lopez -Dahab coordinates was found to be a good choice of coordinates. Therefore to develop an efficient architecture a wise combination of both has to be made. Usage of parallelism in multiplication results in significant speedup. Parallelism may be enhanced using pre-computed partial results. Using a higher radix Montgomery multiplication with Carry Save Adders also
provides a high performance. Partial reduction technique
could be implemented.
The architecture must also ens ure that integration of large multipliers should result in a noticeable speedup . Finally a suitable algorithm for inversion of coordinates to Affine must also be decided upon.
Adding a note on future work, study is being conducted on developing a cryptographic processor that can use a common architecture for point multiplication for both GF(p) and GF(2m). Currently
work is in progress to achieve functional extensions and optimizations such as speed improvement, resource minimization, and run-time customization of ECC designs.Further improvements could include enhancement in resistance of ECC processors to side channel attacks by enabling clock-stealers and other counter measures that would force the attacker to make large data requisitions.

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 12

ISS N 2229-5518

9. REFEREN CES

[1].Stallings W, ―Network and internetwork security principles and practice‖.1995, Prentice Hall, New York,USA
[2] IEEE P1363, ―Standard Specifications for Public Key
Cryptography,‖ 2000.
[3] ―Digital Signature Standard (DSS)‖, Federal Information Processing Standards Publication 186 -2, National Institute of Standards and Technology. 2000.
[4] ANSI, ANSI X9.62 ―The elliptic curve digital signature algorithm (ECDSA‖).
[5] nsa.gov.. ―The Case for Elliptic Curve Cryptography‖. Retrieved from The National Security Agency Central Security Service.,2009.
[6] Wendy Chou, Dr. Lawrence Washington ,―Elliptic Curve Cryptography and Its Applications to Mobile Devices‖.Department of Mathematics, University of Maryland, College Park.
[7] Koblitz, N..―Elliptic curve cryptosystems.Mathematics of Computation‖,1987.
[8] Miller,V,‖Use of elliptic curves in cryptograph‖y.CRYPTO 85.1985.
[9] Lay, G.-J., & Zimmer, H. G..―Constructing elliptic curves with given group order over large finite fields‖. Proceedings of the First International Symposium on Algorithmic Number Theory. Springer Lecture Notes In Computer Science;1998, Vol. 877.
[10] Rosing, M..―Implementation Elliptic Curve
Cryptography‖.Manning Pub.,1999.
[11] Blake, I. F .‖Advances in Elliptic Curve Cryptography‖. Cambridge University Press Series: London Mathematical Society Lecture Note Series,2005.
[12] I. Blake, G. Seroussi, N.P. Smart, ―Elliptic curves in cryptography‖, London Mathematical Society Lecture NoteSeries, 1999.
[13] MatthieuRivain,.‖Fast and Regular Algorithms for
Scalar Multiplication over Elliptic Curves‖, 2011.
[14] Steffen Peter and Peter Langend¨orfer,‖ An Efficient Polynomial Multiplier in GF(2m) and its Application to ECC Designs‖,2007 EDAA
[15] Prof.Rahila Bilal Dr.M.Rajaram, ―High Speed and Low Space Complexity FPGA Based ECC Processor‖,International Journal of Computer Applications (0975 – 8887) ,Volume 8– No.3, October 2010.
[16] Maurice Keller, Andrew Byrne and William P. Marnane, ―Elliptic Curve Cryptography on FPGA for Low- Power Applications‖, ACM Transactions on Reconfigurable Technology and Systems, Vol. 2, No. 1, Article 2, Pub. date: March 2009.
[17] Lo’ai Ali Tawalbeh& Abidalrahman Mohammad & Adnan Abdul-Aziz Gutub, ―Efficient FPGA Implementation of a Programmable Architecture for GF(p) Elliptic Curve Crypto Computations‖, 59:233-244 DOI
10.1007/s11265-009-037-x,Springer,2010.
[18]J. Lo´ pez, R. Dahab, ―Fast multiplication on elliptic curves over GF(2m), in: Cryptographic Hardware and Embedded Systems (CHES)‖, LNCS 1717, 1999, pp. 316 -327
[19] RALF LAUE AND SORIN A. HUSS, ―Parallel Memory Architecture for Elliptic Curve Cryptography over GF(P) Aimed at Efficient FPGA Implementation ‖, Journal of Signal Processing Systems 51, 39–55, Springer Science + Business Media, 2008.
[20]Kazuo Sakiyama,LejlaBatina , Bart Preneel, Ingrid Verbauwhede, ―High-performance Public-key Cryptoprocessor for Wireless Mobile Applications‖, Published online: 3 October 2007 , Springer Science + Business Media,
[21]Aaron E. Cohen , Keshab K. Parhi,‖Fast Reconfigurable Elliptic Curve Cryptography Acceleration for GF(2m) on 32 bit Processors‖, Published online: 1 July 2009, Springer Science + Business Media.
[22]SantoshGhosh, MonjurAlam, Dipanwita Roy Chowdhury and IndranilSenGupta,‖A GF(p) Elliptic Curve Group Operator Resistant Against Side Channel Attacks‖, GLSVLSI’08, May 4–6, 2008, Orlando, Florida, USA,ACM
978-1-59593-999-9/08/05
[23] MiaoqingHuang,Krisgaj,Tarek El-Ghazawi, ―New
Hardware Architecture for Montgomery Modular

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 13

ISS N 2229-5518

Multiplication Algorithm‖,IEEE Transactions on
Computers, VOL,60,NO.7,JULY 2011,DOI NO.
10.1109/TC.2010.247
[24] SıddıkaBernaOrs, LejlaBatina, Bart Prenee, JoosVandewalle, ―Hardware Implementation of an Elliptic Curve Processor over GF(p)‖, Proceedings of the Application-Specific Systems, Architectures, and Processors (ASAP’03), 2003 IEEE.
[25] Nils Gura, Hans Eberle, Chang Shantz,‖ Generic Implementations of Elliptic Curve Cryptography using Partial Reduction‖, NOV18-22, 2002,Washington, DC, USA.ACM 1-58113-612-9./02/0011
[26] M. Sudhakar& R. V. Kamala &M. B. Srinivas, ―New and Improved Architectures for Montgomery Modular Multiplication‖,Springer Science + Business Media, 2007 .
[27] Yi Wang,DouglasL.Maskell, JussipekkaLeiwo,‖A Unified Architecture for a Public Key Cryptographic Coprocessor‖ .JSA 2008,Elsevier
[28]Hao Li a,*, Jian Huang b, Philip Sweany a, Dijiang Huang c, ―FPGA implementations of elliptic curve cryptography and Tate pairing over a binary field‖, Journal of Systems Architecture 54 ,2008, 1077–1088,Elsevier
[29] Yu Zhang, Dongdong Chen, Younhee Choi, Li Chen, Seok-Bum Ko, ―A high performance ECC hardware implementation with instruction -level parallelism over GF(2163)‖, Elsevier B.V,doi:10.1016/j.micpro.2010.04.006
[30]SantoshGhosh *, MonjurAlam, Dipanwita Roy Chowdhury, IndranilSenGupta, ―Parallel crypto-devices for GF(p) elliptic curve multiplication resistant against side channel attacks‖,2009,Elsevier Ltd,doi:10.1016/j.compleceng.2008.06.09
[31] Chang Hoon Kim, Soonhak Kwon, Chun Pyo Hong
,‖FPGA implementation of high performance elliptic curve cryptographic processor over GF(2163)‖,Journal of Systems Architecture 54 ,2008 893–900, Elsevier B.V.,
[32]GashawSassaw, Carlos J. Jimenez, Manuel Valencia,
―High Radix Implementation of Montgomery Multipliers with CSA‖, 22nd International Conference on Microelectronics (ICM 2010),2009 IEEE
[33]R.Dhanagopal, B.Manivasakam, ―FPGA implementation of public keyprocessor for network security‖, 2010 IEEE
[34] B.MuthuKumar, S.Jeevananthan,‖High Speed Hardware Implementation of an EllipticCurve Cryptography (ECC) Co-Processor‖, 2010 IEEE
[35] A.Kaleel Rahuman, Dr. G.Athisha, ―Reconfigurable Architecture for Elliptic CurveCryptography‖,Proceedings of the International Conference on Communication and Computational Intelligence – 2010, Kongu Engineering College, Perundurai, Erode, T.N.,India.27 – 29
December,2010.
[36]Prabhat Chandra Shrivastava, Rupesh Kumar, Arvind Kumar, SanjeevRai,‖ High-Speed and Low Power Unified Dual-Field Multiplier in GF (P) and GF (2m)‖,2010 IEEE
[37] H. Eberle, N. Gura, S. Chang-Shantz, ―A cryptographic processor for arbitrary elliptic curves over GF(2 m)‖, in: Application-Specific Systems, Architectures, and Processors,(ASAP), 2003,
[38]Jun-Hong Chen, Ming-Der Shieh and Chien-Ming Wu,Concurrent Algorithm for High-Speed Point Multiplicationin Elliptic Curve Cryptography, 2005 IEEE
[39] Ray C. C. Cheung, Nicolas Jean -baptisteTelle, Wayne Luk, Peter Y. K. Cheung,‖ Customizable Elliptic Curve Cryptosystems‖, IEEE transactions on very large scale integration (VLSI) systems, vol. 13, no. 9, September 2005.
[40] Osama Al-Khaleel, KiamalPekmestzi, ―FPGA-based Design of a Large Moduli Multiplierfor Public -Key Cryptographic Systems‖, 2006 IEEE
[41] Mohamed A. Fayed, M. Watheq El-Kharashi, Fayez Gebali, ―A High-Speed, High-Radix, Processor Array Architecture for Real-Time Elliptic Curve Cryptography Over GF(2m)‖, 2007 IEEE
[42] Xu Huang, Pritam Gajkumar Shah, Dharmendra Sharma, ―Fast Scalar Multiplication for Elliptic Curve Cryptography in Sensor Networks with Hidden Generator Point‖, International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, 2010
IEEE

IJSER © 2012 http :// www.ijser.org

Inte rnatio nal Jo urnal o f Sc ie ntific & Eng inee ring Re se arc h Vo lume 3, Issue 3, Marc h -2012 14

ISS N 2229-5518

[43] William N. Chelton, Mohammed Benaissa,‖Fast Elliptic Curve Cryptography on FPGA‖,IEEE Transactions on VLSI system, 2007 IEEE
[44] Nazar A. Saqib, Francisco Rodr´ıguez -Henriquez and Arturo D´ıaz-P´erez, ―A Parallel Architecture for Computing Scalar Multiplication on Hessian Elliptic Curves‖, Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC’04)2004 IEEE
[45] B. Ansari, M. Anwar Hasan, ―High performance architecture of elliptic curve scalar multiplication ‖, Tech. Report CACR 2006-01, 2006.
[46] F. Crowe, A. Daly, W. Marnane, ―A scalable dual mode arithmetic unit for publickey cryptosystems‖, in: International Conference on Information Technology:Coding and Computing ITCC’05 ,IEEE
[47] Miguel Morales-Sandoval ,Claudia Feregrino-Uribe,on the ―Hardware Design of an Elliptic Curve Cryptosystem‖, Proceedings of the Fifth Mexican International Conference in Computer Science, 2004 IEEE.
[48] G. Orlando, C. Paar, A Scalable GF(p),‖ Elliptic Curve Processor Architecture forProgrammable Hardware‖, CHES 2001, LNCS 2162, Springer-Verlag, 2001.
[49] W. Shuhua and Z. Yuefei, ―A Timing and Area Tradeoff GF(p) Elliptic Curve Processor Architecture for FPGA‖, ICCCAS’05, pp. 1308–1312, IEEE
[50] A. Daly, W. Marnane, T. Kerins and E. Popovici, ―An FPGA Implementation of a GF(p) ALU for Encryption Processors‖, Microprocessors and Microsystems, Vol. 28, pages 253–260, ,2004 Elsevier
[51] ] K. Ja¨rvinen, M. Tommiska, J. Skytta¨, ―A scalable architecture for elliptic curve point multiplication ‖, in: IEEE Field- Programmable Technology (FPT), 2004
[52] C. Grabbe, M. Bednara, J. von zurGathen, J. Shokrollahi, J. Teich,‖ A high performance vliw processor
for finite field arithmetic‖, in: Reconfigurable Architectures
Workshop (RAW), 2003.
[53] A. Cilardo, A. Mazzeo, N. Mazzocca, L. Romano, ―A novel unified architecture forpublic key cryptography‖, in: IEEE Proceeding of the Design, Automation andTest in Europe Conference and Exhibition, vol. 3, 2005.
[54] C. McIvor, M. McLoone, J. McCanny, ―An FPGA ellipticcurve cryptographic accelerator over GF(p)‖, in: Irish Signalsand Systems Conference (ISSC), 2004
[55] N. Gura, S.C. Shantz, H. Eberle, S. Gupta, V. Gupta , D. Finchelstein, E. Goupy, D.Stebila, ―An end-to-end systems approach to elliptic curve cryptography‖, in:CHES 2002, Lecture Notes in Computer Science.
[56] C. Shu, K. Gaj, T. El-Ghazawi, ―Low latency elliptic curve cryptography accelerators for NIST curves on binary fields‖, in: IEEE Field-Programmable Technology (FPT),
2005.
[57].Montgomery,P.‖Modular Multiplication without trial division‖.Mathematics on Computation, 1985.
[58] M. Benaissa, W.M. Lim, ―Design of flexible GF(2 m) elliptic curve cryptographyprocessors‖, IEEE Transactions on VLSI System 2006.
[59] M. Morales-Sandoval, C. Feregrino-Uribe2,⋄ , R.
Cumplido and I. Algredo-Badillo , ‖A Reconfigurable
GF(2m) Elliptic Curve Cryptographic Coprocessor‖,
2011,IEEE
[60] Yi Wang and Renfa Li,‖ A Unified Architecture for
Supporting Operations of AES and ECC‖ ,2011, IEEE
[61].VirtexTM-E 1.8V ―Field Programmable Gate
Arrays‖,http://www.xilinx.com/bvdocs/publications/ds0
22.pdf
[62].Virtex-II Pro and Virtex-II Pro X Platform
FPGAs:Complete Data Sheet http:// www.xilinx.xom/
bvdocs/publications/ds083.pdf

Shylashree N is currently a Research Scholar,

in E.C.E, at PESCE, Mandya, Karnataka, India and is also

working as faculty at R.N.S.I.T, Bangalore, Karnataka, India.

IJSER © 2012 http :// www.ijser.org

International Journal of Scientific & Ergineerirg Research Volume 3, IsstE 3, March -2012 15

lSSN 2229-5518

shylamami@gmail.rom

Nagarjun Bhat ismrrentlypursuing B.E(4th semester), in E.C.E, at R.N.S.I.T, Bangalore, Karrmtaka, India einstein.nag@gmailcom

V Sridhar is Professor in E.C E and Principal atP.E.S.C.E, Mmdya, Karrmtaka,India venusridhar@yahoo.com

1-BER <b)2012

rttp: 1/ WWI'I.I!ser.crg