International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1139
ISSN 2229-5518
Effect of Self-Gravitating Viscous Radiative and Thermally Conducting Gaseous Plasma in the Presence of Fine-Dust-Particles under the Effect of Finite Electron Inertia and Heat-Loss function
Abstract :-
R.K.Pensia*, V.Prajapat**, V.Kumar**, G.S.Kachhawa**, D.L.Suthar***
*Department of Physics, Govt. Girls College, Neemuch
**Department of Physics, Pacific University, Udaipur
***Department of Physics, Mewar University, Chitorgarh
*Email: vikasprajapat712@Gmail.com
The Effect of self-gravitational instability of an infinite homogeneous, viscous and magnetized gas particle medium in the presence of fine- dust- particles has been studied in corporating thermal conductivity and arbitrary or radiative heat-loss functions. From linearized equations of the system, a general dispersion relation is obtained using normal mode analysis.The conditions of modified Jeans instability and stability are discussed in the different cases of our intersest. We find that the presence of arbitrary radiative heat-loss functions and thermal conductivity modifies the fundamental Jeans condition of gravitational instability into a radiative instability condition. It is found that the radiative modes of instability arises in the medium depends on the arbitrary radiative heat-loss functions on the local density and temperature of the system. Applying Routh –Hurvitz criterion, the stability of the medium is discussed and it is found that Jeans criterion determines the stability of the medium Thermal Conductivity modifies the Jeans criterion and the viscosity has damping effect. It is found that the effect of fine-dust-particles is to destabilize the system. It is also found that the condition of instability for propagation parallel to the magnetic field is independent of the magnetic field strength. For transverses propagation, however, the condition of instability depends on the magnetic field strength.
Key – Words: Heat- loss Functions, fine-dust-Particles, Gravitational Instability, Thermal Conductivity, Finite Electron Inertia and Viscosity.
1. Introduction:-
The fragmentation of interstellar matter is a vitally important phenomenon in star formation. The gravitational instability of an infinite homogeneous self-gravitating gas was first investigated by Jeans[1]. Latter, in view of existence interstellar magnetic field Chandrasekhar[2] has re-analyzed the same problem. Jeans[3] analysed the gravitational instability in an infinite homogenous medium, who derived the expression for maximum size of a uniform gravitating mass which is stable to small fluctuations in density[4]. The effect of fine-dust-particles on the gravitational instability of an infinite homogeneous gas particle medium has been investigated by Sharma[5].
In addition to this, the problem of magneto-gravitational instability of interstellar is of considerable importance in connection with protostar and star formation in magnetic dusty clouds. Magnetic field can provide pressure support and inhibit the contraction and fragmentation of interstellar clouds.Langer[6]has investigated the stability of interstellar clouds against gravitational collapse and fragmentation in the presence of magnetic field.. The problem of star formation in clouds containing magnetic field has been analyzed by Mestel and Spitzer[7]and they have derived a stability criterion, in the form of a Jeans length for collapse based on the virial theorem.
The nature of the coupling of the magnetic field to the neutrals through ion-neutral collisions has been analyzed by Spitzer[8-9]. A group of authors led by Sharma[10-12] has dealt with various problems of fluid dynamics in presence of fine-dust-particles considering the effect of fine-dust-particles on the onset of Benard convection,
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1140
ISSN 2229-5518
gravitational and magneto-gravitational instabilities of an infinite conductiviting homogeneous
medium..Chhajlani[13] et.al. Investigated the effect of finite conductivity on magneto-gravitational instability and fine-dust-particles of a homogeneous medium. Chhajlani and Purohit[14] have studied the problem of stability of a self-gravitating, infinite homogeneous gas in the presence of fine-dust-particles incorporating magnetic field, finite Larmor radius corrections and Hall effect.
The thermal conductivity has also its importance in the study of the interstellar medium. Field[15] suggested that the observed filamentary condensations in nebulae may be due to thermal effects. The effect of thermal conductivity on magneto-gravitational instability incorporating different parameters has been studied by several authors [Vyas and Chhajlani[16], Chhajlani and Vaghela[17], Vaghela and Chhajlani[18-19] and Chhajlani and Parihar[20].The gravitational instability of an infinite homogeneous viscous thermal conducting plasma of finite electrical conductivity in the presence of hall currents has been investigated by Ali and Bhatia[21].
Along with this, it is well known that thermal and radiative effects play an important role in the stability investigations. Aggrawal and Talwar[22] have investigated the problems of magneto thermal instability having heat-loss function. Bora and Talwar[23-24] have studied the problem of thermal instability, having bearing on the formation of astrophysical condensations for a hydromagnetic field. The thermal instability in a star-gas system has been investigated by Talwar and Bora[25] Pensia[26-27] et.al. investigated the magneto-thermal instability of self gravitating viscous Hall plasma in the presence of fine-dust-particles.
In all the above mentioned studies. The effect of simultaneous inclusion of the thermal conductivity, radiative effects and fine-dust-particles on magento gravitational instability of a gas particle medium is not investigated. In view of the importance of radiative effects in astrophysical contexts, we have incorporated radiative effects in the investigation of self-gravitational instability of an infinite homogeneous, viscous, thermally conducting and magnetized gas particle medium in the presence of suspended particle medium. This aspect forms the subject matter of the present study. Although, the present treatment is also highly idealized but nevertheless of importance as it may be helpful in gaining an insight into the phenomenon of the gravitational instability.
2.Linearized perturbation Equation:-
We consider an infinite homogeneous self-gravitating gas particle medium of thermal conductivity having radiative heat-loss effects in the presence of fine-dust-particles and it is acted by a uniform vertical magnetic field H(O,O,H). Let u(u,v, ω ),v, ρ and N be the gas velocity, the particle velocity, the density of gas and the number density of particles. If we assume uniform particle size, spherical shape and small relative velocities between the two phases, then the net effect of particles on the gas is equivalent to an extra body force term per
unit volume KN(v -u) and is added to the momentum transfer equation for gas, where the constant K is given by
Stoke’s drag formula K = 6 πρυr
, r being the particle radius and υ is the kinetic viscosity of clean gas. Self-
gravitational attraction U is added with kinetic viscosity term in equation of motion for gas.
In writing the equation of motion for particles, we neglect the buoyancy force as its stabilizing effect for the case of two free boundaries is extremely small. Inter particles reactions are also ignored by assuming the
distance between particles to be too large compared with their diameters.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1141
ISSN 2229-5518
The stability of the system is investigated by writing the solutions to the full equations as initial state plus a
perturbation. The initial state of the system is taken to be quiescent layer with a uniform particle distribution. The equation thus obtained are linearized by neglecting the product of two perturbed quantities.
Hence the linearized perturbation equation for motion of such medium are:
∂u =
δ−p1 ∇ δU+∇ +( KN ) v −υu +
∇2u + 1 ∇ (∇ u )



∂tρ ρ

.
3

+ 1
4πρ
(∇× h ) × H
(1)

∂ δp = − ρ∇.u
∂t
(2)
δp = C2δρ
(3)
∇.h = 0
τ ∂ + 1 v = u
(4)

∂t
(5)


∂ h = ∇× (u × H ) + c
∂ ∇2h
2
Pe
∇2δU = −4πGδρ
(6)
(7)
1 ∂ δp −
γ p
∂ δρ+ρ L δρ+ L
δT − λ∇2δT = 0

( γ −1) ∂t



δp = δT + δρ


γ −1 ρ ∂t ρ T
(8)
p ρ T
(9)
Where
δρ, δp, δU, δT
and h(hx , hy, hz ) denote respectively the perturbation in density ρ , pressure p,
gravitational potential U, temperature T and magnetic field H , G is the gravitational constant, C is the velocity
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1142
ISSN 2229-5518
of sound,

τ = m K
and mN is the mass of particles per unit volume, Here
Lρ and L T
respectively denote
partial derivatives
∂L
and
∂L
of heat-loss function evaluated for the initial state and
ω is the


pe
∂ρ T
∂T ρ
electron plasma frequency.
3.Dispersion Relation:-
Let us assume the perturbation of all the quantities vary as
Exp.
i ( K x x + K z z + ωt )
(10)
Where ω is the growth rate of the perturbation and
K x , K z
are the wave numbers of the
perturbation along the x- and z- directions respectively such that
K 2 + K 2 = K 2
(11)
Combining equation (8) and (9), we get
α + σC2

δp = δρ
σ + β
(12)
Where σ = iω
1/2
C = γp
is the adiabatic velocity of sound in the medium and

ρ
2 2
α = ( γ −1)
T − L ρ + λK T
; β = ( γ −1) L T Tρ + λK T
L T



ρ ρ p p
(13)
We get the following equations from (1), using (2) - (7), (12) and variations
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1143
ISSN 2229-5518
τσ3 + σ2 1 + KNτ + 4 υK 2 τ + σ 4 υK 2 + (1 + σ τ )
K 2 V2
] u




ρ 3 3 sF

= − i K x Ω2 (1 + τσ ) σ s
K 2 T
(14)
[τσ3 + σ2 1 + KNτ + 4 υK2 τ + σ ( 4 υK 2 ) + (1 + σ τ )
K 2 V2
z ] v = 0




ρ 3 3 F
KNτ 4 4 −iK
τσ + σ 1 + + υK τ + υK ω = Ω 1 + τσ
(15)




ρ 3
3
K 2 T
(16)
On taking the divergence of equation (1), using (2) - (7), (12) and performing the above said variation we get
K 2 V2
−iK x τσ u 1 + +
F
τσ4 + σ3 1 + + υK 2 τ + υK 2σ2 + σ (1 + σ τ ) Ω2 s = 0



ρ 3 3 T
(17)
(14)-(17) can be written in the form

K 2 V2




iK x Ω2 ξ σ u

σξ3 + ξ2
F
0 0 K 2 T 2
K 2 V2
0 σξ3 + ξ2
z
F
0 0 v
iK z Ω2 ξ = 0

0 0 ξ3
K 2 T 2 ω
−iK

K V ξ
0 0 σ (σξ + ξ Ω2 ) s
x F 2 3 2 T
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1144
ISSN 2229-5518
Where

s = δρ ρ
(18)


1υ+ KNτ +ξ 4
2 =
ρ 3 1
(1σ+ τ
) ξ=
; τσ
2 σ+ 1


+ KNτ + 4

τ2 + 4
2 =ξ
υK υK
2 ρ 3
Ω2 =
σΩ2 + Ω2

σ + β
3 3
; Ω2 = K 2 α − 4πGρβ
2 2

Ω2 = K 2 C2 − 4πGρ ; V = H

; F = 1 + c K
j 2
4πρ
ωpe
(19)
The determinant of the matrix of (19) gives the dispersion relation
K V {
2 }

σ σξ + ξ
K 2 V2
[ξ
σξ3 + ξ2
] F
σξ3 + ξ2ΩT
= 0

3 2
F
Ω2 2 2

− T ξ2 K 2 K V
K 2
2 x F
(20)
Eq(20) represents the dispersion relation for an infinite homogeneous, thermally conducting, radiating and self- gravitating gas particle medium in the presence of fine-dust-particles, having uniform magnetic field in z- direction. If we neglect the effect of thermal conductivity and radiative term in eq.(20), we get the result as obtained by SHARMA10 and that of CHHAJLANI13 et.. al neglecting the contribution of electrical conductivity.
4. Discussion:-
It is convenient to discuss this dispersion relation for longitudinal and transverse propagation separately.
4.1 Longitudianal propagation:-
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1145
ISSN 2229-5518
We assume the perturbation in parallel direction to magnetic field (K x = 0, K z = K ) . The dispersion relation
(20) is reduced to
σ σ ξ +ξ
2
K 2 V2
ξ
] σ ξ +ξ Ω2 = 0

3 2 3
F
3 2 T
(21)
Resubstituting the values of ξ2 , ξ3 and T
we get of twelfth degree equation in the terms of σ . This equation
splits into four factors represting different modes due to various effect discussed below;
The first factor of Equation (21) gives us
σ= 0
(22)
Which is neutrally stable mode.
This second factor of Eqn.(21) gives the cubic equation
KNτ 4 4 K 2 V2 K 2 V2
τσ3 + 1 + + υK 2 τ σ2 + υK 2 + τ σ + = 0





ρ 3
3
F F
(23)
This dispersion relation show the combined influence of magnetic field, viscosity, finite electron inertia and fine-dust-particles on the self gravitational instability of the gaseous plasma. This mode does not depend on self-gravitation thermal conductivity and heat-loss function. But this is a stable mode as the last term is constant with positive sign, and Eq, (4.3) can never have a negative real root or a complex root whose real part is not positive values.This necessary for stability of the system and is satisfied. The sufficient condition is that the Routh-Hurwitz criterion must be satisfied, according to which all the principal diagonal minors of the Hurwitz
matrix must be positive for a stable system and we get
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1146
ISSN 2229-5518
∆ = τ 1 + KNτ + 4 υK 2 τ 〉 0


I ρ 3
4 KNτ 4 4 K 2 V2
∆ = υK 2 + + υK 2 τ υK 2 + τ 〉 0





2 3 ρ 3
3 F
K 2 V2

∆3 = ∆2 〉 0
F
We find that all ∆ ’s are positive so we find that a magnetized, viscous gas particle medium is stable even in the presence of fine-dust-particles.
The third factor of Equation (21) gives us a quadratic equation
τσ2 + 1 + KNτ + υK 2 τ σ + υK 2 = 0

ρ
(24)
Which is identical to equation (17) of Sharma (1977) and (16) of Chhajlani et. al(1978). This mode is independent of thermal conductivity, heat-loss function, self-gravitation and magnetic field. According to the necessary and the sufficient condition, equation (24) has all the roots with negative real parts, giving stable mode.
The last factor of Equation (21) gives
τσ4 + [ξ
+ τβ]σ3 + ξ β + 4 υK 2 + τΩ2 σ2 + Ω2 + τΩ2 + β. 4 υK 2 σ + Ω2 = 0


1 1 3
j j I 3 I
(25)
This dispersion relation shows the combined effect of viscosity, thermal conductivity, fine-dust-particles and radiative heat loss-functions on the self Gravitational instability of gaseous plasma. This mode is independent of magnetic field.
We can also discuss the dispersion relation of eqn. (25) in non-dimensional form in terms of self gravitatation and we can draw a curve of the non-dimensional growth rate verses non-dimensional wave number k* for various value of thermal conductivity and density dependent radiative heat-loss function.

The variation of non-dimensional growth rate verses non-dimensional wave number k*are shown in fig. (1-2)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1147
ISSN 2229-5518
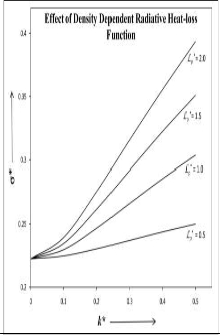
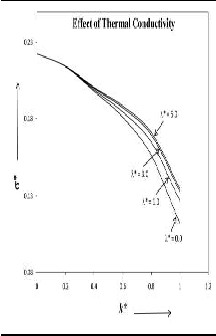
Fig. 1 Fig. 2
In fig. 1 we have depicted the non-dimensional growth rate verse non-dimensional wave number k* variation in
the normalized thermal conductivity effectλ ∗ = 0.0, 1.0, 3.0, 5.0 and the value of other parameter are fixed.
From fig. 1 we observe that the growth rate is minimum for non thermally conducting medium while the higher
values of thermal conductivity increased the instability growth rate. In other words we can say that the thermal conductivity has destabilizing influence on the system.
In fig. 2 wave number k* with variation in the normalized density dependent heat-loss function ℒ𝜌∗ = 0.5, 1.0,
1.5, 2.0. and the value of other parameter are fixed .
From fig. 2 we analyze that the density dependent heat-loss function plays a same role as thermal conductivity and electrical resistivity play to destabilize the system. It means that the increasing values of density dependent heat-loss function increases the growth rate of instability.
Now we can say that eqn. (25) may be reduced to particular cases so that the effect of each factor may be discussed separately.
For only self-gravitating viscous gas particle medium in the presence of fine-dust-particles, we have
2
ΩI = 0,β = 0 and equation (4.5) is reduced to

τσ3 + [ξ ]σ2 + 4 υK 2 + τ Ω2 σ + Ω2 = 0

1 3
j j
(26)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1148
ISSN 2229-5518
This is a third degree equation and it is identical to Eqn. (16) of Sharma (1975) and the condition of instability
obtained from Eq. (26) from constant term is K<Kj where Kj is the critical Jeans wave number given as
K j =
4πGρ
C2

(27)
And corresponding critical Jeans wave length is
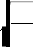
π λ j = C Gρ
(28)
The system is unstable for all Jeans length λ > λ j or wave numbers K<Kj thus we find that Jeans criterion of instability holds good in the presence of fine-dust-particles on the gravitational instability of an infinite
homogeneous gas-particle medium.
It is observed from Dispersion relation Eq.(23),being have two parts. The terms by multiplying
C2 K 2

2 pe
appeared
due to our consideration of finite electron inertia parameter in the present problem. Thus we find that electron inertia has a major role on the various modes of dispersion relation. Hence electron inertia is important in the problems of magnetic reconnection processes stability of an accelerated plasma and in the plasma confinement problems.
For viscous, non-radiating, but thermally conducting self-gravitating gas particle medium in the presence of fine-dust-particles, equation (25) becomes
τσ4 + [ξ
+ τΩ
]σ3 + ξ Ω
+ 4 υK 2 + τΩ2 σ2 + Ω2 + τΩ Ω2 + Ω . 4 υK 2 σ


1 K 1 K 3
j
j K jI K 3
+Ω .Ω2 = 0
(29)
Where

Ω . = γλK
; Ω2
= C`2 − 4πGρ
K ρC jI
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1149
ISSN 2229-5518
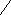
1

C′ = p
ρ
is the isothermal velocity of sound.
Equation (29) represents the dispersion relation showing the effect of viscosity and thermal conductivity on the gravitational instability of an infinite homogeneous gas particle medium in the presence of fine-dust-particles. This is fourth degree equation and the condition of instability obtained from equation (4.9) from constant term
is K< Kj1, where Kj1 is the modified critical jeans wave number, given as
K j1 =
4πGρ
C′2

(30)
And corresponding critical Jeans wave length is
λ j1
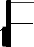
= C′ π
Gρ
(31)
On comparing Eq. (27) and (30), it is obvious that due to thermal conduction, the sonic velocity is altered form adiabatic to isothermal one in Jeans expression. Also comparing (28) and (31) we have
1
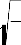
λ j1 = λ j γ
(32)
Since λ > 1,C > C′ therefore owing to thermal conduction. Jeans length is reduced. Thus the thermal conduction destabilizes the system.
If we consider viscous, self-gravitating radiating and thermally non conducting gas particle medium in the presence of fine-dust-particles, then Eq. (25) will reduce to
τσ4 + [ξ
+ τβ
]σ3 + ξ β
+ 4 υK 2 + τΩ2 σ2 + Ω2 + τΩ2 + β
4 υK 2 σ + .Ω2 = 0

1 0 1 0 3
j

j I0 0 3 I0
(33)
Where
α0 = (γ −1)(L T
T − ρL ρ

) ; β = (γ −1)L T Tρ
0 p
and
Ω2 =
K 2α − 4πGρβ
I0 0 0
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1150
ISSN 2229-5518
Evidently, if
Ω2 < 0 the above equation will possess at least one real positive root implying there-by instability
of the system. Thus we find that the system is unstable for all the wave number K such that K<Kj2

1 2

Where
K = K
γL T
j2 j
L T −
ρ L T T
(34)
It is clear from Equation (34) that in this case the critical Jeans wave number depends on the derivatives of the
heat-loss function with respect to local temperature and density in the configuration. The critical Jeans wave
number vanishes if the heat-loss function is independent of temperature (L T = 0) andγ
times of original
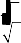
critical Jeans wave number if the heat-loss function is purely temperature-dependent (L T = 0) it may be remarked that the critical wave number decreases or increases as the heat-loss function respectively increases or decreases with increases in density.
Owing to simultaneous effect of all the parameters represented by the original dispersion relation (25), the
condition of instability obtained from (25) form constant term is
Equation (25) will remain unstable for all the wave number K<Kj3
Ω2 < 0 , therefore the system represented by
Where
K 2 = =1 a ±

(a 2 + b )
j3 2
1 I 1
4πGρ

1 2
ρ2L

ρ − ρL T
And
C′λT λ
b1 =
16πGρ2

λC′2 L T
(35)
It is observed, from Eq.(35) that the critical number Kj3 is very much different from the classical Jeans value Kj and depends upon the thermal conductivity and the derivatives of the heat-loss function with respect to local temperature and density in the configuration. It can be easily worked out that for a purely density-dependent
heat-loss function [L T = 0] , the critical wave number is increased or decreased depending on whether the heat-
loss function is an increasing or decreasing function of the density. Furthermore, it can be seen that for a purely
temperature-dependent heat-loss function (L T = 0)
(35) suggests a monotonic instability if K<Kj1 .
which increase with temperature (L T
〉 0)
the condition
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1151
ISSN 2229-5518
However, if instead, the heat-loss function decreases with temperature (L T
〈 0)
the modified Jeans critical
wave number lies between the values of

L T and
λ
4πGρ

C′2
We now discuss the dynamical stability of the system by applying the Routh-Hurwitz criterion to Eq. (25). If
2
ΩI 〉 0 then all the coefficients in Eq. (25) are positive and satisfying the necessary condition for the stability.
To achieve the sufficient condition, the Routh-Hurwitz criterion must be satisfied, according to which all the principal diagonal minors of the Hurwitz matrix must be positive for a stable system.
For Eq. (25) the four principal diagonal minors of Hurwitz matrix are all positive as shown here under
Δ1 = τ (ξ1 + τβ ) > 0
4 2 2 KN 4 2 2 2 2



Δ = ξ ξ β + υK + τ τΩ + υK + ξ β + τ K γ −1 L ρ > 0,
2 ρ 1 1 3ρ
j 1
3
Kγ2 ( 1−
)L.ρ ξ
2τ+Ω3 2τ+β 2 4
2τ+ξ β τ+Ω2 2

ρ 1 1 υK
3
1 j
KNτ 4 4



Δ = + + υK2 τ .τ. β υK2Ω2 + τΩ2Ω2 + βξ Ω2 + τβ2Ω2 + ξ
4 υK2 {ξ β2 + Ω2 } + > 0
3 ρ 3
3

j j I 1 I I I 3
I j
ξ .β
4 υK2
4 υK2 +τβ2
+ ξ . 4 υK2 τΩ2 + τ2β2Ω2
4 υK2

1 3

3

1 3

I j 3
since γ > 0
Δ = Ω2 .Δ > 0
Therefore the system represented by (25) will remain stable if
Ω2 . =
(K 2α − 4πGρβ ) > 0
Thus we find that for longitudinal wave propagation the gravitating plasma is stable if the condition
Kα2
−4πGρβ
is satisfied .
4. 2 Transverse propagation:-
We assume the perturbations in perpendicular direction to magnetic field
[i.e.K x = K and K z = 0] . The dispersion relation (21) is reduced to
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1152
ISSN 2229-5518
σ3 .ξ 2 . σξ 2 + σξ ξ Ω2 + ξ ξ
K 2 V2

= 0
3 3 2 3 T 2 3
F
(36)
Resubstituting the values of ξ2 ,ξ3
and
2 we get twelfth degree equation in term of σ . This equation splits
into three factors representing different modes due to various effects as discussed below.
The first factor of Equation (36) gives us
σ = 0
(37)
This is same as discussed in Eqn.(4.2) and representing stable mode.
The second factor of Eqation (36) gives us:
τσ2 + 1 + 4 υK 2 τ + KN τ σ + υK 2 = 0


3ρ
(38)
This is same as discussed in Equation (24) and representing again stable mode.
The third factor of Equation (36) gives us
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1153
ISSN 2229-5518
τ2σ6
τ2β 2τξ σ5
2τξ β ξ2
τ τΩ2
τ V K 6 υK2 σ4
+ +


+ + + + +
1
1 I j F 3
+ ξ 8 υK2 + τΩ2 + τ V K
V K

+ τ Ω2 +
V K

+ τ2 Ω2 +
2 8 2 3

β + β ξ + υK τ σ
2 2 2 2 2 2


3
F
F F
I 3
4 2 2 4 2 4 2 V K




υK τΩ − υK + υK
V K

τ + ξ
+ Ω2
2 2 2 2
1
F
j
2
+β
8 υK2ξ
+ τξ
V K + τ V K
+ Ω2 ( τ + τξ )

3


1 I F F I I
2 2
2
2 2 2 2
+ 4 υK2
Ω2 + V K + β
4 υK2
+ 4 υK2 V K
τ + ξ V K
+ Ω2
4 υK2 τ + ξ
σ +


3 j F



3 3

F 1 F

I 3 1
4 2 2 V K


υK Ω + β = 0
3
F
(39)
This dispersion relation represents the effect of simultaneous inclusion of the viscosity, finite electron inertia, thermal conductivity and heat-loss function on the magneto gravitational instability of a infinite homogeneous self-gravitating gas particle medium in the presence of the fine-dust-particles, when disturbances are propagating perpendicular to the direction of the magnetic field. The condition for the constant term of Equation
(4.19) is

Ω2 + β V K < 0
I F
(40)
Therefore the system represented by Eq. (39) will remain unstable for all the wave number K<Kj4
Where
K 2 = =1 a ±

a 2 + b
j4 2
2 2 2
4πGρ

a +
ρ2L
ρ

1 +
−1
V2


− L Tρ ; b
16πGρ2 L

=
T 1 +
−1
V2

2 C′λ2T
C F
′2 λ C2
λ′2
C F
′2
(41) It may be remarked here that
the critical wave number depends upon the strength of magnetic field, thermal conductivity and derivative of general heat-loss function as temperature dependent and density-dependent configuration. It is obvious that the magnetized field decreases the Jeans wave number. Thus the magnetized field stabilizes the medium for
traverse propagation.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1154
ISSN 2229-5518
V2 K 2
When, Ω2 + β > 0
equation (39) has all the coefficient positive. Hence according to Hurwitz’s

I
necessary condition the system is stable; but this is not a sufficient condition for stability.
5. Conclusions:-
We have analyzed an infinite homogeneous self-gravitating, viscous and magnetized gas particle medium with thermal conductivity and radiative effects in the presence of fine-dust-particles with finite electron inertia. To sum up the results we may conclude that in all the cases considered the Jeans instability condition remains valid. Viscosity and fine-dust-particles have dissipative effect but do not affect the jeans expression. Thermal conduction affects the sonic speed appearing in Jeans expression in replacing adiabatic term by isothermal one. For longitudinal propagation the condition of radiative instability and critical Jeans wave number respect to local temperature and density in the configuration but do not depend on the magnetic field. But in transverse direction, it is found that the condition of radiative instability and critical jeans wave number depend on magnetic field along with thermal conductivity and the derivatives of the heat-loss function with respect to local temperature and density in the configuration. It is also seen that viscosity and fine-dust-particles do not affect the condition of radiative instability.
REFERENCES:-
[1] J. H. Jeans, Phil. Trans. Roy. Soc. London , A199(1902), 1.
[2] S.Chandrasekhar, Hydrodynamic and hydromagnetic Stability, Clarendon Press, Oxford., 1961 [3] J. H. Jeans, Astronomy and Cosmogony, Cambridge Uni. Press, Camgridge (1929)313.
[4] R.C. Sharma,suspended particles and the Gravitational Instability, Zeit Apple. Math. Mech. 55 (1975)
615-616.
[5] W.D.Langer, The Stability of Interstellar Clouds Containing Magnetic fields,Astrophysical Journal,225 (1978) 95-106
[6] L. Mestel and L. Spitzer, Star formation in magnetic dust clouds, Monthly Notices Roy. Astron. Soc.,
116(1956) 503.
[7] L. Spitzer, Physics of Fully Ionized Gases, New York (Interscience),(1962). [8] L Spitzer, Diffuse Matter in space, New York (Interscience),(1968).
[9] R. C. Sharma, Effect of Magnetic Field on the Gravitational Instability of Self Gravitating Homogeneous
Gas Particle Medium in the Presence of Suspended Particles, Astrophyics Space Sc., 46(1977) 225.
[10] R.C. Sharma and K.C. Sharma, Suspended particles and the gravitational instability of a rotating plasma, Astrophysics Space Sc., 71(1980)325.
[11] K.C. Sharma, Gravitational instability of a Hall plasma in the presence of suspended
particles,Astrophysics Space Sc., 85(1982)263.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1155
ISSN 2229-5518
[12] R. K. Chhajlani, P. Vashistha, And S. C. Bhand, Effect of Conductivity on Magneto-Gravitational
Instability and Suspended Particles, Z. Naturforsch, 339(1978)1469.
[13] R. K. Chhajlani and P. Purohit, The Effect of Finite Larmor Radius on Gravitational Instability of a
Finitely Conducting Magnetised Hall Medium in Presence of Suspended Particles, Beiter Plasma Phys.,
24(1984)3.
[14] G. B. Field, Thermal Instability, Astrophysics J., 142(1965) 265.
[15] M.K.Vyas and R.K. Chhajlani, Magnetogravitational instability of an infinite homogeneous rotating plasma through a porous medium with finite electrical and thermal conductivities, Astrophysics Space Sc.,
140(1987) 89.
[16] R. K. Chhajlani and D. S. Vaghela, Magnetogravitational stability of self-gravitating plasma with thermal conduction and finite Larmor radius through porous medium, Astrophysics Space Sc., 134(1987)301.
[17] S. Vaghela and R. K. Chhajlani, Gravitational Instability of Fluid of Finite Electrical and Thermal
Conductivity Flowing through Porous Medium, Contrib. Plasma Phys., 27(1987)3.
[18] S. Vaghela, and R. K Chhajlani, Magnetogravitational Stability of Resistive Plasma through Porous
Medium with Thermal Conduction and FLR Corrections, Contrib. Plasma Phys., 29(1989)1
[19] R. K. Chhajlani and A. K. Parihar, Stability of Self-Gravitating Magnetized Hall Plasma with Electrical and Thermal Conductivity through Porous Medium, Contrib. Plasma Phys., 33(1993) 3.
[20] Ali and P. K. Bhatia, Gravitational instability of a thermally conducting viscous Hall plasma, Physica
Scripta, 47(1993) 561.
[21] M. Aggarwal and S. P. Talwar, Monthly Notices Roy. Astron. Soc., 146(1969)235.
[22] M. Aggrawal and S.P Talwar, Contrastreaming Instability in Gravitating Fluids with Thermal Effects, Publ. Astron. Soc . Japan., 21(1969)176.
[23] M. P. Bora and S. P. Talwar, Magnetothermal instability with generalized Ohm's law,Phys. Fluids
B5(3)(1993)950.
[24] S.P. Talwar and M. P. Bora, Thermal instability in a star—gas system, J. Plasma Physics. 54(1995)157. [25] R. K. Chhajlani and D. S. Vaghela, Gravitational stability of finitely conducting two-component plasma
through porous medium, Astrophysics and space Science, 139(1987)337.
[26] R.K. Pensia, V. Ghorela and R.K. Chhajlani, Magneto –Thermal Instability of self gravitating Viscous
Hall Plasma in the Presence of Suspended Particles.,Acta Ciencia Indica,ΧΧΧV,2(2009)141.
[27] R.K. Pensia, V. Kumar, V. prajapat,Role of Magnetic field in contraction and fragmentation of
Interstellar clouds,Ultrascientist ,22(2010),2,pp-253.
IJSER © 2014 http://www.ijser.org


